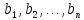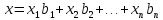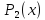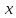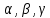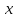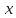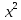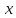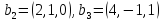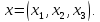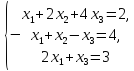Как найти базис системы вектор столбцов

Как найти базис системы вектор-столбцов

Перед рассмотрением данного вопроса стоит напомнить, что любая упорядоченная система n линейно независимых векторов пространства R^n называется базисом этого пространства. При этом образующие систему векторы будут считаться линейно независимыми, если любая их нулевая линейная комбинация возможна только за счет равенства нулю всех коэффициентов этой комбинации.

Вам понадобится

• – бумага;
• – ручка.

Инструкция

Пользуясь только лишь основными определениями проверить линейную независимость системы вектор-столбцов, а соответственно и дать заключение о наличии базиса, весьма затруднительно. Поэтому в данном случае вам может помочь использование некоторых специальных признаков.

Известно, что векторы линейно независимы, если составленный из них определитель не равен нулю.Исходя из этого, можно достаточно объяснить тот факт, что система векторов образует базис. Итак, для того чтобы обосновать, что векторы образуют базис, следует составить из их координат определитель и убедиться, что он не равен нулю.В дальнейшем, для сокращения и упрощения записей, представление вектор-столбца матрицей-столбцом будем заменять транспонированной матрицей-строкой.

Пример 1. Образуют ли базис в R^3 вектор-столбцы (1, 3, 5)^T, (2, 6, 4)^T, (3, 9, 0)^T.Решение. Составьте определитель |A|, строками которого являются элементы заданных столбцов (см. рис.1).Раскрыв этот определитель по правилу треугольников, получится: |A| = 0+90+36-90-36-0=0. Следовательно, эти векторы не могут образовать базис.

Пример. 2. Система векторов состоит из (10, 3, 6)^T, (1, 3, 4)^T, (3, 9, 2)^T. Могут ли они образовать базис?Решение. По аналогии с первым примером составьте определитель (см. рис.2): |A| =60+54+36-54-360-6=270, т.е. не равно нулю. Следовательно, эта система вектор-столбцов пригодна для использования в качестве базиса в R^3.

Теперь со всей очевидностью становится ясно, что для нахождения базиса системы вектор-столбцов вполне достаточно взять любой определитель подходящей размерности отличный от нуля. Элементы его столбцов образуют базисную систему. Мало того, всегда желательно иметь простейший базис. Так как определитель единичной матрицы всегда отличен от нуля (при любой размерности), то в качестве базиса всегда можно выбрать систему (1, 0, 0,…,0)^T, (0, 1, 0,…,0)^T, (0, 0, 1,…,0)^T,…, (0, 0, 0,…,1)^T.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Как найти координаты вектора в базисе

Решение:
Записываем матрицу перехода А:

и находим ее определитель
<>0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f₁ , f₂ , f₃ линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:

Обратная матрица А -1

Находим координаты вектора х относительно нового базиса.

Пример №1 . Даны векторы a<1;2;1>, b<2;-2;1>, c <1;-2;0>и d <0;3;1>. Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 – β*2 – γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b – 3/2c

Пример №2 . Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе:

Пример №3 . Даны два линейных преобразования:
х’₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃, х”₁ = b₁₁x’₁ + b₁₂x’₂ + b₁₃x’₃,
х’₂ = a21x1 + a22x2 + a23x3, х”₂ = b₂₁x’1 + b₂₂x’₂ + b₂₃x’₃,
х’₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃, х”₃ = b₃₁x’₁ + b₃₂x’₂ + b₃₃x’₃,
Средствами матричного исчисления найти преобразование, выражающее х”₁, x”₂, x”₃ через х₁, х₂, х₃.
х’₁ = 4x₁ + 3x₂ + 5x₃, х”₁ = – x’₁ + 3x’₂ – 2x’₃,
х’₂ = 6x₁ + 7x₂ + x₃, х”₂ = – 4x’₁ + x’₂ + 2x’₃,
х’₃ = 9x₁ + x₂ + 8x₃, х”₃ = 3x’₁ – 4x’₂ + 5x’₃,
Решение. Используя калькулятор, получаем:
Обозначим:

Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 – 1*1) – 6*(3*8 – 1*5) + 9*(3*1 – 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .

A -1 = -1/182

55 -19 -32 -39 -13 26 -57 23 10

Матрицу Х ищем по формуле:

X = A -1 ·B = -1/182

55 -19 -32 -39 -13 26 -57 23 10

*

=

75 /182 -1 46 /91 1 9 /13 -13 /14 1 2 /7 -1 5 /182 1 3 /91 -1 2 /13

Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e ₁= AB , e ₂= AC , e ₃= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e ₁, e ₂, e ₃)

Решение. Пункты (а-д) решаются через онлайн калькулятор.

Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид
Решим полученную систему уравнений.

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 – 2 1 – 1 1 2 – 2 A = 3 – 2 1 2 1 2 3 – 1 – 2 = 3 · 1 · ( – 2 ) + ( – 2 ) · 2 · 3 + 1 · 2 · ( – 1 ) – 1 · 1 · 3 – ( – 2 ) · 2 · ( – 2 ) – 3 · 2 · ( – 1 ) = = – 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , – 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , – 1 , – 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 – 1 1 0 1 – 2 1

1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 – 2 – 1

1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , – 1 , – 2 ) a ( 2 ) = ( 0 , 2 , 1 , – 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства – e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n – некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 – x 1 ) · e ( 1 ) + ( x

2 – x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 – x 2 ) , . . . , ( x

n – x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , – 1 , 1 ) e ( 2 ) = ( 3 , 2 , – 5 ) e ( 3 ) = ( 2 , 1 , – 3 ) x = ( 6 , 2 , – 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 – 1 1 3 2 – 5 2 1 – 3

1 – 1 1 0 5 – 8 0 3 – 5

1 – 1 1 0 5 – 8 0 0 – 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 – 1 2 1 1 – 5 – 3 = – 1 ∆ x

1 = 6 3 2 2 2 1 – 7 – 5 – 3 = – 1 , x

1 ∆ = – 1 – 1 = 1 ∆ x

2 = 1 6 2 – 1 2 1 1 – 7 – 3 = – 1 , x

2 ∆ = – 1 – 1 = 1 ∆ x

3 = 1 3 6 – 1 2 2 1 – 5 – 7 = – 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) – координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

Базис системы вектор столбцов

Ну вот, смотрите:
Три первых столбца — базис.
Четвертый мы по нему раскладываем.
Обозначим базисные столбцы через е1, е2, е3.
Чтобы первый элемент четвертого столбца был равен -3, нам нужно взять е1 и умножить его на -3.
Получим вектор:
-3
0
0
0

Чтобы получить второй элемент, равный 6, надо к -3е1 прибавить 6е2. Получим:
-3
6
0
0

У каждого базисного вектора единица только в одном месте. Она отвечает за одну координату; другие при сложении не портятся.
В итоге должны получиться выражения для е4, е5 как линейные комбинации первых трех векторов:
е4=.
е5=.

Попробую объяснить немного с другой стороны.

В данном случае вы фактически решили систему линейных уравнений с ТРЕМЯ неизвестными и ДВУМЯ правыми частями методом Гаусса. Матрица системы это три первых столбца. Остальные два столбца это правые части. Если несколько правых частей для вас непривычная конструкция, считайте, что это несколько систем с одной и той же матрицей системы, но с разными правыми частями. Решение системы это три числа. Они должны быть такими, что умножая первые три столбца на эти три числа и складывая мы получим правую часть. То есть это коэффициенты линейной комбинации первых трех столбцов, которая равна правой части. Таким образом любую правую часть можно выразить через первые три столбца. С другой стороны эти столбцы линейно независимы. В самом деле, если предполжить, что их линейная комбинация равна нулю (правая часть системы равна нулю), то вы получите нулевое решение, то есть линейная комбинация тривиальна. Ну а полная и линейно независимая система столбцов и есть базис.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/vektory/vektornoe-prostranstvo/

http://diary.ru/~eek/p130236068_bazis-sistemy-vektor-stolbcov.htm

[/spoiler]

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

В
линейном
пространстве наибольший
интерес представляют системы
векторов, в
виде линейной
комбинации которых
можно представить любой вектор, причем
единственным образом. Если зафиксировать
такую систему векторов, то любой вектор
можно будет однозначно представить
набором чисел, являющихся коэффициентами
соответствующей
линейной
комбинации, а
всевозможные векторные соотношения
превратить в соотношения числовые.

Этот
подход применялся уже в аналитической
геометрии. В пространстве
векторов на плоскости любые два
неколлинеарных вектора образуют базис,
так как через такую пару векторов любой
вектор плоскости выражается однозначно
в виде линейной комбинации. Аналогично
в(множестве векторов в пространстве)
базис образуют любые три некомпланарных
вектора. Для матриц использовалось
понятие базисных строк и базисных
столбцов. По теореме о базисном миноре
базисные строки (столбцы) линейно
независимы, а любая строка (столбец)
матрицы является линейной комбинацией
базисных строк (столбцов).

Определение
1.3. Базисом
линейного пространства
называют
любую упорядоченную систему векторов,
для которой выполнены два условия:

1) эта
система
векторов линейно независима,

2) каждый
вектор в линейном пространстве может
быть представлен в виде линейной
комбинации векторов этой системы.

Пусть

—
базис в
.
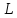
Определение 1.3 говорит о том, что любой
векторможет быть записан следующим образом:

Такую
запись называют разложением
вектора х
по
базису
.

Данное
нами определение базиса согласовывается
с понятием базиса в пространстве
свободных
векторов в
,
или
.
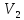
Например, вбазисом была названа любая тройка
некомпланарных векторов. Такая тройка
векторов является линейно независимой,
так как представление одного ее вектора
в виде линейной комбинации двух других
равносильна компланарности трех
векторов. Но, кроме того, из курса
векторной алгебры мы знаем, что любой
вектор в пространстве можно выразить
через произвольные три некомпланараных
вектора в виде
их
линейной
комбинации. Три компланарных вектора
не могут быть базисом в
,
так как любая линейная комбинация таких
векторов даст вектор, им компланарный.

Теорема
1.2 (о единственности разложения). В
линейном пространстве разложение любого
вектора по данному базису единственно.

Выберем
в линейном пространстве

произвольный
базис

и
предположим, что вектор х
имеет
в этом базисе два разложения

Воспользуемся
тем, что аксиомы
линейного пространства позволяют
преобразовывать линейные комбинации
так же, как и обычные алгебраические
выражения. Вычитая записанные равенства
почленно, получим

Так
как базис – это линейно независимая
система векторов, ее линейная комбинация
равна 0,
лишь,
если она тривиальная
(см.
определение 1.2). Значит, все коэффициенты
этой линейной комбинации равны нулю:
.
Таким образом,и
два разложения векторах
в
базисе
совпадают.

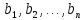
Замечание
1.3. Условие
линейной независимости векторов базиса
означает, что нулевой
вектор имеет
в этом базисе единственное разложение,
а именно тривиальное: все коэффициенты
этого разложения равны нулю. Из
доказательства теоремы 1.2 следует, что
из единственности разложения нулевого
вектора по данной системе векторов
вытекает единственность разложения
любого другого вектора.

Согласно
определению 1.3, базис является упорядоченной
системой векторов. Это значит, что,
изменив порядок векторов в системе, мы
получим другой базис. Порядок векторов
в базисе фиксируют для того, чтобы задать
определенный порядок коэффициентов
разложения произвольного вектора. Это
позволяет заменить линейную комбинацию,
представляющую вектор, упорядоченным
набором ее коэффициентов и тем самым
упростить запись. Порядок векторов в
базисе определяется их нумерацией.

Определение
1.4. Коэффициенты
разложения вектора по базису линейного
пространства, записанные в соответствии
с порядком векторов в базисе, называют
координатами
вектора в этом
базисе.

Пример
1.8. В
линейном пространстве

многочленов
переменного

степени
не выше 2 (см. пример 1.1) элементы

и
линейно
независимы: их линейная комбинация
есть многочлен, который равен нулю
(нулевому многочлену) лишь при.
В то же время пара этих элементов не
образует базиса. Действительно, многочлен
1 нулевой степени, являющийся элементом,
нельзя
представить в виде линейной комбинации
многочленов

и
.Дело
в том, что линейная комбинация

многочленов

и
есть
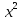
либо многочлен второй степени (при
),
либо многочлен первой степени(,
),
либо нулевой многочлен().
Значит, равенство

двух
многочленов невозможно ни при каких
значениях коэффициентов.

В
то же время три многочлена 1,

и
образуют
базис линейного пространства
.
Докажем это.

Во-первых,
система многочленов 1,

и
линейно
независима. Составим их линейную
комбинацию с произвольными коэффициентами

и
приравняем нулю:
.
Это равенство есть равенство двух
многочленов, и оно возможно только в
случае, когда коэффициенты этих двух
многочленов совпадают. Значит,.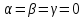

Во-вторых,
через многочлены 1,

и

можно
выразить любой многочлен второй степени,
т.е. любой элемент линейного пространства

можно
представить в виде линейной комбинации
указанных трех элементов.

Итак,
система трех многочленов 1,

и

линейно
независима, а любой элемент линейного
пространства


является
линейной комбинацией указанной системы.
Согласно определению 1.3, система
многочленов 1,

и

есть
базис в
.

Пример
1.10.
В
линейном
арифметическом пространстве
векторы

образуют
базис
,
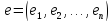
так как они линейно независимы (см.
пример 1.5) и любой вектор
представим
в виде

Такой
базис (1.5) в пространстве
называютстандартным.
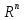
Отметим,
что запись элементов арифметического
пространства в виде столбца не противоречит
определению арифметического пространства,
понимаемого как множество упорядоченных
совокупностей чисел. Порядок же элементов
можно указывать как при помощи записи
в строку, так и при помощи записи в
столбец.

Пример
1.11.
Покажем,
что в
система векторов

образует
базис и найдем в этом базисе координаты
вектора

Для
того чтобы доказать, что система векторов
,,

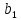
образует базис, надо убедиться в линейной
независимости этих векторов и в том,
что любой вектор
является их линейной комбинацией.

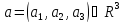
В
стандартном базисе е в
векторыимеют следующие столбцы координат:

Из
стобцов координат векторов
составим матрицу

и
рассмотрим квадратную систему линейных
алгебраических уравнений (СЛАУ)
,Так как,
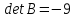
то матрицаневырожденная, ее ранг равен 3 и все ее
столбцы являются базисными. Поэтому,
во-первых, согласно теореме о базисном
миноре, эти столбцы линейно независимы,
значит, СЛАУ
при
любом столбце

правых
частей имеет решение

В
частности, решив СЛАУ
,
которая в координатной форме имеет вид

находим
координаты вектора
в базисе:

.

Соседние файлы в папке Геометрия

• #
• #
• #

ilya_56
Насколько я понял, в Вашем случае имеется пять четырёхкоординатных вектор-столбцов. Сами столбцы записаны в столбцах указанной Вами матрицы, а их одноимённые координаты – в строках этой матрицы.

В качестве базисных можно взять любой набор линейно независимых столбцов, через которые выражаются все остальные столбцы системы. Возьмём в качестве первого базисного первый столбец (1, 1, 2, 2). Второй столбец (2, 1, 1, 1) линейно независим с первым, поэтому его можно взять в качестве второго базисного). Третий столбец (2, 0, 2, 1) линейно независим с первыми двумя, поэтому его можно взять в качестве третьего базисного. И наконец, четвёртый столбец (1, 1, 1, 2) линейно независим с тремя предыдущими, поэтому его можно взять в качестве четвёртого базисного.

Чтобы выразить пятый столбец (3, 2, 1, 2) через базисные, нужно составить и решить систему четырёх уравнений, выражающих то обстоятельство, что координаты пятого вектор-столбца являются линейной комбинацией одноимённых координат соответствующих координат базисных вектор-столбцов. Получим такую систему:

Вам остаётся только решить эту систему. Найденные Вами коэффициенты a, b, c, d и будут координатами пятого вектор-столбца в базисе первых четырёх вектор-столбцов.