Решение. Очевидно,
что данное линейное преобразование
действует
![]()
,
т.к. умножение матриц
![]()
определено, когда количество столбцов
1-й матрицы равно количеству строк
второго вектора (в нашем случае 4), а
полученная матрица имеет размерность
![]()
(т.к. в матрице A
5 строк).
Совокупность N
векторов x
таких, что Ax=0,
называется ядром
преобразования A.
Совокупность M
векторов вида Ax,
когда x
пробегает все R
(в нашем случае
![]()
)
называется образом
пространства
R
при преобразовании A
(другими
словами образ – множество векторов y,
для которых уравнение Ax=y
имеет хотя бы одно решение).
1) Находим ядро.
Пусть
![]()
– вектор столбец. Решаем систему уравнений

.
Решаем систему
методом Гаусса

.
Переменные
![]()
– базисные, а
![]()
– небазисная.
Находим все
фундаментальные решения. В нашем случае
оно одно: положив
![]()
,
получаем
![]()
– который и будет образовывать базис
ядра (т.к. все вектора вида
![]()
отображаются в 0). Размерность базиса
равна 1.
2) Находим образ.
Пусть
– вектор столбец. Решаем систему уравнений
Ax=y.
Для того, чтобы
вектор
![]()
принадлежал образу, необходимо и
достаточно, чтобы ранг матрицы А, и ранг
расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:
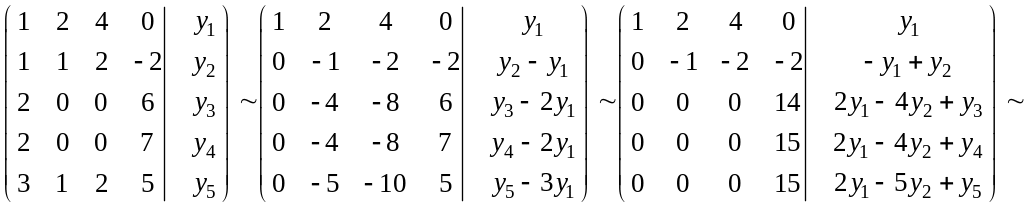

.
Т.к. rang(A)
= 3, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы
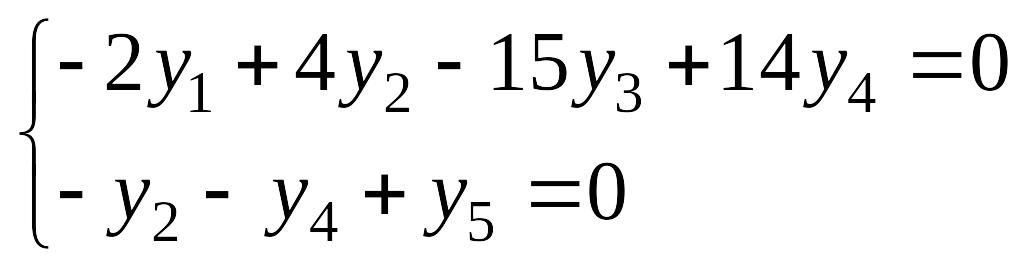
.
Находим фундаментальные
решения (базис образа). Т.к. определитель
из коэффициентов при
![]()
:
![]()
,
то
![]()
– базисные, а
![]()
– небазисные.
1-е фундаментальное
решение. Положим
![]()
,
находим решение системы
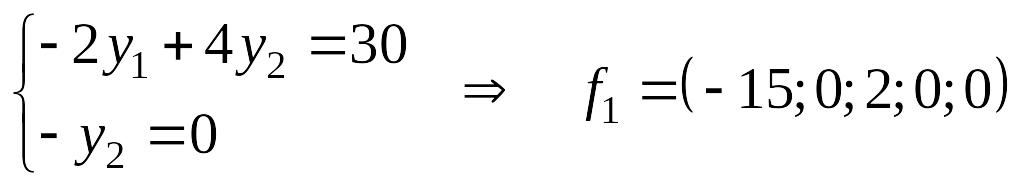
– первое базисное
решение.
2-е фундаментальное
решение. Положим
![]()
,
находим решение системы

– второе базисное
решение.
3-е фундаментальное
решение. Положим
![]()
,
находим решение системы

– второе базисное
решение.
Итак, размерность
образа равна 3, базис – вектора
![]()
.
(Видно, что
размерность образа + размерность ядра
= размерности пространства R4).
7. Найти размерность пространства и , где , а м – пространство решений системы уравнений .
Решение.
![]()
– ядро,
![]()
– образ. Преобразование
![]()
.
1) Находим ядро.
Решаем систему уравнений

Следовательно,
одно базисное решение
![]()
– базис ядра. Размерность
![]()
.
2) Находим образ.
Пусть
![]()
– вектор столбец. Решаем систему уравнений
Ax=y.
Для того, чтобы
вектор
![]()
принадлежал образу, необходимо и
достаточно, чтобы ранг матрицы А, и ранг
расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

.
Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы
![]()
Отсюда,
![]()
–
базисная, а
![]()
не базисные переменные.
1-е фундаментальное
решение:
![]()
.
2-е фундаментальное
решение:
![]()
.
Следовательно,
![]()
– базис образа. Размерность
![]()
.
3) Находим
ортогональное дополнение
![]()
.
Т.к. любой вектор
![]()
,
перпендикулярен любому вектору из
,
то заключаем, что скалярное произведение
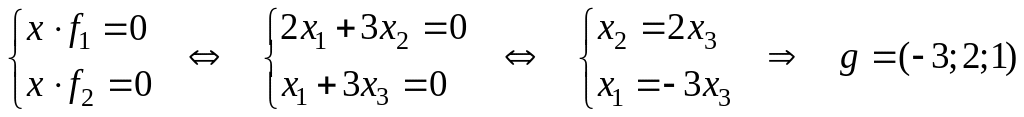
– фундаментальное
решение системы или базис
![]()
.
4) Найдем базис
линейной оболочки векторов
![]()
,
![]()
.
Т.к.

,
то заключаем, что
,
– базис в
,
и следовательно, размерность
![]()
.
5) Находим пространство
решений системы уравнений
.
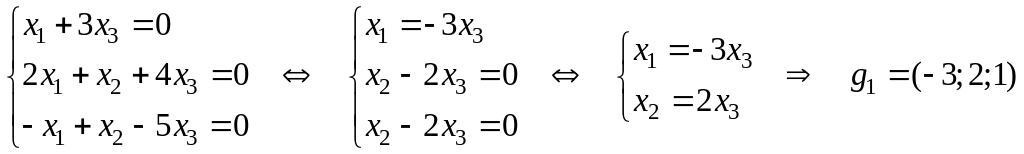
– фундаментальное
решение системы или базис M.
6) Находим
ортогональное дополнение
![]()
.
Т.к. любой вектор
![]()
,
перпендикулярен любому вектору из
![]()
,
то заключаем, что скалярное произведение
![]()
.
Отсюда,
![]()
–
базисная, а
![]()
не базисные переменные.
1-е фундаментальное
решение:
![]()
.
2-е фундаментальное
решение:
![]()
.
Следовательно,
![]()
– базис
.
Размерность
![]()
.
7) Найдем базис
линейной оболочки векторов
,
,
,
.
Очевидно, что
![]()
,
а
,
– базис в
,
и следовательно, размерность
![]()
.
8. Пусть U
– подпространство
линейного пространства R4,
являющееся линейной оболочкой. векторов
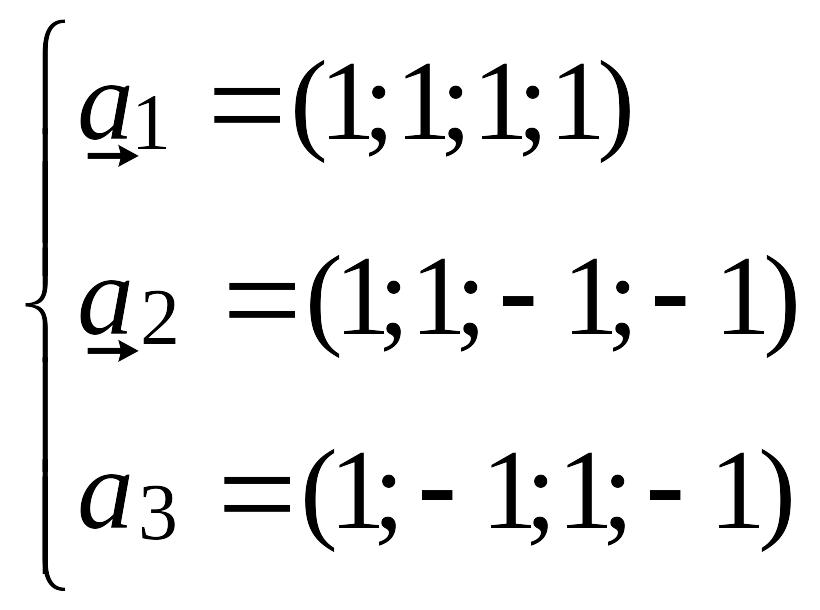
,
V
– подпространство
линейного пространства R4
являющееся
линейной оболочкой векторов

.
Найдите: базис U
+ V
и
базис
![]()
.
Решение.
1) Находим базис в
U.

rang=3
, сл-но,
![]()
– базис U.
1) Находим базис в
V.

rang=3
, сл-но,
![]()
– базис V.
3) Находим базис в
U
+ V.
Находим линейно
независимые вектора в объединении
![]()
.

![]()
,
а вектора
![]()
– базис U
+ V
, а размерность
dim(U
+ V)=4.
4) Найдем общие
вектора в U
и
V
.
Нам известно, что
в конечномерном пространстве
подпространства могут быть заданы
системами линейных уравнений. Тогда их
пересечение задаётся системой уравнений,
полученной объединением систем, задающих
подпространства.
Система уравнений
задающая U:
Для того, чтобы
вектор
принадлежал линейной оболочке U,
необходимо и достаточно, чтобы ранг
матрицы А и ранг расширенной матрицы
(A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

Т.к. rang(A)
= 3, то для того чтобы rang(A|y)
=3, необходимо и достаточно, чтобы
![]()
– искомая система
линейных уравнений.
Система уравнений
задающая V:
Для того, чтобы
вектор
принадлежал линейной оболочке U,
необходимо и достаточно, чтобы ранг
матрицы А и ранг расширенной матрицы
(A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

Т.к.
rang(A)
= 3, то для того чтобы rang(A|y)
=3, необходимо и достаточно, чтобы
![]()
– искомая система
линейных уравнений.
Решаем общую
систему:

.
Отсюда фундаментальные
решения (которые получаются при
![]()
и при
![]()
),
а следовательно базис
есть:
![]()
.
9. Подпространство
L1
в R4
порождено векторами (1;-4;6;7) и (0;1;-3;1), а
подпространство L2
– векторами
(0;1;-4;5) и (1;-4;7;-11). Постройте базисы следующих
подпространств: пересечения
![]()
и ортогонального дополнения к сумме
![]()
.
Решение.
1) Находим базис в
L1.
Т.к. матрица, составленная из координат
векторов
![]()
,
имеет ранг=2 (т.к. в ней есть определитель
второго порядка
![]()
),
то заключаем, что вектора
![]()
=(1;-4;6;7)
и
![]()
=(0;1;-3;1)
линейно независимые и образуют базис
в L1.
2) Аналогично,
заключаем, что вектора
![]()
=(0;1;-4;5)
и
![]()
=(1;-4;7;-11)
линейно независимые и образуют базис
в L2.
3) Находим базис
L1+
L2.
Рассматриваем
объединенную систему векторов
=(1;-4;6;7),
=(0;1;-3;1),
=(0;1;-4;5),
=(1;-4;7;-11)
и находим среди
них линейно независимые. Находим ранг
матрицы, столбцами которой являются
координаты
![]()
:

.
Ранг = 4, следовательно,
все вектора
– линейно независимые и образуют базис
в L1+
L2.
4)
Находим базис ортогонального дополнения
.
Каждый вектор из
![]()
ортогонален любому вектору из L1+
L2.
Следовательно, скалярные произведения
на вектора базиса из L1+
L2
равны 0. Получаем однородную систему
![]()
.
Т.к. определитель
системы не равен 0 (показано выше, что
ранг=4), то система имеет единственное
тривиальное решение
![]()
.
Следовательно,
состоит
только из одного вектора
![]()
.
(Это и так было
видно, т.к. линейная оболочка
![]()
,
ибо 4 линейно независимых вектора
образуют базис в
![]()
,
а
![]()
).
5) Находим систему
уравнений описывающую L1.
Для того, чтобы
вектор
принадлежал линейной оболочке
,
необходимо и достаточно, чтобы ранг
матрицы А – составленной из координат
векторов
,
и ранг расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

.
Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы
![]()
– искомая система
линейных уравнений.
Находим систему
уравнений описывающую L2.
Для того, чтобы
вектор
принадлежал линейной оболочке
,
необходимо и достаточно, чтобы ранг
матрицы А – составленной из координат
векторов
,
и ранг расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

.
Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы
![]()
– искомая система
линейных уравнений.
Решаем общую
систему:
![]()
Т.к. определитель
матрицы коэффициентов
![]()
,
то система имеет единственное решение
![]()
.
Следовательно,
состоит из
одного вектора (0;0;0;0).
(Это и так было
видно, т.к. вектора
– линейно независимые,
линейные оболочки
![]()
и
![]()
не имеют общих (кроме нулевого) векторов,
т.к. линейная комбинация векторов
![]()
не может дать вектора
![]()
,
а следовательно и их линейные комбинации).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ядро и образ линейного отображения
Ядром линейного отображения называется множество таких векторов
, что
, т.е. множество векторов из
, которые отображаются в нулевой вектор пространства
. Ядро отображения
обозначается:
Образом линейного отображения называется множество образов
всех векторов
из
. Образ отображения
обозначается
или
Заметим, что символ следует отличать от
— мнимой части комплексного числа.
Примеры ядер и образов линейных отображений
1. Ядром нулевого отображения является все пространство
, а образом служит один нулевой вектор, т.е.
2. Рассмотрим отображение , которое ставит в соответствие каждому вектору
n-мерного линейного пространства
его координатный столбец
относительно заданного базиса
. Ядром этого отображения является нулевой вектор
пространства
, поскольку только этот вектор имеет нулевой координатный столбец
. Образ преобразования
совпадает со всем пространством
, так как это преобразование сюръективно (любой столбец из
является координатным столбцом некоторого вектора пространства
).
3. Рассмотрим отображение , которое каждому вектору
n-мерного евклидова пространства
ставит в соответствие алгебраическое значение
его проекции на направление, задаваемое единичным вектором
. Ядром этого преобразования является ортогональное дополнение
— множество векторов, ортогональных
. Образом является все множество действительных чисел
.
4. Рассмотрим отображение , которое каждому многочлену степени не выше
ставит в соответствие его производную. Ядром этого отображения является множество
многочленов нулевой степени, а образом — все пространство
.
Свойства ядра и образа линейного отображения
1. Ядро любого линейного отображения является подпространством:
.
В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что
т.е. нулевой вектор отображается в нулевой вектор
. Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент:
. Покажем, что множество
замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:
Следовательно, множество является линейным подпространством пространства
.
2. Образ любого линейного отображения является подпространством:
.
В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если
, то существует вектор
такой, что
. Тогда
, то есть
.
Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.
Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа:
.
3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).
В самом деле, если любой базис пространства
, то
. Поэтому максимальное число линейно независимых векторов системы
(ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы
отображения, т.е. рангу матрицы:
.
4. Линейное отображение инъективно тогда и только тогда, когда
, другими словами, когда дефект отображения равен нулю:
.
Действительно, образом нулевого вектора служит нулевой вектор
. Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор
, иначе два разных вектора имели бы один и тот же образ
. Обратно, при условии
разные векторы
не могут иметь одинаковые образы
, так как в этом случае из равенств
, следует, что ненулевой вектор
(приходим к противоречию).
5. Линейное отображение сюръективно тогда и только тогда, когда
, другими словами, когда ранг отображения равен размерности пространства образов:
.
6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда
и
одновременно.
Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:
(9.3)
Действительно, пусть . Выберем в подпространстве
базис
и дополним его векторами
до базиса
всего пространства
. Покажем, что векторы
образуют базис подпространства
.
Во-первых, , так как образ любого вектора
линейно выражается через векторы
Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:
то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению
. Учитывая, что
, заключаем:
. Получили разложение нулевого вектора по линейно независимой системе
векторов, значит, все коэффициенты
. Поэтому равенство
справедливо только для тривиальной линейной комбинации, т.е. система векторов
линейно независимая.
Таким образом, векторы образуют базис подпространства
, а его размерность определяется количеством базисных векторов, т.е.
, что равносильно (9.3).
Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).
Действительно, для обратимости преобразования (см. свойство 6) его матрица
(размеров
) должна удовлетворять условиям (см. свойства 3,4,5):
Тогда по теореме 9.1 заключаем, что , т.е. матрица
— квадратная n-го порядка и невырожденная
, что и требовалось доказать.
Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
пространство – Линейное отображение
|
Пусть есть отображение $% phi: R^5 to R^3$% переводящие некоторые заданные векторы $%a_1, …, a_5$% в заданные векторы $%b_1, …, b_5$%. Векторы $%a_1, …, a_5$% линейно независимые. Как найти базис ядра и базис образа этого линейного отображения? |
Здравствуйте
Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
Ядро линейного отображения — это такое линейное подпространство области определения отображения, каждый элемент которого отображается в нулевой вектор [1][2]. А именно: если задано линейное отображение 



Свойства[править | править код]

Ядро и образ отображения
L.
Ядро отображения L — это линейное подпространство области определения V[4].
В линейном отображении 
Из этого следует, что образ L изоморфен факторпространству пространства V по ядру:
В случае, когда V конечномерно, из этого следует теорема о ранге и дефекте[en]:
где под рангом мы понимаем размерность образа отображения L, а под дефектом — размерность ядра отображения L[5].
Если V является предгильбертовым пространством, факторпространство 

Приложение к модулям[править | править код]
Понятие ядра также имеет смысл для гомоморфизмов модулей, которые являются обобщениями векторных пространств, где скаляры — элементы кольца, а не поля. Область определения отображения — это модуль с ядром, образующий подмодуль. Здесь концепции ранга и размерности ядра не обязательны.
В функциональном анализе[править | править код]
Если 





Представление в виде матричного умножения[править | править код]
Рассмотрим линейное отображение, представленное матрицей 







Ядро этого линейного отображения — это множество решений уравнения 



Матричное уравнение эквивалентно однородной системе линейных уравнений:
Тогда ядро матрицы 
Свойства подпространства[править | править код]
Ядро 





всегда содержит нулевой вектор, поскольку
.
- Если
и
, то
. Это следует из свойства дистрибутивности матричного умножения.
- Если
, а
является скаляром
, то
, поскольку
.
Пространство строк матрицы[править | править код]
Произведение 
Здесь 





Пространство строк, или кообраз матрицы 





Размерность пространства строк матрицы 



[5]
Левое нуль-пространство (коядро)[править | править код]
Левое нуль-пространство или коядро матрицы 







и левое нуль-пространство матрицы 

Неоднородные системы линейных уравнений[править | править код]
Ядро играет также большую роль при решении неоднородных систем линейных уравнений:
Пусть векторы 

Таким образом, разность любых двух решений системы 

Отсюда следует, что любое решение уравнения 


Геометрически это означает, что множество решений уравнения 


Иллюстрация[править | править код]
Ниже приведена простая иллюстрация вычисления ядра матрицы (см. Вычисление методом Гаусса ниже для метода, более подходящего для более сложных вычислений). Иллюстрация затрагивает также пространства строк и их связь с ядром.
Рассмотрим матрицу
Ядро этой матрицы состоит из всех векторов 
что можно выразить в виде однородной системы линейных уравнений относительно 


Те же самые равенства можно выписать в матричном виде:
С помощью метода Гаусса матрица может быть сведена к:
Преобразование матрицы в уравнения даёт:
Элементы ядра можно выразить в параметрическом виде следующим образом:
Поскольку 
Ядро матрицы 



Следующие скалярные произведения равны нулю:
что показывает, что вектора ядра матрицы 

Линейная оболочка этих двух (линейно независимых) вектор-строк — это плоскость, ортогональная вектору 
Поскольку ранг матрицы 


Примеры[править | править код]
-
,
- то ядром оператора L является множество решений системы
-
- Тогда ядро of L состоит из всех функций
, для которых
.
-
- Тогда ядро of D состоит из всех функций в
, производная которых равна нулю, то есть из всех постоянных функций.
-
- Тогда ядром оператора s будет одномерное подпространство, состоящее из всех векторов
.
Вычисления по методу Гаусса[править | править код]
Базис ядра матрицы можно вычислить с помощью метода Гаусса.
Для этой цели, если дана 

![{displaystyle left[{begin{array}{c}A\hline Eend{array}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f978cac52a35a542f8d6a1ed29debb8ff2e6d1c)


Если вычислим ступенчатый по столбцам вид матрицы методом Гаусса (или любым другим подходящим методом), мы получим матрицу ![{displaystyle left[{begin{array}{c}B\hline Cend{array}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23eb3e77c6f0f5d0f7b6beb321e501a19ba5190c)



Фактически вычисление может быть остановлено, как только матрица принимает ступенчатый по столбцам вид — остальное вычисление состоит из изменения базиса векторного пространства, образованного столбцами, верхняя часть которых равна нулю.
Например, представим, что
Тогда
Если привести верхнюю часть с помощью операций над столбцами к ступенчатому виду, получим
Последние три столбца матрицы 

являются базисом ядра матрицы 
Доказательство, что метод вычисляет ядро: поскольку операции над столбцами соответствуют умножению справа на обратимую матрицу, из факта, что ![{displaystyle left[{begin{array}{c}A\hline Eend{array}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16e875ad15a4391fb44e2e2e89a1e294502b27f2)
![{displaystyle left[{begin{array}{c}B\hline Cend{array}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a442c9b2ce18d358183bd22f68108996ffed4240)

![{displaystyle left[{begin{array}{c}A\hline Eend{array}}right]P=left[{begin{array}{c}B\hline Cend{array}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7281682377713bd63d90c3906686b919db93094c)
















Численные вычисления[править | править код]
Задача вычисления ядра на компьютере зависит от природы коэффициентов.
Точные коэффициенты[править | править код]
Если коэффициенты матрицы заданы как точные числа, ступенчатый вид матрицы может быть вычислен алгоритмом Барейса, который более эффективен, чем метод Гаусса. Ещё более эффективно использование сравнения по модулю и китайской теоремы об остатках, которые сводят задачу к нескольким аналогичным задачам над конечными полями (что сокращает издержки, порождённые нелинейной вычислительной сложностью целочисленного умножения).
Для коэффициентов из конечного поля метод Гаусса работает хорошо, но для больших матриц, которые случаются в криптографии и при вычислении базиса Грёбнера, известны более эффективные алгоритмы, которые имеют почти ту же вычислительную сложность, но работают быстрее и более подходят для современных компьютерных устройств.
Вычисления с плавающей точкой[править | править код]
Для матриц, элементами которых служат числа с плавающей запятой, задача вычисления ядра имеет смысл только для матриц, число строк которых равно её рангу — ввиду ошибок округления[en] матрицы с плавающими значениями почти всегда имеют полный ранг, даже когда они являются аппроксимацией матрицы много меньшего ранга. Даже для матрицы полного ранга можно вычислить её ядро только тогда, когда она хорошо обусловлена, то есть имеет низкое число обусловленности[6].
И для хорошо обусловленной матрицы полного ранга метод Гаусса не ведёт себя корректно: ошибки округления слишком велики для получения значимого результата. Так как вычисление ядра матрицы является специальным случаем решения однородной системы линейных уравнений, ядро может быть вычислено любым алгоритмом, предназначенным для решения однородных систем. Передовым программным обеспечением для этих целей является библиотека Lapack.
См. также[править | править код]
- Ядро (алгебра)
- Нуль функции
- Пространство столбцов
- Пространство функций[en]
- Альтернатива Фредгольма
Примечания[править | править код]
- ↑ The Definitive Glossary of Higher Mathematical Jargon — Null. Math Vault (1 августа 2019). Дата обращения: 9 декабря 2019.
- ↑ Weisstein, Eric W. Kernel. mathworld.wolfram.com. Дата обращения: 9 декабря 2019.
- ↑ Kernel (Nullspace) | Brilliant Math & Science Wiki. brilliant.org. Дата обращения: 9 декабря 2019.
- ↑ Линейная алгебра в том виде, как обсуждается в этой статье, является хорошо проработанной математической дисциплиной, для которой можно найти много книг. Почти весь материал статьи можно найти в лекциях Лея (Lay, 2005), Мейера (Meyer, 2001) и Стренга.
- ↑ 1 2 Weisstein, Eric W. Rank-Nullity Theorem. mathworld.wolfram.com. Дата обращения: 9 декабря 2019.
- ↑ Archived copy. Дата обращения: 14 апреля 2015. Архивировано 29 августа 2017 года.
Литература[править | править код]
- Sheldon Jay Axler. Linear Algebra Done Right. — 2nd. — Springer-Verlag, 1997. — ISBN 0-387-98259-0.
- Гилберт Стренг. Линейная алгебра и её применение. — Москва: «Мир», 1980.
- David C. Lay. Linear Algebra and Its Applications. — 3rd. — Addison Wesley, 2005. — ISBN 978-0-321-28713-7.
- Carl D. Meyer. Matrix Analysis and Applied Linear Algebra. — Society for Industrial and Applied Mathematics (SIAM), 2001. — ISBN 978-0-89871-454-8.
- David Poole. Linear Algebra: A Modern Introduction. — 2nd. — Brooks/Cole, 2006. — ISBN 0-534-99845-3.
- Howard Anton. Elementary Linear Algebra (Applications Version). — 9th. — Wiley International, 2005.
- Steven J. Leon. Linear Algebra With Applications. — 7th. — Pearson Prentice Hall, 2006.
- Serge Lang. Linear Algebra. — Springer, 1987. — ISBN 9780387964126.
- Lloyd N. Trefethen, David III Bau. Numerical Linear Algebra. — SIAM, 1997. — ISBN 978-0-89871-361-9.
Ссылки[править | править код]
- Hazewinkel, Michiel, ed. (2001), Kernel of a matrix, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Khan Academy, Introduction to the Null Space of a Matrix
Содержание
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом
ЛИНЕЙНОЕ ПРОСТРАНСТВО.
Линейное отображение
Линейным отображением линейного векторного пространства $ mathbb V_{} $ с операцией сложения векторов, обозначаемой $ +_{} $,
в линейное векторное пространство $ mathbb W_{} $ с операцией сложения векторов, обозначаемой $ boxplus_{} $,
называется функция (соответствие)
$$ mathcal A: mathbb V longmapsto mathbb W $$
(т.е. определенная на $ mathbb V_{} $, имеющая
значения в $ mathbb W_{} $), обладающая свойством линейности, которое описывается одним из двух эквивалентных представлений:
$$
mathcal A (X_1 +X_2)= mathcal A(X_1) boxplus mathcal A(X_2),quad mathcal A (alpha_1 X_1)=
alpha_1 mathcal A (X_1),
$$
или
$$
mathcal A(alpha_1 X_1 + alpha_2 X_2)= alpha_1 mathcal A(X_1) boxplus alpha_2 mathcal A(X_2)
$$
указанные свойства должны быть выполнены для любых векторов $ X_1,X_2 $ пространства $ mathbb V_{} $ и любых скаляров $ alpha_1,alpha_ 2 $ (вещественных если оба пространства
вещественны, и комплексных если хотя бы одно из пространств комплексное).
Если $ Y=mathcal A(X) $, то говорят, что $ Y_{} $ — образ вектора $ X_{} $, а $ X_{} $ —
прообраз вектора $ Y_{} $ при отображении $ mathcal A_{} $. Пространство $ mathbb V_{} $ называется областью определения отображения $ mathcal A_{} $.
Образно говоря, свойство линейности отображения заключается в том, что при этом отображении образ суммы любых двух векторов совпадает с суммой образов этих векторов, а произвольное растяжение прообраза влечет за собой сообразное же растяжение образа1).
Примеры линейных отображений
П
Пример 1. Рассмотрим линейное пространство
полиномов степени не выше $ n_{} $:
$$ mathbb P_n={p(x) in mathbb R[x] mid deg p(x) le n } , ; $$
в это же множество включаем и тождественно нулевой полином (для которого степень не определяется). Операция нахождения частного и операция нахождения остатка от деления полинома $ p(x)_{} $ на заданный фиксированный полином $ g(x) in mathbb R[x], g(x) notequiv 0 $ являются линейными отображениями пространства $ mathbb P_{n} $: если
$$ p_1(x)equiv q_1(x)g(x)+r_1(x), p_2(x)equiv q_2(x)g(x)+r_2(x) $$
при $ deg r_j(x)<deg g(x) $
то
$$
(alpha_1p_1(x)+alpha_2p_2(x)) equiv
$$
$$
equiv
(alpha_1q_1(x)+alpha_2q_2(x)) g(x) + (alpha_1r_1(x)+alpha_2r_2(x)) . $$
Фактически, операция деления на $ g_{}(x) $ (с остатком) порождает два разных линейных отображения. Если $ deg g(x) = m $ при $ 0<mle n $, то операция нахождения остатка — это отображение $ mathbb P_{n} mapsto mathbb P_{m-1} $, а операция нахождения частного — это отображение $ mathbb P_{n} mapsto mathbb P_{n-m} $.
П
Пример 2. В том же линейном пространстве $ mathbb P_{n}^{} $ операция дифференцирования
$$ frac{d }{d, x}: p(x) {color{Red}{ longmapsto} } p'(x) $$
является отображением $ mathbb P_{n}^{} $ в $ mathbb P_{n-1}^{} $ линейным
поскольку
$$frac{d }{d, x} (alpha_1 p_1(x) + alpha_2 p_2(x))=
alpha_1 frac{d }{d, x} p_1(x) + alpha_2 frac{d }{d, x} p_2(x)
.
$$
Прообраз любого элемента $ mathbb P_{n-1}^{} $ неединствен:
$ frac{d }{d, x}(frac{1}{2} x^2 + const)=x $.
П
Пример 3. Операцию нахождения первообразной:
$$
int_{0}^{x}:
begin{array}{ccc}
p(x) & {color{Red}{ longmapsto} } & int_{0}^{x} p(t) d, t \
a_0x^n+a_1x^{n-1}+cdots+a_n & {color{Red}{ longmapsto} } &
displaystyle frac{a_0}{n+1}x^{n+1}+frac{a_1}{n}x^{n}+cdots+a_nx
end{array}
$$
тоже можно рассматривать как линейное отображение
$ mathbb P_n {color{Red}{ longmapsto} } mathbb P_{n+1} $. При этом прообраз каждого полинома из
$ mathbb P_{n+1} $ (если существует) будет единствен.
П
Пример 4. Линейная форма от переменных $ x_{1},dots,x_n $:
$$mathcal A(x_1,dots,x_n)=a_1x_1+dots+a_nx_n,quad {a_j }_{j=1}^{n}
subset mathbb R $$
является примером линейного отображения $ mathbb R^{n}_{} $ в $ mathbb R_{} $. Здесь тоже
прообразов у одного и того же элемента из $ mathbb W_{} $ может быть несколько:
$$mathcal A(x_1,x_2)=2x_1-x_2 mbox{ отображает вектора } X_1=[0,0]
mbox{ и } X_2=[1,2] mbox{ в } 0 .$$
П
Пример 5. Обобщением предыдущего примера является
отображение $ mathcal A: mathbb R^n longmapsto mathbb R^m $, задаваемое
$$
mathcal A
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
= left(begin{array}{c}
a_{11}x_1+a_{12}x_2 + cdots + a_{1n}x_n \
dots \
a_{m1}x_1+a_{m2}x_2 + cdots + a_{mn}x_n
end{array}
right)=
$$
$$
=
left(begin{array}{cccc}
a_{11} & a_{12}& dots & a_{1n} \
dots & & & dots \
a_{m1} & a_{m2}& dots & a_{mn}
end{array}
right) cdot
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
$$
при произвольной вещественной матрице. Оно является линейным — в отличие от похожего на него отображения
$$
begin{array}{ll}
tilde{mathcal A}
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
&= left(begin{array}{c}
a_{11}x_1+a_{12}x_2 + cdots + a_{1n}x_n +b_1 \
dots \
a_{m1}x_1+a_{m2}x_2 + cdots + a_{mn}x_n + b_m
end{array}
right)= \
&=left(begin{array}{cccc}
a_{11} & a_{12}& dots & a_{1n} \
dots & & & dots \
a_{m1} & a_{m2}& dots & a_{mn}
end{array}
right) cdot
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)+
left(begin{array}{c}
b_1 \ vdots \ b_m
end{array}
right)
end{array}
$$
при хотя бы одном из чисел $ b_1,dots,b_{m} $ отличном от нуля. В самом деле, если записать последнее в матричном виде:
$$
tilde{mathcal A}(X)=Acdot X+ mathcal B,
$$
то
$$
tilde{mathcal A}(alpha X)=Acdot (alpha X)+ mathcal B ne alpha tilde{mathcal A}(X)=
alpha left(Acdot X+ mathcal B right).
$$
Для этого отображения свойство линейности не выполняется. Для отображений такого типа приходится расширять множество линейных отображений: см.
☟
AФФИННОЕ ОТОБРАЖЕНИЕ.
П
Пример 6. Предыдущим примерам
можно дать и геометрическую интерпретацию. Так, линейное отображение $ mathbb R^3 longmapsto mathbb R^3 $:
$$left(begin{array}{c}
x \ y \ z
end{array}
right) longmapsto
left(begin{array}{c}
x \ y \ 0
end{array}
right)
$$
задает ортогональную проекцию вектора $ X=(x,y,z) $ на плоcкость $ z=0 $.
Можно рассматривать его и как отображение $ mathbb R^{3} longmapsto mathbb R^2 $.
Проецирование же на произвольное подпространство может быть задано
с помощью матрицы. Так, например, отображение
$$left(begin{array}{c}
x \ y \ z
end{array}
right) longmapsto
frac{1}{3} left(begin{array}{rrr}
2 & -1 & -1 \
-1& 2 & -1 \
-1 & -1 & 2
end{array}
right)
left(begin{array}{c}
x \ y \ z
end{array}
right)
$$
задает ортогональную проекцию вектора $ X_{} $ на многообразие $ x+y+z=0 $.
Общее выражение для отображения ортогонального проецирования на линейное подпространство в $ mathbb R^{n}_{} $
☞
ЗДЕСЬ.
П
Пример 7. В линейном пространстве $ mathbb R^{mtimes n} $ матриц порядка $ mtimes n_{} $ с вещественными элементами определим два отображения:
$$ X mapsto Acdot X quad u quad X mapsto X cdot B $$
умножения слева на фиксированную матрицу $ A_{elltimes m} $ и умножения справа на также фиксированную матрицу $ B_{ntimes k} $.
Оба отображения являются линейными. Линейным также будет и отображение
$$ X mapsto Acdot X cdot B . $$
При дополнительных условиях $ m=n=ell=k $ линейным будет и отображение
$$ X mapsto Acdot X + X cdot B . $$
Оно отображает пространство $ mathbb R^{ntimes n} $ в себя.
П
Пример 8. В пространстве полиномов с вещественными коэффициентами от $ m_{} $ переменных $ x_1,x_2,dots,x_{m} $ степени не выше $ n_{} $ рассмотрим отображение
$$ f(x_1,x_2,dots,x_m) mapsto operatorname{grad} (f)= left(frac{partial f}{partial x_1}, frac{partial f}{partial x_2}, dots, frac{partial f}{partial x_m}
right) .
$$
Здесь вектор $ operatorname{grad} (f) $ называется градиентом функции $ f_{} $. Это отображение будет линейным. Для его записи используют следующий формализм. Вводят в рассмотрение специальный вектор, называемый набла2)
$$ nabla = left(frac{partial }{partial x_1}, frac{partial }{partial x_2}, dots, frac{partial }{partial x_m} right) . $$
Умножение этого вектора на функцию $ f_{} $ имеет результатом именно градиент:
$$ nabla cdot f = operatorname{grad} (f) . $$
Умножение же этого вектора по правилу скалярного произведения на вектор $ F= (f_1,f_2,dots,f_m) $,
состоящий из $ m_{} $ полиномов, порождает отображение этого вектора в полином:
$$ operatorname{div} (F) = langle nabla, F rangle =frac{partial f_1 }{partial x_1}+ frac{partial f_2 }{partial x_2}+ dots+ frac{partial f_m }{partial x_m} ; $$
он называется дивергенцией вектора $ F_{} $. Это отображение
$$ F mapsto operatorname{div} (F) $$
также будет линейным.
?
В частном случае линейных форм:
$$ f_j=a_{j1}x_1+dots+a_{jn}x_m quad npu quad jin{1,dots,m} $$
получим связь $ operatorname{div} (F) $ с одним объектом матричного анализа. Каким именно?
?
Является ли линейным отображение
$$ X longmapsto operatorname{Sp} (X) , $$
определенное в пространстве квадратных матриц порядка $ n_{} $? Здесь $ operatorname{Sp} (X) $ — след матрицы $ X_{} $.
?
Про линейное отображение $ mathcal A $ пространства $ mathbb R^{3}_{} $ в пространство $ mathbb P_3^{} $ известно, что
$$ mathcal A(1,0,1)=1+3,x+x^3, mathcal A(1,-1,0)=-1+x-x^2 . $$
Найти $ mathcal A(-1,2,1) $.
Свойства линейных отображений
§
В настоящем пункте $ mathbb O_{} $ означает нулевой вектор пространства $ mathbb V_{} $,
а $ mathbb O’ $ — нулевой вектор пространства $ mathbb W_{} $.
Два линейных отображения $ mathcal A $ и $ mathcal B $ из
$ mathbb V_{} $ в $ mathbb W_{} $ называются равными если $ mathcal A(X)=mathcal B(X) $ для любого
$ Xin mathbb V $. Нулевое отображение определяется условием
$${mathcal O}(X)=mathbb O’ quad npu quad forall Xin mathbb V .$$
Т
Теорема 1. Для любого линейного отображения $ mathcal A(X) $:
а) $ mathcal A(mathbb O)=mathbb O’ $;
б) если система $ {X_1,dots,X_k} $ линейно зависима, то и система $ { mathcal A(X_1),dots,mathcal A(X_k) } $ линейно зависима;
в) если система $ { mathcal A(X_1),dots,mathcal A(X_k) } $ линейно независима, то и система
$ {X_1,dots,X_k} $ линейно независима.
Т
Теорема 2. Линейное отображение отображает произвольное линейное многообразие пространства $ mathbb V_{} $ в линейное же многообразие пространства $ mathbb W_{} $.
Доказательство. Если
$$ mathbb M = X_0+mathcal L(X_1,dots,X_k)=
$$
$$
={X_0+alpha_1X_1+dots+ alpha_kX_k mid (alpha_1,dots,alpha_k)in mathbb R^k } ,
$$
то свойство линейности отображения $ mathcal A_{} $ дает:
$$
mathcal A( mathbb M) ={mathcal A(X_0)boxplus alpha_1mathcal A(X_1) boxplus dots boxplus alpha_kmathcal A(X_k) mid (alpha_1,dots,alpha_k)in mathbb R^k } =
$$
$$
=mathcal A(X_0) boxplus mathcal L(mathcal A(X_1),dots,mathcal A(X_k)) .
$$
Заметим, что в соответствии с теоремой 1, можно утверждать, что линейное отображение не увеличивает размерности отображаемого многообразия: $ dim mathcal A( mathbb M) le dim mathbb M $.
♦
=>
Линейное отображение отображает произвольную прямую пространства $ mathbb V_{} $ в прямую или точку пространства $ mathbb W $.
?
Доказать, что линейное отображение отображает параллельные многообразия пространства $ mathbb V_{} $ в параллельные же многообразия пространства $ mathbb W_{} $.
Т
Теорема 3. Пусть $ {X_1,dots,X_n} $ — произвольный базис $ mathbb V_{} $,
а $ Y_1,dots,Y_n $ — произвольные векторы из $ mathbb W_{} $. Существует единственное линейное отображение $ mathcal A: mathbb V longmapsto mathbb W $ такое, что$$ mathcal A(X_1)=Y_1,dots,mathcal A(X_n)=Y_n .$$
Иными словами: любое линейное отображение пространства $ mathbb V_{} $ в другое пространство однозначно определяется его заданием на базисных векторах пространства $ mathbb V_{} $.
Доказательство. Поскольку векторы $ X_1,dots,X_{n} $ — базисные, то существует
и единственно разложение любого $ Xin mathbb V_{} $: $ X=x_1X_1+cdots+x_nX_n $.
Зададим отображение $ mathcal A: mathbb V longmapsto mathbb W $ формулой
$$mathcal A(X) = x_1Y_1boxplus dots boxplus x_nY_n . $$
Легко проверить свойство его линейности. Кроме того:
$$mathcal A(X_j)=mathcal A(0cdot X_1+dots+1cdot X_j+dots+0cdot X_n)=
$$
$$
=0cdot Y_1 boxplus dots boxplus 1cdot Y_j boxplus dots boxplus 0cdot Y_n=Y_j,$$
т.е. оно удовлетворяет условиям теоремы.
Предположим теперь, что существует еще одно отображение $ mathcal B(X) $,
удовлетворяющее этим условиям: $ mathcal B(X_j)=Y_j $. Тогда
$$mathcal A(X)=x_1Y_1 boxplus cdots boxplus x_nY_n=
$$
$$
=x_1mathcal B(X_1) boxplus cdots boxplus x_nmathcal B(X_n)=mathcal B(X),$$
и, на основании определения, $ mathcal A(X)=mathcal B(X) $.
♦
Отображение $ {mathcal S}: mathbb V longmapsto mathbb W $ называется
суммой линейных отображений $ mathcal A $ и $ mathcal B $ если
$ mathcal S(X)=mathcal A(X) boxplus mathcal B(X) $ для $ forall Xin mathbb V_{} $. Отображение
$ mathcal F:mathbb V longmapsto mathbb W $ называется
произведением линейного отображения $ mathcal A_{} $ на число (скаляр)
$ lambda_{} in mathbb R $ если $ {mathcal F}(X)=lambda cdot mathcal A(X) $ для $ forall Xin mathbb V_{} $.
Т
Теорема 4. Отображения $ {mathcal S} $ и $ {mathcal F} $ — линейные.
П
Пример. В пространстве полиномов $ mathbb P_n $
операцию нахождения второй производной
$$ frac{d^2 }{d, x^2}:p(x) longmapsto p”(x)$$
тоже можно рассматривать как линейное отображение $ mathbb P_n longmapsto mathbb P_{n-1} $.
Линейным также будет и отображение
$$ frac{d^2 }{d, x^2}times Box + 2 frac{d}{d, x}times Box: p(x)
longmapsto p”(x)+2 p'(x) .$$
Т
Теорема 5. Множество $ {mathcal H}om(mathbb V,mathbb W) $ всех линейных
отображений из $ mathbb V_{} $ в $ mathbb W_{} $ образует линейное пространство и$$dim {mathcal H}om(mathbb V,mathbb W) = dim mathbb V cdot dim mathbb W .$$
Ядро и образ линейного отображения
Для линейного отображения $ mathcal A $ его ядром3) называется множество векторов из $ mathbb V_{} $, отображающихся в
$ mathbb O’ in mathbb W $:
$$mathcal{K}er (mathcal A)= left{Xin mathbb V big| mathcal A(X)=mathbb O’ right} ; $$
а его образом называется множество всех векторов из
$ mathbb W_{} $, для каждого из которых существует прообраз из $ mathbb V_{} $:
$$mathcal{I}m (mathcal A)= left{Yin mathbb W mid exists X in mathbb V, mathcal A(X)= Y
right} .$$
Фактически $ mathcal{I}m (mathcal A) $ можно назвать областью значений линейного отображения $ mathcal A_{} $.
Т
Теорема 1. $ mathcal{K}er (mathcal A) $ и $ mathcal{I}m(mathcal A) $ являются
линейными подпространствами соответствующих пространств.
Для линейного отображения $ mathcal A_{} $ его дефектом называется размерность ядра,
а его рангом — размерность образа:
$$ operatorname{dfc}(mathcal A )=dim (mathcal{K}er (mathcal A )) ,
operatorname{rank}(mathcal A )= dim (mathcal{I}m (mathcal A )) .
$$
Отображение называется невырожденным если $ operatorname{dfc}(mathcal A )=0 $.
Т
Теорема 2. Линейное отображение $ mathcal A $ невырождено тогда и только тогда, когда у каждого образа существует единственный прообраз.
Доказательство. Необходимость. Если $ mathcal A $ невырождено, то $ mathcal{K}er (mathcal A )={mathbb O} $, т.е. единственным вектором из $ mathbb V_{} $, отображающимся в $ mathbb O’ in mathbb W $ должен быть $ mathbb O_{} $. Если предположить неединственность прообраза для какого-то
$ Yin mathbb W $: $ Y=mathcal A (X_1)=mathcal A (X_2) $ при $ X_1ne X_2 $, то
$$mathbb O’=mathcal A (X_1)-mathcal A (X_2)=mathcal A (X_1-X_2)$$
и получаем противоречие с единственностью прообраза у $ mathbb O’ $.
Достаточность. Пусть $ mathcal A (X_1)ne mathcal A (X_2) $ для любых $ X_1ne X_2 $. Если бы $ mathcal{K}er (mathcal A ) $ имело ненулевую размерность, то существовал бы $ Xne mathbb O $ такой, что $ mathcal A (X)=mathbb O’ $, что противоречило бы предыдущей фразе: $ mathcal A (X)= mathcal A (mathbb O) $.
♦
Т
Теорема 3. Если $ {X_1,dots,X_{n}} $ — произвольный базис $ mathbb V_{} $,
то $ mathcal{I}m (mathcal A) $ совпадает с линейной оболочкой образов этих векторов$$ mathcal{I}m (mathcal A) ={mathcal L}left(mathcal A (X_1),dots, mathcal A (X_n) right) .$$
Доказательство. Действительно, любой вектор $ Y in mathcal{I}m (mathcal A) $ является
образом какого-то вектора $ X=x_1X_1+cdots+x_nX_n $, тогда на основании
линейности отображения:
$$ Y=mathcal A (X)=x_1mathcal A (X_1) boxplus cdots boxplus x_n mathcal A (X_n) in
{mathcal L}left(mathcal A (X_1),dots, mathcal A(X_n) right) .$$
Таким образом
$$mathcal{I}m (mathcal A) subset
{mathcal L}left(mathcal A (X_1),dots, mathcal A (X_n) right) .$$
Обратно, поскольку векторы $ mathcal A (X_1),dots, mathcal A (X_n) $ принадлежат
$ mathcal{I}m (mathcal A) $, то по теореме 1 и любая линейная комбинация
этих векторов должна принадлежать $ mathcal{I}m (mathcal A) $:
$${mathcal L}left(mathcal A (X_1),dots, mathcal A (X_n) right)
subset mathcal{I}m (mathcal A) .$$
Из двух взаимных включений множеств следует их равенство.
♦
П
Пример. Найти ядро и образ отображения $ mathbb R^3 longmapsto mathbb R^4 $
$$
mathcal A left(begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right)=
left(begin{array}{c}
x_3 \ 0 \x_1+x_2+x_3 \ x_1+x_2-x_3
end{array}
right) .
$$
Решение. Для определения $ mathcal{K}er (mathcal A) $ найдем фундаментальную
систему решений системы уравнений
$$left{ begin{array}{rrr}
x_3 &=&0 \
0 &=&0 \
x_1+x_2+x_3 &=&0 \
x_1+x_2-x_3 &=&0
end{array} right. quad Longrightarrow
X_1= left(begin{array}{r}
-1 \ 1 \0
end{array}
right)
$$
Имеем $ operatorname{dfc}(mathcal A )=1 $ и $ mathcal{K}er (mathcal A)= mathcal L (X_1) $.
Теперь для нахождения $ mathcal{I}m (mathcal A) $ воспользуемся теоремой 3:
базис следует искать среди векторов
$$Y_1=mathcal A left(begin{array}{c}
1 \ 0 \0
end{array}
right)= left(begin{array}{c}
0 \ 0 \ 1 \ 1
end{array}
right),
Y_2=mathcal A left(begin{array}{c}
0 \ 1 \0
end{array}
right)= left(begin{array}{c}
0 \ 0 \ 1 \ 1
end{array}
right),
$$
$$
Y_3=mathcal A left(begin{array}{c}
0 \ 0 \1
end{array}
right)= left(begin{array}{r}
1 \ 0 \ 1 \ -1
end{array}
right) .
$$
Имеем: $ operatorname{rank}(mathcal A )=2 $ и $ mathcal{I}m (mathcal A) = mathcal L (Y_1,Y_3) $.
♦
П
Пример. Найти ядро и образ отображения пространства полиномов $ mathbb P_3 $ в $ mathbb P_2 $, задаваемого формулой:
$$ mathcal A left(p(x)right) = x^2 p^{prime prime} (x) + p^{prime} (x) – 6, p(x) . $$
Решение. Для начала проверим, что это отображение именно $ mathbb P_3 mapsto mathbb P_2 $, т.е. при таком отображении происходит понижение степени полинома, по крайней мере на $ 1_{} $. И действительно, если $ p(x)=a_0x^3+a_1x^2+a_2x+a_3 $, то
$$ x^2 p^{prime prime} (x) + p^{prime} (x) – 6 p(x) equiv
$$
$$
equiv (-4,a_1+3,a_0)x^2+(2,a_1-6,a_2)x+(a_2-6,a_3) . $$
Теперь понятно, что $ mathcal{I}m (mathcal A) subset mathbb P_2 $, а, на самом деле, это включение может быть заменено на равенство. Действительно, в соответствии с теоремой 2, имеем:
$$ mathcal{I}m (mathcal A)= {mathcal L}left(mathcal A (1),mathcal A (x),mathcal A (x^2),mathcal A (x^3) right)=
$$
$$
= {mathcal L}left(-6,,-6,x+1 ,, -4,x^2+2,x ,, 3,x^2 right) = mathbb P_2 $$
поскольку три из четырех получившихся полиномов линейно независимы.
Теперь найдем $ mathcal{K}er (mathcal A) $, или, в альтернативной формулировке, подмножество решений дифференциального уравнения
$$ x^2 p^{prime prime} (x) + p^{prime} (x) – 6 p(x)=0 $$
во множестве $ mathbb P_3 $ (полиномов степени не выше третьей). Воспользуемся уже выведенной выше формулой для образа произвольного полинома $ p(x) in mathbb P_3 $.
Этот образ будет тождественно равным нулю полиномом при выполнении условий
$$ -4,a_1+3,a_0=0, 2,a_1-6,a_2=0, a_2-6,a_3=0 . $$
Решаем эту систему:
$$ a_0=frac{4}{3} a_1, a_2=frac{1}{3} a_1, a_3=frac{1}{18} a_1 . $$
Таким образом,
$$ mathcal{K}er (mathcal A) = left{ lambda (24,x^3+18,x^2+6,x+1) mid lambda in mathbb R right} . $$
♦
Т
Теорема 4. Пусть $ {X_1,dots,X_{{mathfrak{r}}}} $ — относительный базис $ mathbb V_{} $ над $ mathcal{K}er (mathcal{A}) $. Тогда система $ {mathcal{A}(X_1),dots,mathcal {A}(X_{{mathfrak{r}}}) } $ образует базис $ mathcal{I}m (mathcal{A}) $.
Доказательство. Любой вектор $ Xin mathbb V $ представи́м в виде $ X=X_{ast}+alpha_1X_1+dots+ alpha_{{mathfrak{ r}}}X_{{mathfrak{r}}} $, где $ X_{ast} in mathcal{K}er (mathcal{A}) $. Тогда $ mathcal{A}(X) in mathcal{L} ( mathcal{A}(X_1),dots, mathcal{A}(X_{{mathfrak {r}}})) $ и, следовательно,
$$ mathcal{I}m (mathcal{A}) = mathcal L ( mathcal{A}(X_1),dots, mathcal{A}(X_{{mathfrak{r}}})) . $$
Если векторы $ mathcal{A}(X_1),dots,mathcal{A}(X_{{mathfrak{r}}}) $ удовлетворяют равенству:
$$ beta_1 mathcal{A}(X_1) boxplus dots boxplus beta_{{mathfrak{r}}} mathcal{A}(X_{{mathfrak{r}}})= mathbb O’ , $$
то $ beta_1 X_1 + dots + beta_{{mathfrak{r}}} X_{{mathfrak{r}}} in mathcal{K}er (mathcal{A}) $. На основании определения относительного базиса из такого равенства необходимо следует $ beta_1 = dots = beta_{{mathfrak{r}}}=0 $. Таким образом,
система $ {mathcal A(X_1),dots,mathcal A(X_{{mathfrak{r}}}) } $ л.н.з.
♦
Т
Теорема 5. Имеет место равенство:
$$ dim mathbb V=dim left( mathcal{K}er (mathcal A) right) + dim left( mathcal{I}m (mathcal A) right) = operatorname{dfc}(mathcal A )+ operatorname{rank}(mathcal A ) .$$
Доказательство
☞
ЗДЕСЬ.
Утверждение $ mathbb V= mathcal{K}er (mathcal A) oplus mathcal{I}m (mathcal A) $ (здесь $ oplus $ означает прямую сумму подпространств ),
вообще говоря, неверно!
Т
Теорема 6. Пусть $ mathbb V_1 $ — линейное подпространство $ mathbb V_{} $, а $ mathbb W_1 $ — линейное подпространство $ mathbb W $, причем
$$
dim mathbb V_1 + dim mathbb W_1 =dim mathbb V .
$$
Тогда существует линейное отображение
$ mathcal A : mathbb V longmapsto mathbb W $ такое, что
$$
mathcal{K}er (mathcal A ) =mathbb V_1 , quad mathcal{I}m (mathcal A )=mathbb W_1 .
$$
Определенные в настоящем пункте множества $ mathcal{K}er (mathcal A) $ и $ mathcal{I}m(mathcal A) $ позволяют полностью решить и следующую задачу:
Задача. Установить множество всех прообразов вектора $ Y ne mathbb O^{prime} $ при линейном отображении $ mathcal A_{} $ .
Т
Теорема 7. Если $ Y notin mathcal{I}m(mathcal A) $, то у вектора $ Y in mathbb W $ не существует прообраза в $ mathbb V_{} $. Если $ X_{0} in mathbb V $ — какой-то из прообразов вектора $ Y_{} $, то все множество прообразов этого вектора является линейным многообразием в $ mathbb V_{} $, а именно:
$$ X_0 + mathcal{K}er (mathcal A) . $$
Матрица линейного отображения
Рассмотрим линейное отображение $ mathcal A: mathbb V longmapsto mathbb W $,
и пусть $ {X_1,dots,X_n} $ — базис $ mathbb V_{} $, а
$ {Y_1,dots,Y_m} $ — базис $ mathbb W_{} $. Найдем координаты векторов
$ mathcal A(X_1),dots,mathcal A(X_n) $ в базисе $ {Y_1,dots,Y_m} $:
$$
left{ begin{array}{ccr}
mathcal A(X_1)&=&{color{RubineRed} alpha }_{11}Y_1 boxplus {color{RubineRed} alpha }_{21}Y_2 boxplus dots boxplus {color{RubineRed} alpha }_{m1}Y_m, \
mathcal A(X_2)&=&{color{Green} alpha }_{12}Y_1 boxplus {color{Green} alpha }_{22}Y_2 boxplus dots boxplus {color{Green} alpha }_{m2}Y_m, \
dots & & dots, \
mathcal A(X_n)&=&alpha_{1n}Y_1 boxplus alpha_{2n}Y_2 boxplus dots boxplus alpha_{mn}Y_m.
end{array} right.
$$
Матрица
$$
{mathbf A}= left(begin{array}{cccc}
{color{RubineRed} alpha } _{11} & {color{Green} alpha }_{12}& dots & alpha_{1n} \
{color{RubineRed} alpha } _{21} & {color{Green} alpha }_{22}& dots & alpha_{2n} \
vdots & & & vdots \
{color{RubineRed} alpha } _{m1} & {color{Green} alpha }_{m2}& dots & alpha_{mn}
end{array}
right)_{mtimes n},
$$
по столбцам которой стоят координаты образов базисных векторов, называется матрицей линейного отображения $ mathcal A_{} $ в выбранных базисах.
Почему запись координат в матрицу производится по столбцам? Казалось бы, естественней ставить их по строкам ![]() Объяснение этому решению будет дано ниже.
Объяснение этому решению будет дано ниже.
Т
Теорема 1. Координаты произвольного вектора
$ X=x_1X_1+dots+x_nX_n $ и его образа $ mathcal A (X)=y_1Y_1 boxplus dots boxplus y_mY_m $
связаны формулой:
$$
left(begin{array}{l}
y_1 \ vdots \ y_m
end{array}
right) =
{mathbf A}left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) .
$$
Вот именно для этой последней формулы необходимо было «транспонировать» запись матрицы линейного отображения в начале настоящего пункта.
Доказательство. С помощью приведенных выше формул для $ mathcal A (X_1), dots, mathcal A (X_n) $ получаем:
$$
begin{array}{rcl}
mathcal A (X)&=&mathcal A (x_1X_1+dots+x_nX_n)=x_1mathcal A (X_1) boxplus dots boxplus
x_nmathcal A (X_n)= \
&=&x_1 (alpha_{11}Y_1 boxplus dots boxplus alpha_{m1}Y_m) boxplus dots boxplus
x_n(alpha_{1n}Y_1 boxplus dots boxplus alpha_{mn}Y_m)= \
&=&underbrace{(x_1alpha_{11} +dots+x_nalpha_{1n})}_{y_1}Y_1 boxplus dots boxplus
underbrace{(x_1alpha_{m1}+dots+x_nalpha_{mn})}_{y_m}Y_m,
end{array}
$$
откуда и следует утверждение теоремы.
♦
П
Пример. Найти матрицу линейного отображения
$$
mathcal A left(begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right)=
left(begin{array}{c}
x_3 \ 0 \x_1+x_2+x_3 \ x_1+x_2-x_3
end{array}
right)
$$
в стандартных базисах пространств
$$
overbrace{left{underbrace{left[ begin{array}{c} 1 \ 0 \ 0 end{array} right]}_{=mathfrak e_{_1}} ,
underbrace{left[ begin{array}{c} 0 \ 1 \ 0 end{array} right]}_{=mathfrak e_{_2}},
underbrace{left[ begin{array}{c} 0 \ 0 \ 1 end{array} right]}_{=mathfrak e_{_3}}
right}}^{mathbb R^3} quad u quad
overbrace{left{
underbrace{left[ begin{array}{c} 1 \ 0 \ 0 \ 0 end{array} right]}_{={mathfrak E_{_1}}} ,
underbrace{left[ begin{array}{c} 0 \ 1 \ 0 \0 end{array} right]}_{=mathfrak E_{_2}},
underbrace{left[ begin{array}{c} 0 \ 0 \ 1 \0 end{array} right]}_{=mathfrak E_{_3}} ,
underbrace{left[ begin{array}{c} 0 \ 0 \ 0 \1 end{array} right]}_{=mathfrak E_{_4}}
right}
}^{mathbb R^4}
$$
Решение.
$$ mathcal A(mathfrak e_1)=
left[ begin{array}{c} 0 \ 0 \ 1 \ 1 end{array} right]=0cdot mathfrak E_{_1}+0cdot mathfrak E_{_2}+1cdot mathfrak E_{_3}+1cdot mathfrak E_{_4} ;quad mathcal A(mathfrak e_2)=
left[ begin{array}{c} 0 \ 0 \ 1 \ 1 end{array} right]=0cdot mathfrak E_{_1}+0cdot mathfrak E_{_2}+1cdot mathfrak E_{_3}+1cdot mathfrak E_{_4} ;
$$
$$
mathcal A(mathfrak e_3)=
left[ begin{array}{r} 1 \ 0 \ 1 \ -1 end{array} right]=1cdot mathfrak E_{_1}+0cdot mathfrak E_{_2}+1cdot mathfrak E_{_3}-1cdot mathfrak E_{_4} .
$$
Матрица отображения $ mathcal A_{} $ в выбранных базисах:
$$ mathbf A=
left(begin{array}{ccr}
0 & 0 & 1 \
0 & 0 & 0 \
1& 1 & 1 \
1 & 1 & -1
end{array}
right)
$$
совпадает с матрицей коэффициентов при переменных $ x_1,x_2,x_3 $ в выражениях координат вектора $ mathcal A(X) $.
♦
П
Пример. Найти матрицу линейного отображения пространства полиномов $ mathbb P_3 $ в $ mathbb P_2 $, задаваемого формулой:
$$ mathcal A left(p(x)right) = x^2 p^{prime prime} (x) + p^{prime} (x) – 6 p(x) . $$
Базисом пространства $ mathbb P_3 $ выбран $ {1,x,x^2,x^3} $, а базис пространства
$ mathbb P_2 $ состоит из полиномов Лежандра
$$ {P_0(x)=1, P_1(x)= x, P_2(x)=frac{1}{2}(3,x^2-1) } .$$
Решение. В предыдущем ПУНКТЕ уже были получены выражения:
$$ mathcal A(1)=-6, mathcal A(x)=-6,x+1, mathcal A(x^2)=-4,x^2+2,x
, mathcal A(x^3)=3,x^2 .$$
Если бы базис пространства $ mathbb P_2 $ составляли полиномы, входящие в базис исходного пространства,
т.е. $ {1,x,x^2} $, то матрица линейного отображения построилась бы достаточно просто:
$$
mathbf B=
left(
begin{array}{rrrr}
-6 & 1 & 0 & 0 \
0 &-6 & 2 & 0 \
0 & 0 & -4 & 3 \
end{array}
right) .
$$
Однако базис пространства $ mathbb P_2 $ отличается от $ {1,x,x^2} $ в последнем полиноме: $ P_2(x) notequiv x^2 $. Координаты $ mathcal A(1) $ и $ mathcal A(x) $ остаются прежними, а вот $ mathcal A(x^2) $ и $ mathcal A(x^3) $ приходится переписывать под базис из полиномов Лежандра:
$$ -4,x^2+2,x equiv a_{13}cdot 1 + a_{23}cdot x + a_{33} cdot left( frac{1}{2}(3,x^2-1)
right) . $$
Откуда получаем: $ a_{13}=-4/3, a_{23}=2, a_{33}=-8/3 $. Аналогично
$$ 3,x^2equiv P_0(x)+2,P_2(x) $$
и, следовательно, матрица линейного отображения:
$$
mathbf A=
left(
begin{array}{rrrr}
-6 & 1 & -4/3 & 1 \
0 &-6 & 2 & 0 \
0 & 0 & -8/3 & 2 \
end{array}
right) .
$$
♦
Т
Теорема 2. Существует изоморфизм между линейным пространством $ {mathcal H}om(mathbb V,mathbb W) $ (линейных отображений из $ mathbb V_{} $ в $ mathbb W_{} $)
и линейным пространством матриц $ mathbb R^{mtimes n } $.
Фактически теоремы $ 1_{} $ и $ 2_{} $ сводят рассмотрение произвольного линейного отображения $ mathcal A_{} $ пространства $ mathbb V_{} $ в пространство $ mathbb W_{} $ к рассмотрению отображения арифметического пространства $ n_{} $-компонентных столбцов в арифметическое пространство $ m_{} $-компонентных столбцов
$$ Y=mathbf AX quad mbox{ при } quad Xin mathbb R^n, Yin mathbb R^m ; $$
это отображение задается $ mtimes n_{} $-матрицей $ mathbf A_{} $. Получается, что для полного задания исходного линейного отображения достаточно знать только результат его действия на базисные векторы пространства $ mathbb V_{} $. После фиксирования базисов обоих пространств и установления матрицы линейного отображения, можно «забыть» о природе этих пространств и исследовать свойства отображения в «переводе на язык» умножения матрицы на столбец. В частности, «почти даром» получаем следующий результат:
Т
Теорема 3. Если $ A_{} $ — матрица линейного отображения $ mathcal A_{} $ в каких-то выбранных базисах пространств $ mathbb V_{} $ и $ mathbb W_{} $, то
$$operatorname{rank} (mathcal A)=operatorname{rank}( A ), operatorname{dfc} (mathcal A)=n-operatorname{rank}( A ) .$$
Ядро линейного отображения
$$ Y=AX quad mbox{ при } quad Xin mathbb R^n, Yin mathbb R^m, quad A in mathbb R^{mtimes n } $$
часто называется ядром матрицы $ A_{} $ или нуль-пространством матрицы $ A_{} $ и также обозначается $ {mathcal K}er (A) $. Наряду с определением ядра матрицы через свойства отображения
$ AX $, можно дать ему и другую интерпретацию:
Т
Теорема 4. Если в пространстве $ mathbb R_{}^{n} $, рассматриваемом как пространство $ n_{} $-строк, ввести скалярное произведение формулой
$$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n quad npu quad X=[x_1,x_2,dots,x_n], Y=[y_1,y_2,dots,y_n] , $$
то $ {mathcal K}er (A) $ образует ортогональное дополнение линейной оболочки строк этой матрицы в пространстве $ mathbb R_{}^{n} $:
$$ {mathcal K}er (A) bot mathcal L ( A^{[1]}, A^{[2]},dots, A^{[m]} ),
{mathcal K}er (A) oplus mathcal L ( A^{[1]}, A^{[2]},dots, A^{[m]} ) = mathbb R_{}^{n} .
$$
Дефектом матрицы4) $ A_{} $ будем называть размерность ядра этой матрицы, или, что то же, число элементов фундаментальной системы решений системы линейных однородных уравнений $ AX=mathbb O $. В соответствии с результатами, приведенными
☞
ЗДЕСЬ:
$$ operatorname{dfc}(A) = n – mathfrak r npu mathfrak r = operatorname{rank}(A) . $$
Вернемся теперь к общему случаю линейного пространства.
Задача. Как изменяется матрица линейного отображения $ mathcal A_{} $ при изменении
базисов?
Т
Теорема 5. Пусть $ {{mathfrak X}_1,dots,{mathfrak X}_n } $ — новый базис пространства $ mathbb V_{} $, $ { {mathfrak Y}_1,dots,{mathfrak Y}_m } $— новый базис $ mathbb W_{} $, и в этих
базисах линейное отображение $ mathcal A $ имеет матрицу $ {mathbf B} $. Если $ C_{} $ — матрица перехода от старого базиса к новому в пространстве $ mathbb V_{} $, а $ D_{} $ — матрица перехода от старого базиса к новому в пространстве $ mathbb W_{} $, то
$$ {mathbf B}=D^{-1}cdot {mathbf A} cdot C . $$

Доказательство. Действительно, координаты произвольного вектора
$$ X=x_1X_1+dots+x_nX_n = {mathfrak x}_1 {mathfrak X}_1+dots+ {mathfrak x}_n {mathfrak X}_n ,$$
и его образа
$$ Y =mathcal A(X)=y_1Y_1 boxplus dots boxplus y_mY_m= {mathfrak y}_1{mathfrak Y}_1 boxplus dots boxplus {mathfrak y}_m{mathfrak Y}_m $$
связаны следующими соотношениями: с одной стороны, на основании теоремы 1,
$$
left(begin{array}{c}
y_1 \ vdots \ y_m
end{array}
right) = {mathbf A}left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right), qquad
left(begin{array}{c}
{mathfrak y}_1 \ vdots \ {mathfrak y}_m
end{array}
right) = {mathbf B}left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right) .
$$
с другой стороны, на основании результатов пункта
☞
ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ЗАМЕНЕ БАЗИСА,
$$
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)=C left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right),
qquad
left(begin{array}{c}
y_1 \ vdots \ y_m
end{array}
right)=D left(begin{array}{c}
{mathfrak y}_1 \ vdots \ {mathfrak y}_m
end{array}
right).
$$
Получаем цепочку равенств:
$$
{mathbf B}left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right)=
left(begin{array}{c}
{mathfrak y}_1 \ vdots \ {mathfrak y}_m
end{array}
right) =D^{-1}left(begin{array}{c}
y_1 \ vdots \ y_m
end{array}
right)=D^{-1} {mathbf A}left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)=D^{-1} {mathbf A} C left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right).
$$
Поскольку равенство справедливо для любого столбца координат, то оно справедливо и для столбцов
$$
left(begin{array}{c}
1 \ 0 \ vdots \ 0
end{array}
right) ,
left(begin{array}{c}
0 \ 1 \ vdots \ 0
end{array}
right)
,dots,
left(begin{array}{c}
0 \ 0 \ vdots \ 1
end{array}
right) .
$$
Объединяя полученные $ n_{} $ равенств в одно матричное, получаем $ {mathbf B}E = D^{-1} {mathbf A} C E $, где $ E_{} $ — единичная матрица порядка $ n_{} $. Отсюда и следует утверждение теоремы.
♦
Канонический вид матрицы линейного отображения
Задача. Подобрать базисы пространств $ mathbb V_{} $ и $ mathbb W_{} $ так, чтобы матрица заданного линейного отображения $ mathcal A $ имела наиболее простой вид.
Найдем относительный базис $ mathbb V_{} $ над $ mathcal{K}er (mathcal A) $, т.е. базис $ mathcal{K}er (mathcal A) $ дополним до базиса $ mathbb V_{} $:
$$
{X_1,dots,X_{{mathfrak r}}} gets mbox{ относительный базис }
mathbb V mbox{ над } mathcal{K}er (mathcal A)
$$
$$
{X_{{mathfrak r}+1},dots,X_{n} } gets mbox{ базис } mathcal{K}er (mathcal A)
$$
Было доказано (см.
☞
теорему 4 ), что $ {mathcal A(X_1),dots,mathcal A(X_{{mathfrak r}}) } subset mathbb W $ является базисом $ mathcal{I}m (mathcal A) $. Составим базис $ mathbb W_{} $ ее дополнением:
$$
{mathcal A(X_1),dots,mathcal A(X_{{mathfrak r}})} gets
mbox{ базис } mathcal{I}m (mathcal A)
$$
$$
{ Y_{{mathfrak r}+1},dots,Y_{m}} gets mbox{ относительный базис }
mathbb W mbox{ над } mathcal{I}m (mathcal A)
$$
Т
Теорема. В выбранных базисах матрица линейного отображения $ mathcal A $ имеет следующий канонический вид:
$$
{mathbf B}=left( begin{array}{cccccc}
1 & & & & \
&1 & & &mathbb O\
& &ddots& & \
& & & 1 & \
& & & & \
&mathbb O & & & mathbb O
end{array}
right)
begin{array}{r}
left. begin{array}{r}
\ \ \ \ end{array} right} \
\ \
end{array}
begin{array}{r}
\ \ {mathfrak r} \ \ \
\ \
end{array}
= left( begin{array}{ll}
E_{{mathfrak r}times {mathfrak r}} & mathbb O_{{mathfrak r}times (n-{mathfrak r})} \
mathbb O_{(m-{mathfrak r})times {mathfrak r}} & mathbb O_{(m-{mathfrak r})times (n-{mathfrak r})}
end{array}
right) .
$$
Здесь $ {mathfrak r}= operatorname{rank} (mathcal A) $.
Доказательство. Разложим образы базисных векторов $ {X_1,dots,X_n} $ по базису пространства $ mathbb W $:
$$
begin{array}{llllllll}
mathcal A(X_1) & = 1cdot mathcal A(X_1) & boxplus 0 cdot mathcal A(X_2) & boxplus dots & boxplus 0cdot mathcal A(X_{mathfrak r})&
boxplus 0cdot Y_{{mathfrak r}+1}&boxplusdots &boxplus 0cdot Y_m, \
mathcal A(X_2) & = 0cdot mathcal A(X_1) & boxplus 1 cdot mathcal A(X_2) & boxplus dots & boxplus 0cdot mathcal A(X_{mathfrak r})&
boxplus 0cdot Y_{{mathfrak r}+1}&boxplus dots & boxplus 0cdot Y_m, \
dots & & & dots \
mathcal A(X_{mathfrak r}) & = 0cdot mathcal A(X_1) & boxplus 0 cdot mathcal A(X_2) & boxplus dots & boxplus 1cdot mathcal A(X_{mathfrak r})&
boxplus 0cdot Y_{{mathfrak r}+1}&boxplus dots & boxplus 0cdot Y_m,
end{array}
$$
а $ mathcal A(X_{{mathfrak r}+1})=mathbb O^{prime},dots, mathcal A(X_{m})=mathbb O^{prime} $ по определению
$ mathcal{K}er (mathcal A) $.
♦
Матричный формализм
§
Настоящий пункт может быть пропущен при первоначальном чтении.
В частном случае отображения $ mathbb R^{n} $ в $ mathbb R^{m} $, задаваемого матрицей в стандартных базисах пространств, результат последнего пункта можно переформулировать в следующем виде.
Т
Теорема. Любую матрицу $ A_{mtimes n} $ ранга $ mathfrak r > 0 $ можно представить в виде произведения
$$ A=Dcdot A_d cdot tilde C $$
при
$$
A_d =left( begin{array}{cccccc}
1 & & & & \
&1 & & &mathbb O\
& &ddots& & \
& & & 1 & \
& & & & \
&mathbb O & & & mathbb O
end{array}
right)
begin{array}{r}
left. begin{array}{r}
\ \ \ \ end{array} right} \
\ \
end{array}
begin{array}{r}
\ \ {mathfrak r} \ \ \
\ \
end{array}
= left( begin{array}{ll}
E_{{mathfrak r}times {mathfrak r}} & mathbb O_{{mathfrak r}times (n-{mathfrak r})} \
mathbb O_{(m-{mathfrak r})times {mathfrak r}} & mathbb O_{(m-{mathfrak r})times (n-{mathfrak r})}
end{array}
right) $$
и при невырожденных матрицах $ D_{mtimes m} $ и $ tilde C_{ntimes n} $.
Здесь матрица $ tilde C $ соответствует матрице $ C^{-1} $ из теоремы предыдущего пункта.
П
Пример. Представить матрицу
$$ A =
left(
begin{array}{rrr}
2 & – 1 & 0 \
-2/3 & 5/3 & 4/3 \
2 & – 1 & 0 \
-2/3 & 5/3 & 4/3
end{array}
right)
$$
в виде произведения из теоремы.
Решение. Здесь $ operatorname{rank} (A) =2 $, так что
$$
A_d=
left(begin{array}{ccc}
1 & 0 & 0 \
0 & 1 & 0 \
0 & 0 & 0 \
0 & 0 & 0
end{array}
right) , .
$$
Для нахождения матрицы $ C $ из теоремы предыдущего пункта ищем базис ядра отображения $ AX $, т.е. попросту говоря, фундаментальную систему решений системы уравнений $ AX=mathbb O $. Можно взять $ X=[1,2,-2]^{top} $. Этот столбец будет третьим столбцом матрицы $ C $. Первые два — любые линейно независимые с этим столбцом. Например
$$
C=
left(begin{array}{ccr}
1 & 0 & 1 \
0 & 1 & 2 \
0 & 0 & -2
end{array}
right) , .
$$
Теперь умножаем столбцы $ C_{[1]} $ и $ C_{[2]} $ на матрицу $ A $ (слева). Полученные столбцы
$$
D_{[1]}=left[2,-2/3,2,-2/3right]^{top}, D_{[2]}=left[-1,5/3,-1,5/3right]^{top}
$$
будут первыми столбцами искомой матрицы $ D $. Оставшиеся два выбираем произвольными линейно независимыми с уже найденными.
$$
D=
left(
begin{array}{rrrr}
2 & – 1 & 1 & 0 \
-2/3 & 5/3 & 0 & 1 \
2 & -1 & 0 & 0 \
-2/3 & 5/3 & 0 & 0
end{array}
right), quad tilde C= C^{-1} =
left(
begin{array}{rrr}
– 1 & 0 & 1/2 \
0 & 1 & 1 \
0 & 0 & -1/2
end{array}
right) , .
$$
♦
Разложение матрицы в произведение из теоремы не единственно. Так, например, матрицу $ tilde C $ можно выбрать в классе ортогональных матриц. Из этого замечания можно «перебросить мостик» к похожему разложению матрицы в произведение, известному как сингулярное разложение. Очень полезно в задачах обработки данных.
Линейный оператор
Линейное отображение векторного пространства $ mathbb V_{} $
в себя
$$ mathcal A : mathbb V longmapsto mathbb V $$
называется линейным преобразованием $ mathbb V_{} $ или линейным оператором на $ mathbb V_{} $. Подробнее
☞
ЗДЕСЬ.
Аффинное отображение
Линейные отображения пространства $ mathbb V_{} $ в пространство $ mathbb W_{} $ составляют подмножество более широкого класса отображений.
Рассмотрим пример $ 5_{} $
☞
ЗДЕСЬ. Отображение пространства $ mathbb R^{n}_{} $ в пространство $ mathbb R^{m} $, задаваемое соотношением
$$
begin{array}{ll}
tilde{mathcal A}
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
&= left(begin{array}{c}
a_{11}x_1+a_{12}x_2 + cdots + a_{1n}x_n +b_1 \
dots \
a_{m1}x_1+a_{m2}x_2 + cdots + a_{mn}x_n + b_m
end{array}
right)= \
&=left(begin{array}{cccc}
a_{11} & a_{12}& dots & a_{1n} \
dots & & & dots \
a_{m1} & a_{m2}& dots & a_{mn}
end{array}
right) cdot
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)+
left(begin{array}{c}
b_1 \ vdots \ b_m
end{array}
right)
end{array}
$$
будет линейным отображением при условии, что $ b_1=0,dots, b_m=0 $ и не будет линейным отображением при хотя бы одном из чисел $ b_1,dots,b_{m} $ отличном от нуля.
Тем не менее, по своему внешнему виду отображение из $ mathbb R^{n}_{} $ в $ mathbb R^{m} $, задаваемое в матричном виде как $ A, X + mathcal B $ напоминает линейную функцию $ a, x+b $, действующую в $ mathbb R $. Кажется очень несправедливым лишать подобные отображения эпитета линейный, однако же именно это и произошло в линейной алгебре и геометрии.
Аффинным5) отображением линейного векторного пространства $ mathbb V_{} $ с операцией сложения векторов, обозначаемой $ +_{} $,
в линейное векторное пространство $ mathbb W_{} $ с операцией сложения векторов, обозначаемой $ boxplus_{} $,
называется функция вида
$$ mathcal A(X) boxplus_{} mathcal B npu X in mathbb V . $$
Здесь $ mathcal A $ — линейное отображение $ mathbb V_{} $ в $ mathbb W_{} $, а $ mathcal B $ — некоторый вектор пространства $ mathbb W_{} $.
Образно говоря, аффинное отображение может быть получено сдвигом некоторого линейного отображения. Фактически же определение содержит в себе объяснение той причины, по которой аффинные отображения изучаются менее подробно, чем линейные: первые сводятся ко вторым.
Основное геометрическое свойство аффинного отображения проявилось в
☞
ПУНКТЕ для отображения линейного.
Т
Теорема. Аффинное отображение отображает произвольное линейное многообразие пространства $ mathbb V_{} $ в линейное же многообразие пространства $ mathbb W_{} $. Аффинное отображение отображает параллельные многообразия пространства $ mathbb V_{} $ в параллельные же многообразия пространства $ mathbb W_{} $.
=>
Аффинное отображение отображает произвольную прямую пространства $ mathbb V_{} $ в прямую или точку пространства $ mathbb W $.
Почему рассматриваются только линейные отображения?
Почему во всех вузовских курсах алгебры не рассматриваются более сложные отображения, задаваемые, например, нелинейными полиномами:
$$
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) mapsto
left(
begin{array}{c}
x_1^4-sqrt{2} x_1^2x_3 + 17, x_2^5+2, x_1 – 3,x_3-14 \
x_2^{18}- x_2^7+x_1x_2^4x_3^6-x_1-5,x_2+2 \
x_2x_3^3+x_3-6 \
x_1-2,x_2+6,x_3-33
end{array}
right) ?
$$
— Да потому что про них мало что понятно. Попытки обобщения на нелинейный случай практически любого понятия, введенного для линейного отображения, приводят к нерешенной задаче. Так, для обобщения понятия ядра придется решить не решенную на настоящий момент 16-ю проблему Гильберта;
еще одна нерешенная проблема — проблема якобиана — связана с существованием обратного к полиномиальному отображению.
В одном частном случае нелинейные отображения сравнительно хорошо изучены — это отображения $ mathbb R^2 mapsto mathbb R^2 $, заданные условиями:
$$
left(
begin{array}{l}
x \
y
end{array}
right) mapsto
left(
begin{array}{l}
u(x,y) \
v(x,y)
end{array}
right) quad npu quad frac{partial u}{partial x}=frac{partial v}{partial y}, frac{partial u}{partial y}=-frac{partial v}{partial x} ;
$$
(функции $ u_{} $ и $ v_{} $ — не обязательно полиномы).
Последние два условия называются условиями Коши-Римана (Даламбера-Эйлера); из них следует, что каждая из функций $ u_{} $ и $ v_{} $ является гармонической функцией, т.е. удовлетворяет тождествам:
$$
frac{partial^2 u}{partial x^2}+frac{partial^2 u}{partial y^2}equiv 0,quad frac{partial^2 v}{partial x^2}+frac{partial^2 v}{partial y^2} equiv 0 .
$$
Подобные отображения рассматриваются в разделе математики, известном как КОМПЛЕКСНЫЙ АНАЛИЗ или теория функций комплексной переменной (ТФКП).
Как же исследовать нелинейные отображения в общем случае? — Ну, по крайней мере, можно попытаться свести их исследование к линейному случаю. Рассмотрим пример отображения из начала
пункта
$$
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) mapsto
left(
begin{array}{c}
x_1^4-sqrt{2} x_1^2x_3 + 17, x_2^5+2, x_1 – 3,x_3-14 \
x_2^{18}- x_2^7+x_1x_2^4x_3^6-x_1-5,x_2+2 \
x_2x_3^3+x_3-6 \
x_1-2,x_2+6,x_3-33
end{array}
right) =
$$
$$
=left(
begin{array}{r}
-14 \
2 \
-6 \
-33
end{array}
right)
+
left(
begin{array}{c}
2, x_1 – 3,x_3 \
-x_1-5,x_2 \
x_3 \
x_1-2,x_2+6,x_3
end{array}
right)
+ dots
$$
В разложении каждого элемента вектора отбросим все члены степени выше первой. В результате мы получили отображение, которое можно представить в матричном виде
$$
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) mapsto
underbrace{left(
begin{array}{r}
-14 \
2 \
-6 \
-33
end{array}
right)}_{=mathcal B}+
underbrace{left(
begin{array}{rrr}
2 & 0 & – 3 \
-1 & -5 & 0 \
0 & 0 & 1 \
1 & -2 & 6
end{array}
right)}_{=A}
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) .
$$
Это новое отображение является аффинным отображением пространства $ mathbb R^{3} $ в пространство $ mathbb R^{4} $. Таким образом, исходное, существенно нелинейное, отображение $ mathcal F(X) $ фактически заменили аффинным $ tilde{mathcal A}(X)=AX+mathcal B $. Насколько такая замена оправдана? — Ну, по крайней мере, в одной точке эти отображения совпадают: $ mathcal F(mathbb O) = tilde {mathcal A}(mathbb O) $. Трудно ожидать, что они будут совпадать еще где-нибудь. Однако же, в малой окрестности точки $ mathbb O $ значения этих двух функций оказываются близкими!
$$
begin{array}{lll}
mathcal F left(
begin{array}{r}
0.01 \
-0.02\
0.07
end{array}
right)=
left(
begin{array}{r}
-14.19000994 \
2.090000000 \
-5.930006860 \
-32.53000000
end{array}
right); &
mathcal F left(
begin{array}{r}
0.05 \
0.12\
-0.14
end{array}
right)=
left(
begin{array}{r}
-13.47907577 \
1.349999642 \
-6.140329280 \
-34.03000000
end{array}
right); & mathcal F left(
begin{array}{r}
-0.30 \
0.25\
-0.24
end{array}
right)=
left(
begin{array}{r}
-13.82475143 \
1.049938741 \
-6.243456000 \
-35.24000000
end{array}
right) ; dots
\
tilde{mathcal A}
left(
begin{array}{r}
0.01 \
-0.02\
0.07
end{array}
right)=
left(
begin{array}{r}
-14.19000000 \
2.090000000 \
-5.930000000 \
-32.53000000
end{array}
right) ; &
tilde{mathcal A}
left(
begin{array}{r}
0.05 \
0.12\
-0.14
end{array}
right)=
left(
begin{array}{r}
-13.48000000 \
1.350000000\
-6.140000000 \
-34.03000000
end{array}
right) &
tilde{mathcal A} left(
begin{array}{r}
-0.30 \
0.25\
-0.24
end{array}
right)=
left(
begin{array}{r}
-13.88000000 \ 1.050000000 \ -6.240000000 \ -35.24000000
end{array}
right); dots
end{array}
$$
Иными словами, в некоторой достаточно малой окрестности6) точки $ X_0=mathbb O_{} $ нелинейное отображение аппроксимируется аффинным. А чем аппроксимировать за пределами этой окрестности, скажем, в окрестности вектора $ X_0=[1,-1,1]^top $? — Для этого придется привлекать аппарат разложения нелинейных функций нескольких переменных в ряды Тейлора. К счастью, функции нашего примера являются полиномиальными, поэтому этот ряд не будет содержать бесконечного числа членов. Воспользовавшись материалом пункта
☞
ФОРМУЛА ТЕЙЛОРА, получим:
$$
mathcal F left(
begin{array}{r}
x_1 \
x_2\
x_3
end{array}
right)
=
left(
begin{array}{c}
-31-sqrt{2} \
9 \
-6 \
-24
end{array}
right)+
left(
begin{array}{rrr}
(6-2,sqrt{2})(x_1-1) &+ 85, (x_2+1) & +(-sqrt{2}-3)(x_3-1)\
&-34,(x_2+1) & +6,(x_3-1) \
&(x_2+1) & -2,(x_3-1)\
(x_1-1) &- 2,(x_2+1) & +6,(x_3-1)
end{array}
right)+ dots
$$
Перепишем второе слагаемое в матричном виде:
$$
=
left(
begin{array}{c}
-31-sqrt{2} \
9 \
-6 \
-24
end{array}
right)+
left(
begin{array}{ccc}
6-2,sqrt{2} &85& -sqrt{2}-3\
0 &-34 & 6 \
0&1& -2\
1 &- 2 & 6
end{array}
right)left(
begin{array}{c}
x_1-1 \
x_2+1 \
x_3-1
end{array}
right) + dots
$$
В общем же случае, если
$$
mathcal{F} left(
begin{array}{l}
x_1 \
x_2\
vdots \
x_n
end{array}
right)=
left(
begin{array}{c}
f_1(x_1,dots,x_n) \
vdots \
f_m(x_1,dots,x_n)
end{array}
right),
$$
то, в окрестности вектора $ X_0= (x_{01},x_{02},dots,x_{0n})^{top} $ его можно аппроксимировать аффинным отображением
$$
tilde{mathcal A} left(
begin{array}{l}
y_1 \
y_2\
vdots \
y_n
end{array}
right)=
underbrace{left(
begin{array}{c}
f_1(x_{01},dots,x_{0n}) \
vdots \
f_m(x_{01},dots,x_{0n})
end{array}
right)}_{=mathcal F(X_0)}+
underbrace{left(
begin{array}{cccc}
{partial f_1}/{partial x_1} & {partial f_1}/{partial x_2} & dots & {partial f_1}/{partial x_n} \
{partial f_2}/{partial x_1} & {partial f_2}/{partial x_2} & dots & {partial f_2}/{partial x_n} \
dots & && dots \
{partial f_m}/{partial x_1} & {partial f_m}/{partial x_2} & dots & {partial f_m}/{partial x_n}
end{array}
right)}_{mathbf J}left(
begin{array}{l}
y_1 \
y_2\
vdots \
y_n
end{array}
right) ,
$$
которое рассматривается в окрестности $ Y_0=mathbb O_{} $. Здесь все частные производные в матрице $ mathbf J $ вычисляются в точке $ X_{0} $. Матрица
$$
mathbf J = left[ frac{partial f_j}{partial x_k} right]_{j=1,dots,m, atop k=1,dots,n}
$$
называется матрицей Якоби системы из $ m_{} $ функций $ {f_1(x_1,dots,x_n),dots,f_m(x_{1},dots,x_n)} $ по переменным $ x_1,dots,x_{n} $. Линейное отображение
$$
mathbf J left(
begin{array}{l}
y_1 \
y_2\
vdots \
y_n
end{array}
right)
$$
известно как дифференциал (первого порядка) функции $ mathcal F(X) $ в точке $ X_0 $.
Подводя итог, можно сказать, что линейные (аффинные) отображения служат основой анализа отображений нелинейных — но этот анализ носит локальный характер: линеаризация адекватно приближает исходное нелинейное отображение лишь в малых областях значений аргументов.













![{displaystyle left[{begin{array}{ccc|c}2&3&5&0\-4&2&3&0end{array}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5714ae9767da1d68a8826f59d3f1df192764c1a7)
![{displaystyle left[{begin{array}{ccc|c}1&0&1/16&0\0&1&13/8&0end{array}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dd8ba9c851e7adfab7845d89e0f4620e56be52d)








![{displaystyle A=left[{begin{array}{cccccc}1&0&-3&0&2&-8\0&1&5&0&-1&4\0&0&0&1&7&-9\0&0&0&0&0&0end{array}},right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0972372a6a55ce6f1e89d59cd4c80db78f07eb0f)
![{displaystyle left[{begin{array}{c}A\hline Eend{array}}right]=left[{begin{array}{cccccc}1&0&-3&0&2&-8\0&1&5&0&-1&4\0&0&0&1&7&-9\0&0&0&0&0&0\hline 1&0&0&0&0&0\0&1&0&0&0&0\0&0&1&0&0&0\0&0&0&1&0&0\0&0&0&0&1&0\0&0&0&0&0&1end{array}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/952ce567a3c13d72611dfb429290701721434f5c)
![{displaystyle left[{begin{array}{c}B\hline Cend{array}}right]=left[{begin{array}{cccccc}1&0&0&0&0&0\0&1&0&0&0&0\0&0&1&0&0&0\0&0&0&0&0&0\hline 1&0&0&3&-2&8\0&1&0&-5&1&-4\0&0&0&1&0&0\0&0&1&0&-7&9\0&0&0&0&1&0\0&0&0&0&0&1end{array}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d12b3c06e06f4ea602e52aa23819eccc250e6ba4)
![{displaystyle left[!!{begin{array}{r}3\-5\1\0\0\0end{array}}right],;left[!!{begin{array}{r}-2\1\0\-7\1\0end{array}}right],;left[!!{begin{array}{r}8\-4\0\9\0\1end{array}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4475f0a687bbd8ed7c618b63795b4b4898daa755)
