Как найти базисные строки матрицы - Сайт, где вы сможете решить свои вопросы

1. Понятие линейной зависимости строк.
Выше говорилось о том, что строка

является линейной комбинацией строк

,

,
…,

,
если для некоторых вещественных чисел

справедливы
равенства:

. (1.4.1)

Равенства (1.4.1) (n равенств) можно
записать в виде одного матричного
равенства:

, (1.4.2)

понимая его в смысле n равенств
вида (1.4.1).

Определение 1. Строки матрицы

,…,

называются линейно зависимыми, если
существуют такие числа

,
хотя одно из которых не равно нулю, что
справедливы равенства

(1.4.3)

В сокращенном виде:

. (1.4.4)

Определение 2. Строки матрицы

,
…,

называются линейно независимыми, если
равенства (1.4.3) выполняются только в том
случае, когда все

/
(1.4.5)

Теорема 1.5. Для того, чтобы строки

были
линейно зависимы необходимо и достаточно,
чтобы одна из этих строк являлась
линейной комбинацией остальных строк.

Доказательство. 1) Необходимость.
Пусть строки

линейно зависимы. Тогда (по определению)
справедливо равенство:

.
(1.4.6)

при том, что не все

равны нулю. Пусть для определенности

.
Тогда имеем:

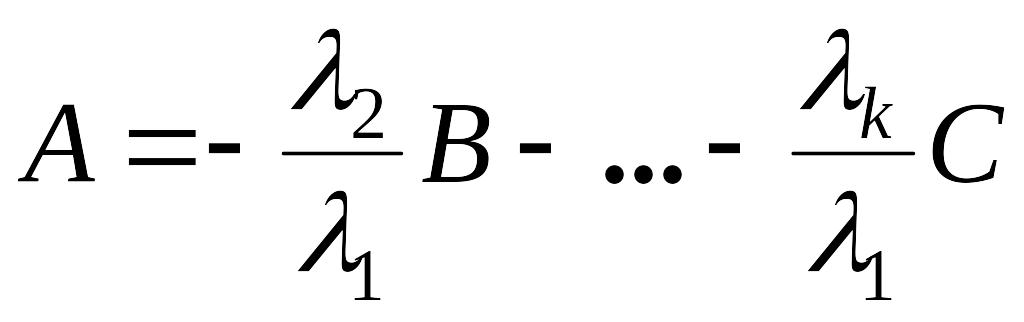
(1.4.7)

.
Откуда получаем:

, (1.4.8)

т.е.

является линейной комбинацией строк

2) Достаточность. Пусть

является линейной комбинацией строк

Тогда можно записать:

(1.4.9)

или

. (1.4.10)

Выполняется равенство (1.4.10.) при том,
что по крайней мере, один из коэффициентов
линейной комбинации

не равен нулю. Тогда, по определению,
строки

линейно зависимы. Теорема доказана.

Все приводимые выше рассуждения
справедливы не только для строк матрицы,
но и для её столбцов.

2. Теорема о базисном миноре.
Рассмотрим произвольную (не
обязательно квадратную матрицу)

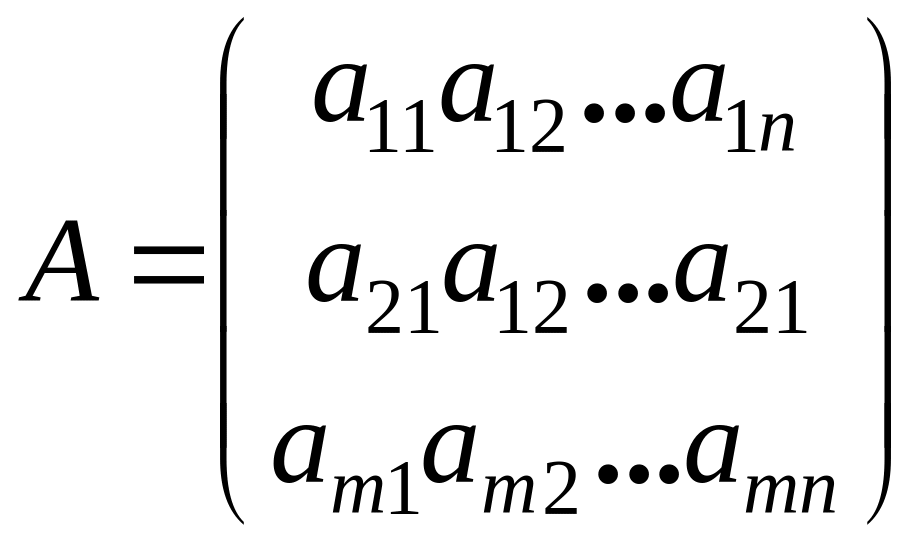
. (1.4.11)

Минором

-го
порядка матрицы

будем называть определитель

-го
порядка с элементами, стоящими на
пересечении любых

строк и

столбцов матрицы

.

Если хотя бы один из элементов

матрицы

отличен от нуля. Тогда найдется целое
положительное число

,
что будут выполняться следующие два
условия: у матрицы

имеется минор

-го
порядка, отличный от нуля; всякий минор

-го
и более высокого порядка (если такой
существует) равен нулю.

Определение 3. Минор матрицы

максимального порядка

,
отличный от нуля, называется базисным
минором матрицы.

Определение 4. Максимальный
порядок

отличного от нуля минора матрицы
называется рангом матрицы.

Столбцы и строки, на пересечении которых
стоит базисный минор матрицы, называются
базисными строками и базисными столбцами.
У матрицы порядка

,
где

существует
несколько миноров

-го
порядка, отличных от нуля, т.е. базисных
миноров.

Теорема 1.6 (о базисном миноре).
Базисные строки (базисные столбцы)
линейно независимы. Любая строка (любой
столбец) матрицы

_{является линейной комбинацией базисных

строк (базисных столбцов).}

Доказательство. Рассуждения
проводим для строк.Если бы базисные
строки были линейно зависимыми, то
определитель

-го
был бы равен нулю. Действительно, в
случае линейной зависимости базисных
строк, одна из них являлась бы линейной
комбинацией всех остальных. Но, если из
этой строки вычесть линейную комбинацию
других строк, величина определителя не
изменится. В тоже время появится строка,
состоящая из одних нулей, т.е. определитель
порядка

-базисный
минор равен нулю, что противоречит его
определению.

Докажем, что любая строка является
линейной комбинацией базисных строк
матрицы. Не ограничивая общности, будем
считать, что базисный минор находится
в левом верхнем углу матрицы. Пусть

.
Убедимся, что

-го порядка равен нулю.

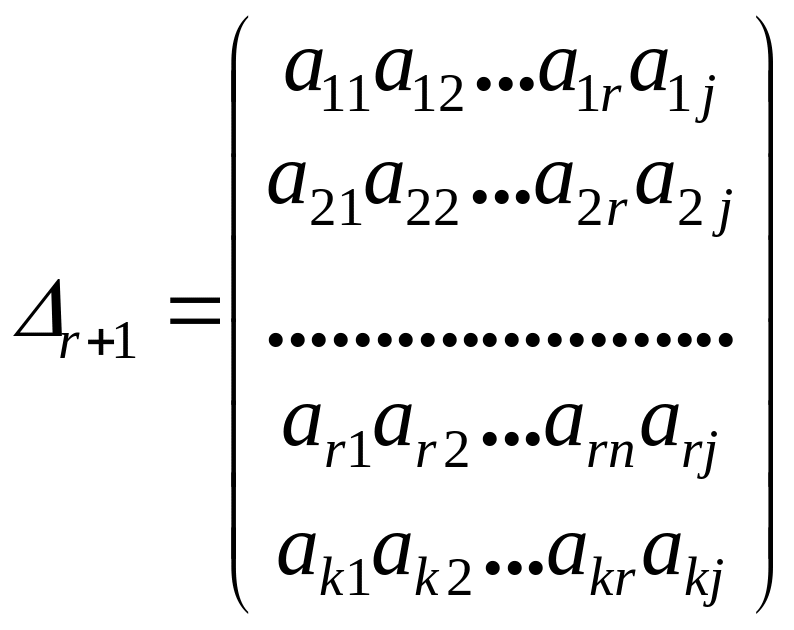
. (1.4.12)

Если

или
,
то определитель (1.4.12.) равен нулю в силу
того, что он имеет две одинаковые строки
или столбца. Если

и

,
то определитель (1.4.12.) является минором
матрицы

порядка, а всякий такой минор равен нулю
по определению базисного минора. Таким
образом:

при

.

Разложим определитель (1.4.12) по последнему
столбцу:

(1.4.13)

Алгебраические дополнения

элементов последнего столбца не зависят
от номера

.
Поэтому введем обозначение:

.
(1.4.14)

Учитывая (1.4.14.), формулу (1.4.13) перепишем
в виде:

.
(1.4.15)

Соотношение (1.4.15) справедливо для всех

.
Перепишем (1.4.15) в виде:

.
(1.4.16)

Окончательно получаем:

.
(1.4.17)

Соотношение (1.4.17) показывает, что любая

-ая
строка матрицы является линейной
комбинацией базисных строк. Теорема
доказана.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Вторая часть.

В первой части этой темы были подробно разобраны два примера. В этой части мы разберём ещё пару примеров, первый из которых решим несколько иным методом, чем примеры предыдущей части.

Пример №3

Решить СЛАУ $left{begin{aligned}
& 3x_1-x_2+2x_3=5;\
& -4x_1+7x_2-x_3=-3;\
& 2x_1+5x_2+3x_3=7.
end{aligned}right.$. Если система является неопределённой, указать базисное решение.

Решение

Найдём ранг матрицы системы и ранг расширенной матрицы системы с помощью метода окаймляющих миноров. Поработаем с расширенной матрицы системы:

$$
widetilde{A}=left(begin{array}{ccc|c}
3 & -1 & 2 & 5 \
-4 & 7 & -1 & -3 \
2 & 5 & 3 & 7 end{array}right)
$$

Начнём с миноров второго порядка. Возьмём минор матрицы, элементы которого расположены на пересечении строк №1, №2 и столбцов №1, №2:

$$
M_2=left|begin{array}{cc} 3 & -1 \ -4 & 7 end{array}right|=21-4=17.
$$

Этот минор второго порядка не равен нулю, поэтому начнем исследовать миноры третьего порядка, окаймляющие $M_2$. Есть два минора третьего порядка, окаймляющих данный минор второго порядка. Элементы первого из них, $M_{3}^{(1)}$ находятся на пересечении строк №1, №2, №3 и столбцов №1, №2, №3. Элементы второго окаймляющего минора третьего порядка, $M_{3}^{(2)}$, находятся на пересечении строк №1, №2, №3 и столбцов №1, №2, №4. Вычислим эти миноры:

$$
M_{3}^{(1)}=left|begin{array}{ccc}
3 & -1 & 2 \
-4 & 7 & -1 \
2 & 5 & 3 end{array}right|=0; ;

M_{3}^{(2)}=left|begin{array}{ccc}
3 & -1 & 5 \
-4 & 7 & -3 \
2 & 5 & 7 end{array}right|=0.
$$

Оба окаймляющих минора равны нулю, а последний ненулевой минор был второго порядка. Вывод: $rangwidetilde{A}=2$, а минор $M_2$ – базисный минор матрицы $widetilde{A}$. Теперь рассмотрим матрицу системы, т.е.
$A=left(begin{array}{ccc}
3 & -1 & 2\
-4 & 7 & -1\
2 & 5 & 3end{array}right)$. Минор $M_2$, который мы рассматривали для матрицы $widetilde{A}$, является также минором второго порядка матрицы $A$. Минор $M_{3}^{(1)}$ совпадает с определителем матрицы $A$, при этом $M_{3}^{(1)}=0$ . Иных миноров третьего порядка у матрицы $A$ нет. Итак, последний ненулевой минор матрицы $A$ был второго порядка. Вывод: $rang A=2$, а минор $M_2$ – базисный минор матрицы $A$. Так как ранги матрицы системы и расширенной матрицы системы равны между собой, но меньше нежели количество неизвестных (т.е. меньше, чем 3), то согласно следствию из теоремы Кронекера-Капелли данная система является неопределённой (т.е. имеет бесконечное количество решений).

Итак, ранги равны между собой и равны $r=2$, количество переменных $n=3$. Вывод: надо выбрать 2 базисных переменных и $n-r=1$ свободную переменную.

Минор $M_2$, элементы которого находятся в столбцах №1 и №2, является базисным минором матрицы $A$. Столбцы №1 и №2 соответствуют переменным $x_1$ и $x_2$. Свободной переменной, соответственно, будет $x_3$. Кроме того, элементы базисного минора $M_2$ находятся в строках №1 и №2. Именно эти строки СЛАУ мы и оставим, а третью строку уберём:

$$
left{begin{aligned}
& 3x_1-x_2+2x_3=5;\
& -4x_1+7x_2-x_3=-3.
end{aligned}right.
$$

Перебросим свободную переменную, т.е. $x_3$, в правые части обоих уравнений:

$$
left{begin{aligned}
& 3x_1-x_2=5-2x_3;\
& -4x_1+7x_2=-3+x_3.
end{aligned}right.
$$

А теперь решим эту систему методом Крамера:

$$
Delta=left|begin{array}{cc} 3 & -1 \ -4 & 7 end{array}right|=17;;
Delta_{x_1}=left|begin{array}{cc} 5-2x_3 & -1 \ -3+x_3 & 7 end{array}right|=32-13x_3;;
Delta_{x_2}=left|begin{array}{cc} 3 & 5-2x_3 \ -4 & -3+x_3 end{array}right|=11-5x_3.\
x_1=frac{Delta_{x_1}}{Delta}=frac{32-13x_3}{17}=frac{32}{17}-frac{13}{17}x_3;;
x_2=frac{Delta_{x_2}}{Delta}=frac{11-5x_3}{17}=frac{11}{17}-frac{5}{17}x_3.
$$

Итак, общее решение: $left{begin{aligned}
& x_1=frac{32}{17}-frac{13}{17}x_3;\
& x_2=frac{11}{17}-frac{5}{17}x_3;\
& x_3 in R.
end{aligned}right.$. Чтобы найти базисное решение, свободную переменную приравняем к нулю: $x_3=0$. Базисное решение будет таким:

$$
left{begin{aligned}
& x_1=frac{32}{17};\
& x_2=frac{11}{17};\
& x_3=0.
end{aligned}right.
$$

Ответ: Общее решение: $left{begin{aligned}
& x_1=frac{32}{17}-frac{13}{17}x_3;\
& x_2=frac{11}{17}-frac{5}{17}x_3;\
& x_3 in R.
end{aligned}right.$, базисное решение: $left{begin{aligned}
& x_1=frac{32}{17};\
& x_2=frac{11}{17};\
& x_3=0.
end{aligned}right.$.

Пример №4

Решить СЛАУ

$$left{begin{aligned}
& x_1-2x_2+3x_3+4x_5=-5;\
& 2x_1+x_2+5x_3+2x_4+9x_5=-3;\
& 3x_1+4x_2+7x_3+4x_4+14x_5=-1;\
& 2x_1-4x_2+6x_3+11x_5=2;\
& -2x_1+14x_2-8x_3+4x_4-7x_5=20;\
& -4x_1-7x_2-9x_3-6x_4-21x_5=-9.
end{aligned}right.$$

Если система является неопределённой, указать базисное решение.

Решение

Точно так же, как и в примерах предыдущей части, применим метод Гаусса:

$$
left(begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\
2 & 1 & 5 & 2 & 9 & -3\
3 & 4 & 7 & 4 & 14 & -1\
2 & -4 & 6 & 0 & 11 & 2\
-2 & 14 & -8 & 4 & -7 & 20\
-4 & -7 & -9 & -6 & -21 & -9 end{array}right)
begin{array} {l} phantom{0} \r_2-2r_1 \r_3-3r_1\r_4-2r_1\ r_5+2r_1\r_6+4r_1 end{array} rightarrow

left(begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\
0 & 5 & -1 & 2 & 1 & 7\
0 & 10 & -2 & 4 & 2 & 14\
0 & 0 & 0 & 0 & 3 & 12\
0 & 10 & -2 & 4 & 1 & 10\
0 & -15 & 3 & -6 & -5 & -29 end{array}right)
begin{array} {l} phantom{0} \ phantom{0}\r_3-2r_2\1/3cdot{r_4}\r_5-2r_2\r_6+3r_2 end{array} rightarrow \

rightarrowleft(begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\
0 & 5 & -1 & 2 & 1 & 7\
0 & 0 & 0 & 0 & 0 & 0\
0 & 0 & 0 & 0 & 1 & 4\
0 & 0 & 0 & 0 & -1 & -4\
0 & 0 & 0 & 0 & -2 & -8 end{array}right)
$$

Нулевую третью строку вычеркнем, а потом продолжим решение методом Гаусса:

$$
left(begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\
0 & 5 & -1 & 2 & 1 & 7\
0 & 0 & 0 & 0 & 1 & 4\
0 & 0 & 0 & 0 & -1 & -4\
0 & 0 & 0 & 0 & -2 & -8 end{array}right)
begin{array} {l} phantom{0} \ phantom{0}\ phantom{0}\ r_4+r_3\ r_5+2r_3 end{array} rightarrow

left(begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\
0 & 5 & -1 & 2 & 1 & 7\
0 & 0 & 0 & 0 & 1 & 4\
0 & 0 & 0 & 0 & 0 & 0\
0 & 0 & 0 & 0 & 0 & 0end{array}right)
$$

Мы привели матрицу системы и расширенную матрицу системы к ступенчатому виду. Ранги обеих матриц равны $r=3$, т.е. надо выбрать 3 базисных переменных. Количество неизвестных $n=5$, поэтому нужно выбрать $n-r=2$ свободных переменных. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли данная система является неопределённой (т.е. имеет бесконечное количество решений). Для нахождения решений системы вновь составим “ступеньки”:

На “ступеньках” стоят элементы из столбцов №1, №2, №5. Следовательно, базисными будут переменные $x_1$, $x_2$, $x_5$. Свободными переменными, соответственно, будут $x_3$, $x_4$. Столбцы №3 и №4, соответствующие свободным переменным, перенесём за черту, при этом, конечно, не забыв сменить им знаки. Нулевые строки уберём и продолжим обратный ход метода Гаусса. Матрица до черты должна стать единичной.

$$
left(begin{array}{ccc|ccc}
1 & -2 & 4 & -5 & -3 & 0\
0 & 5 & 1 & 7 & 1 & -2\
0 & 0 & 1 & 4 & 0 & 0end{array}right)
begin{array} {l} r_1-4r_3 \ r_2-r_3\ phantom{0}end{array} rightarrow

left(begin{array}{ccc|ccc}
1 & -2 & 0 & -21 & -3 & 0\
0 & 5 & 0 & 3 & 1 & -2\
0 & 0 & 1 & 4 & 0 & 0end{array}right)
begin{array} {l} phantom{0} \ 1/5cdot{r_2}\ phantom{0}end{array} rightarrow\

rightarrowleft(begin{array}{ccc|ccc}
1 & -2 & 0 & -21 & -3 & 0\
0 & 1 & 0 & 3/5 & 1/5 & -2/5\
0 & 0 & 1 & 4 & 0 & 0end{array}right)
begin{array} {l} r_1+2r_2 \ phantom{0}\ phantom{0}end{array} rightarrow

left(begin{array}{ccc|ccc}
1 & 0 & 0 & -99/5 & -13/5 & -4/5\
0 & 1 & 0 & 3/5 & 1/5 & -2/5\
0 & 0 & 1 & 4 & 0 & 0end{array}right).
$$

Из последней матрицы получим общее решение: $left{begin{aligned}
& x_1=-frac{99}{5}-frac{13}{5}x_3-frac{4}{5}x_4;\
& x_2=frac{3}{5}+frac{1}{5}x_3-frac{2}{5}x_4;\
& x_3 in R;\
& x_4in R;\
& x_5=4.
end{aligned}right.$. Базисное решение найдём, приняв свободные переменные равными нулю, т.е. $x_3=0$, $x_4=0$:

$$
left{begin{aligned}
& x_1=-frac{99}{5};\
& x_2=frac{3}{5};\
& x_3=0;\
& x_4=0;\
& x_5=4.
end{aligned}right.
$$

Задача решена, осталось лишь записать ответ.

Ответ: Общее решение: $left{begin{aligned}
& x_1=-frac{99}{5}-frac{13}{5}x_3-frac{4}{5}x_4;\
& x_2=frac{3}{5}+frac{1}{5}x_3-frac{2}{5}x_4;\
& x_3 in R;\
& x_4in R;\
& x_5=4.
end{aligned}right.$, базисное решение: $left{begin{aligned}
& x_1=-frac{99}{5};\
& x_2=frac{3}{5};\
& x_3=0;\
& x_4=0;\
& x_5=4.
end{aligned}right.$.

Источник

Среди миноров матрицы могут быть как равные нулю, так и отличные от нуля.

Определение 12.4. Минор М матрицы A называют базисным, если выполнены два условия:

а) он не равен нулю;

б) его порядок равен рангу матрицы A.

Матрица A может иметь несколько базисных миноров. Строки и столбцы матрицы A, в которых расположен выбранный базисный минор, называют базисными.

Следующую теорему, занимающую одно из центральных мест в теории матриц и ее прило-жениях, называют теоремой о базисном миноре.

Теорема 12.5. Базисные строки (столбцы) матрицы A, соответствующие любому ее базисному минору M, линейно независимы. Любые строки (столбцы) матрицы A, не входящие в М, являются линейными комбинациями базисных строк (столбцов).

◄ Доказательство проведем для строк. Пусть ранг матрицы A = (a_ij) типа m × n равен r. Фиксируем какой-либо ее базисный минор M и соответствующие ему базисные строки матрицы A.

Докажем, что базисные строки линейно независимы. Предположим, что они линейно зависимы. Тогда по теореме 12.3 одна из них является линейной комбинацией остальных базисных строк. Согласно свойствам определителей, минор M равен нулю. Это противоречит тому, что минор M базисный.

Теперь докажем, что любая строка матрицы A, не входящая в базисный минор, является линейной комбинацией базисных строк. Предположим, не ограничивая общности доказательства, что базисный минор M расположен в верхнем левом углу матрицы. Пусть i — номер строки, не являющейся базисной, т.е. r + 1 ≤ i ≤ m. Покажем, что определитель порядка r + 1

полученный добавлением к минору M элементов i-й строки и произвольного j-го столбца матрицы A, j = 1,n, равен нулю. При j ≤ r определитель равен нулю, так как он содержит два одинаковых столбца. Если же j > r, то Δ = 0, так как в этом случае Δ является минором матрицы A, порядок которого равен r + 1 и больше ранга матрицы. Итак, Δ = 0.

Раскладывая определитель Δ по последнему столбцу, получаем равенство

A_{1,r + 1}a_1j + A_{2,r + 1}a_2j + … + A_{r,r + 1}a_rj + A_{r + 1,r + 1}a_2ij — 0,

в котором через A_{1,r + 1}, A_{2,r + 1}, …, A_{r,r + 1}, A_{r + 1,r + 1} обозначены алгебраические дополнения соответствующих элементов рассматриваемого определителя. Отметим, что эти алгебраические дополнения не зависят от номера j, т.е. не зависят от того, элементы какого из столбцов матрицы A взяты в качестве последнего столбца определителя Δ. Кроме того, A_{r + 1,r + 1} = M ≠ 0. Поэтому из последнего равенства следует, что для всех j = 1,n

a_ij = b₁a_1j + b₂a_2j + … + b_ra_rj,

где коэффициенты b_k = – A_k,r+1/A_r+1,r+1, k = _1,r, не зависят от j, а это означает, что i-я строка (г + 1 ≤ i ≤ m) матрицы A является линейной комбинацией первых г ее строк, т.е. линейной комбинацией ее базисных строк. ►

Следствие 12.1. Для того чтобы квадратная матрица была невырожденной, необходимо и достаточно, чтобы ее строки (столбцы) были линейно независимы.

◄ Необходимость. Если квадратная матрица A невырождена, то ее ранг равен ее порядку, а ее определитель является базисным минором. Поэтому все строки (столбцы) являются базисными и по теореме 12.5 о базисном миноре они линейно независимы.

Достаточность. Если все строки (столбцы) квадратной матрицы A являются линейно независимыми, то они являются базисными. Действительно, если бы только некоторые из них были базисными, то, согласно теореме 12.5 о базисном миноре, оставшиеся были бы линейными комбинациями базисных и, следовательно, строки (столбцы) матрицы A, согласно теореме 12.4, были бы линейно зависимыми. Так как все строки и столбцы квадратной матрицы A являются базисными, а им соответствует определитель матрицы, то он является базисным минором и, следовательно, согласно определению 12.4, отличен от нуля, т.е. квадратная матрица A невырождена. ►

Теорема 12.6. Линейно независимые строки (столбцы) матрицы, количество которых равно рангу матрицы, являются базисными строками (столбцами).

◄ Докажем теорему для строк. Зафиксируем произвольный набор из r линейно независимых строк матрицы, где r — это ранг матрицы. Нам достаточно показать, что хотя бы один из базисных миноров расположен в фиксированных строках. Отбросим остальные строки матрицы и докажем, что ранг новой матрицы, содержащей r строк, равен r. Так как новая матрица не имеет миноров порядка больше чем r, то ее ранг не может превосходить r. Если бы он был меньше r, то только часть этих r фиксированных строк были бы базисными в новой матрице, а остальные, согласно теореме 12.5 о базисном миноре, являлись бы их линейными комбинациями. Согласно теореме 12.4, последнее означало бы линейную зависимость фиксированных г строк, что противоречит условию теоремы.

Итак, ранг новой матрицы равен r. Ее базисный минор имеет порядок r и является ненулевым минором порядка r исходной матрицы, расположенным в рассмотренных фиксированных r строках. ►

Теорема 12.7 (Теорема о ранге матрицы). Для любой матрицы ее ранг равен максимальному количеству ее линейно независимых строк (столбцов).

◄ Доказательство теоремы проведем для строк. Согласно теореме 12.5 о базисном миноре, базисные строки линейно независимы. Следовательно, максимальное количество k линейно независимых строк матрицы не может быть меньше ранга г матрицы. Итак, k ≥ r.

Остается доказать, что k ≤ r. Отбросим те строки матрицы, которые не входят в число рассматриваемых k линейно независмых строк. Получим матрицу, в которой все k строк линейно независимы. Согласно теореме 12.6, все k строк этой матрицы являются базисными, а ее ранг равен k. Базисный минор матрицы из k строк имеет порядок k и является ненулевым минором порядка k исходной матрицы. Следовательно, k ≤ r. ►

Следствие 12.2. Для любой матрицы максимальное число линейно независимых строк равно максимальному числу линейно независимых столбцов.

Источник

Определение 1: Ранг матрицы – это число её линейно независимых строк.

Рассмотрим минор порядка R:

Матрицы А .

Определение 2: Рангом матрицы называется наивысший порядок минора матрицы, отличный от нуля.

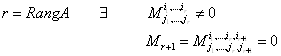
Теорема 5(о базисном миноре):

1. Тот минор , такой, что называется базисным. Строки и столбцы в базисном миноре называются базисными.

Теорема 5:

1) Базисные строки линейно независимы.

2) Любая строка матрицы является линейной комбинацией базисных строк.

Доказательство 1: Предположим, что базисные строки линейно зависимы, тогда по теореме 4 одна из строк является линейной комбинацией остальных. Но так как , а это базисный минор, то вычитая из данной строки эту линейную комбинацию, получаем нулевую строку, следовательно , следовательно базисные строки линейно независимы.

Доказательство 2:

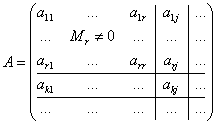
Рассмотрим ;

Строка есть линейная комбинация базисных строк.

Свойства :

3) , если

Доказательство первого утверждения(свойства):

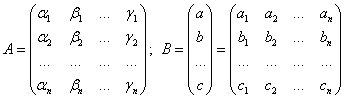
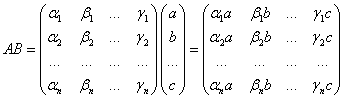
N строк линейно независимы

Так как в мы получаем N линейно независимых комбинаций строк , то очевидно, что число независимых строк возрастёт.

Доказательство 3-го утверждения(свойства):

Если , то из первого утверждения: , а из второго утверждения , значит

Элементарные преобразования:

1) Перестановка строк

2) Умножение строки на любое число, не равное нулю

3) Прибавление к элементам данной строки элементов других строк, умноженных на любое число.

Свойство: при элементарных преобразованиях ранг матрицы не меняется.

Теорема 6: Для того, чтобы , необходимо и достаточно, чтобы её строки были линейно независимы.

Доказательство (необходимость): Если , то строки линейно независимы. Так как , то среди строк имеется число линейно независимых строк, следовательно, совокупность всех строк является линейно независимой системой.

Доказательство (достаточность): Если строки линейно зависимы, то . Действительно, так как строки линейно зависимы, то одна из них есть линейная комбинация остальных. Тогда вычитая из этой строки данную линейную комбинацию, мы получаем нулевую строку, следовательно, .

Линейное пространство.

Рассмотрим множество L, произвольной природы.

Рассмотрим две операции элементов из L:

Определение: Множество называется линейным пространством, если в нём определены две операции – сложение и умножение и выполняется 8 аксиом(основных свойств):

Линейное пространство над полем вещественных, комплексных чисел определяет соответственно вещественное или комплексное линейное пространство.

Линейное пространство является также и группой.

Примеры:

1) – множество является линейный пространством при введении операций сложения и умножения.

R – группа относительно операции сложения.

– группа относительно операции умножения

3) – множество матриц порядка

4) – множество полиномов степени не выше, чем .

5) – множество функций, определённых и непрерывных на отрезке .

6) – нуль мерное пространство

Линейная зависимость

Пусть L – линейное пространство

– линейная комбинация векторов

– вектор есть линейная комбинация векторов.

Определение: система векторов называется линейно независимой, если их нулевая линейная комбинация выполняется только при . Если же среди существуют ненулевые элементы, то система линейно зависима.

Теорема 7: Для того, чтобы система была линейно зависимой, необходимо и достаточно, чтобы один из них линейно выражался через остальные(аналог теоремы 4).

< Предыдущая		Следующая >

Источник

Ранг матрицы и базисный минор матрицы

Пусть — матрица размеров mtimes n , а — натуральное число, не превосходящее и : kleqslantmin{m;n} . Минором k-го порядка матрицы называется определитель матрицы k-го порядка, образованной элементами, стоящими на пересечении произвольно выбранных строк и столбцов матрицы . Обозначая миноры, номера выбранных строк будем указывать верхними индексами, а выбранных столбцов — нижними, располагая их по возрастанию.

Пример 3.4. Записать миноры разных порядков матрицы

$A=begin{pmatrix}1&2&1&0\ 0&2&2&3\ 1&4&3&3end{pmatrix}!.$

Решение. Матрица имеет размеры 3times4 . Она имеет: 12 миноров 1-го порядка, например, минор $M_{2}^{3}=det(a_{32})=4$ ; 18 миноров 2-го порядка, например, $M_{23}^{12}=begin{vmatrix}2&1\2&2end{vmatrix}=2$ ; 4 минора 3-го порядка, например,

$M_{{134}}^{{123}}= begin{vmatrix}1&1&0\0&2&3\ 1&3&3 end{vmatrix}=0.$

В матрице размеров mtimes n минор r-го порядка называется базисным, если он отличен от нуля, а все миноры (r+1)-ro порядка равны нулю или их вообще не существует.

Рангом матрицы называется порядок базисного минора. В нулевой матрице базисного минора нет. Поэтому ранг нулевой матрицы, по определению полагают равным нулю. Ранг матрицы обозначается operatorname{rg}A .

Пример 3.5. Найти все базисные миноры и ранг матрицы

$A=begin{pmatrix}1&2&2&0\0&2&2&3\0&0&0&0end{pmatrix}!.$

Решение. Все миноры третьего порядка данной матрицы равны нулю, так как у этих определителей третья строка нулевая. Поэтому базисным может быть только минор второго порядка, расположенный в первых двух строках матрицы. Перебирая 6 возможных миноров, отбираем отличные от нуля

$M_{12}^{12}= M_{13}^{12}= begin{vmatrix}1&2\0&2 end{vmatrix}!,quad M_{24}^{12}= M_{34}^{12}= begin{vmatrix}2&0\2&3end{vmatrix}!,quad M_{14}^{12}= begin{vmatrix}1&0\0&3end{vmatrix}!.$

Каждый из этих пяти миноров является базисным. Следовательно, ранг матрицы равен 2.

Замечания 3.2

1. Если в матрице все миноры k-го порядка равны нулю, то равны нулю и миноры более высокого порядка. Действительно, раскладывая минор (k+1)-ro порядка по любой строке, получаем сумму произведений элементов этой строки на миноры k-го порядка, а они равны нулю.

2. Ранг матрицы равен наибольшему порядку отличного от нуля минора этой матрицы.

3. Если квадратная матрица невырожденная, то ее ранг равен ее порядку. Если квадратная матрица вырожденная, то ее ранг меньше ее порядка.

4. Для ранга применяются также обозначения operatorname{Rg}A,~ operatorname{rang}A,~ operatorname{rank}A .

5. Ранг блочной матрицы определяется как ранг обычной (числовой) матрицы, т.е. не обращая внимания на ее блочную структуру. При этом ранг блочной матрицы не меньше рангов ее блоков: operatorname{rg}(Amid B)geqslantoperatorname{rg}A и , поскольку все миноры матрицы (или ) являются также минорами блочной матрицы .

Теоремы о базисном миноре и о ранге матрицы

Рассмотрим основные теоремы, выражающие свойства линейной зависимости и линейной независимости столбцов (строк) матрицы.

Теорема 3.1 о базисном миноре. В произвольной матрице каждый столбец {строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.

Действительно, без ограничения общности предполагаем, что в матрице размеров mtimes n базисный минор расположен в первых строках и первых столбцах. Рассмотрим определитель

$D=left|begin{array}{ccc|c}a_{11}&cdots&a_{1r}&a_{1k}~\ ~vdots&ddots &vdots&vdots~\ ~a_{r1}&cdots&a_{rr}&a_{rk}~\hline ~a_{s1}&cdots&a_{sr}&a_{sk}end{array}right|,$

который получен приписыванием к базисному минору матрицы соответствующих элементов s-й строки и k-го столбца. Отметим, что при любых 1leqslant sleqslant m и 1leqslant kleqslant n этот определитель равен нулю. Если sleqslant r или kleqslant r , то определитель содержит две одинаковых строки или два одинаковых столбца. Если же s>r и k>r , то определитель равен нулю, так как является минором (r+l)-ro порядка. Раскладывая определитель по последней строке, получаем

$a_{s1}cdot D_{r+11}+ldots+ a_{sr}cdot D_{r+1r}+a_{sk}cdot D_{r+1,r+1}=0,$

где $D_{r+1,j}$ — алгебраические дополнения элементов последней строки. Заметим, что $D_{r+1,r+1}ne0$ , так как это базисный минор. Поэтому

$a_{sk}=lambda_1cdot a_{s1}+ldots+lambda_rcdot a_{sr}$ , где $lambda_j=-frac{D_{r+1,j}}{D_{r+1,r+1}},~j=1,2,ldots,r.$

Записывая последнее равенство для s=1,2,ldots,m , получаем

$begin{pmatrix}a_{1k}\vdots\a_{mk}end{pmatrix}= lambda_1cdot! begin{pmatrix}a_{11}\vdots\a_{m1}end{pmatrix}+ldots lambda_rcdot! begin{pmatrix}a_{1r}\vdots\a_{mr}end{pmatrix}!.$

т.е. -й столбец (при любом 1leqslant kleqslant n ) есть линейная комбинация столбцов базисного минора, что и требовалось доказать.

Теорема о базисном миноре служит для доказательства следующих важных теорем.

Условие равенства нулю определителя

Теорема 3.2 (необходимое и достаточное условие равенства нулю определителя). Для того чтобы определитель был равен нулю необходимо и достаточно, чтобы один из его столбцов {одна из его строк) был линейной комбинацией остальных столбцов (строк).

В самом деле, необходимость следует из теоремы о базисном миноре. Если определитель квадратной матрицы n-го порядка равен нулю, то ее ранг меньше , т.е. хотя бы один столбец не входит в базисный минор. Тогда этот выбранный столбец по теореме 3.1 является линейной комбинацией столбцов, в которых расположен базисный минор. Добавляя, при необходимости, к этой комбинации другие столбцы с нулевыми коэффициентами, получаем, что выбранный столбец есть линейная комбинация остальных столбцов матрицы. Достаточность следует из свойств определителя. Если, например, последний столбец A_n определителя det(A_1~A_2~cdots~A_n) линейно выражается через остальные

$A_n=lambda_1cdot A_1+lambda_2cdot A_2+ldots+lambda_{n-1}cdot A_{n-1},$

то прибавляя к A_n столбец A_1 , умноженный на (-lambda_1) , затем столбец A_2 , умноженный на (-lambda_2) , и т.д. столбец $A_{n-1}$ , умноженный на $(-lambda_{n-1})$ , получим определитель $det(A_1~cdots~A_{n-1}~o)$ с нулевым столбцом, который равен нулю (свойство 2 определителя).

Инвариантность ранга матрицы при элементарных преобразованиях

Теорема 3.3 (об инвариантности ранга при элементарных преобразованиях). При элементарных преобразованиях столбцов (строк) матрицы ее ранг не меняется.

Действительно, пусть operatorname{rg}A=r . Предположим, что в результате одного элементарного преобразования столбцов матрицы получили матрицу . Если было выполнено преобразование I типа (перестановка двух столбцов), то любой минор (r+l)-ro порядка матрицы либо равен соответствующему минору (r+l)-ro порядка матрицы , либо отличается от него знаком (свойство 3 определителя). Если было выполнено преобразование II типа (умножение столбца на число lambdane0 ), то любой минор (г+l)-ro порядка матрицы либо равен соответствующему минору (r+l)-ro порядка матрицы , либо отличается от него множителем (свойство 6 определителя). Если было выполнено преобразование III типа (прибавление к одному столбцу другого столбца, умноженного на число Lambda ), то любой минор (г+1)-го порядка матрицы либо равен соответствующему минору (г+1) -го порядка матрицы (свойство 9 определителя), либо равен сумме двух миноров (r+l)-ro порядка матрицы (свойство 8 определителя). Поэтому при элементарном преобразовании любого типа все миноры (r+l)-ro порядка матрицы равны нулю, так как равны нулю все миноры (г+l)-ro порядка матрицы . Таким образом, доказано, что при элементарных преобразованиях столбцов ранг матрицы не может увеличиться. Так как преобразования, обратные к элементарным, являются элементарными, то ранг матрицы при элементарных преобразованиях столбцов не может и уменьшиться, т.е. не изменяется. Аналогично доказывается, что ранг матрицы не изменяется при элементарных преобразованиях строк.

Следствие 1. Если одна строка (столбец) матрицы является линейной комбинацией других ее строк (столбцов), то эту строку (столбец) можно вычеркнуть из матрицы, не изменив при этом ее ранга.

Действительно, такую строку при помощи элементарных преобразований можно сделать нулевой, а нулевая строка не может входить в базисный минор.

Следствие 2. Если матрица приведена к простейшему виду (1.7), то

operatorname{rg}A=operatorname{rg}Lambda=r,.

Действительно, матрица простейшего вида (1.7) имеет базисный минор r-го порядка.

Следствие 3. Любая невырожденная квадратная матрица является элементарной, другими словами, любая невырожденная квадратная матрица эквивалентна единичной матрице того же порядка.

Действительно, если — невырожденная квадратная матрица n-го порядка, то operatorname{rg}A=n (см. п.З замечаний 3.2). Поэтому, приводя элементарными преобразованиями матрицу к простейшему виду (1.7), получим единичную матрицу Lambda=E_n , так как operatorname{rg}A=operatorname{rg}Lambda=n (см. следствие 2). Следовательно, матрица эквивалентна единичной матрице E_n и может быть получена из нее в результате конечного числа элементарных преобразований. Это означает, что матрица элементарная.

Теорема 3.4 (о ранге матрицы). Ранг матрицы равен максимальному числу линейно независимых строк этой матрицы.

В самом деле, пусть operatorname{rg}A=r . Тогда в матрице имеется линейно независимых строк. Это строки, в которых расположен базисный минор. Если бы они были линейно зависимы, то этот минор был бы равен нулю по теореме 3.2, а ранг матрицы не равнялся бы . Покажем, что — максимальное число линейно независимых строк, т.е. любые строк линейно зависимы при p>r . Действительно, образуем из этих строк матрицу . Поскольку матрица — это часть матрицы , то operatorname{rg}Bleqslant operatorname{rg}A=r<p . Значит, хотя бы одна строка матрицы не входит в базисный минор этой матрицы. Тогда по теореме о базисном миноре она равна линейной комбинации строк, в которых расположен базисный минор. Следовательно, строки матрицы линейно зависимы. Таким образом, в матрице не более, чем линейно независимых строк.

Следствие 1. Максимальное число линейно независимых строк в матрице равно максимальному числу линейно независимых столбцов:

$operatorname{rg}A=operatorname{rg}A^T.$

Это утверждение вытекает из теоремы 3.4, если ее применить к строкам транспонированной матрицы и учесть, что при транспонировании миноры не изменяются (свойство 1 определителя).

Следствие 2. При элементарных преобразованиях строк матрицы линейная зависимость (или линейная независимость) любой системы столбцов этой матрицы сохраняется.

В самом деле, выберем любые столбцов данной матрицы и составим из них матрицу . Пусть в результате элементарных преобразований строк матрицы была получена матрица , а в результате тех же преобразований строк матрицы была получена матрица . По теореме 3.3 operatorname{rg}B'=operatorname{rg}B . Следовательно, если столбцы матрицы были линейно независимы, т.е. k=operatorname{rg}B (см. следствие 1), то и столбцы матрицы также линейно независимы, так как k=operatorname{rg}B' . Если столбцы матрицы были линейно зависимы (k>operatorname{rg}B) , то и столбцы матрицы также линейно зависимы (k>operatorname{rg}B') . Следовательно, для любых столбцов матрицы линейная зависимость или линейная независимость сохраняется при элементарных преобразованиях строк.

Замечания 3.3

1. В силу следствия 1 теоремы 3.4 свойство столбцов, указанное в следствии 2, справедливо и для любой системы строк матрицы, если элементарные преобразования выполняются только над ее столбцами.

2. Следствие 3 теоремы 3.3 можно уточнить следующим образом: любую невырожденную квадратную матрицу, используя элементарные преобразования только ее строк (либо только ее столбцов), можно привести к единичной матрице того же порядка.

В самом деле, используя только элементарные преобразования строк, любую матрицу можно привести к упрощенному виду Lambda (рис. 1.5) (см. теорему 1.1). Поскольку матрица невырожденная (det{A}ne0) , то ее столбцы линейно независимы. Значит, столбцы матрицы Lambda также линейно независимы (следствие 2 теоремы 3.4). Поэтому упрощенный вид Lambda невырожденной матрицы совпадает с ее простейшим видом (рис. 1.6) и представляет собой единичную матрицу Lambda=E (см. следствие 3 теоремы 3.3). Таким образом, преобразовывая только строки невырожденной матрицы, ее можно привести к единичной. Аналогичные рассуждения справедливы и для элементарных преобразований столбцов невырожденной матрицы.

Ранге произведения и суммы матриц

Теорема 3.5 (о ранге произведения матриц). Ранг произведения матриц не превышает ранга множителей:

operatorname{rg}(Acdot B)leqslant min{operatorname{rg}A,operatorname{rg}B}.

В самом деле, пусть матрицы и имеют размеры mtimes p и ptimes n . Припишем к матрице матрицу C=ABcolon,(Amid C) . Разумеется, что operatorname{rg}Cleqslantoperatorname{rg}(Amid C) , так как — это часть матрицы (см. п.5 замечаний 3.2). Заметим, что каждый столбец C_j , согласно операции умножения матриц, является линейной комбинацией столбцов A_1,A_2,ldots,A_p матрицы A=(A_1~cdots~A_p):

$C_{j}=A_1cdot b_{1j}+A_2cdot b_{2j}+ldots+A_{p}cdot b_{pj},quad j=1,2,ldots,n.$

Такой столбец можно вычеркнуть из матрицы (Amid C) , при этом ее ранг не изменится (следствие 1 теоремы 3.3). Вычеркивая все столбцы матрицы , получаем: operatorname{rg}(Amid C)=operatorname{rg}A . Отсюда, operatorname{rg}Cleqslantoperatorname{rg}(Amid C)=operatorname{rg}A . Аналогично можно доказать, что одновременно выполняется условие , и сделать вывод о справедливости теоремы.

Следствие. Если невырожденная квадратная матрица, то operatorname{rg}(AB)= operatorname{rg}B и operatorname{rg}(CA)=operatorname{rg}C , т.е. ранг матрицы не изменяется приумножении ее слева или справа на невырожденную квадратную матрицу.

Теорема 3.6 о ранге суммы матриц. Ранг суммы матриц не превышает суммы рангов слагаемых:

operatorname{rg}(A+B)leqslant operatorname{rg}A+operatorname{rg}B.

Действительно, составим матрицу (A+Bmid Amid B) . Заметим, что каждый столбец матрицы A+B есть линейная комбинация столбцов матриц и . Поэтому operatorname{rg}(A+Bmid Amid B)= operatorname{rg}(Amid B) . Учитывая, что количество линейно независимых столбцов в матрице не превосходит operatorname{rg}A+operatorname{rg}B , а operatorname{rg}(A+B)leqslant operatorname{rg}(A+Bmid Amid B) (см. п.5 замечаний 3.2), получаем доказываемое неравенство.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Вторая часть.

Теорема 5:

Ранг матрицы и базисный минор матрицы

Теоремы о базисном миноре и о ранге матрицы

Условие равенства нулю определителя

Инвариантность ранга матрицы при элементарных преобразованиях

Ранге произведения и суммы матриц

Вам также может понравиться

Как найти тезис в русской литературе

Как найти объем новости

Как найти друга в lol

Добавить комментарий Отменить ответ