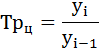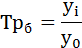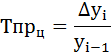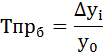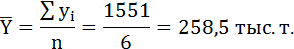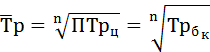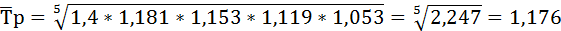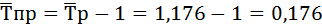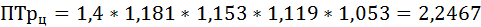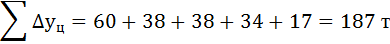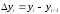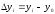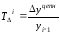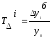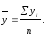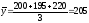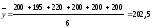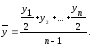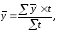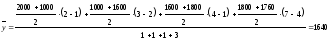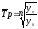Добыча нефти характеризуется следующими данными:
| Годы | Добыча нефти, тыс. т |
|---|---|
| 1-ый | 150 |
| 2-ой | 210 |
| 3-ий | 248 |
| 4-ый | 286 |
| 5-ый | 320 |
| 6-ой | 337 |
Произвести анализ ряда динамики по:
1) показателям, характеризующим рост добычи нефти (на цепной и базисной основе): абсолютный прирост, темпы роста и прироста (по годам к базисному году); результаты расчетов изложить в табличной форме;
2) средний уровень и среднегодовой темп ряда динамики;
3) показать взаимосвязь между цепными и базисными показателями.
Сделайте выводы.
Решение:
Абсолютный прирост цепной (Δyц) – это разность между текущим уровнем ряда и предыдущим:
Δyц =yi – yi-1
Так, во 2-ом г. прирост добычи нефти в сравнении с первым годом составит:
Δyц 2-й год = y2 – y1 =
= 210 – 150 = 60 тыс. т.
В 3-ем году прирост добычи нефти в сравнении со 2-м годом составит:
Δyц 3-й год = 248 – 210 = 38 тыс. т.
Аналогично исчисляются абсолютные приросты за последующие годы. Результаты расчётов занесём в таблицу.
Абсолютный прирост базисный (Δyб) – это разность между текущим уровнем ряда и уровнем ряда, выбранным за базу сравнения:
Δyб = yi – y0
Так как в задании не указано, какой год взять в качестве базисного года, по умолчанию будем считать базисным 1-й год.
Абсолютный прирост базисный во 2-ом г. совпадает с цепным абсолютным приростом в этом году:
Δyб = 210 – 150 = 60 тыс. т
в 3-ем году базисный абсолютный прирост равен:
Δyб = y3 – y2 = 248 – 150 = 98 тыс. т и т.д (гр. 3 расчётной таблицы).
Темп роста (Тр) – отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.
Цепной темп роста исчисляют отношением текущего уровня к предыдущему:
(гр. 5 расчётной таблицы);
базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения:
(гр. 4 расчётной таблицы).
Темп прироста (Тпр) так же может быть цепной или базисный.
Цепной рассчитывается как отношение абсолютного прироста к предыдущему уровню ряда динамики:
Базисный темп прироста рассчитывается как отношение абсолютного прироста к базисному уровню ряда динамики:
Если предварительно был вычислен темп роста, то темп прироста можно рассчитать как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах:
Тпр= Тр – 1;
или как разность между темпами роста и 100%, если темпы роста выражены в процентах:
Тпр= Тр – 100% (гр. 6 и 7 расчётной таблицы).
Расчётная таблица
| Годы | Добыча нефти, тыс. т | Абсолютный прирост базисный, тыс. т | Абсолютный прирост цепной, тыс. т | Темп роста базисный, % | Темп роста цепной, % | Темп прироста базисный, % | Темп прироста цепной, % |
|---|---|---|---|---|---|---|---|
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1-ый | 150 | 0 | – | 100,00 | – | – | – |
| 2-ой | 210 | 60 | 60 | 140,00 | 140,0 | 40,00 | 40,0 |
| 3-ий | 248 | 98 | 38 | 165,33 | 118,1 | 65,33 | 18,1 |
| 4-ый | 286 | 136 | 38 | 190,67 | 115,3 | 90,67 | 15,3 |
| 5-ый | 320 | 170 | 34 | 213,33 | 111,9 | 113,33 | 11,9 |
| 6-ой | 337 | 187 | 17 | 224,67 | 105,3 | 124,67 | 5,3 |
Из таблицы видно, что добыча нефти росла от года к году. Однако прирост добычи с каждым годом становился меньше.
2) Средний уровень ряда определяется в данном случае по формуле средней арифметической простой, где в числителе сумма уровней динамического ряда, а в знаменателе их число:
Среднегодовой темп роста ряда динамики рассчитывается по формуле средней геометрической
где ПТр – произведение цепных темпов роста (в коэффициентах),
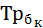
n – число темпов.
Среднегодовой темп прироста ряда динамики:
Добыча нефти ежегодно возрастала в среднем на 17,6%.
3) Между цепными и базисными темпами роста имеется взаимосвязь:
произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста.
Сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту:
Выводы: С 1 по 6 годы добыча нефти росла от года к году. Объём добычи нефти за эти годы вырос на 124,7%, что в абсолютном выражении составило 187 т. Однако ежегодный прирост добычи с каждым годом снижался. В среднем добыча нефти ежегодно возрастала на 17,6%.
Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —– | —– | 100.0 | 100.0 | —– | —– |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Показатели ряда динамики
Примеры решения задач
Задача 1
По АО
«Керамик» имеются данные о производстве кирпича за год. Рассчитайте все
недостающие в таблице уровни ряда и цепные показатели анализа динамики.
Рассчитайте средний уровень ряда, средние абсолютный прирост и темп роста.
| Месяцы |
Произведено кирпича, тыс.р. |
Цепные показатели | |||
| абсолютный | темп роста, % | темп прироста, % |
абсолютное значение 1% прироста |
||
| Январь | 450 | ||||
| Февраль | 100 | ||||
| Март | 80 | ||||
| Апрель | -30 | ||||
| Май | 250 | ||||
| Июнь | -30 | ||||
| Июль | |||||
| Август | 300 | 5,0 | |||
| Сентябрь | 150 | ||||
| Октябрь | 80 | ||||
| Ноябрь | -60 | ||||
| Декабрь | 300 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Формулы цепных показателей динамики
Абсолютный цепной прирост можно
найти по формуле:
-уровень ряда;
-предыдущий
уровень ряда
Цепной темп роста:
Темп прироста:
Абсолютное
содержание 1% прироста:
Расчет недостающих уровней ряда динамики
Исходя из формул, заполним
недостающие показатели:
Февраль:
Март:
Апрель:
Май:
Июнь:
Июль:
Август:
Сентябрь:
Октябрь:
Ноябрь:
Декабрь:
Вычисление цепных показателей динамики
|
Абсолютные приросты цепные: |
Темпы роста цепные: |
|
Темпы прироста цепные: |
Абсолютное содержание 1% прироста: |
Показатели динамики производства кирпича
| Месяцы |
Произведено кирпича, тыс.р. |
Цепные показатели |
|||
| абсолютный |
темп роста, % |
темп прироста, % |
абсолютное значение 1% прироста |
||
| Январь | 450 | —- | 100 | —- | —– |
| Февраль | 900 | 450 | 200 | 100 | 4.5 |
| Март | 720 | -180 | 80.0 | -20.0 | 9,0 |
| Апрель | 690 | -30 | 95.8 | -4.2 | 7.2 |
| Май | 1725 | 1035 | 250.0 | 150.0 | 6.9 |
| Июнь | 1208 | -517 | 70.0 | -30.0 | 17.25 |
| Июль | 500 | -708 | 41.4 | -58.6 | 12.08 |
| Август | 800 | 300 | 160.0 | 60.0 | 5,0 |
| Сентябрь | 1200 | 400 | 150.0 | 50.0 | 8,0 |
| Октябрь | 2160 | 960 | 180.0 | 80.0 | 12,0 |
| Ноябрь | 2100 | -60 | 97.2 | -2.8 | 21.6 |
| Декабрь | 6300 | 4200 | 300 | 200 | 21,0 |
Расчет средних уровней ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Вывод к задаче
Среднемесячный
показатель производства составил 1562,8 тыс.р. В среднем за месяц показатель
увеличивался на 531,8 тыс.р. или на 27,1% в относительном выражении.
Задача 2
Для
изучения динамики товаропотока рассчитайте:
- Абсолютные и относительные показатели динамики по годам периода (абсолютные
приросты – базисные и цепные; темпы роста – базисные и цепные). - Динамические средние за период в целом – среднегодовой уровень ряда,
среднегодовой абсолютный прирост, среднегодовой темп роста. Объясните их смысл. - Выполните прогнозы уровня ряда на следующий год, используя среднегодовой
абсолютный прирост и среднегодовой темп роста. Сделайте выводы о развитии
изучаемого процесса. - Постройте график динамики изучаемого процесса.
Динамика
экспорта РФ в Португалию, млрд. долл. США
| Годы | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Экспорт | 0.62 | 1.14 | 1.38 | 1.25 | 0.21 | 0.13 | 0.20 |
Решение
1)
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики экспорта 2004-2010 гг.
| Годы |
Экспорт, млрд.долл |
Абсолютные приросты, млрд.долл |
Темпы роста, % |
Темпы прироста, % |
|||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2004 | 0.62 | —– | —– | 100.0 | 100.0 | —– | —– |
| 2005 | 1.14 | 0.52 | 0.52 | 183.9 | 183.9 | 83.9 | 83.9 |
| 2006 | 1.38 | 0.24 | 0.76 | 121.1 | 222.6 | 21.1 | 122.6 |
| 2007 | 1.25 | -0.13 | 0.63 | 90.6 | 201.6 | -9.4 | 101.6 |
| 2008 | 0.21 | -1.04 | -0.41 | 16.8 | 33.9 | -83.2 | -66.1 |
| 2009 | 0.13 | -0.08 | -0.49 | 61.9 | 21.0 | -38.1 | -79.0 |
| 2010 | 0.20 | 0.07 | -0.42 | 153.8 | 32.3 | 53.8 | -67.7 |
2)
Средний уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Таким
образом в среднем за исследуемый период экспорт
составлял 0,704 млрд. долл. в год. В среднем показатель уменьшался на 0,07 млрд.долл. в год или на 17,2% в
относительном выражении.
3)
Прогноз на 2011 год с помощью среднего абсолютного прироста:
Прогноз
на 2011 год с помощью среднегодового темпа роста:
На
2011 год показатель, прогнозируемый с помощью среднего
абсолютного прироста составил 0,13 млрд. долл., а с помощью
среднегодового темпа роста – 0,166 млрд. долл.
4)
График динамики экспорта 2004-2010 гг.
Темпы
роста − это
отношение уровней ряда одного периода
к другому.
Темпы
роста могут быть вычислены как базисные,
когда все уровни ряда относятся к уровню
одного и того же периода, принятому за
базу:
Тр=
yi/y0
− базисный
темп роста
и
как цепные,- это отношение каждого уровня
ряда к уровню предыдущего периода:
Тр=
yi/yi-1
− цепной темп роста.
Темпы
роста могут быть выражены коэффициентом
или процентом.
Базисные
темпы роста характеризуют непрерывную
линию развития, а цепные − интенсивность
развития в каждом отдельном периоде,
причём произведение цепных темпов равно
темпу базисному. А частное от деления
базисных темпов равно промежуточному
цепному.
8.3 Прирост и темп прироста. Абсолютное значение 1% прироста.
Различают
понятие абсолютного и относительного
прироста. Абсолютный прирост вычисляют
как разность уровней ряда и выражают в
единицах измерения показателей ряда.
Если
из последующего уровня вычитается
предыдущий, то мы имеем цепной абсолютный
прирост:
Если
из каждого уровня вычитается один и тот
же уровень − базисный, то это базисный
абсолютный прирост:
Между
цепными и базисными абсолютными
приростами существует следующая
взаимосвязь: сумма последовательных
цепных приростов равна соответствующему
базисному приросту, характеризующему
общий прирост за весь соответствующий
период времени.
Относительную
оценку
значения абсолютного прироста по
сравнению с первоначальным уровнем
дают показатели темпа прироста (Т∆i).
Его определяют двумя способами:
-
Как
отношение абсолютного прироста (цепного)
к предыдущему уровню:
Это
цепной темп прироста.
Как
отношение базисного абсолютного прироста
к базисному уровню:
Это
базисный темп прироста.
2
Как разницу между темпом роста и единицей,
если темп роста выражен коэффициентом:
Т∆
= Тр-1,
или
Т∆
= Тр–
100, если темп роста выражен в процентах.
Темп
прироста
показывает, на сколько процентов
увеличились размеры явления за изучаемый
период. Если темп прироста имеет знак
минус, то говорят о темпах снижения.
Абсолютное
значение 1-го процента прироста
равно отношению абсолютного прироста
(цепного) к цепному темпу прироста,
выраженному в процентах:
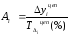
Этот
показатель можно также вычислить как
одну сотую часть предыдущего уровня:
Аi
= 0,01хУi;
8.4 Вычисление средних показателей динамики
Средний
уровень ряда
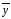
Средняя
хронологическая
− это средняя величина из показателей,
изменяющихся во времени.
В
интервальном ряду с равными интервалами
средний уровень ряда определяется по
формуле простой средней арифметической.
Средний
уровень ряда в интервальном ряду динамики
требует, чтобы было указано, за какой
период времени он вычислен (среднемесячный,
среднегодовой и т.д.).
Пример
1 Имеются
следующие данные о товарообороте,
ден.ед.:
|
Месяц |
январь |
февраль |
март |
|
Товарооборот |
200 |
195 |
220 |
Вычислить среднемесячный товарооборот
за первый квартал.
Т.к. нам дан интервальный ряд с равными
интервалами, применим формулу простой
средней арифметической:
Если
интервальный ряд имеет разные интервалы,
то его вначале нужно привести к ряду с
равными интервалами, а затем можно будет
использовать формулу простой средней
арифметической.
Пример
2 Имеются
следующие данные о товарообороте,
ден.ед.:
|
Месяц |
январь |
февраль |
март |
2-ой |
|
Товарооборот |
200 |
200 |
200 |
600 |
Будем считать, что во втором квартале
товарооборот распределялся по месяцам
равномерно, тогда среднемесячный
товарооборот за 1-ое полугодие:
Так
как показатели моментных рядов не
обладают свойством суммарности, то
среднюю нельзя вычислить, применяя
формулу простой средней арифметической,
в связи с тем, что остатки менялись
непрерывно в течение месяца, а данные
приводятся на определённый день.
Поэтому мы воспользуемся приближенным
методом, основанным на предположении,
что изучаемое явление менялось равномерно
в течение каждого месяца. Чем короче
будет интервал ряда, тем меньше ошибка
будет допущена при использовании этого
допущения.
Получим
формулу :
Эта
формула применяется для вычисления
среднего
уровня в моментных рядах с равными
интервалами.
Пример
3 Имеются
данные об остатках строительных
материалов на начало месяца, ден. ед.:
|
На |
1.01 |
1.02 |
1.03 |
1.04 |
|
Остатки |
2000 |
1000 |
1600 |
1800 |
Определить средний остаток за 1-й квартал.
Решение.
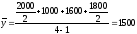
Если
интервалы в моментных рядах не равны,
то средний уровень ряда вычисляется по
формуле:
где
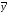
средний уровень в интервалах между
датами,
t
– период времени (интервал ряда)
Пример 4Имеются данные об остатках
сырья и материалов, ден. ед
|
На |
01.01 |
01.02 |
01.03 |
01.04 |
01.07 |
|
Остатки |
2000 |
1000 |
1600 |
1800 |
1760 |
Найти
среднемесячные остатки сырья и материалов
за первое полугодие.
Применяем
формулу:
Средний
абсолютный прирост вычисляется
двумя способами:
1
Как средняя арифметическая простая
годовых (цепных) приростов, т.е.
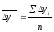
2 Как частное от деления базисного
прироста к числу периодов:
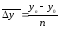
Расчет среднего абсолютного значения
1% приростаза несколько лет производится
по формуле простой средней арифметической:
При
вычислении среднегодового темпа роста
нельзя применять простую среднюю
арифметическую, т.к. сумма годовых темпов
не будет иметь смысла. В этом случае
применяют среднюю геометрическую, т.е.:
где
Трi
− годовые цепные темпы роста;
n
− число темпов.
Поскольку
произведение цепных темпов равно темпу
базисному, то средний темп роста может
быть рассчитан следующим образом:
Error: Reference source not found
При
расчёте по этой формуле не обязательно
знать годовые темпы роста. Величина
среднего темпа будет зависеть от
соотношения начального и конечного
уровня ряда.
Пример
5 Номинальная
заработная плата работников народного
хозяйства Республики Беларусь
характеризуется данными, представленными
в таблице 1.
Таблица
1 – Номинальная заработная плата
работников народного
хозяйства Республике Беларусь
|
Год |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
|
Размер |
558,9 |
1123,0 |
1189,2 |
2250,7 |
3347,5 |
4463,7 |
5582,2 |
7701,1 |
Для
анализа динамики заработной платы
определить:
-
среднегодовой
размер заработной платы за 8 лет; -
ежегодные
и базисные абсолютные приросты, темпы
роста и прироста заработной платы; -
абсолютное
значение 1% прироста; -
среднегодовой
абсолютный прирост; -
среднегодовой
темп роста и среднегодовой темп прироста; -
среднее
значение 1% прироста.
Результаты
представить в таблице, сделать выводы.
Решение
1
Среднегодовой размер заработной платы
определим по формуле средней арифметической
простой
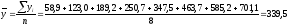
р.
2
Ежегодный (цепной) абсолютный прирост
(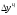
определим по формуле

где


в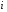
периоде и предшествующем ему.
Например,
для 2005 года
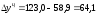
по сравнению с 2004 годом выросла на 64,1
тыс. р.; для 2006 года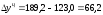
Базисный
абсолютный прирост (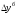
определим по формуле
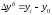
где
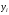
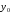
в
и базисном (2004 год) периоде.
Например,
для 2005 года
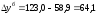
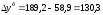
по сравнению с 2004 годом увеличилась на
130,3 тыс. р. и т. д.
Цепной
темп роста определим по формуле
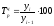
Например,
для 2005 года
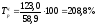
т. е. заработная плата в 2001 году по
сравнению с 2004 годом выросла на 108,8%; для
2006 года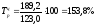
Базисный
темп роста определим по формуле
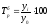
Например,
для 2001 года
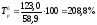
для 2002 года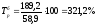
т. е. заработная плата в 2002 году по
сравнению с
2000 годом выросла на 221,2% и т. д.
Темп
прироста найдем по формуле
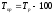
Так,
цепной темп прироста
за
2005 год: 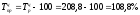
за
2006 год: 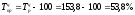
Базисный
темп прироста
за
2005 год: 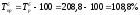
за
2006 год: 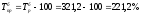
3
Абсолютное значение 1% прироста (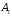
найдем по формуле

Этот
показатель можно также вычислить как
одну сотую часть предыдущего уровня:
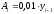
Например,
для 2005 года
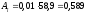
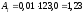
Расчеты
показателей по пунктам 1, 2, 3 оформим в
таблице 2
Таблица
2 – Показатели динамики заработной
платы за 2004-2011 гг.
|
Год |
Размер заработной тыс.р. |
Абсолютный |
Темп |
Темп |
Абсолютное |
|||
|
Цепной |
базисный |
цепной |
базисный |
цепной |
базисный |
|||
|
2004 |
58,9 |
– |
– |
– |
100 |
– |
– |
– |
|
2005 |
123,0 |
64,1 |
64,1 |
208,8 |
208,8 |
108,8 |
108,8 |
0,589 |
|
2006 |
189,2 |
66,2 |
130,3 |
153,8 |
321,2 |
53,8 |
221,2 |
1,23 |
|
2007 |
250,7 |
61,5 |
191,8 |
132,5 |
425,6 |
32,5 |
325,6 |
1,892 |
|
2008 |
347,5 |
96,8 |
288,6 |
138,6 |
590 |
38,6 |
490 |
2,507 |
|
2009 |
463,7 |
116,2 |
404,8 |
133,4 |
787,3 |
33,4 |
687,3 |
3,475 |
|
2010 |
582,2 |
118,5 |
523,3 |
125,6 |
988,5 |
25,6 |
888,5 |
4,637 |
|
2011 |
701,1 |
118,9 |
642,2 |
120,4 |
1190,3 |
20,4 |
1090,3 |
5,822 |
4
Среднегодовой абсолютный прирост
вычисляется двумя способами:
– как
средняя арифметическая простая годовых
(цепных) приростов, т.е.:
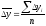
– как
частное от деления базисного прироста
к числу периодов
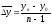
Так
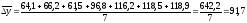
р.
или
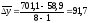
5
Среднегодовой темп роста найдем по
формуле
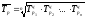
где

или

где

Так
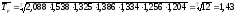
Либо
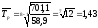
Среднегодовой
темп роста заработной платы за 2004-2011
гг. составляет 143%, следовательно,
среднегодовой прирост составит 43%.
6
Среднее значение 1% прироста рассчитаем
по формуле
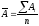
Так
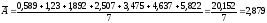
Таким
образом, на протяжении 2004-2011 гг. наблюдается
положительная динамика роста заработной
платы. Так, среднегодовой абсолютный
прирост составил 91,7 тыс. р. или 43%.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Анна
Ученик
(197),
на голосовании
13 лет назад
Голосование за лучший ответ
Вика
Гуру
(3836)
13 лет назад
= отчетный период (2ой год) *100/на базовый период (1год)
Ксюша Л
Гуру
(4118)
13 лет назад
Отчетный/базисный*100%
Похожие вопросы