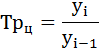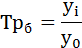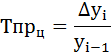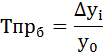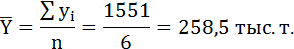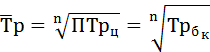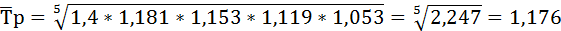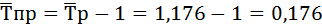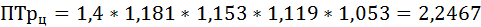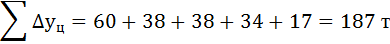Цепные:
Базисные:
2. Определяем цепные и базисные темпы
роста (Т).
Цепные:
Базисные:
3. Определяем цепные и базисные
абсолютные приросты ().
Цепные:
Базисные:
4. Определяем цепные и базисные темпы
прироста ().
Цепные:
Базисные:
Проверим связь между базисными и цепными
абсолютными приростами:
.
Проверим связь между базисными и цепными
коэффициентами роста:
.
1.8.5. Определение
средних показателей динамики
По показателям
изменения уровней ряда динамики
(абсолютные приросты, темпы роста и
прироста), полученным в результате
анализа исходного ряда, могут быть
рассчитаны обобщающие показатели в
виде средних величин – средний абсолютный
прирост, средний темп роста, средний
темп прироста.
Средний абсолютный
прирост
может быть получен по одной из формул:
или
,
гдеn
– число уровней ряда динамики;
– первый уровень
ряда динамики;
–
последний уровень ряда динамики;
– цепные абсолютные
приросты.
Средний коэффициент
роста можно
определить, пользуясь формулами:
;
;
,
где n
– число рассчитанных цепных или базисных
темпов роста;
– уровень ряда,
принятый за базу для сравнения;
– последний уровень
ряда;
– цепные коэффициенты
роста;
– первый базисный
коэффициент роста;
–
последний базисный коэффициент роста.
Средний темп
роста
вычисляется по формуле:
.
Средний темп
прироста:
,
или
.
Средняя величина
абсолютного значения 1% прироста:
1.8.6. Определение в рядах динамики общей тенденции развития (тренд)
Определение уровней
ряда динамики на протяжении длительного
периода времени обусловлено действием
ряда факторов, которые неоднородны по
силе и направлению воздействия,
оказываемого на изучаемое явление.
Рассматривая
динамические ряды, пытаются разделить
эти факторы на постоянно действующие
и оказывающие определяющее воздействие
на уровни ряда, формирующие основную
тенденцию развития, и случайные факторы,
приводящие к кратковременным изменениям
уровней ряда динамики. Наиболее важна
при анализе ряда динамики его основная
тенденция развития (тренд), но часто по
одному лишь внешнему виду ряда динамики
ее установить невозможно, поэтому
используют специальные методы обработки,
позволяющие показать основную тенденцию
ряда. Методы обработки используются
как простые, так и достаточно сложные.
Простейший способ
обработки ряда динамики, применяемый
с целью установления закономерностей
развития – метод
укрупнения интервалов.
Суть метода в том,
чтобы от интервалов, или периодов
времени, для которых определены исходные
уровни ряда динамики, перейти к более
продолжительным периодам времени и
посмотреть, как уровни ряда изменяются
в этом случае.
Пример.
Данные о реализации молочной продукции
в магазинах города по месяцам представлены
таблицей (в тоннах)
|
месяц |
1987 |
1988 |
1989 |
|
январь |
5,3 |
5,3 |
5,4 |
|
февраль |
5,3 |
5,1 |
5,2 |
|
март |
7,9 |
8,3 |
8,2 |
|
апрель |
8,2 |
9,0 |
9,3 |
|
май |
9,8 |
9,5 |
10,1 |
|
июнь |
12,5 |
13,0 |
13,1 |
|
июль |
11,8 |
12,2 |
12,5 |
|
август |
10,3 |
10,4 |
10,8 |
|
сентябрь |
8,2 |
8,0 |
8,3 |
|
октябрь |
6,5 |
6,6 |
6,8 |
|
ноябрь |
5,4 |
5,5 |
5,7 |
|
декабрь |
5,5 |
5,5 |
5,6 |
|
итого за |
96,7 |
98,4 |
101 |
Исходные уровни
ряда динамики подвержены сезонным
изменениям; для определения общей
тенденции развития переходят от
ежемесячных уровней к годовым уровням:
1987г. – 96,7 тонн
1988г. – 98,4 тонн
1989г. – 101 тонна
Эти цифры, полученные
в результате перехода к годовым уровням
ряда динамики, показывают общую тенденцию
роста реализации молочной продукции.
Другой способ
определения тенденции в ряду динамики
— метод
скользящих средних.
Суть метода заключается в том, что
фактические уровни ряда заменяются
средними уровнями, вычисленными по
определённому правилу, например:
—исходные или
фактические уровни ряда динамики
заменяются средними уровнями:
…
…
…
В результате
получается сглаженный ряд, состоящий
из скользящих пятизвенных средних
уровней
.
Между расположением уровнейи
устанавливается соответствие:
— —
— —,
сглаженный ряд
короче исходного на число уровней
,
где k – число уровней, выбранных для
определения средних уровней ряда.
Сглаживание методом
скользящих средних можно производить
по четырём, пяти или другому числу
уровней ряда, используя соответствующие
формулы для усреднения исходных уровней.
Полученные при
этом средние уровни называются
четырёхзвенными скользящими средними,
пятизвенными скользящими средними и
т.д.
При сглаживании
ряда динамики по чётному числу уровней
выполняется дополнительная операция,
называемая центрированием, поскольку,
при вычислении скользящего среднего,
например по четырём уровням,
относится к временной точке между
моментами времени, когда были зафиксированы
фактические уровнии
.
Схема вычислений и расположений уровней
сглаженного ряда становится сложнее:
… — исходные
уровни;
— —
…
— сглаженные уровни;
— —
…
— центрированные сглаженные уровни;
.
Метод скользящих
средних не позволяет получить численные
оценки для выражения основной тенденции
в ряду динамики, давая лишь наглядное
графическое представление (пример 1).
Пример.
Таблица 1.
|
Годы |
Валовый |
Скользящая |
|
1960 |
4,3 |
— |
|
1961 |
4,5 |
— |
|
1962 |
4,3 |
4,72 |
|
1963 |
5,2 |
5,00 |
|
1964 |
5,3 |
5,30 |
|
1965 |
5,7 |
5,64 |
|
1966 |
6,0 |
5,78 |
|
1967 |
6,0 |
5,86 |
|
1968 |
5,9 |
6,10 |
|
1969 |
5,7 |
6,32 |
|
1970 |
6,9 |
6,58 |
|
1971 |
7,1 |
6,94 |
|
1972 |
7,3 |
7,48 |
|
1973 |
7,7 |
7,68 |
|
1974 |
8,4 |
7,92 |
|
1975 |
7,9 |
8,22 |
|
1976 |
8,3 |
8,38 |
|
1977 |
8,8 |
8,54 |
|
1978 |
8,5 |
8,94 |
|
1979 |
9,2 |
9,18 |
|
1980 |
9,9 |
9,30 |
|
1981 |
9,6 |
— |
|
1982 |
9,3 |
— |
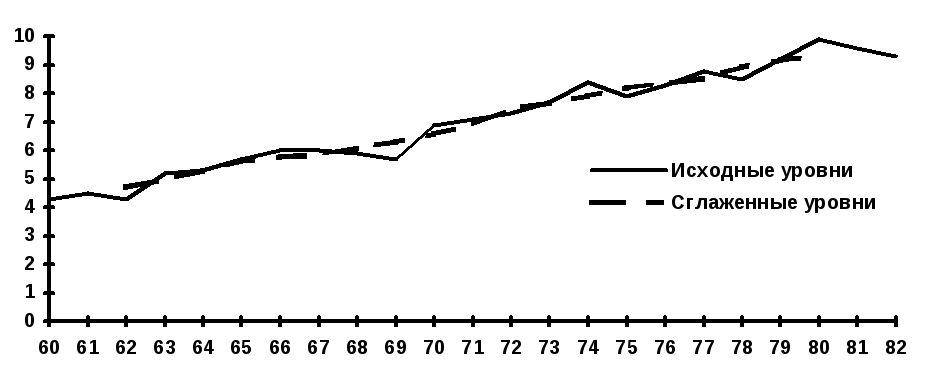
На рис. 1 показан
график, построенный по данным о валовом
сборе хлопка-сырца в стране за ряд лет
наблюдения и по расчетным данным,
представленным в таблице 1.
Рис. 1. Валовый
сбор хлопка – сырца
Наиболее совершенным
способом определения тенденции развития
в ряду динамики является метод
аналитического выравнивания. При этом
методе исходные уровни ряда динамики
заменяются теоретическими или расчетными
,
которые представляют из себя некоторую
достаточно простую математическую
функцию времени, выражающую общую
тенденцию развития ряда динамики. Чаще
всего в качестве такой функции выбирают
прямую, параболу, экспоненту и др.
Например,
,
где
– коэффициенты, определяемые в методе
аналитического выравнивания;
– моменты времени,
для которых были получены исходные и
соответствующие теоретические уровни
ряда динамики, образующие прямую,
определяемую коэффициентами
.
Расчет коэффициентов
ведется на основе метода наименьших
квадратов:
Если вместо
подставить
(или соответствующее выражение для
других математических функций), получим:
Это функция двух
переменных
(все
и
известны), которая при определенных
достигает минимума. Из этого выражения
на основе знаний, полученных в курсе
высшей математики об экстремуме функций
n переменных, получают значения
коэффициентов.
Для прямой:
где n — число
моментов времени, для которых были
получены исходные уровни ряда
.
Если вместо
абсолютного времени
выбрать
условное время таким образом, чтобы,
то записанные выражения для определенияупрощаются:
Пример.
Нечетное число уровня ряда.
|
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
абсолютное |
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
условное |
Чётное число уровней ряда.
|
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
абсолютное |
|
-7 |
-5 |
-3 |
-1 |
1 |
3 |
5 |
7 |
условное |
В обоих случаях
.
Пример.
Выполняется аналитическое выравнивание
ряда, отражающего производство стали
в стране по годам (млн. т).
|
1985 |
1986 |
1987 |
1988 |
1989 |
|
141,3 |
144,8 |
146,7 |
151,5 |
149,0 |
В качестве математической функции,
отражающей тенденцию развития, выбирается
прямая
,
определениепроизводится для условного времени, в
результате,
.
|
Год |
Производство |
Условное время |
Теоретические уровни |
|
1985 |
141,3 |
-2 |
142,2 |
|
1986 |
144,8 |
-1 |
144,4 |
|
1987 |
146,7 |
0 |
146,7 |
|
1988 |
151,5 |
1 |
148,9 |
|
1989 |
149,0 |
2 |
151,1 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —– | —– | 100.0 | 100.0 | —– | —– |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Добыча нефти характеризуется следующими данными:
| Годы | Добыча нефти, тыс. т |
|---|---|
| 1-ый | 150 |
| 2-ой | 210 |
| 3-ий | 248 |
| 4-ый | 286 |
| 5-ый | 320 |
| 6-ой | 337 |
Произвести анализ ряда динамики по:
1) показателям, характеризующим рост добычи нефти (на цепной и базисной основе): абсолютный прирост, темпы роста и прироста (по годам к базисному году); результаты расчетов изложить в табличной форме;
2) средний уровень и среднегодовой темп ряда динамики;
3) показать взаимосвязь между цепными и базисными показателями.
Сделайте выводы.
Решение:
Абсолютный прирост цепной (Δyц) – это разность между текущим уровнем ряда и предыдущим:
Δyц =yi – yi-1
Так, во 2-ом г. прирост добычи нефти в сравнении с первым годом составит:
Δyц 2-й год = y2 – y1 =
= 210 – 150 = 60 тыс. т.
В 3-ем году прирост добычи нефти в сравнении со 2-м годом составит:
Δyц 3-й год = 248 – 210 = 38 тыс. т.
Аналогично исчисляются абсолютные приросты за последующие годы. Результаты расчётов занесём в таблицу.
Абсолютный прирост базисный (Δyб) – это разность между текущим уровнем ряда и уровнем ряда, выбранным за базу сравнения:
Δyб = yi – y0
Так как в задании не указано, какой год взять в качестве базисного года, по умолчанию будем считать базисным 1-й год.
Абсолютный прирост базисный во 2-ом г. совпадает с цепным абсолютным приростом в этом году:
Δyб = 210 – 150 = 60 тыс. т
в 3-ем году базисный абсолютный прирост равен:
Δyб = y3 – y2 = 248 – 150 = 98 тыс. т и т.д (гр. 3 расчётной таблицы).
Темп роста (Тр) – отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.
Цепной темп роста исчисляют отношением текущего уровня к предыдущему:
(гр. 5 расчётной таблицы);
базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения:
(гр. 4 расчётной таблицы).
Темп прироста (Тпр) так же может быть цепной или базисный.
Цепной рассчитывается как отношение абсолютного прироста к предыдущему уровню ряда динамики:
Базисный темп прироста рассчитывается как отношение абсолютного прироста к базисному уровню ряда динамики:
Если предварительно был вычислен темп роста, то темп прироста можно рассчитать как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах:
Тпр= Тр – 1;
или как разность между темпами роста и 100%, если темпы роста выражены в процентах:
Тпр= Тр – 100% (гр. 6 и 7 расчётной таблицы).
Расчётная таблица
| Годы | Добыча нефти, тыс. т | Абсолютный прирост базисный, тыс. т | Абсолютный прирост цепной, тыс. т | Темп роста базисный, % | Темп роста цепной, % | Темп прироста базисный, % | Темп прироста цепной, % |
|---|---|---|---|---|---|---|---|
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1-ый | 150 | 0 | – | 100,00 | – | – | – |
| 2-ой | 210 | 60 | 60 | 140,00 | 140,0 | 40,00 | 40,0 |
| 3-ий | 248 | 98 | 38 | 165,33 | 118,1 | 65,33 | 18,1 |
| 4-ый | 286 | 136 | 38 | 190,67 | 115,3 | 90,67 | 15,3 |
| 5-ый | 320 | 170 | 34 | 213,33 | 111,9 | 113,33 | 11,9 |
| 6-ой | 337 | 187 | 17 | 224,67 | 105,3 | 124,67 | 5,3 |
Из таблицы видно, что добыча нефти росла от года к году. Однако прирост добычи с каждым годом становился меньше.
2) Средний уровень ряда определяется в данном случае по формуле средней арифметической простой, где в числителе сумма уровней динамического ряда, а в знаменателе их число:
Среднегодовой темп роста ряда динамики рассчитывается по формуле средней геометрической
где ПТр – произведение цепных темпов роста (в коэффициентах),
n – число темпов.
Среднегодовой темп прироста ряда динамики:
Добыча нефти ежегодно возрастала в среднем на 17,6%.
3) Между цепными и базисными темпами роста имеется взаимосвязь:
произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста.
Сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту:
Выводы: С 1 по 6 годы добыча нефти росла от года к году. Объём добычи нефти за эти годы вырос на 124,7%, что в абсолютном выражении составило 187 т. Однако ежегодный прирост добычи с каждым годом снижался. В среднем добыча нефти ежегодно возрастала на 17,6%.

Гражданское право – работа с недвижимостью. договорная работа, наследственное право, банкротство.
Важнейшим показателем эффективности производства в анализе финансовой ситуации компании является показатель темпа роста. Поговорим об особенностях его расчета.
Как рассчитать темп роста: формула
Что называют снижением темпа роста цен?
Подробнее
Этот термин показывает изменение значения любого экономического или статистического показателя в текущем периоде к его начальному значению (являющемуся базовым) за определенный временной промежуток. Измеряется он в процентах или коэффициентах.
Например, при сравнении объема выпуска товаров на конец года (допустим, в значении 100000 руб.) к показателю объема на начало года (70000 руб.) темп роста находят отношением конечного значения к начальному: 100000 / 70000 = 1,428. Индекс роста в примере составил 1,429. Это означает, что на конец года объем выпуска составил 142,9%.
Как рассчитать темп роста в процентах – формула:
ТР = Пт / Пб х 100%,
где Пк и Пб – показатели значений текущего и базового периодов.
Узнайте, может ли темп роста быть отрицательной величиной.
Темп роста показывает интенсивность изменений какого-либо процесса по отношению к его начальному (базовому) значению. Результат вычислений – один из трех вариантов:
-
ТР больше 100%, следовательно, конечное значение возросло в сравнении с начальным, т.е. налицо рост показателя;
-
ТР = 100%, т.е. изменений ни в большую, ни в меньшую сторону не произошло – показатель остался на прежнем уровне;
-
ТР меньше 100%, значит, анализируемый показатель снизился к началу периода.
Приведем примеры, как рассчитать темп роста в процентах по каждому варианту расчета, объединив исходные данные в таблицу:
|
Объем выпуска в тыс. руб. |
Расчет (Пт / Пб х 100%) |
|
|
2017 (Пб) |
2018 (Пт) |
|
|
600 |
800 |
133,3% |
|
600 |
600 |
100% |
|
600 |
400 |
66,7% |
Такой темп роста называют базисным, поскольку база сравнения по периодам остается неизменной – показатель на начало периода. Если же сравнительная база изменяется, а темп роста вычисляют отношением текущего значения к предыдущему (а не базисному), то этот показатель будет цепным.
Узнайте, чем отличается темп роста от темпа прироста.
Как рассчитать цепные темпы роста
Рассмотрим пример расчета базисного и цепного темпов роста:
|
Период |
Объем в тыс.руб. |
Темп роста в % |
|
|
базисный |
цепной |
||
|
1 кв. |
300 |
100 |
– |
|
2 кв. |
310 |
103,3 (310 / 300) |
103,3 (310 / 300) |
|
3 кв. |
280 |
93,3 (280 / 300) |
90,3 (280 / 310) |
|
4 кв. |
360 |
120 (360 / 300) |
128,6 (360 / 280) |
Цепные темпы роста характеризуют насыщенность изменения уровней от квартала к кварталу, базисные же отражают ее в целом за весь временной интервал (показатель 1 квартала – база сравнения).
Сравнивая показатели в приведенном примере, можно отметить, что ряд значений, рассчитанных к началу периода, имеет меньшую амплитуду колебаний, чем цепные показатели, вычисления которых привязаны не к началу года, а к каждому предшествующему кварталу.
Как рассчитать темпы прироста
Кроме расчета темпов роста, принято высчитывать и темпы прироста. Эти значения также бывают базисными и цепными. Базисный прирост определяют как отношение разности показателей текущего и базового периодов к значению базового периода по формуле:
∆ ТР = (Птек – Пбаз) / Пбаз х 100%
Цепной прирост рассчитывают как разность между текущим и предыдущим показателями, деленную на темп роста предыдущего периода:
∆ ТР = (Птек – Ппр.п) / Ппр. п х 100%.
Более простым способом расчета является формула: ∆ ТР = ТР – 100%, где расчетные показатели темпа роста уменьшаются на 100%, т. е. исходную величину. Показатель темпа прироста в отличие от значений темпа роста может иметь отрицательное значение, поскольку темп роста (или снижения) показывает динамику изменений показателя, а темп прироста говорит о том, какой характер они носят.
Продолжая пример, рассчитаем приросты объемов в рассматриваемых периодах:
|
Период |
Темпы прироста |
|
|
базисные |
цепные |
|
|
1 кв. |
– |
– |
|
2 кв. |
3,3% (103,3 – 100) или ((310 – 300) / 300 х 100) |
3,3% (103,3 – 100) или ((310 – 300) / 300 х 100) |
|
3 кв. |
– 6,7% (93,3 – 100) или ((280 – 300) / 300 х 100) |
-9,7% (90,3 – 100) или ((280 – 310) / 310 х 100) |
|
4 кв. |
20% (120 – 100) или (( 360 – 300) / 300 х 100) |
28,6% (128,6 – 100) или ((360 – 280) / 280 х 100) |
Анализируя результаты вычислений, экономист может сделать вывод:
-
Прирост объемов наблюдался во 2-м и 4-м кварталах, причем во 2-м он был наименьшим (3,3%). В 3-м квартале объем выпуска сократился на 6,7% в сравнении с показателями начала года;
-
Цепные темпы прироста обнаружили более глубокие колебания: объемы 3-го квартала снизились по отношению к показателям 2-го на 9,7%. Зато выпуск товаров в 4-м квартале вырос почти на треть в сравнении с итогами 3-го квартала. Столь существенные изменения в объемах производства могут свидетельствовать о сезонности выпускаемых продуктов, перебоях в снабжении необходимым сырьем или других причинах, которые исследует аналитик.
Как рассчитать средний темп роста
Средний темп роста – обобщающая характеристика уровня изменений. Расчет средних темпов роста и прироста также разграничивают на базисные и цепные. Для определения среднего темпа роста расчетные показатели по периодам складывают и делят на количество периодов. Таким же образом находят и средние темпы приростов. Вернемся к предыдущему примеру, рассчитав средние значения базисных темпов роста и прироста, а также аналогичных цепных показателей.
|
Показатель |
Значение в % |
Расчет |
|
Средний темп роста (базисный) |
105,5 |
(103,3 + 93,3 + 120) / 3 |
|
Средний темп прироста (базисный) |
5,5 |
(3,3 – 6,7 + 20) / 3 |
|
Средний темп роста (цепной) |
107,4 |
(103,3 + 90,3 + 128,6) / 3 |
|
Средний темп прироста (цепной) |
7,4 |
(3,3 – 9,7 + 28,6) / 3 |
Полученные цифры свидетельствуют о том, что в среднем с начала года объемы выпуска выросли на 5,5%, а в поквартальной привязке рост составил 7,4%.
Читайте также: Экспресс-анализ финансового состояния предприятия

Специализация: Гражданское право – работа с недвижимостью. договорная работа, наследственное право, банкротство.
Окончила в 2005 г. Тверской государственный университет, юридический факультет, специальность-юриспруденция.
Юрист в сфере недвижимости:составление договоров, регистрация в Росреестре прав и сделок,оформление наследственных прав,
сопровождение сделок с недвижимым имуществом,судебный опыт по делам,связанным с признанием прав на недвижимость.
Имеется опыт работы помощником арбитражного управляющего.
Темп роста – это один из основных показателей динамических рядов, который характеризует процентное изменение во времени каких-либо значений (статистических величин).
Этот показатель связан с коэффициентом роста.
Коэффициент роста равен отношению текущего значения величины к предшествующему:
Кр = Y1 / Y0.
А темп роста представляет собой коэффициент роста, выраженный в процентах:
Тр = Y1 / Y0 * 100%
или по-другому:
Тр = Кр * 100%.
Если Кр > 1 и Тр > 100% – имеется рост изучаемого явления.
Если Кр = 0 и Тр = 100% – стабильность, не было изменений.
Если Кр < 1 и Тр < 100% – спад изучаемого явления.
Например, доход предприятия в первый год его существования составил 100 000 руб., а на второй год доход стал равен 120 000 руб.
Для нахождения темпа роста дохода нужно разделить 120000 на 100000 и умножить полученное значение на 100%.
В итоге темп роста будет равен 120%, то есть динамика положительная.
Существует два вида расчёта – цепной и базисный.
Цепной темп роста показывает процентное изменение текущего уровня ряда по сравнению со значением в предыдущем периоде.
Формула будет такая:
Базисный темп роста показывает процентное изменение текущего уровня ряда по сравнению с базисным.
Формула:
За базис обычно применяется самый первый уровень ряда, и с ним сравниваются все остальные показатели.
Но также в качестве базиса может использоваться и другое значение, выбранное по определённому признаку (например, может быть выбран показатель в том году, когда совершили модернизацию оборудования для увеличения производительности труда).
По такому же принципу считаются и базисные / цепные темпы прироста – в первом случае в формуле всегда используется первоначальное (исходное) значение, во втором – значение в предыдущем периоде.
Пример.
В таблице дан объём производства за 2016 – 2020 гг.
Нужно определить базисные и цепные темпы роста за каждый год.
За базис возьмём объём продукции, выпущенной в 2016 году – в нём базисный темп роста можно считать как 100%.
За остальные годы считаем по приведённым выше формулам.
Базисный:
1) 2017 год: Тр = (600 / 590) * 100% = 101,69%.
2) 2018 год: Тр = (610 / 590) * 100% = 103,39%.
3) 2019 год: Тр = (605 / 590) * 100% = 102,54%.
4) 2020 год: Тр = (615 / 590) * 100% = 104,24%.
Можно сделать вывод, что за эти годы производство продукции увеличилось на 4,24%, но рост был неравномерный из-за спада в 2019 году.
Цепной:
1) 2017 год: Тр = (600 / 590) * 100% = 101,69%.
2) 2018 год: Тр = (610 / 600) * 100% = 101,67%.
3) 2019 год: Тр = (605 / 610) * 100% = 99,18%.
4) 2020 год: Тр = (615 / 605) * 100% = 101,65%.
В 2019 году был спад производства на 0,82% по сравнению с предыдущим годом, в остальные периоды – увеличение.