Как найти бесконечно малую величину

Как найти бесконечно малую величину

Бесконечно малая — числовая функция или последовательность, предел которой равен нулю.

Бесконечно большая — числовая функция или последовательность, стремящаяся к (предел которой равен) бесконечности определённого знака.

В нестандартном анализе бесконечно малые и бесконечно большие определяются не как последовательности и не как переменные величины, а как особый вид чисел.

Исчисление бесконечно малых и больших[править | править код]

Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.

Бесконечно малая[править | править код]

Последовательность a_n называется бесконечно малой, если lim limits _{{nto infty }}a_{n}=0. Например, последовательность чисел a_{n}={dfrac {1}{n}} — бесконечно малая.

Функция называется бесконечно малой в окрестности точки x_{0}, если lim limits _{{xto x_{0}}}f(x)=0.

Функция называется бесконечно малой на бесконечности, если lim limits _{{xto +infty }}f(x)=0 либо lim limits _{{xto -infty }}f(x)=0.

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если lim limits _{{xto +infty }}f(x)=a, то f(x)-a=alpha (x), lim limits _{{xto +infty }}(f(x)-a)=0.

Подчеркнём, что бесконечно малую величину следует понимать как переменную величину (функцию), которая лишь в процессе своего изменения [при стремлении x к a (из lim limits _{{xto a}}f(x)=0)] делается меньше произвольного числа (varepsilon ). Поэтому, например, утверждение типа «одна миллионная есть бесконечно малая величина» неверно: о числе [абсолютном значении] не имеет смысла говорить, что оно бесконечно малое.[1]

Бесконечно большая[править | править код]

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsin x, неограниченная с обеих сторон, не является бесконечно большой при xto +infty .

Последовательность a_n называется бесконечно большой, если lim limits _{{nto infty }}a_{n}=infty .

Функция называется бесконечно большой в окрестности точки x_{0}, если lim limits _{{xto x_{0}}}f(x)=infty .

Функция называется бесконечно большой на бесконечности, если lim limits _{{xto +infty }}f(x)=infty либо lim limits _{{xto -infty }}f(x)=infty .

Как и в случае бесконечно малых, необходимо отметить, что ни одно отдельно взятое значение бесконечно большой величины не может быть названо как «бесконечно большое» — бесконечно большая величина — это функция, которая лишь в процессе своего изменения может стать больше произвольно взятого числа.

Свойства бесконечно малых[править | править код]

Сравнение бесконечно малых[править | править код]

Определения[править | править код]

Допустим, у нас есть бесконечно малые при одном и том же xto a величины alpha(x) и beta(x) (либо, что не важно для определения, бесконечно малые последовательности).

Для вычисления подобных пределов удобно использовать правило Лопиталя.

Примеры сравнения[править | править код]

С использованием О-символики полученные результаты могут быть записаны в следующем виде x^{5}=o(x^{3}).
В данном случае справедливы записи 2x^{2}+6x=O(x) и x=O(2x^{2}+6x).

Эквивалентные величины[править | править код]

Определение[править | править код]

Если lim limits _{{xto a}}{dfrac {beta }{alpha }}=1, то бесконечно малые или бесконечно большие величины alpha и beta называются эквивалентными (обозначается как alpha thicksim beta ).

Очевидно, что эквивалентные величины являются частным случаем бесконечно малых (бесконечно больших) величин одного порядка малости.

При alpha (x){xrightarrow[ {xto x_{0}}]{}}0 справедливы следующие соотношения эквивалентности (как следствия из так называемых замечательных пределов):

{sqrt[ {n}]{1+alpha (x)}}approx {frac {alpha (x)}{n}}+1, где alpha (x){xrightarrow[ {xto x_{0}}]{}}0.

Теорема[править | править код]

Предел частного (отношения) двух бесконечно малых или бесконечно больших величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.

Данная теорема имеет прикладное значение при нахождении пределов (см. пример).

Примеры использования[править | править код]

  • Найти lim limits _{{xto 0}}{dfrac {sin 2x}{x}}.
Заменяя sin 2x эквивалентной величиной 2x, получаем
lim limits _{{xto 0}}{dfrac {sin 2x}{x}}=lim limits _{{xto 0}}{dfrac {2x}{x}}=2.
  • Найти lim limits _{{xto {frac {pi }{2}}}}{dfrac {sin(4cos x)}{cos x}}.
Так как sin(4cos x)thicksim {4cos x} при xto {dfrac {pi }{2}} получим
lim limits _{{xto {frac {pi }{2}}}}{dfrac {sin(4cos x)}{cos x}}=lim limits _{{xto {frac {pi }{2}}}}{dfrac {4cos x}{cos x}}=4.
  • Вычислить {sqrt {1{,}2}}.
Используя формулу: {sqrt {1{,}2}}approx 1+{frac {0{,}2}{2}}=1{,}1, тогда как, используя калькулятор (более точные вычисления), получили: {sqrt {1{,}2}}approx 1{,}095, таким образом ошибка составила 0,005 (менее 1 %), то есть метод полезен, благодаря своей простоте, при грубой оценке арифметических корней близких к единице.

История[править | править код]

Понятие «бесконечно малое» обсуждалось ещё в античные времена в связи с концепцией неделимых атомов, однако в классическую математику не вошло. Вновь оно возродилось с появлением в XVI веке «метода неделимых» — разбиения исследуемой фигуры на бесконечно малые сечения.

В XVII веке произошла алгебраизация исчисления бесконечно малых. Они стали определяться как числовые величины, которые меньше всякой конечной (положительной) величины и всё же не равны нулю. Искусство анализа заключалось в составлении соотношения, содержащего бесконечно малые (дифференциалы), и затем — в его интегрировании.

Математики старой школы подвергли концепцию бесконечно малых резкой критике. Мишель Ролль писал, что новое исчисление есть «набор гениальных ошибок»; Вольтер ядовито заметил, что это исчисление представляет собой искусство вычислять и точно измерять вещи, существование которых не может быть доказано. Даже Гюйгенс признавался, что не понимает смысла дифференциалов высших порядков.

Споры в Парижской Академии наук по вопросам обоснования анализа приобрели настолько скандальный характер, что Академия однажды вообще запретила своим членам высказываться на эту тему (в основном это касалось Ролля и Вариньона). В 1706 году Ролль публично снял свои возражения, однако дискуссии продолжались.

В 1734 году известный английский философ, епископ Джордж Беркли выпустил нашумевший памфлет, известный под сокращённым названием «Аналитик». Полное его название: «Аналитик или рассуждение, обращённое к неверующему математику, где исследуется, более ли ясно воспринимаются или более ли очевидно выводятся предмет, принципы и умозаключения современного анализа, чем религиозные таинства и догматы веры». «Аналитик» содержал остроумную и во многом справедливую критику исчисления бесконечно малых. Метод анализа Беркли считал несогласным с логикой и писал, что, «как бы он ни был полезен, его можно рассматривать только как некую догадку; ловкую сноровку, искусство или скорее ухищрение, но не как метод научного доказательства». Цитируя фразу Ньютона о приращении текущих величин «в самом начале их зарождения или исчезновения», Беркли иронизирует: «это ни конечные величины, ни бесконечно малые, ни даже ничто. Не могли ли бы мы их назвать призраками почивших величин?.. И как вообще можно говорить об отношении между вещами, не имеющими величины?.. Тот, кто может переварить вторую или третью флюксию [производную], вторую или третью разность, не должен, как мне кажется, придираться к чему-либо в богословии».

Невозможно, пишет Беркли, представить себе мгновенную скорость, то есть скорость в данное мгновение и в данной точке, ибо понятие движения включает понятия о (конечных ненулевых) пространстве и времени.

Как же с помощью анализа получаются правильные результаты? Беркли пришёл к мысли, что это объясняется наличием в аналитических выводах взаимокомпенсации нескольких ошибок, и проиллюстрировал это на примере параболы. Как ни странно, некоторые крупные математики (например, Лагранж) согласились с ним.

Сложилась парадоксальная ситуация, когда строгость и плодотворность в математике мешали одна другой. Несмотря на использование незаконных действий с плохо определёнными понятиями, число прямых ошибок было на удивление малым — выручала интуиция. И всё же весь XVIII век математический анализ бурно развивался, не имея по существу никакого обоснования. Эффективность его была поразительна и говорила сама за себя, но смысл дифференциала по-прежнему был неясен. Особенно часто путали бесконечно малое приращение функции и его линейную часть.

В течение всего XVIII века предпринимались грандиозные усилия для исправления положения, причём в них участвовали лучшие математики столетия, однако убедительно построить фундамент анализа удалось только Коши в начале XIX века. Он строго определил базовые понятия — предел, сходимость, непрерывность, дифференциал и др., после чего актуальные бесконечно малые исчезли из науки. Некоторые оставшиеся тонкости разъяснил позднее Вейерштрасс. В настоящее время термин «бесконечно малая» математики в подавляющем большинстве случаев относят не к числам, а к функциям и последовательностям.

Как иронию судьбы можно рассматривать появление в середине XX века нестандартного анализа, который доказал, что первоначальная точка зрения — актуальные бесконечно малые — также непротиворечива и могла бы быть положена в основу анализа. С появлением нестандартного анализа стало ясно, почему математики XVIII века, выполняя незаконные с точки зрения классической теории действия, тем не менее получали верные результаты.

См. также[править | править код]

  • «O» большое и «o» малое
  • Дифференциал (математика)
  • Метод неделимых
  • Предел последовательности
  • Предел функции

Примечания[править | править код]

  1. ↑ Бесконечно малые и бесконечно большие величины // Справочник по математике (для ср. уч. заведений)/ Цыпкин А. Г., под ред. Степанова С. А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 337—340. — 480 с.

Литература[править | править код]

  • Бесконечно малые и бесконечно большие величины // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Источник

Бесконечно малые величины и их свойства

Автор статьи

Щебетун Виктор

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Что такое бесконечно малая величина

Понятие бесконечно малой величины тесно связано с понятием предела.

Проследим изменение бесконечно малых на рисунках 1 и 2.

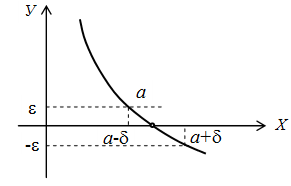
Функция y = f (x) пересекает ось Ох

Рисунок 1. Функция y = f (x) пересекает ось Ох

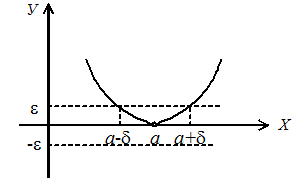
Функция y = f (x) касается оси Ох в точке х = а

Рисунок 2. Функция y = f (x) касается оси Ох в точке х = а

Что такое исчисление бесконечно малых величин

Вычисления с бесконечно малыми величинами, при которых результатом является бесконечно непрерывная сумма бесконечно малых, называют исчислением бесконечно малых величин.

Бесконечно малой последовательностью является такая последовательность an, для которой выполняется равенство:

[mathop{lim }limits_{nto infty } a_{n} =0]

Пример 1

Рассмотрим последовательность

[frac{1}{n} =frac{1}{2} ,frac{1}{3} ,frac{1}{4} …frac{1}{n} ]

Последовательность бесконечно убывает, а значит, является бесконечно малой величиной.

Функция называется бесконечно малой в окрестности точки х0, если выполняется условие:

[mathop{lim }limits_{nto x_{0} } f(x)=0]

Функция называется бесконечно малой на бесконечности, если выполняется одно из условий:

[mathop{lim }limits_{nto infty } f(x)=0; mathop{lim }limits_{nto -infty } f(x)=0]

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если:

$mathop{lim }limits_{nto infty } f(x)=a$, то

$f(x)-a=a(x)$ , $mathop{lim }limits_{nto infty } left(f(x)-aright)=0$

Бесконечно малая величина является переменной величиной, которая будет меньше числа $varepsilon $ лишь в результате своего стремления х к а.

[mathop{lim }limits_{nto a} f(x)=0]

«Бесконечно малые величины и их свойства» 👇

Определение

Функция y = f (x) называется бесконечно малой (при $x>+∞$), если каково бы ни было ${mathbf varepsilon } > 0$, можно найти такое число N, что при всех $x > N$ выполняется неравенство:

[left|f(x)right|

Пример 2

Доказать, что функция

[y=frac{1}{x^{2} } ]

является бесконечно малой при $x>+∞$.

Доказательство: Определим, что при $x>+∞$ предел функции b=0, т.е. что для любого $varepsilon > 0$ можно найти такое N, что при $x > N$ выполняется неравенство:

[left|f(x)right|=left|frac{1}{x^{2} } right|=frac{1}{x^{2} } Данное неравенство справедливо только если

[x>frac{1}{sqrt{varepsilon } } =N]

Аналогично для функции вида

$y=frac{1}{x^{a} } $ (а — любое положительное число)

Справедливо утверждение, что функция бесконечно малая.

Пример 3

Докажем, что функция $y = x^3$ является бесконечно малой при $x > 0$.

Доказательство: Зададим $varepsilon $ $>$ 0. Неравенство |f(x)| = |x3| $

[left|xright|Таким образом, неравенство $|x^3|

[N=-sqrt[{3}]{varepsilon } begin{array}{cc} {} & {begin{array}{cc} {8} & {M=sqrt[{3}]{varepsilon } } end{array}} end{array}]

Это значит, что

[mathop{lim }limits_{xto 0} x^{3} =0]

т.е. функция $y = x^3$ бесконечно малая при $x > 0$.

Пример 4

Определим, является ли бесконечно малой при $x > +∞$ функция:

[y=2-frac{1}{x} ]

Решение:

[mathop{lim }limits_{xto +infty } left(2-frac{1}{x} right)=2-0=2ne 0]

Ответ: Функция не является бесконечно малой при $x > +∞$.

Свойства бесконечно малых

  1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
  2. Произведение бесконечно малых — бесконечно малая.
  3. Произведение бесконечно малой последовательности на ограниченную (или константу) — бесконечно малая.
  4. Если $a_n$ — бесконечно малая последовательность, сохраняющая знак, то $b_n=1 / a_n$ — бесконечно большая последовательность.

Пример 5

Докажем, что функция

[y=frac{1}{x} +frac{1}{sqrt{x} } +frac{1}{x^{2} } ]

Является бесконечно малой функцией при $x > +∞$.

Доказательство: Так как каждое слагаемое функции является бесконечно малой при $x > +∞$ (см. пример 2), по свойству 1 — функция является бесконечно малой величиной.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 17.12.2022

Источник

Бесконечно малые величины.

Функция
называется бесконечно
малой
при
,
если
.

Примеры:

1)


функция

является бесконечно малой (б.м.) при
;

2)


функция

б.м. при
;

3)


функция

б.м. при
.

Бесконечно
малые функции часто называют бесконечно
малыми величинами или бесконечно малыми,
обозначают буквами α,
β,
γ,
δ
и
т.д. (В природе – масса льдины находящейся
в воде, в процессе таяния является
бесконечно малой величиной.) суть б.м.
в том, что в процессе изменения переменная
величина стремится к нулю.

Теорема
1.
Алгебраическая сумма любого конечного
числа бесконечно малых величин есть
так же бесконечно малая величина.

Теорема
2.
Произведение бесконечно малой функции


на ограниченную функцию

при

(или при
)
есть бесконечно малая функция.

Доказательство.
Так как функция

ограничена, то существует число М
такое, что при всех значениях x
из некоторой окрестности точки

.
Кроме того, так как

– бесконечно малая функция при
,
то для произвольного

найдется окрестность точки
,
в которой будет выполняться неравенство

.
Тогда в меньшей из этих окрестностей
имеем
.
А это и значит, что

– бесконечно малая. Для случая
доказательство проводится аналогично.

Из
доказанной теоремы вытекают:

Следствие
1.
Если
и

,
то
.
Произведение конечного числа б.м. величин
есть б.м. величина.

Следствие
2.
Если
и
c=const,
то
.
Произведение величины б.м. на величину
постоянную есть б.м. величина.

Теорема
3.
Отношение бесконечно малой функции

на функцию
,
предел которой отличен от нуля, есть
бесконечно малая функция.

Доказательство.
Пусть.
Тогда

есть ограниченная функция. Поэтому
дробь
есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.

Бесконечно большие функции.

Наряду
с бесконечно малыми величинами существуют
бесконечно большие. Например, время,
отсчитываемое от некоторого начального
момента, может возрастать неограниченно.
Путь, который проходит точка числовой
оси, неограниченно удаляясь от начала
координат.

Опр.
Функция

стремится к бесконечности при
,
т.е. является бесконечно
большой
величиной, если для любого числа М,
как бы велико оно ни было, можно найти
такое
,
что для всех значений
,
удовлетворяющих условию
,
имеет место неравенство
.

Обозначают

.

Если


стремится к бесконечности при

и при этом принимает только положительные
или только отрицательные значения,
соответственно пишут

или
.

П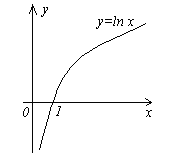римеры.

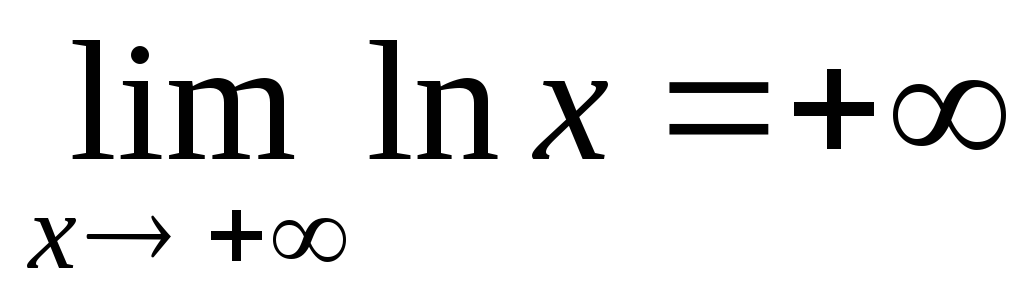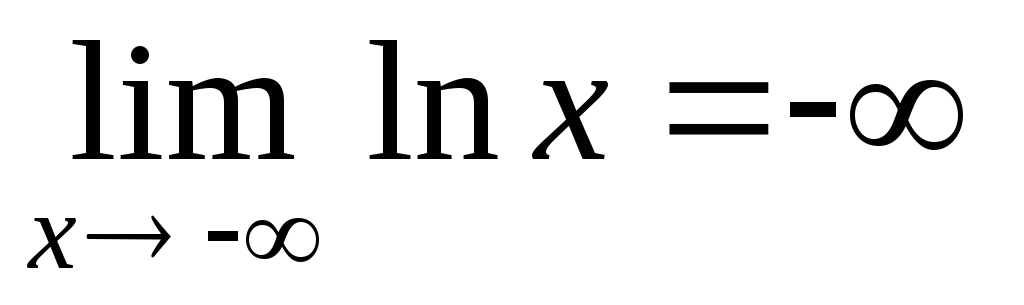  1. ,(см. рис.).

  1. .

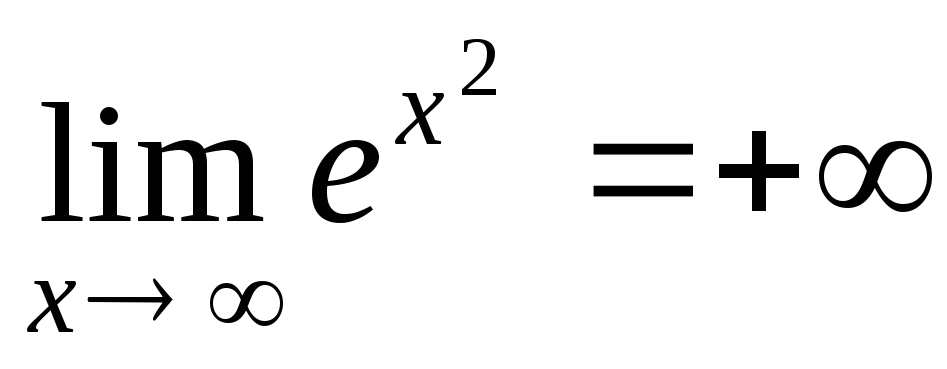
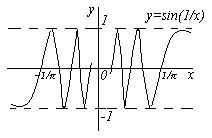  2. Функция
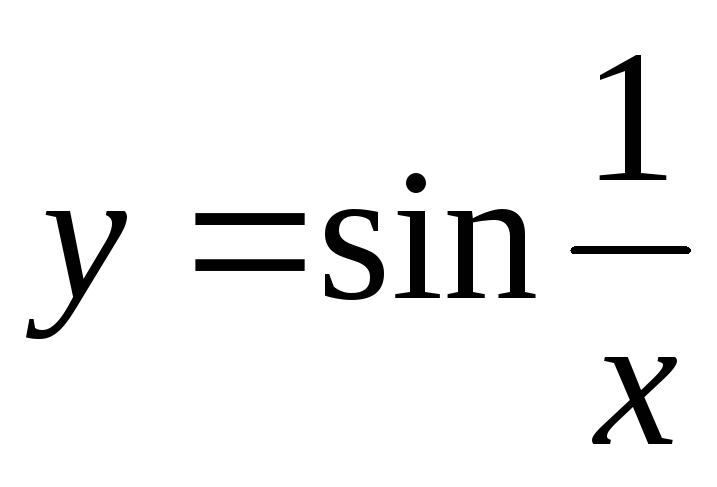
    при

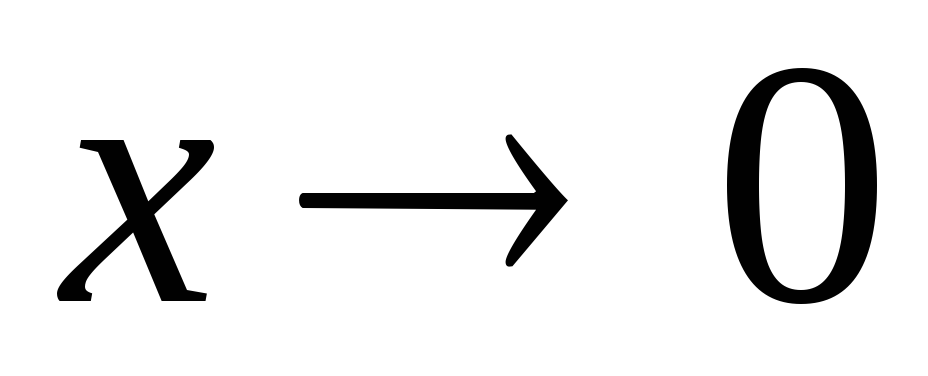
    не стремится ни к какому пределу (см.
    рис.).

Соотношение между бесконечно малыми и бесконечно большими функциями.

Теорема
1.
Если функция

является бесконечно большой при
,
то функция

является бесконечно малой при
.

Пример.

Ясно,
что при

функция


является бесконечно большой. Но тогда
согласно сформулированной выше теореме
функция
–
бесконечно малая при
,
т.е.
.

Теорема
2.
Если функция

– бесконечно малая при

(или)
и не обращается в нуль, то

является бесконечно большой функцией.

Примеры.

  1. .

  2. .

  3. ,
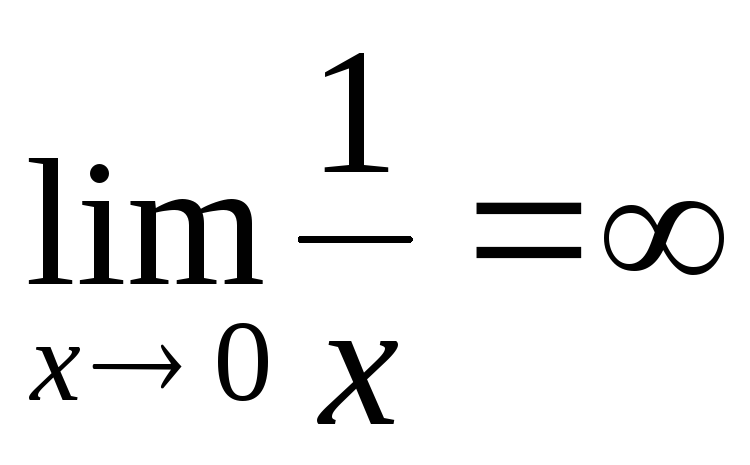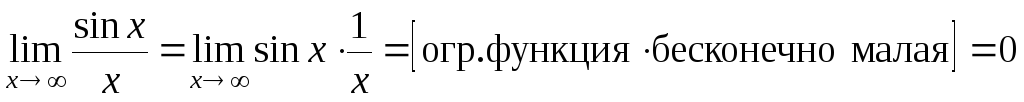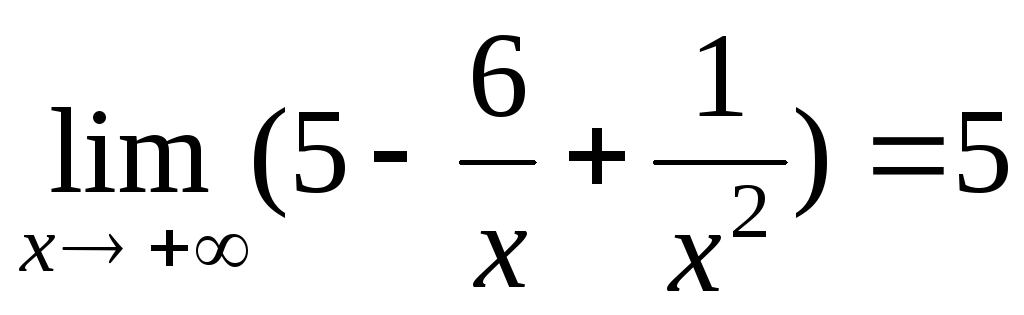    так как функци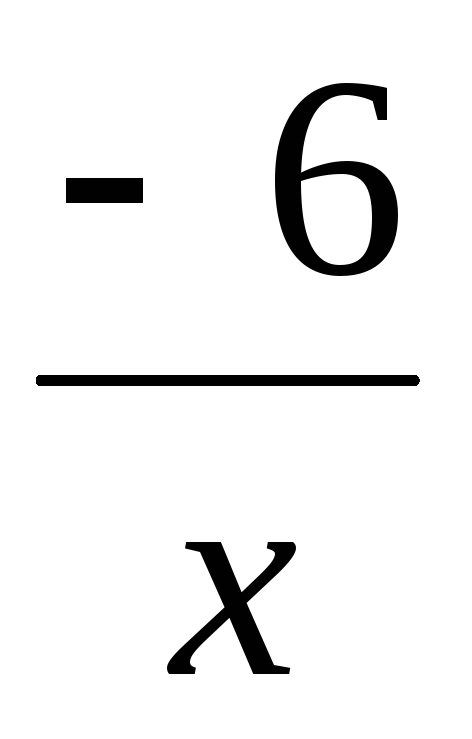и
    и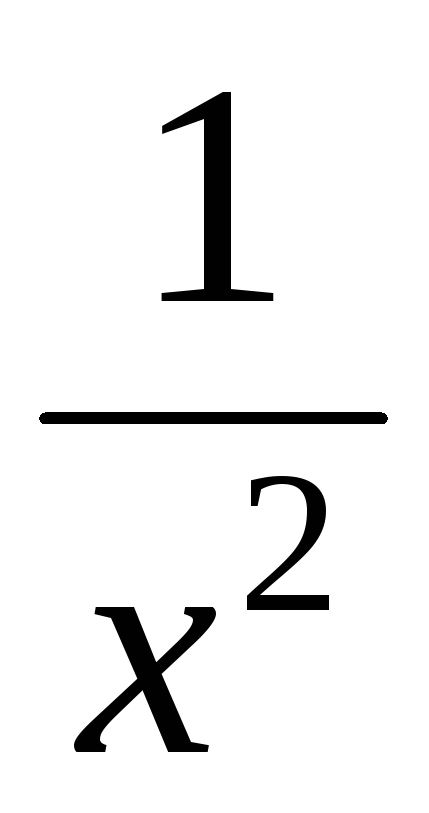

    –
    бесконечно малые при
    ,
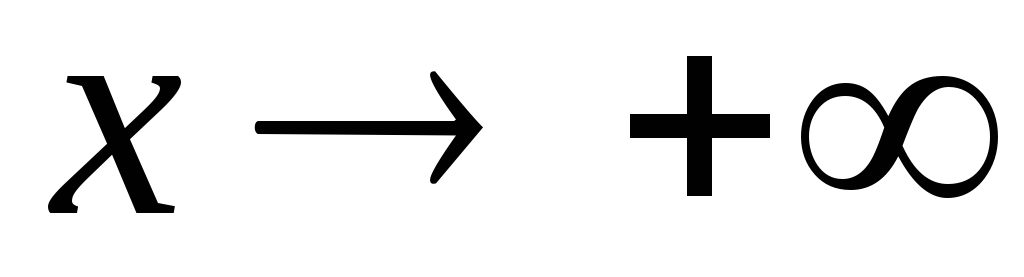    то
    ,
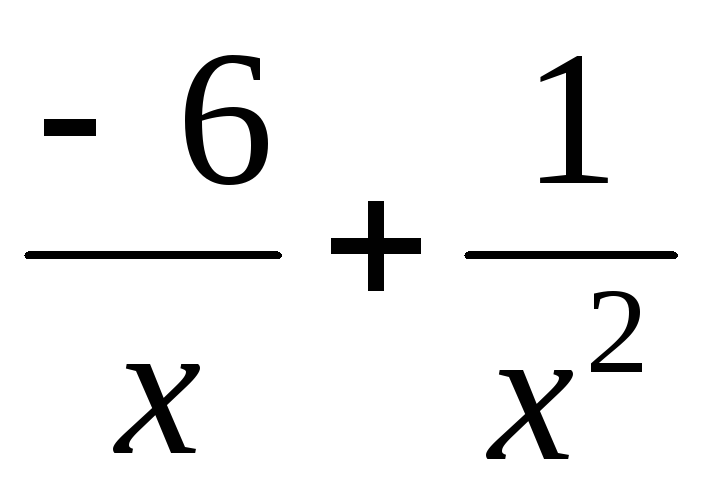    как сумма бесконечно малых функций
    есть функция бесконечно малая. Функция
    же

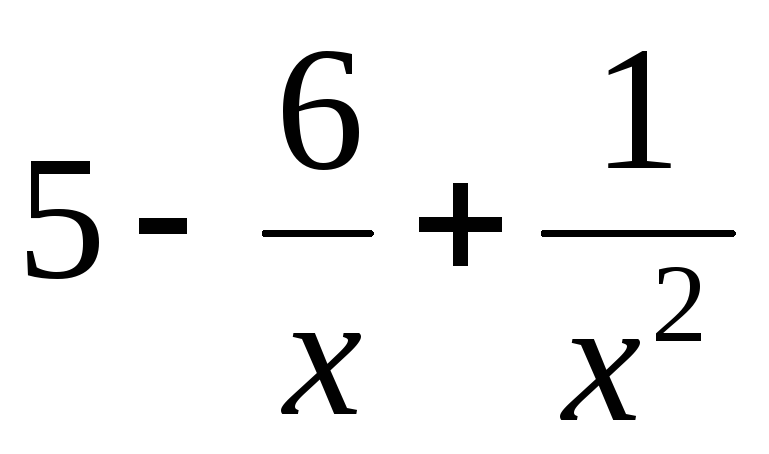
    является
    суммой постоянного числа и бесконечно
    малой функции. Следовательно, по теореме
    1 для бесконечно малых функций получаем
    нужное равенство.

Таким
образом, простейшие свойства бесконечно
малых и бесконечно больших функций
можно записать с помощью следующих
условных соотношений: A≠
0

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Исчисление бесконечно малых

Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.

Бесконечно малая

Последовательность {displaystyle a_{n}} называется бесконечно малой, если : {displaystyle lim _{nto infty }a_{n}=0}. Например, последовательность чисел {displaystyle a_{n}={frac {1}{n}}} — бесконечно малая.

Функция называется бесконечно малой в окресности точки {displaystyle x_{0}}, если {displaystyle lim _{xto x_{0}}f(x)=0}.

Теоремы о бесконечно малых

Бесконечно большая величина

Последовательность {displaystyle a_{n}} называется бесконечно большой, если : {displaystyle lim _{nto infty }a_{n}=infty }.

Функция называется бесконечно большой в окресности точки {displaystyle x_{0}}, если {displaystyle lim _{xto x_{0}}f(x)=infty }.

Сравнение бесконечно малых величин

Как сравнивать бесконечно малые величины(Неопределённости {displaystyle {frac {0}{0}}})?
Допустим, у нас есть бесконечно малые величины {displaystyle alpha (x)} и {displaystyle beta (x)} при {displaystyle xto a}.

Примеры

См. также

  • Предел последовательности
  • Предел функции
  • Дифференциал

ar:عدد لامتناهي
cs:Infinitezimální hodnota
gl:Infinitesimal
he:אינפיניטסימל
nl:Infinitesimaal
sv:Infinitesimal

Источник

Приветствую Вас, уважаемые Читатели! Понятие бесконечно малого прочно вошло в обиход математического анализа еще в 18 веке, когда Готфрид Лейбниц в своих работах впервые использовал обозначение “dx”. Но что он подразумевал под этим, как вообще можно определить что-то бесконечно малое?

Расскажу Вам о гениальном ходе, который перевернул стандартный математический анализ с ног на голову и стал отправным этапом для создания нового, инфинитезимального (нестандартного) анализа. Поехали!

Источник: https://projectvox.org/wp-content/uploads/2018/10/PE12_leibniz_denkmal_photo_hähnel_w1883_t1646_wikimedia_commons-943x1024.jpg
Источник: https://projectvox.org/wp-content/uploads/2018/10/PE12_leibniz_denkmal_photo_hähnel_w1883_t1646_wikimedia_commons-943×1024.jpg

Введение

Как можно подобраться к бесконечно малому числу? Для начала стоит произвести рекогносцировку и понять, где вообще существуют числа. Принято говорить, что все вещественные числа образуют поле – алгебраическую структуру, на которой определен ряд математических операций, которые при их применении, не выводят результат за рамки поля. Т.е. если два числа вещественные (например, 3,23 и -1/2), то и их сумма, их произведение, их обратные и противоположные элементы – суть элементы того же поля вещественных чисел.

Данное определение не претендует на строгость, но важно для понимания сути дальнейшего изложения.

Важным свойством поля вещественных чисел является выполнимость в нём аксиомы Архимеда:

Если имеются две отрезка a и b, причем a меньше b, то взяв a некоторое количество раз можно превзойти b.

Что такое бесконечно малое число ? Красивейший математический этюд

Вместо а можно взять число, например, единицу. Тогда любое вещественное число можно превзойти конечной суммой 1+1+1…+1, реализуя придуманный еще древнегреческим математиком Евдоксом метод исчерпываний.

Подходы к “бесконечной малости”

Первое определение, которое приходит на ум, когда речь идет о бесконечно малой величине – это ноль. Однако, это не так интересно, ведь нам хотелось бы найти такое число, которое ближе всех остальных к нулю на вещественной оси.

Что такое бесконечно малое число ? Красивейший математический этюд

Попытавшись задать ε как некое число, меньшее любого из вещественных, мы придём к бесконечной цепочке. Ведь, при рассмотрении поля, мы можем тогда вычислить и его элемент “ε/2” и т.д., которые будут еще меньше.

Таким образом в стандартном математическом анализе, понятие бесконечно малого – это некая цепочка, последовательность, имеющая предел, но не конкретное число!

Но есть интуитивный выход, результаты которого, Вы видели в каждом учебнике физики:

Здесь мы оперируем неким бесконечно малым изменением объема газа dV - конкретным, но очень маленьким числом, близким к нулю. Источник: http://900igr.net/up/datas/136682/023.jpg
Здесь мы оперируем неким бесконечно малым изменением объема газа dV – конкретным, но очень маленьким числом, близким к нулю. Источник: http://900igr.net/up/datas/136682/023.jpg

С этой точки зрения бесконечно малое число можно определить диаметрально противоположно. Пусть ε – некая величина. Начнём последовательно вычислять суммы: ε+ε, ε+ε+ε, ε+ε+ε+…ε и т.д.. Если окажется, что для любой конечной суммы будет выполняться неравенство ε+ε+ε+…ε < 1, такую величину определим как актуальное бесконечно малое число.

Слово “актуальное” здесь помогает нам отделить понятия бесконечно малого, как элемента последовательности, предела функций и т.д. до бесконечно малого, которое можно “пощупать”.

Отличное определение! Но постойте, этим самым мы нарушили кое-что важное, а именно аксиому Архимеда для поля вещественных чисел. Действительно, если взять отрезок длиной ε, то, сколько не укладывай его друг за другом, сумма не сможет покрыть даже отрезок единичной длины!

Добавлю, что бесконечно большое число определяется как 1/ε
Добавлю, что бесконечно большое число определяется как 1/ε

Что же получается? А то, что в поле вещественных чисел такого бесконечно малого ε существовать не может, ведь важнейшая аксиома для такого числа не выполняется, а значит оно не является вещественным.

Что же делают математики? Они расширяют поле вещественных чисел, добавляя в него новые элементы и получают поле уже гипервещественных чисел, в котором бесконечностями можно играть хоть и как песчинками, но вполне осязаемыми и реальными! Для этих чисел и создается новая область знаний – нестандартный (инфинитезимальный) анализ!

  • О гипервещественных числах читайте в моём материале!
  • TELEGRAM и Facebook – там я публикую не только интересные статьи, но и математический юмор и многое другое.
Источник

Добавить комментарий