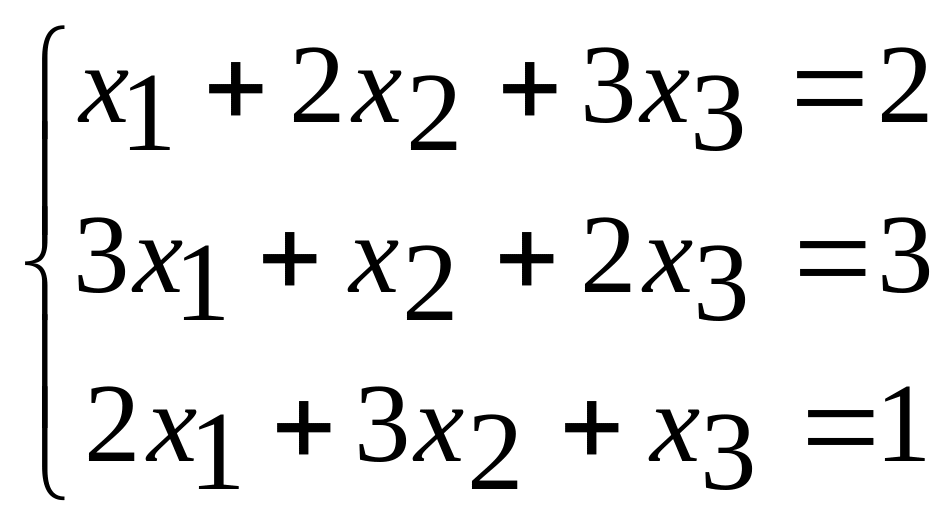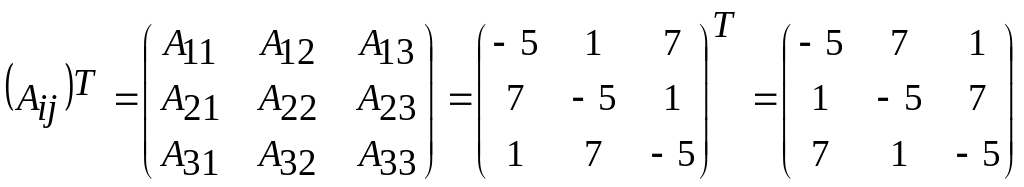Как найти бесконечное множество решений - Сайт, где вы сможете решить свои вопросы

Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.

Метод Гаусса

Метод Гаусса
1. Пример 1
2. Пример 2
Несовместность системы (нет решений)
1. Пример 3
Общее и частное решение системы (бесконечное множество решений)
1. Пример 4

Пусть задана система линейных алгебраических уравнений: $$begin{cases} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 = b_1 \ a_{21} x_1 + a_{22} x_2 + a_{23} x_3 = b_2 \ a_{31} x_1 + a_{32} x_2 + a_{33} x_3 = b_3 end{cases}. $$

Запишем систему уравнений в виде расширенной матрицы, состоящей из коэффициентов и столбца свободных членов. Вертикальная черта используется для удобства оформления. $$ begin{pmatrix} a_{11} & a_{12} & a_{13} & | & b_1 \ a_{21} & a_{22} & a_{23} & | & b_2 \ a_{31} & a_{32} & a_{33} & | & b_3 end{pmatrix} $$
С помощью элементарных преобразований матрицы (вычитание одной строки из другой, умноженной на коэффициент, удаление одинаковых и нулевых строк, деление строки на число отличное от нуля) получаем нули под главной диагональю $$ begin{pmatrix} a_{11} & a_{12} & a_{13} & | & b_1 \ 0 & a_{22} & a_{23} & | & b_2 \ 0 & 0 & a_{33} & | & b_3 end{pmatrix} $$
Используя элементарные преобразования, изложенные в пункте 2, приводим матрицу к виду содержащему нули везде, кроме главной диагонали $$ begin{pmatrix} a_{11} & 0 & 0 & | & b_1 \ 0 & a_{22} & 0 & | & b_2 \ 0 & 0 & a_{33} & | & b_3 end{pmatrix} $$

Пример 1

Решить систему уравнений методом Гаусса $$begin{cases} x_1 + 2 x_2 + x_3 = 5 \ -x_1 + 3 x_2 -2 x_3 = 3 \ – x_1 -7 x_2 + 4 x_3 = -5 end{cases}. $$

Решение

Запишем расширенную матрицу, состоящую из коэффициентов при неизвестных $x_1, x_2, x_3$ и отдельно столбец свободных членов $b_1, b_2, b_3$. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ -1 & 3 & -2 & | & 3 \ -1 & -7 & 4 & | & -5 end{pmatrix} $$

Приведем матрицу к нижнетреугольному виду (под главной диагональю должны быть нули) с помощью элементарных преобразований.

Прибавим ко второй строке первую. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ -1 & -7 & 4 & | & -5 end{pmatrix} $$

Далее прибавляем к третьей строке первую. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & -5 & 5 & | & 0 end{pmatrix}$$

Теперь осталось к третьей строке прибавить вторую строку, чтобы под главной диагональю были только нули. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & 0 & 4 & | & 8 end{pmatrix}$$

Замечаем, что в третьей строке стоят числа, которые можно сократить на четыре. Для этого выполняем деление всей третьей строки на 4. $$ begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & -1 & | & 8 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$

Теперь выполняем обратный ход Гаусса снизу вверх. Прибавляем ко второй строке третью строку. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 5 & 0 & | & 10 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$

Сразу замечаем, что вторую строку можно сократить на 5. $$begin{pmatrix} 1 & 2 & 1 & | & 5 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$

Продолжаем обратный ход, вычитаем третью строку из первой. $$begin{pmatrix} 1 & 2 & 0 & | & 3 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$

Осталось из первой строки вычесть вторую строку, умноженную на 2, для того, чтобы в первой строке появился ноль. $$begin{pmatrix} 1 & 0 & 0 & | & -1 \ 0 & 1 & 0 & | & 2 \ 0 & 0 & 1 & | & 2 end{pmatrix}$$

Теперь перепишем получившуюся матрицу в виде системы уравнений, чтобы в дальнейшем получить чему равны неизвестные $x_1, x_2, x_3$. $$begin{cases} x_1 = -1 \ x_2 = 2 \ x_3 = 2 end{cases}$$

Ответ

$$x_1 = -1, x_2 = 2, x_3 = 2$$

Пример 2

Решить систему линейных алгебраических уравнений методом Гаусса $$begin{cases} 2x_1 + 5 x_2 + 4x_3 + x_4 = 20 \ x_1 + 3 x_2 + 2x_3 +x_4 = 11 \ 2x_1 +10 x_2 + 9 x_3 + 7x_4 = 40 \ 3x_1 + 8x_2 + 9x_3 + 2x_4 = 37 end{cases}. $$

Решение

Записываем расширенную матрицу $$ begin{pmatrix} 2&5&4&1&|&20 \ 1&3&2&1&|&11 \ 2&10&9&7&|&40 \ 3&8&9&2&|&37 end{pmatrix}.$$

Умножаем вторую строку на 2 и вычитаем из неё первую строчку. Из третьей строки просто вычитаем первую. Умножаем четвертую строку на 2 и вычитаем из неё первую строку, умноженную на 3. Получаем матрицу $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&5&5&6&|&20 \ 0&1&6&1&|&14 end{pmatrix}.$$

Берем вторую строку, умноженную на 5 и вычитаем из третьей. Затем вторую строку вычитаем из четвертой. $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&6&0&|&12 end{pmatrix}$$

Теперь умножаем третью строку на 6 и вычитаем её из четвертой строки, умноженной на 5. $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&0&-6&|&0 end{pmatrix}$$

Получили нижнетреугольную матрицу, то есть ниже главной диагонали расположены нули. Теперь проделываем элементарные преобразования снизу вверх, так называемый обратный ход Гаусса. Но прежде замечаем, что появилась строка, в которой можно выполнить сокращение. А именно в четвертой строке можно разделить все числа на (-6). И получаем $$begin{pmatrix} 2&5&4&1&|&20 \ 0&1&0&1&|&2 \ 0&0&5&1&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$

Вот теперь вычитаем четвертую строчку из третьей, второй и первой. $$begin{pmatrix} 2&5&4&0&|&20 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$

Из второй строки мы не будем вычить третью, потому что там итак стоит ноль, ради которого мы проводим элементарные преобразования, поэтому пропускаем этот шаг.

Умножаем на 4 третью строку и вычитаем её из первой, умноженной на 5. $$begin{pmatrix} 10&25&0&0&|&60 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$

Замечаем, что в первой строке можно все числа сократить на 5. $$begin{pmatrix} 2&5&0&0&|&12 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$

Теперь остался последний шаг это умножить вторую строку на 5 и вычесть из первой. $$begin{pmatrix} 2&0&0&0&|&2 \ 0&1&0&0&|&2 \ 0&0&5&0&|&10 \ 0&0&0&1&|&0 end{pmatrix}$$

Замечаем, что первую строку можно сократить на 2, а третью строку на 5. $$begin{pmatrix} 1&0&0&0&|&1 \ 0&1&0&0&|&2 \ 0&0&1&0&|&2 \ 0&0&0&1&|&0 end{pmatrix}$$

Переписываем матрицу в виде привычной системы уравнений и получаем ответ $$begin{pmatrix} 1&0&0&0&|&1 \ 0&1&0&0&|&2 \ 0&0&1&0&|&2 \ 0&0&0&1&|&0 end{pmatrix} sim begin{cases} x_1 = 1 \ x_2 = 2 \ x_3 = 2 \ x_4 = 0 end{cases}.$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$x_1 = 1, x_2 = 2, x_3 = 2, x_4 = 0$$

Несовместность системы (нет решений)

Если в результате элементарных преобразований появилась нулевая строка вида $$begin{pmatrix} 0&0&0&|&b end{pmatrix} text{ где } b neq 0,$$то система уравнений не имеет решений. На этом алгоритм Гаусса заканчивает свою работу и можно записывать ответ, что система несовместна, то есть нет решений.

Пример 3

Найти решение системы линейных уравнений методом Гаусса $$begin{cases} 7x_1 – 2x_2 – x_3 = 2 \ 6x_1 – 4x_2 – 5x_3 = 3 \ x_1 + 2x_2 + 4x_3 = 5 end{cases}.$$

Решение

Как обычно пишем расширенную матрицу по коэффициентам при неизвестных переменных и столбцу свободных членов $$begin{pmatrix} 7&-2&-1&|&2 \ 6&-4&-5&|&3 \ 1&2&4&|&5 end{pmatrix}.$$

Запускаем алгоритм Гаусса. Идём сверху вниз. Умножаем вторую строку на 7 и вычитаем из неё первую строчку умноженную на 6. Затем первую строку вичитаем из третьей, умноженной на 7. $$begin{pmatrix} 7&-2&-1&|&2 \ 0&-16&-29&|&9 \ 0&16&29&|&33 end{pmatrix}$$

Далее по алгоритму прибавляем вторую строку к третьей. $$begin{pmatrix} 7&-2&-1&|&2 \ 0&-16&-29&|&9 \ 0&0&0&|&42 end{pmatrix}$$

Видим, что в результате элементарных преобразований появилась строка в которой все нули, кроме свободного члена. Это означает, что система несовместа, то есть у системы уравнений нет решения.

Ответ

Нет решений, так как система несовместна.

Общее и частное решение системы (бесконечное множество решений)

Часто после элементарных преобразований в расширенной матрице появляются нулевые строки вида $$begin{pmatrix} 0&0&0&|&0 end{pmatrix}.$$ Такую строку нужно вычеркивать из матрицы и система уравнений будет иметь бесконечное множество решений. Разберем это на практике.

Пример 4

Найти общее и два частных решения системы линейных алгебраических уравнений методом Гаусса $$begin{cases} x_1+x_2-x_3=4 \ 3x_1+2x_2-5x_3=7 \ 3x_1+x_2-7x_3=2 end{cases}.$$

Решение

Составляем расширенную матрицу $$begin{pmatrix} 1&1&-1&|&4 \ 3&2&-5&|&7 \ 3&1&-7&|&2 end{pmatrix}.$$

Из второй и третьей строки вычетаем первую, умноженную на 3. $$begin{pmatrix} 1&1&-1&|&4 \ 0&-1&-2&|&-5 \ 0&-2&-4&|&-10 end{pmatrix}$$

Из третьей строки вычитаем вторую, домноженную на 2. $$begin{pmatrix} 1&1&-1&|&4 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix}$$

Теперь согласно обратному ходу Гаусса вторую строку прибавляем к первой. $$begin{pmatrix} 1&0&-3&|&-1 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix}$$

По окочанию элементарных преобразований получилась строка, в которой все элементы равны нулю. Значит, система имеет бесконечное множество решений. Для его записи понадобится отличать базисные и свободные переменные. Обычно за базисные берут переменные, которые стоят на главной диагонали, а остальные свободные. В нашем случае базисными будут $x_1, x_2$, а свободной $x_3$.

Переписываем матрицу в виде системы $$begin{pmatrix} 1&0&-3&|&-1 \ 0&-1&-2&|&-5 \ 0&0&0&|&0 end{pmatrix} sim begin{cases} x_1-3x_3 = -1 \ -x_2-2x_3 = -5 end{cases}.$$

Так как $x_1, x_2$ являются базисными переменными, то их переносим в левую часть равенства, а всё остальное в правую часть. Получившееся называют общим решением решением системы уравнений $$begin{cases} x_1-3x_3 = -1 \ -x_2-2x_3 = -5 end{cases} sim begin{cases} x_1 = 3x_3-1 \ x_2 = 5-2x_3 end{cases}.$$

Чтобы получить частное решение системы уравнений нужно вместо свободного $x_3$ подставить любое число, например $x_3 = 0$. Тогда получаем, что $$begin{cases} x_1 = -1 \ x_2 = 5 end{cases}.$$ Возьмем ещё например $x_3 = 1$ и получаем $$begin{cases} x_1 = 2 \ x_2 = 3 end{cases}.$$

Можно брать различные числа вместо $x_3$ и получать бесконечное множество решений.

Ответ

Общее решение системы уравнений $$begin{cases} x_1 = 3x_3-1 \ x_2 = 5-2x_3 end{cases}.$$

Частные решения системы уравнений $$begin{cases} x_1 = -1 \ x_2 = 5 end{cases}, begin{cases} x_1 = 2 \ x_2 = 3 end{cases}.$$

Источник

1. Системы линейных уравнений с параметром

Системы линейных уравнений с параметром решаются теми же основными методами, что и обычные системы уравнений: метод подстановки, метод сложения уравнений и графический метод. Знание графической интерпретации линейных систем позволяет легко ответить на вопрос о количестве корней и их существовании.

Пример 1.

Найти все значения для параметра а, при которых система уравнений не имеет решений.

{х + (а² – 3)у = а,
{х + у = 2.

Решение.

Рассмотрим несколько способов решения данного задания.

1 способ. Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов (а/а₁ = b/b₁ ≠ c/c₁). Тогда имеем:

1/1 = (а² – 3)/1 ≠ а/2 или систему

{а² – 3 = 1,
{а ≠ 2.

Из первого уравнения а² = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.

Ответ: а = -2.

2 способ. Решаем методом подстановки.

{2 – у + (а² – 3)у = а,
{х = 2 – у,

или

{(а² – 3)у – у = а – 2,
{х = 2 – у.

После вынесения в первом уравнении общего множителя у за скобки, получим:

{(а² – 4)у = а – 2,
{х = 2 – у.

Система не имеет решений, если первое уравнение не будет иметь решений, то есть

{а² – 4 = 0,
{а – 2 ≠ 0.

Очевидно, что а = ±2, но с учетом второго условия в ответ идет только ответ с минусом.

Ответ: а = -2.

Пример 2.

Найти все значения для параметра а, при которых система уравнений имеет бесконечное множество решений.

{8х + ау = 2,
{ах + 2у = 1.

Решение.

По свойству, если отношение коэффициентов при х и у одинаковое, и равно отношению свободных членов системы, то она имеет бесконечное множество решений (т. е. а/а₁ = b/b₁ = c/c₁). Следовательно 8/а = а/2 = 2/1. Решая каждое из полученных уравнений находим, что а = 4 – ответ в данном примере.

Ответ: а = 4.

2. Системы рациональных уравнений с параметром

Пример 3.

Найти все значения параметра а, при которых система уравнений имеет единственное решение.

{3|х| + у = 2,
{|х| + 2у = a.

Решение.

Умножим первое уравнение системы на 2:

{6|х| + 2у = 4,
{|х| + 2у = a.

Вычтем из первого второе уравнение, получим 5|х| = 4 – а. Это уравнение будет иметь единственное решение при а = 4. В других случаях это уравнение будет иметь два решения (при а < 4) или ни одного (при а > 4).

Ответ: а = 4.

Пример 4.

Найти все значения параметра а, при которых система уравнений имеет единственное решение.

{х + у = а,
{у – х² = 1.

Решение.

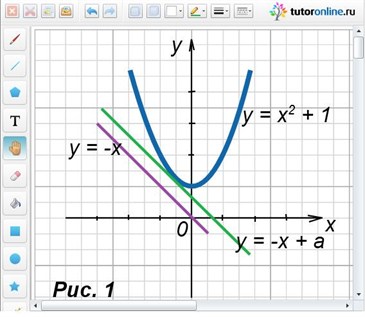
Данную систему решим с использованием графического метода. Так, графиком второго уравнения системы является парабола, поднятая по оси Оу вверх на один единичный отрезок. Первое уравнение задает множество прямых, параллельных прямой y = -x (рисунок 1). Из рисунка хорошо видно, что система имеет решение, если прямая у = -х + а является касательной к параболе в точке с координатами (-0,5; 1,25). Подставив в уравнение прямой вместо х и у эти координаты, находим значение параметра а:

1,25 = 0,5 + а;

а = 0,75.

Ответ: а = 0,75.

Пример 5.

Используя метод подстановки, выясните, при каком значении параметра а, система имеет единственное решение.

{ах – у = а + 1,
{ах + (а + 2)у = 2.

Решение.

Из первого уравнения выразим у и подставим во второе:

{у = ах – а – 1,
{ах + (а + 2)(ах – а – 1) = 2.

Приведем второе уравнение к виду kx = b, которое будет иметь единственное решение при k ≠ 0. Имеем:

ах + а²х – а² – а + 2ах – 2а – 2 = 2;

а²х + 3ах = 2 + а² + 3а + 2.

Квадратный трехчлен а² + 3а + 2 представим в виде произведения скобок

(а + 2)(а + 1), а слева вынесем х за скобки:

(а² + 3а)х = 2 + (а + 2)(а + 1).

Очевидно, что а² + 3а не должно быть равным нулю, поэтому,

а² + 3а ≠ 0, а(а + 3) ≠ 0, а значит а ≠ 0 и ≠ -3.

Ответ: а ≠ 0; ≠ -3.

Пример 6.

Используя графический метод решения, определите, при каком значении параметра а, система имеет единственное решение.

{х² + у² = 9,
{у – |х| = а.

Решение.

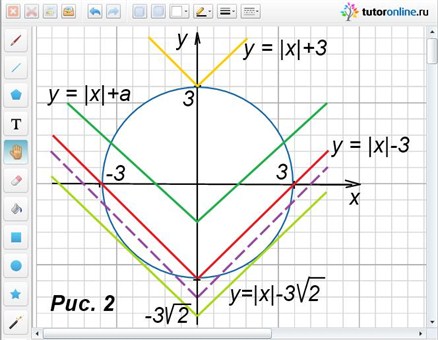
Исходя из условия, строим окружность с центром в начале координат и радиусом 3 единичных отрезка, именно ее задает первое уравнение системы

х² + у² = 9. Второе уравнение системы (у = |х| + а) – ломаная. С помощью рисунка 2 рассматриваем все возможные случаи ее расположения относительно окружности. Легко видеть, что а = 3.

Ответ: а = 3.

Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

Источник

Как подобрать такое значение чтобы система уравнений имела бесконечно много решений?

evskroh

Ученик

(232),
на голосовании

4 года назад

Система уравнений:
3x + y = 5
ax +3y= c

Голосование за лучший ответ

Mister User

Оракул

(58260)

5 лет назад

Два уравнения – это две прямых. Чтобы система уравнений имела бесконечно много решений, прямые должны совпадать одна с другой. Тогда любая пара х и у подойдет к одной и ко второй. Чтоб прямые совпадали, у них должен быть одинаковый угловой коэффициент (множитель при х), и одинаковый свободный член.
у = kx + b
Вырази у через х и приравняй k и b.

y = -3x + 5
y = -ax/3 + с/3

-3x =-aх/3
а = 9

5 = с/3
с = 15

Источник

Пример
4. Решить
систему линейных уравнений

_.

Решение.
Составим определитель из коэффициентов
при неизвестных и вычислим его:

,
значит, СЛУ имеет единственное решение.
Найдем вспомогательные определители
и значения неизвестных.

Ответ:

.

Рассмотрим пример,
в котором СЛУ
имеет бесконечное множество решений,
и они будут найдены с применением формул
Крамера.

Пример
5.
Решить СЛУ.

Решение.

Вычислим
определитель системы:

Заметим,
что третье уравнение системы равно
сумме первых двух уравнений, т.е. зависит
от первых двух уравнений. Отбросив
третье уравнение, получим равносильную
систему двух уравнений с тремя
неизвестными:

Оставим
в левой части системы те неизвестные,
коэффициенты при которых образуют
определитель, не равный нулю, например,

.
Неизвестное

является
свободным,
а неизвестные

и

– базисными
неизвестными.
Запишем систему в виде

и применим
к ней правило Крамера:

;

–
общее
решение
неопределенной СЛУ, где

– любое действительное число.

Из
общего решения можно получить частные
решения,
если придать свободной неизвестной
какое-то конкретное значение. Например,
пусть

,
тогда

;
частное решение

.

3. Матричный метод решения слу

3.1. Матричная запись системы линейных уравнений

Пусть

– матрица коэффициентов при неизвестных,

– матрица-столбец неизвестных,

– матрица-столбец свободных членов.
Система

уравнений с

неизвестными в матричном виде запишется
как

(матричное уравнение системы):

3.2. Решение системы уравнений с помощью обратной матрицы

Умножив
обе части уравнения

системы на обратную матрицу

слева и
используя свойство

,
получим выражение для матрицы неизвестных

.
Оно показывает, как найти решение
системы

линейных уравнений с

неизвестными с помощью обратной матрицы.

Пример
6. Решить с
помощью обратной матрицы систему
уравнений

Решение.
Вычислим определитель:

.
Так как

,
то система уравнений имеет единственное
решение

.

2)
Составим обратную матрицу. Матрица

существует, т.к. определитель

.
Найдем алгебраические дополнения

.

,

,

,

,

,

.

Составим
матрицу из алгебраических дополнений

и транспонируем ее.

.

Разделим
каждый элемент этой матрицы на определитель

,
получим искомую обратную матрицу:

.

3)
Матрица неизвестных

равна произведению матрицы

на матрицу свободных членов

:

Вычислим
значения неизвестных:

,

,

.

Ответ.
Система имеет единственное решение

.

4. Сущность метода исключения неизвестных (метода Гаусса). Элементарные преобразования

Сущность
метода Гаусса
состоит в том, что система линейных
уравнений с помощью элементарных
преобразований приводится к равносильной
системе треугольного или трапецеидального
вида, из которой легко находится решение
системы или делается вывод о несовместности
системы. Метод Гаусса применяется к
любой СЛУ,
в которой число уравнений равно числу
неизвестных, или больше числа неизвестных,
или меньше числа неизвестных.

К элементарным преобразованиям над
уравнениями системы относятся:

Перестановка
уравнений местами.
Умножение уравнения
на число, не равное нулю.
Прибавление одного
уравнения к другому уравнению, умноженному
на какое-либо число.
Отбрасывание
одинаковых уравнений (кроме одного), а
также уравнения вида

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 ноября 2021 года; проверки требуют 3 правки.

Бесконечная система линейных алгебраических уравнений — обобщение понятия системы линейных алгебраических уравнений на случай бесконечного множества неизвестных, определённое методами функционального анализа. Оно имеет смысл не над любым полем, а, например, над вещественными и комплексными числами. Также возможно прямолинейное обобщение методами собственно линейной алгебры, отличное от описанного в статье.

Бесконечная система линейных алгебраических уравнений часто появляется в процессе решения разнообразных задач в физике и технике методом неопределённых коэффициентов, например в задачах теплопроводности, определения перигелия движения Луны в астрономии, в задаче определения статического прогиба прямоугольного тела с закреплёнными концами.^[1]

Определение[править | править код]

Бесконечной системой линейных алгебраических уравнений называется бесконечное множество алгебраических уравнений первой степени относительно бесконечного множества неизвестных: ${displaystyle sum _{k=1}^{infty }a_{ik}x_{k}=b_{i}}$ , . Решением бесконечной системы линейных алгебраических уравнений называется всякая последовательность чисел ${displaystyle left{x_{k}right}}$ , такая, что все ряды ${displaystyle sum _{k=1}^{infty }a_{ik}x_{k}}$ , являются сходящимися к $b_{{i}}$ . Решение ${displaystyle left{x_{k}right}}$ бесконечной системы линейных алгебраических уравнений называется ограниченным, если числа $x_{k}$ образуют ограниченную последовательность.

Удобно рассматривать бесконечные системы линейных алгебраических уравнений в виде: ${displaystyle x_{i}-sum _{k=1}^{infty }c_{ik}x_{k}=b_{i}}$ , , ${displaystyle c_{ik}=-a_{ik}+delta _{ik}}$ . Бесконечная система линейных алгебраических уравнений называется вполне регулярной, если существует такая положительная постоянная q<1 , что ${displaystyle sum _{k=1}^{infty }left|c_{ik}right|leqslant q}$ .

Вполне регулярная бесконечная система линейных алгебраических уравнений имеет единственное ограниченное решение ${displaystyle left{x_{i}right}}$ при любой ограниченной совокупности свободных членов $b_{{i}}$ . При этом, если ${displaystyle b_{i}leqslant B}$ для всех , то ${displaystyle left|x_{i}right|leqslant {frac {B}{1-q}}}$ .^[2]

Бесконечный определитель[править | править код]

В матрице коэффициентов бесконечной линейной системы уравнений можно оставить лишь первые строк и столбцов и составить из них квадратную матрицу размером :

${displaystyle A(n)={begin{vmatrix}a_{11}&a_{12}&cdots &a_{1n}\a_{21}&a_{22}&cdots &a_{2n}\cdots &cdots &cdots &cdots \a_{n1}&a_{n2}&cdots &a_{nn}end{vmatrix}}}$

Обозначим определитель этой матрицы как .

Если существует предел: ${displaystyle Delta =lim _{nto infty }Delta (n)}$ , то он называется бесконечным определителем, соответствующим матрице $a_{{ij}}$ ^[3].

Достаточное условие существования[править | править код]

Представим матрицу ${displaystyle a_{ij}}$ в новом виде, выделив из её всех диагональных членов слагаемое, равное единице:

${displaystyle a_{ij}={begin{vmatrix}a_{11}&a_{12}&cdots \a_{21}&a_{22}&cdots \cdots &cdots &cdots end{vmatrix}}={begin{vmatrix}c_{11}+1&c_{12}&cdots \c_{21}&c_{22}+1&cdots \cdots &cdots &cdots end{vmatrix}}}$

Для того, чтобы бесконечный определитель матрицы $a_{{ij}}$ существовал и обладал свойствами, аналогичными свойствам обычного определителя, достаточно, чтобы бесконечный двойной ряд ${displaystyle sum _{i,k=1}^{infty }|c_{ik}|}$
сходился.^[3]

Решение бесконечной системы линейных алгебраических уравнений[править | править код]

Если у матрицы $a_{{ij}}$ бесконечной системы линейных алгебраических уравнений существует и не равен нулю бесконечный определитель и все её свободные члены ограничены по модулю (то есть существует положительное число $M_{1}$ , такое, что ${displaystyle |b_{k}|<M_{1},forall k}$ ), то эта система имеет единственное ограниченное решение (то есть существует положительное число $M_{2}$ , такое, что ${displaystyle |x_{k}|<M_{2},forall k}$ ), определяемое по формулам Крамера:

${displaystyle x_{k}={frac {Delta _{k}}{Delta }}}$

где ${displaystyle Delta _{k}}$ — определитель, который получается из определителя Delta заменой элементов k-го столбца свободными членами.^[4]

См. также[править | править код]

Система линейных алгебраических уравнений

Примечания[править | править код]

↑ Смирнов, 1933, с. 57-61.
↑ Вулих, 1958, с. 215—218.
↑ ¹ ² Смирнов, 1933, с. 64.
↑ Смирнов, 1933, с. 65.

Литература[править | править код]

Вулих Б.З. Введение в функциональный анализ. — М.: Физматлит, 1958. — 352 с. — 7500 экз.
Смирнов В. И. Курс высшей математики для техников и физиков. Том 3. — М.: Гостехтеориздат, 1933. — 736 с. — 22 000 экз.

Источник

Метод Гаусса

Несовместность системы (нет решений)

Общее и частное решение системы (бесконечное множество решений)

Как подобрать такое значение чтобы система уравнений имела бесконечно много решений?

3. Матричный метод решения слу

3.1. Матричная запись системы линейных уравнений

3.2. Решение системы уравнений с помощью обратной матрицы

4. Сущность метода исключения неизвестных (метода Гаусса). Элементарные преобразования

Определение[править | править код]

Бесконечный определитель[править | править код]

Достаточное условие существования[править | править код]

Решение бесконечной системы линейных алгебраических уравнений[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как найти работу водителем в челябинске

Как составить рассылку по электронной почте

Как найти кабель в земле прибор

Добавить комментарий Отменить ответ