Бесконе́чность — категория человеческого мышления, используемая для характеристики безграничных, беспредельных, неисчерпаемых предметов и явлений, для которых невозможно указание границ или количественной меры[1]. Используется в противоположность конечному, исчисляемому, имеющему предел. Систематически исследуется в математике[⇨], логике[⇨] и философии[⇨], также изучаются вопросы о восприятии, статусе и природе бесконечности в психологии, теологии, физике[⇨] соответственно. Бесконечность обозначается символом 
Исторически первые проблемы бесконечности — вопросы конечности пространства и времени, количества вещей в мире, более сложные проблемы — возможность бесконечного деления континуума[⇨], возможность оперирования с бесконечными объектами (проблема актуальной бесконечности[⇨]), природа и поведение бесконечно малых величин — инфинитезималей[⇨], наличие различных типов бесконечности и соотношение между ними[1]. Наиболее глубокое исследование бесконечности предпринято в математической теории множеств[⇨], в которой построено несколько систем измерений различных видов бесконечных объектов, однако без дополнительных искусственных ограничений такие построения вызывают многочисленные парадоксы[⇨], пути их преодоления, статус теоретико-множественных построений, их обобщений и альтернатив являются основным направлением исследований бесконечности у философов современности[⇨].
Основные понятия[править | править код]
Потенциальная и актуальная бесконечность[править | править код]
Бесконечность может рассматриваться как неограниченность некоторого процесса, например, когда во втором постулате Евклида утверждается возможность продолжить бесконечно и непрерывно любую прямую, то имеется в виду, что процесс можно непрерывно продолжать, но существование такого самостоятельного объекта, как бесконечная прямая, из него не следует. Такого рода процессы и совокупности объектов, их описывающие, характеризуют как потенциальную бесконечность (в схоластике используется термин «синкатегорематическая бесконечность»), потенциально бесконечное не подразумевает целостных бесконечных предметов и явлений, в каждой фазе бесконечного процесса рассматриваются лишь конечные сущности, то есть является лишь частичным отрицанием конечного[1].
Альтернативой является понятие актуальной бесконечности (в схоластике — «категорематическая бесконечность»), которая означает рассмотрение конечно неизмеримых объектов как данность, как реально существующих, но при этом как единых и целостных, с которыми возможно оперировать[1]. В таком ключе актуально бесконечное — как прямое и полное отрицание конечного — используют мистики для характеризации различных божественных категорий, математики современности оперируют с актуально бесконечными множествами[⇨] и актуально бесконечномерными пространствами[⇨]. Представления о допустимости и содержании актуальной бесконечности в философии, теологии, логике, математике, естествознании существенно менялись на протяжении всего времени рассмотрения вопроса.
Качественная и количественная бесконечность[править | править код]
Качественная бесконечность — категория, определяющая всеобщий, неиссякаемый, универсальный характер связей объектов и явлений[2], как качественно бесконечные рассматриваются в различные времена в различных философских школах такие категории, как Абсолют, Космос, Бог, Ум и другие.
Количественная бесконечность характеризует процессы и объекты, измерение которых невозможно конечными величинами, с количественной бесконечностью оперируют математики, изучая, например, свойства бесконечных рядов, бесконечномерные пространства, множества из бесконечного количества элементов; в логике и философии исследуются возможности и ограничения такой работы с количественной бесконечностью.
Континуум[править | править код]
Континуум (лат. continuum) — форма бесконечности, относящаяся к идее о непрерывности, целостности объектов в смысле возможности бесконечного их разделения на составные части и потенциальной бесконечности этого процесса. Континуальность противопоставляется дискретности, прерывистости, наличию неделимых (атомарных) составляющих. Континуумом представляются отрезки числовой оси (континуум в теории множеств), определённый вид ограниченных и отделимых пространств, в некотором смысле сходных с отрезками числовой оси (континуум в топологии), на основе исследования свойств бесконечной делимости континуума в математике сформировано понятие непрерывности. Вопросы об онтологической природе континуума, статусе континуума в естествознании нашли отражение во многих трудах философов, начиная со времён античности[3].
Инфинитезималь[править | править код]
Инфинитезимали — бесконечно малые величины, фигурирующие в потенциально бесконечных процессах, характеризующихся последовательным убыванием величин, в частности, при разделении континуума на составные части, в убывающих числовых последовательностях, иногда — в представлении об атомарной структуре мироздания или сознания. Математическое описание инфинитезималей, созданное Ньютоном и Лейбницем в исчислении бесконечно малых[⇨], стало базисом математического анализа[4].
В математике[править | править код]
Теория чисел[править | править код]
Одним из основных источников ранних представлений о бесконечности были натуральные числа и потенциальная бесконечность натурального ряда. Одним из первых нетривиальных результатов о бесконечности в теории чисел считается доказательство от противного бесконечности множества простых чисел в «Началах» Евклида[5]: если предположить конечность множества простых чисел, то число, равное сумме единицы и произведения всех чисел из этого множества, не делится ни на одно из них, но при этом или само является простым, или делится на некоторое простое число, не входящее в исходное множество; и то, и другое противоречит исходной посылке. Теоретико-числовое суждение о бесконечности представляет парадокс Галилея: каждому числу может быть сопоставлен его квадрат, то есть, квадратов не меньше, чем всех чисел, но при этом не из каждого числа можно извлечь корень, то есть, квадраты — только часть множества всех чисел[6].
В теории чисел не требуется применение какой-либо абстракции актуальной бесконечности, тем не менее, многие её задачи связаны с формулировкой условий бесконечности, например, по состоянию на 2019 год являются открытыми проблемами вопросы о бесконечности множества простых чисел, по модулю которых заданное целое число является первообразным корнем (гипотеза Артина), бесконечности множества простых чисел-близнецов, бесконечности для всякого чётного числа множества пар соседних простых чисел, разность между которыми равна ему (гипотеза Полиньяка), бесконечности множества совершенных чисел.
Бесконечные ряды[править | править код]
Первое свидетельство применения бесконечного ряда обнаруживается у Архимеда в «Квадратуре параболы», где для доказательства утверждения о соотношении 4:3 площадей сегмента, заключённого между прямой и параболой, и треугольника, имеющего с ним то же основание и равную высоту, он суммирует бесконечный ряд:
,
и затем перепроверяет результат методом от противного[7].
В 1340-е годы Суайнсхед впервые находит сумму бесконечного ряда, не являющегося простой убывающей геометрической прогрессией:
.
Также в XIV веке с бесконечными рядами работает Орем, используя ясные геометрические доказательства, он получает суммы достаточно нетривиальных числовых рядов, находит (без доказательства) формулу суммы бесконечной геометрической прогрессии и доказывает расходимость гармонического ряда[7].
В XVI веке, используя результаты Орема, Томаш[de] находит суммы некоторых бесконечных прогрессий, образованных сложными законами[7]. В Индии в XV веке были получены разложения тригонометрических функций в бесконечные степенные ряды[7], наиболее значительный вклад внёс Мадхава из Сангамаграмы[8].
Менголи в трактате, опубликованном в 1650 году устанавливает ряд важных свойств рядов, вводит понятие остатка ряда, тем самым неявно рассматривая ряды как целостные объекты, а также доказывает расходимость обобщённого гармонического ряда[9]. Меркатор в 1668 году открывает разложение логарифмической функции в степенной ряд[10], а в 1667 году Грегори — разложения тригонометрических функций, и, наконец, Тейлор, обобщая результаты Меркатора, Грегори, а также Ньютона, в 1715 году показывает возможность разложить в бесконечный ряд любую аналитическую функцию в заданной точке, тем самым установив возможность представления значений обширного класса функций бесконечными суммами.
Исчисление бесконечно малых[править | править код]
Хотя метод исчерпывания, известный со времён античности, и метод неделимых, сформулированный Кавальери в 1635 году, в той или иной мере используют сведение к бесконечно малым величинам, первые попытки алгебраизации операций с бесконечно малыми были сделаны Валлисом, Барроу и Грегори в середине XVII века, в явном виде математическая абстракция инфинитезималей была создана в 1680-е годы практически одновременно Ньютоном в его «методе флюксий» (бесконечно малых приращений) и Лейбницем (определившим дифференциал)[4].
Строгие определения бесконечно малых с использованием понятий предела, сходимости и непрерывности даны в XIX веке Коши и Вейерштрассом, наиболее традиционной в этих определениях стала так называемая 









В нестандартном анализе Робинсона (1960-е годы) бесконечно малые вводятся как вид обобщённых чисел, не превосходящих 


Математический анализ[править | править код]
В математическом анализе, созданном на фундаменте исчисления бесконечно малых[⇨], вводится явно и абстракция бесконечно больших величин: ко множеству действительных чисел добавляются символы бесконечно удалённых точек 



,
,
,
,
,
,
,
,
,
однако с некоторыми ограничениями: при возникновении неопределённых ситуаций
применяются правила раскрытия неопределённостей (например, правило Лопиталя) по принципу выяснения содержания предельного выражения, приведшего к появлению бесконечности, то есть, в этом смысле в анализе символы 

В нестандартном анализе Робинсона бесконечно большие и бесконечно малые величины актуализируются с привлечением теоретико-модельных средств, причём выразительные средства и методы доказательств благодаря этому в нестандартном анализе во многих случаях выигрывают перед классическими, и получен ряд новых результатов, которые могли бы быть получены и в классическом анализе, но не были обнаружены из-за недостатка наглядности[13].
Проективная геометрия[править | править код]
Важным в актуализации представлений о бесконечности в математике стало создание Понселе в 1822 году проективной геометрии, одной из ключевых идей которой является сворачивание при проектировании бесконечно удалённого в «идеальные точки» и «идеальные прямые». Так, чтобы превратить бесконечную плоскость в евклидовом пространстве 


Так же, как и в анализе[⇨], с полученной бесконечностью в проективной геометрии можно оперировать (в проективной геометрии, в отличие от анализа, бесконечность не имеет знака, 
,
,
,
,
,
,
но при этом выражения 
Создавая геометрическую интерпретацию комплексных чисел, Риман в 1851 году воспользовался средствами проективной геометрии, и для комплексной плоскости 





Теория множеств[править | править код]
Основной вклад в представление о бесконечности в математике внесён теорией множеств: идея актуальной бесконечности и разных сортов бесконечности занимают существенную часть этой теории.
Для измерения разных видов бесконечности в теории множеств вводится понятие мощности (кардинального числа), совпадающее с количеством элементов для конечных множеств, а для бесконечных множеств задействующее принцип биекции: если между множествами возможно установить взаимно-однозначное соответствие, то они равномощны. Так, оказывается, что множество натуральных чисел 


![mathbb I = [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dde877d72cff66b34f632b167b4f526ffd01e1c1)












Представление порядковых чисел до 
Другой вид бесконечностей, введённый теорией множеств — порядковые числа (ординалы), наряду со связанным с ними принципом трансфинитной индукции они вызвали наибольшие дискуссии в среде математиков, логиков и философов. Если кардинальные числа характеризуют класс эквивалентности относительно взаимно-однозначного соответствия, то порядковое число возникает как характеристика класса эквивалентности над вполне упорядоченными множествами, относительно биективных соответствий, сохраняющих отношение полного порядка. Для конечных множеств ординал и кардинал совпадают, но для бесконечных множеств это не всегда так, все множества одного порядкового числа равномощны, но обратное, в общем случае, неверно. Конструируются ординалы таким образом, чтобы последовательно продолжить натуральный ряд за пределы бесконечности[15]:
,
,
- …
,
после чего, рассмотрев множество всех конечных порядковых чисел как 
,
,
- …
,
,
- …
Далее строится 


.
Доказано, что множество всех счётных ординалов (всех 



Бесконечномерные пространства[править | править код]
|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 декабря 2016) |
Фрактальная геометрия[править | править код]
|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 декабря 2016) |
В программировании[править | править код]
Машинная бесконечность — конструкция для представления бесконечных числовых значений в языках и системах программирования и операций с ними. Стандартная арифметика с плавающей запятой (IEEE 754-2008) содержит особые значения для +∞ и −∞ : порядок состоит из одних единиц (11…11), мантисса из одних нулей (00…00). Положительная бесконечность больше любого конечного числа, отрицательная — меньше любого. Операции с бесконечностью определяются особо: (+∞) + x = +∞, +∞ + (+∞) = +∞, +∞ − ∞ = NaN, log (+∞) = +∞, sin (+∞) = NaN и так далее.
Ряд языков программирования позволяет работать с потенциально бесконечными структурами данных; например, в языке Haskell можно объявить бесконечный список и манипулировать им:
nat = [0..] -- список всех натуральных чисел even = map (*2) nat -- список всех чётных натуральных чисел fstevens = take 10 even -- первые десять чётных чисел
, при этом в среде выполнения будут вычисляться только те элементы бесконечной структуры, для которых запрошен непосредственный вывод (с использованием стратегии ленивых вычислений и применением рекурсии).
Особым проявлением бесконечности в программировании в смысле потенциальной вечности процесса выполнения является бесконечный цикл: техника их применения используется как сознательно (для возможности прерывания программы только внешним воздействием), так и возникает как ошибка (отсутствие или невыполнимость условия выхода из цикла: «программа зациклилась»).
В логике[править | править код]
Апории Зенона[править | править код]
Апории Зенона — серия апорий, относимых к Зенону Элейскому (вторая половина V века до н. э.) и дошедших в основном в изложении Аристотеля, будучи одними из первых примеров логических сложностей в оперировании с бесконечными объектами (хотя, прежде всего, с проблемами дискретного и непрерывного). Сформулированы апории таким образом, что многие из них являются предметом дискуссий и интерпретаций в течение всего времени существования логики, включая современность[16] и считаются первой постановкой проблемы использования бесконечности в научном контексте[17]. В апории «Ахиллес и черепаха» демонстрируется трудность суммирования убывающих бесконечно малых величин, притом эта антиномия не так проста, как иногда интерпретируется: как отмечают Гильберт и Бернайс в «Основаниях математики», для разрешения парадокса необходимо актуализировать бесконечную последовательность событий таким образом, чтобы принять её всё-таки завершаемой[18]. «Дихотомия», хотя может быть разрешена представлением о пределе сходящейся последовательности 
Парадоксы теории множеств[править | править код]
|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 декабря 2016) |
В философии[править | править код]
Древнеиндийская философия[править | править код]
В «Иша-упанишаде», относимой к IV—III веках до нашей эры обнаруживается представление о том, что добавление или удаление части из бесконечного объекта оставляет его бесконечным[20]. В джайнистском трактате Сурья-праджнапти-сутра (англ. Sūryaprajñapti), относимом к 400-м годам до н. э., все величины разделены на три категории и три подкатегории — перечислимые (малые, средние и большие), неперечислимые («почти неперечислимые», «истинно неперечислимые» и «неперечислимо неперечислимые») и бесконечные («почти бесконечные», «истинно бесконечные» и «бесконечно бесконечные»)[21], это разделение было по-видимому первой попыткой не просто различить виды бесконечного, но и измерить соотношение между ними, а идея выделять подкатегории бесконечных величин и упорядочивать их близка к концепции трансфинитных чисел Кантора.
Древнегреческая философия[править | править код]
У древнегреческих философов бесконечное обычно фигурирует как нечто неоформленное, несовершенное, близкое к хаосу или даже с ним отождествляемое[22], так, в пифагорейском списке противоположностей бесконечность отнесена к стороне зла. Среди древнегреческих философов, позитивно использующих категорию бесконечного выделяются Анаксимандр, вводящий космологическое начало как бесконечное вместилище — апейрон (греч. ἄπειρον), и атомисты (Демокрит, Левкипп), согласно которым существует бесконечное число миров, образованных из бесконечного числа атомов, содержащихся в бесконечном пустом пространстве[23]. При этом атомистская концепция оппонировала континуалистскому подходу, в котором пространство и время считались бесконечно делимыми, тогда как у атомистов постулировались первичные неделимые элементы, а апории Зенона[⇨] были призваны показать логическую несостоятельность обоих подходов[24].
Но господствующим мнением в древнегреческой философии было отрицание актуальной бесконечности, наиболее характерное отражение этих воззрений представлено у Аристотеля в «Физике», где он отказывает в бесконечности космосу, бесконечности последовательности причин, говоря о возможности бесконечного прироста натурального ряда и бесконечности деления отрезка на малые составляющие только как о потенциальной бесконечности[⇨]. Аристотелю же принадлежит классификация бесконечности на экстенсивную — возникающую при неограниченном добавлении предметов в совокупность, и интенсивную — появляющуюся при неограниченном углублении в строение объекта[25]
На позициях отрицания актуальной бесконечности и оперирования только с потенциальной бесконечностью стоят и античные геометры, в частности, у Евклида в «Началах» второй постулат утверждает возможность произвольно долго продолжать прямую, но сами прямые и плоскости рассматриваются как конечные, хоть и почти неограниченно «большие»[1].
В работах неоплатоников, прежде всего, у Плотина, в связи с проникновением представлений восточной мистики и во многом под влиянием работ Филона Александрийского, давшего эллинистическую интерпретацию христианского Бога, формируется представление об актуальной бесконечности Ума как бесконечно могущественного и единого, и потенциальной бесконечности безграничной материи[26].
Европейская средневековая философия[править | править код]
В раннехристианской и раннесредневековой философии (Ориген, Августин, Альберт Великий, Фома Аквинский) унаследовано от Аристотеля отрицание актуальной бесконечности в мире, при признании в том или ином виде за христианским Богом актуально бесконечного[1].
В трудах схоластов XIII—XIV веков (Уильяма из Шервуда, Хейтсбери, Григория из Римини) явно обозначается различие между понятиями потенциальной и актуальной бесконечности (в ранних сочинениях потенциальную и актуальную бесконечность называют синкатегорематической и категорематической бесконечностями соответственно), но сохраняется отношение к актуально бесконечному как божественному[1], либо постулируется полное отрицание актуальной бесконечности (лат. infinitum actu non datur). Однако уже Оккам обращает внимание на возможность признания существования континуума и его частей как актуально существующих при сохранении за ними свойств бесконечного — возможности бесконечного деления на составляющие части[27], а Суайнсхед в подтверждение своим рассуждениям о бесконечной делимости континуума математически доказывает утверждение о сумме бесконечного числового ряда[⇨][28]. Орем, развивая построения Суайнсхеда, выстраивает систему геометрических доказательств сходимости бесконечных рядов, строит пример плоской фигуры, бесконечной по протяжённости, но с конечной площадью[7].
В XV веке Николай Кузанский создаёт учение об «абсолютном максимуме», который он считает бесконечной мерой всех конечных вещей, тем самым давая представление, совершенно не совпадающее с античным: всё конечное рассматривается как ограничение актуально существующей божественной бесконечности (лат. possest), в противоположность господствовавшему представлению о существовании конечных вещей и потенциальности бесконечного[29].
Философия Нового времени[править | править код]
Представления Николая Кузанского развиты у Спинозы, согласно которому вещи получают своё бытие внутри бесконечной божественной субстанции посредством самоопределения через отрицание[30]. От этих представлений идёт и признание в XVI—XVII веках идеи о бесконечности Вселенной, которые утвердились благодаря гелиоцентрической системе Коперника, просветительской работе Бруно, исследованиям Кеплера и Галилея[31][1]. Кеплер и Галилей начинают использовать методы бесконечного в математической практике, так, Кеплер, опираясь на идеи Николая Кузанского, аппроксимирует окружность правильным многоугольником со стремящимся к бесконечности числом сторон[32], а Галилей, обращая внимание на соответствии между числами и их квадратами, отмечает невозможность применения тезиса «целое больше части» к бесконечным объектам[6].
Значительная роль в представлении о природе непрерывного и сущности континуума привнесена учеником Галилея Кавальери, который в трактате «Геометрия, изложенная новым способом при помощи неделимых непрерывного» (1635) рассматривал плоские фигуры как бесконечные множества заполняющих их отрезков, а объёмные тела — как состоящие из бесконечного числа параллельных плоских фигур, используя такие метафоры: линия состоит из точек также, как и ожерелье из жемчужин, плоская фигура из линий, также как и ткань из нитей, тело из плоскостей — как книга из страниц; с использованием этого «метода неделимых» Кавальери получил значительные математические результаты[33].
Декарт невозможность познания Бога из бытия сотворённого им мира аргументирует несоизмеримостью конечного и актуально бесконечного, непостижимость которого, по его представлению, заключена уже в самом формальном определении бесконечности[34]. Соответственно, подлинно бесконечным Декарт признаёт лишь всемогущего Бога, а такие проявления бесконечности, как «бесконечность человеческой воли», считает проявлениями божественного образа в существе человека[1].
Наиболее последовательным сторонником существования актуальной бесконечности был Лейбниц, в «Монадологии» он последовательно проводит идею бесконечности монад в универсуме, в каждой его части, выраженной в форме материи, обуславливая устойчивость этих частей законом предопределённой гармонии и особыми принципами подчинения монад, при этом рассматривая и монады, в свою очередь, как бесконечный в пространстве и времени универсум[1]. Эти представления Лейбница нашли отражение в его фундаментальных трудах по исчислению бесконечно малых, представляя инфинитезимали как монады[⇨]. Созданное Ньютоном и Лейбницем дифференциальное исчисление, явно актуализировавшее инфинитезимали, вызвало широкую и длительную дискуссию среди философов XVII—XVIII веков, наиболее последовательным противником методов, использующих бесконечно малые величины, был Беркли, эти дискуссии получили отражение в культуре в фабулах «Путешествий Гулливера» Свифта и «Микромегаса» Вольтера[35].
Кант в «Критике чистого разума» отказывает в возможности рассмотрения как бесконечных чисел, так и бесконечных величин; на основе анализа антиномий чистого разума Кант характеризует мир ни как конечный, ни как бесконечный, а как «неопределённый»[1].
Гегель развивает идею теснейшей связи, почти тождества, бесконечного и абсолютного[36], особо рассматривает «дурную бесконечность» как отрицание конечного и как диалектическое преодоление антагонизма вводит «истинную бесконечность»; истинно бесконечен по Гегелю только Абсолютный дух[1]. В философии диалектического материализма подчёркивается представление о бесконечном, как о диалектическом процессе[37][38], само понятие бесконечного в ней имеет различные смыслы: простейшая, практическая бесконечность; бесконечность, как абсолютность, всеобщность, завершённость; бесконечность интеллектуального мира; реальная бесконечность. Бесконечность пространства и времени Энгельс рассматривает как пример «дурной бесконечности».
Наиболее значительным трудом XIX века о бесконечности, в большей степени философским[39], чем математическим стала монография Больцано «Парадоксы бесконечного»[en] (опубликована в 1851 году, уже после смерти автора)[1], в ней систематически изучаются бесконечные множества чисел, приводятся логические и математические доводы в пользу рассмотрения актуальной бесконечности и предлагается инструментарий для исследования родов бесконечности с использованием понятия взаимно-однозначного соответствия[39].
На идейной основе работы Больцано и создана в конце XIX века в трудах Кантора со значительным участием Дедекинда теория множеств[⇨] (сам термин «множество» — нем. menge, в качестве обозначения актуально бесконечного объекта впервые использован у Больцано), именно в теории множеств впервые мотивированно рассмотрено соотношение разных видов бесконечного, в частности, средствами понятия о мощности установлено соотношение между количеством элементов натурального ряда (счётного множества, 

Современная философия[править | править код]
В философии XX века основное содержание исследований вопросов, связанных с бесконечностью, тесно стыкуется с основаниями математики, и прежде всего, проблемами теории множеств[43].
Рассел, в системе которую он построил совместно с Уайтхедом в Principia Mathematica в преодоление парадоксов теории множеств[⇨], постулировал существование бесконечности посредством введения аксиомы бесконечности, притом в ней не допускается в возможности выведения бесконечности из других априорных понятий, не считается выводимым понятие бесконечности сугубо аналитически из принципа недопущения противоречий. Также Рассел не считал возможным изыскать апостериорное обоснование бесконечности, основываясь на здравом смысле и опыте, особо отмечая, что нет никаких оснований веры в бесконечность пространства, бесконечность времени или бесконечную делимость предметов. Таким образом, бесконечность по Расселу — гипотетический императив, которым в разных системах можно пользоваться или нет, но который невозможно обосновать или опровергнуть[44].
Реализуя программу по преодолению парадоксов теории множеств, Гильберт и Бернайс сформировали принципы, идентифицируемые как «гильбертов финитизм», согласно которым утверждения о свойствах, сформулированных для всех элементов бесконечной совокупности возможны только при условии их воспроизводимости для каждого конкретного элемента, при этом, не ограничивая возможные абстракции бесконечного, в том числе, и трансфинитную индукцию. Витгенштейн, наиболее радикально развивший концепцию финитизма в аналитической философии, считал возможным рассматривать бесконечное только как запись рекурсивного процесса и принципиально отвергал возможность рассмотрения разных классов бесконечности[45].
В школах, исходящих из неокантианства и феноменологии также исследовались вопросы бесконечного, так, Кассирер в дискуссии с Хайдеггером («Давосская дискуссия», 1929) вводит имманентную бесконечность, возникающую как объективизация сферы переживаний[46], в 1950-е — 1960-е годы программные работы, посвящённые бесконечному, написаны Койре и Левинасом[47].
Индукция[править | править код]
Индукция — классический логический метод, позволяющий перейти от частных утверждений ко всеобщим, в том числе, относительно бесконечного множества объектов. Индукция относительно натурального ряда без какой-либо формализации отмечается ещё у Прокла и Евклида, тогда как осознание её как метода математической индукции относят к Паскалю и Герсониду[48]. В современных обозначениях математическая индукция заключается в силлогизме:
,
то есть, выводе свойства 
Метод математической индукции считается надёжным, но распространить его можно только на счётные вполне упорядоченные множества. Попыткой распространить индукцию на произвольные вполне упорядоченные множества было создание метода трансфинитной индукции Кантором в рамках теории множеств[⇨], использующего идею трансфинитных (порядковых) чисел.
В интуиционистской логике для применения индуктивного рассуждения на несчётные совокупности (описываемые в интуиционизме как потоки) применяется бар-индукция[en][49].
Символы[править | править код]
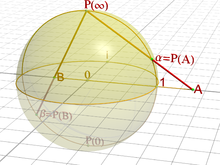
Уроборос на могиле как символ вечности, возможный прототип символа бесконечности «∞»
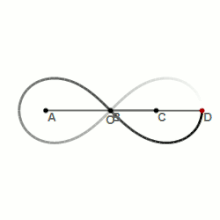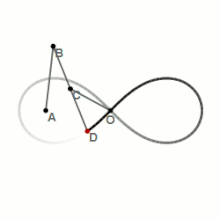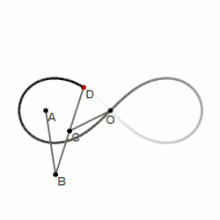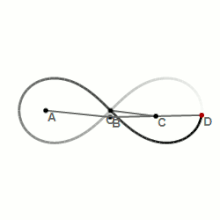
Лемниската Бернулли — алгебраическая кривая, похожая на символ бесконечности, впервые описана в 1694 году, спустя почти полвека после появления символа «∞» у Валлиса
Символ бесконечности 
Символы бесконечности, используемые для кардинальных чисел — 
Примечания[править | править код]
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 НФЭ, 2010.
- ↑ Бесконечность в философии / И. С. Алексеев // Бари — Браслет. — М. : Советская энциклопедия, 1970. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 3).
- ↑ Катасонов В. Н. Непрерывность и прерывистость // Новая философская энциклопедия. — 2-е изд., испр. и дополн.. — М.: Мысль, 2010. — Т. 2. — 2816 с. — 5000 экз. — ISBN 978-5-244-01115-9.
- ↑ 1 2 Гордон, Кусраев, Кутателадзе, 2011, с. 10—13.
- ↑ Книга IX, утверждение 20
- ↑ 1 2 Бурбаки, 1963, с. 39.
- ↑ 1 2 3 4 5 Паплаускас А. Б. Доньютоновский период развития бесконечных рядов. I // Юшкевич А. П. (отв. редактор) Историко-математические исследования. — М.: Наука, 1973. — Т. XVIII. — С. 104—131.
- ↑ Dani S. G. Ancient Indian Mathematics – A Conspectus // Resonance. — 2012. — Т. 17, № 3. — С. 236—246.
- ↑ Паплаускас А. Б. Доньютоновский период развития бесконечных рядов. II. Пьетро Менголи // Юшкевич А. П. (отв. редактор) Историко-математические исследования. — М.: Наука, 1974. — Т. XIX. — С. 143—157.
- ↑ Паплаускас А. Б. Доньютоновский период развития бесконечных рядов. III // Юшкевич А. П. (отв. редактор) Историко-математические исследования. — М.: Наука, 1975. — Т. XX. — С. 257—281.
- ↑ Гордон, Кусраев, Кутателадзе, 2011, с. 26.
- ↑ Кудрявцев Л. Д. Краткий курс математического анализа. — 3-е изд. перераб.. — М.: Физматлит, 2005. — Т. 1. — С. 19. — 400 с. — ISBN 5-9221-0184-6.
- ↑ Бесконечность — статья из Математической энциклопедии. Драгалин А. Г. С помощью Н. а. был обнаружен ряд новых фактов. Многие классич. доказательства заметно выигрывают в наглядности при изложении их методами нестандартного анализа
- ↑ Иногда для бесконечных кардинальных чисел, представляющих мощность последовательного взятия булеанов от счётного множества используют бет-нотацию (от второй буквы еврейского алфавита — бет), в этих обозначениях обобщённая континуум-гипотеза формулируется как
- ↑ Такую схему определения предложил фон Нейман в 1920-е годы, Кантор изначально использовал другой способ
- ↑ Яновская С. А. Преодолены ли в современной науке трудности, известные под названием «апории Зенона»? // Проблемы логики / Таванец П. В.. — М., 1963. — С. 116—136.
- ↑ Гайденко П. П. Эволюция понятия науки (становление и развитие первых научных программ). Элейская школа и первая постановка проблемы бесконечности. — М.: Наука, 1980. Архивная копия от 25 октября 2011 на Wayback Machine
- ↑ Гильберт Д., Бернайс П. Основания математики. — М.: Наука, 1979. — Т. 1. Логические исчисления и формализация арифметики. — С. 40. — 558 с.
- ↑ Даан-Дальмедико, Пейффер, 1986, с. 236—238.
- ↑ серб. पूर्णमदः पूर्णमिदं पूर्णात् पूर्णमुदच्यते पूर्णस्य पूर्णमादाय पूर्णमेवावशिष्यते — «Полное То, полное это. От полного полное берётся. Полным полное прибывает, полное лишь остаётся», перевод Сыркина
- ↑ Joseph, G. G. The Crest of the Peacock. Non-European Roots of Mathematics. — 3rd. — Princeton: Princeton University Press, 2011. — P. 349—355. — 562 p. — ISBN 978-0-691-13526-7.
- ↑ НФЭ, 2010, Античная мысль в основном рассматривает бесконечное как неоформленное, как не ставшее и, следовательно, несовершенное <…> Бытие в античной мысли связано с категорией меры и предела. Бесконечное выступает как беспредельное, безграничное, почти не существующее – μὴὄν и потому есть нечто близкое к хаосу, а иногда и отождествляется с ним.
- ↑ НФЭ, 2010, …в античной философии были мыслители, которые более позитивно используют категорию бесконечного. Прежде всего к ним относится Анаксимандр, у которого главным началом космологии служит апейрон<…> кроме того, здесь нужно назвать атомистов Левкиппа и Демокрита, у которых бесконечное пустое пространство содержит бесконечное количество атомов, образующих бесконечное количество миров.
- ↑ Даан-Дальмедико, Пейффер, 1986, с. 236.
- ↑ Виленкин, 1983, с. 14—15.
- ↑ НФЭ, 2010, Ум Плотин уже называет бесконечным в следующих смыслах: в смысле его бесконечного могущества, его единства и его самодостаточности. Все сущее оказывается тем самым между двумя бесконечностями: актуальной бесконечностью Ума и потенциальной бесконечностью мэональной материи, лишённой границ и формы и получающей свои определения только через «отражения» совершенств высшего бытия.
- ↑ лат. Sed omne continuum est actualiter existens. Igitur quaelibet pars sua est vere existens in rerum natura. Sed partes continui sunt infinitae quia non tot quin plures, igitur partes infinitae sunt actualiter existentes — «Но всякий континуум актуально существует. Следовательно, и его части существуют в природе. Но части континуума бесконечны, потому что нельзя сказать сколь их много, и, стало быть, бесконечные части актуально существуют»
- ↑ Боголюбов А. Н. Математики. Механики. Биографический справочник. — Киев: Наукова думка, 1983. — 639 с.
- ↑ НФЭ, 2010, … для Кузанца, наоборот, любая конечная вещь выступает как потенциальное ограничение актуально бесконечной божественной возможности — бытия (possest).
- ↑ НФЭ, 2010, … Аналогично и в рамках пантеизма Спинозы оказывается, что omnis determinatio est negatio (каждое определение есть отрицание): не через предел, не через ограничение бесформенной материи получают вещи своё бытие, а именно от подлежащей бесконечной божественной субстанции, внутри которой самоопределение выступает как частичная негация.
- ↑ Даан-Дальмедико, Пейффер, 1986, с. 43—44.
- ↑ Даан-Дальмедико, Пейффер, 1986, с. 43—45.
- ↑ Даан-Дальмедико, Пейффер, 1986, с. 249.
- ↑ Гарнцев М. А. Проблема абсолютной свободы у Декарта // Логос. — 1996. — № 8. Архивировано 24 ноября 2015 года.
- ↑ Гордон, Кусраев, Кутателадзе, 2011, с. 13—14.
- ↑ «Бесконечное в его простом понятии можно, прежде всего, рассматривать как новую дефиницию абсолютного…» Гегель Г. В. Ф.Наука логики. // Соч., т. V. — М.: Госиздат, 1927. — С. 136.
- ↑ «Говоря о бесконечно большом и бесконечно малом, математика вводит такое качественное различие, которое имеет даже характер непреодолимой качественной противоположности…» Маркс К., Энгельс Ф. Диалектика природы // Соч., т. 20. — М.: Политиздат, 1956. — С. 574.
- ↑ «Бесконечность есть противоречие, и она полна противоречий… Именно потому, что бесконечность есть противоречие, она представляет собой бесконечный, без конца развертывающийся во времени и пространстве процесс. Уничтожение этого противоречия было бы концом бесконечности.» Маркс К., Энгельс Ф. Анти-Дюринг // Соч., т. 20. — М.: Политиздат, 1956. — С. 51.
- ↑ 1 2 Бурбаки, 1963, с. 39—40.
- ↑ НФЭ, 2010, Создатель теории множеств Кантор пытался дать и богословское применение своим конструкциям с актуальной бесконечностью (Кантор вообще считал теорию множеств относящейся столько же к метафизике, сколько и к математике). Он различал три типа бесконечного: бесконечное в Боге («в уме Бога») – Абсолютное, в тварном мире – Трансфинитное, в уме человека – трансфинитные числа (ординалы).
- ↑ Dedekind, R. Was sind und was sollen die Zahlen?. — Braunschweig: Drud und Berlag von Friedrich Bieweg, 1893. — 60 с. Архивная копия от 13 мая 2013 на Wayback Machine
- ↑ 1 2 Ф. А. Медведев. Развитие теории множеств в XIX веке. — М.: Наука, 1965. — С. 133—137, 144—157. — 232 с. — 2500 экз.
- ↑ НФЭ, 2010, В 20 в. философские дискуссии вокруг проблем бесконечности соотносятся с теорией множеств и проблемой оснований математики.
- ↑ Суровцев В. А. Б. Рассел о бесконечности // Вестник Томского государственного университета. Философия. Социология. Политология. — 2010. — Т. 12, № 4. — С. 135—145. Архивировано 3 декабря 2015 года.
- ↑ Rodych, V. Wittgenstein’s Philosophy of Mathematics (англ.). The Stanford Encyclopedia of Philosophy. Stanford University Press (21 сентября 2011). Дата обращения: 25 мая 2013. Архивировано 25 мая 2013 года.
- ↑ Вейнмейстер А. В. Давосская дискуссия между Кассирером и Хайдеггером // Вестник Оренбургского государственного университета. — 2007. — № 2. Архивировано 6 июня 2015 года.
- ↑ Ямпольская А. В. Идея бесконечного у Левинаса и Койре // Вопросы философии. — 2009. — № № 8. — С. 125—134. Архивировано 10 октября 2013 года.
- ↑ Nachum L. Rabinovih. Rabbi Levi ben Gershom and the origins of mathematical induction // Archive for History of Exact Sciences. — 1970. — Вып. 6. — С. 237—248.
- ↑ Бесконечность — статья из Математической энциклопедии. Драгалин А. Г.
- ↑ De sectionibus conicis Архивная копия от 2 января 2014 на Wayback Machine
- ↑ Scott, Joseph Frederick (1981), The mathematical work of John Wallis, D.D., F.R.S., (1616-1703) (2 ed.), AMS Bookstore, с. 24, ISBN 0-828-40314-7, <https://books.google.com/books?id=XX9PKytw8g8C> Архивная копия от 25 сентября 2014 на Wayback Machine, Chapter 1, page 24 Архивная копия от 18 ноября 2016 на Wayback Machine
- ↑ Martin-Löf, Per & Mints, G. E. (1990), COLOG-88: International Conference on Computer Logic Tallinn, USSR, December 12–16, 1988: proceedings, Springer, с. 147, ISBN 3-540-52335-9, <https://books.google.com/books?id=nfnGohZvXDQC> Архивная копия от 1 октября 2014 на Wayback Machine, page 147 Архивная копия от 2 октября 2014 на Wayback Machine
- ↑ Robertson, Robin; Combs, Allan. The Uroboros // Indra’s Net: Alchemy and Chaos Theory as Models for Transformation. — Quest Books, 2009. — ISBN 978-0-8356-0862-6
- ↑ Даубен Дж. Георг Кантор и рождение теории трансфинитных множеств. Scientific American, издание на русском языке, № 8 (август), с. 76–86 (1 июля 1983). Дата обращения: 5 мая 2013. Архивировано 10 мая 2013 года.
Литература[править | править код]
- Н. Бурбаки. Основания математики. Логика. Теория множеств // Очерки по истории математики / И. Г. Башмакова (перевод с французского). — М.: Издательство иностранной литературы, 1963. — С. 37—53. — 292 с. — (Элементы математики).
- Виленкин Н. Я. В поисках бесконечности. — М.: Наука, 1983.
- Гордон Е. И., Кусраев А. Г., Кутателадзе С. С. Инфинитезимальный анализ: избранные темы. — М.: Наука, 2011. — 398 с. — ISBN 978-5-02-036137-9.
- Грасиан, Энрике. Открытие без границ. Бесконечность в математике. — М.: Де Агостини, 2014. — 144 с. — (Мир математики: в 45 томах, том 18). — ISBN 978-5-9774-0713-7.
- Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики = Routes et dédales / Перевод с французского А. А. Брядинской под редакцией И. Г. Башмаковой. — М.: Мир, 1986. — С. 394—402. — 432 с. — (Современная математика. Популярная серия). — 50 000 экз.
- Бесконечность / Катасонов В. Н. // «Банкетная кампания» 1904 — Большой Иргиз. — М. : Большая российская энциклопедия, 2005. — С. 413—415. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 3). — ISBN 5-85270-331-1.
- Катасонов В. Н. Бесконечное // Новая философская энциклопедия / Ин-т философии РАН; Нац. обществ.-науч. фонд; Предс. научно-ред. совета В. С. Стёпин, заместители предс.: А. А. Гусейнов, Г. Ю. Семигин, уч. секр. А. П. Огурцов. — 2-е изд., испр. и допол. — М.: Мысль, 2010. — ISBN 978-5-244-01115-9.
- Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — 446 с.
Что такое бесконечность?
В математике бесконечность — это понятие, которое описывает отсутствие границы или ограничений. Оно используется для описания неограниченных числовых множеств, функций и других математических объектов.
Интересные факты о знаке бесконечности
- Знаете ли вы, как называется знак бесконечности (∞) ? Его название — лемниската. Это название происходит от греческого слова “lemniskos”, что означает “ленточка”.
- Знак бесконечности используется в различных областях математики, таких как теория множеств, математический анализ, теория вероятностей, геометрия и другие.
- В математике существуют различные типы бесконечностей. Например, есть бесконечность, которая описывает неограниченное возрастание функции, и бесконечность, которая описывает расширение числового множества до бесконечности.
- Бесконечность может быть как положительной, так и отрицательной. Например, при делении числа на очень большое число, результат может стремиться к нулю, что описывается как бесконечно малое число.
- В некоторых культурах знак бесконечности используется как символ бесконечности, непрерывности и вечности. Он может быть изображен как петля, восьмерка или знак бесконечности в математической нотации.
Бесконечность обычно рассматривается как число, поскольку оно используется для обозначения чисел вещей, но это не реальное число. Если система счисления включает бесконечно малые числа, то это записывается как (frac{1}{ ∞}), чем больше число в знаменателе, тем меньше число в целом.
В конце (19) века до начала (20) века, Георг Кантор сделал много мыслей о бесконечности или бесконечных множеств. Он разработал теорию, утверждающую, что существуют бесконечные множества разных размеров.
Часто задаваемые вопросы:
✅ Что такое бесконечность в математике?
↪ Бесконечность – это понятие, которое описывает отсутствие границы или ограничений. Оно используется для описания неограниченных числовых множеств, функций и других математических объектов.
✅ Какие типы бесконечностей существуют в математике?
↪ В математике существует несколько типов бесконечностей, таких как бесконечность, описывающая неограниченное возрастание функции, бесконечность, описывающая расширение числового множества до бесконечности, бесконечно малые числа, описывающие приближение к нулю.
✅ Где используется понятие бесконечности в математике?
↪ Бесконечность используется в различных областях математики, таких как теория множеств, математический анализ, теория вероятностей, геометрия и другие.
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Развитие
понятия «бесконечность» в математике
Термин бесконечность соответствует
нескольким различным понятиям, в зависимости от области применения, будь то
математика, физика, философия или повседневная жизнь
Бесконечность чужда нашему
непосредственному опыту, и в большинстве культур появилась как абстрактное
количественное обозначение чего-то непостижимо большого, в применении к
сущностям без пространственных границ.
Одним из
самых выдающихся философов Древней Греции, задумывавшимся над проблемой
конечного и бесконечного, был Пифагор. «Число – олицетворение добра, а
бесконечная пустота – олицетворение зла. Конечное и упорядоченное неизмеримо
ценнее, чем бесконечное и неопределенное. В конечности – красота и
совершенство. В безграничности – незавершенность и несовершенство. Следует
преклоняться перед конечным и питать отвращение к бесконечному», – в этом
выражалось учение Пифагора о бесконечности.
Еще один
древнегреческий ученый, Аристотель, понимал, что наука о природе не может отказаться
от понятия бесконечного. По его мнению, бесконечность – это процесс, состоящий
из последовательных шагов, где за каждым очередным шагом имеется следующий и
нет последнего.
Например: бесконечная
последовательность натуральных чисел, которую можно получить путем
последовательного прибавления единицы. Подобную бесконечность Аристотель
называл потенциальной, которую он понимал, как осуществимость сколь угодно
большого, но конечного числа объектов. Бесконечность же, которая предполагает
возможность завершения бесконечного процесса, он называл актуальной. Аристотель
утверждал, что математики вполне могут обойтись потенциальной бесконечностью.
Актуальную бесконечность следует отбросить как ненужную. Величайший мыслитель
Древней Греции, Аристотель достиг высот теоретической мысли, но в то же время
провел непроходимую грань между прикладными задачами и научной теорией. Он
утверждал, что математика должна заниматься только чисто теоретическими
операциями, а реальные вещи ее совершенно не должны интересовать.
Первым среди
древнегреческих ученых, кто применил теоретические знания, в частности понятие
бесконечности для решения практических задач, был Архимед. Он первым вычислил
площадь круга как предел площади, вписанного в окружность правильного
многоугольника, когда число его сторон ограниченно возрастает, то есть
стремится к бесконечности.
Определение бесконечности в словарях
встречаются разные, вот некоторые из них.
1. Отсутствие конца, предела наличию каких–либо
однородных объектов в пространстве или момента осуществления каких-либо
процессов.
2. Пространство, не имеющее видимых границ,
пределов.
3. Условная величина, которая больше любого
наперёд заданного значения (Обозначается знаком ∞ ).
Свойства бесконечности
1. Между двумя последовательными целыми числами
не существует никаких других целых чисел
2. Множество Целых чисел
называется Дискретным
3. Между любыми двумя рациональными числами
всегда будет располагаться бесконечно много других рациональных чисел
4. Множество Рациональных чисел
называется Непрерывным
5. Если мы можем указать
следующее число в множестве, то оно имеет Плотность
6. Плотность делает бессмысленным понятие «следующего» рационального числа
ЗАКЛЮЧЕНИЕ
В заключении своей исследовательской
работы хотелось бы сказать, что роль бесконечности в математике очень велика.
Она способна удивить, ведь, работая только с конечными промежутками, мы
никогда бы не задумались о том, что в множестве натуральных чисел и в множестве
натуральных чётных неотрицательных чисел одинаковое количество элементов, ведь
множество натуральных чётных неотрицательных чисел – это часть множества
натуральных чисел, и, по идее, оно должно иметь меньше элементов. Я считаю, что
это удивительно.
Конечно же, понятие бесконечности как
в математике, так и в других науках неоднозначно, и человечеству только
предстоит узнать всё о ней. До сих пор не известно бесконечна ли галактика,
вселенная и т.д.
Математика —
это шаг через бесконечность. Освоение математики — это, когда вы
становитесь с бесконечностью «на ты». И чем больше вы
«на ты» с бесконечностью, тем лучше вы понимаете математику. Это
наука о бесконечности. В этом смысле, математика и религия
дополняют друг друга. Религия — это знание о бесконечности,
математика — наука о бесконечности. Это две ипостаси бытия.
Вы когда-нибудь были на детской площадке, играя в игру, называя самое большое число, которое вы можете придумать? Как быстро кто-то говорит «бесконечность»? Затем следующий человек говорит «бесконечность плюс один», и кажется, что игра никогда не закончится. Но действительно ли бесконечность плюс один больше бесконечности? Можем ли мы заниматься математикой с бесконечностью?
Георг Кантор (1845–1918) был одним из первых математиков, изучавших бесконечность. Он придумал различные примеры появления бесконечности в математике. Он также обнаружил, что существуют разные типы бесконечности. Это заставило других математиков отвергнуть его работу как некорректную и запутанную. Именно Дэвид Гильберт сделал бесконечность понятной в 1924 году. Его объяснение было историей об отеле, в котором, даже когда он был заполнен, было место для большего количества гостей. Эта статья пытается объяснить бесконечность аналогичным образом.
Бесконечность — штука странная и сбивающая с толку математиков. Чтобы помочь нам понять странное поведение бесконечности, математики вернулись к основам и попытались определить, что значит считать.
Представьте, что у вас есть сумка, полная сладостей. Вы не видите содержимое сумки, но хотите знать, сколько у вас сладостей. Лучший способ сделать это — достать из пакета первую конфету и сказать «один». Затем вы достаете вторую конфету и говорите «два». Вы бы продолжали делать это, пока сумка не опустеет. Последнее число, которое вы скажете, — это сколько сладостей у вас в сумке. Так мы учимся считать, независимо от того, какие предметы у вас в сумке.
Мощность множества, кардинальное число множества — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.
Мощность предметов в сумке — количество предметов в сумке. Например, мешок с тремя конфетами имеет мощность три. Сумка с одной конфеткой, одним роботом и карандашом также имеет мощность три. Неважно, что это за предметы, имеет значение только количество. В сумке могут быть более абстрактные объекты, например сумка с номерами 1, 2 и 3.
В двух сумках с одинаковой мощностью находится одинаковое количество предметов. Мы можем объединить объекты в обе сумки, и ни в одной из них ничего не останется. Это дает нам еще один способ подсчета объектов. Если нам известна мощность одного мешка, но неизвестна мощность другого, мы можем проверить, можем ли мы объединить объекты в пары в обоих мешках.
Например, у вас есть пакет конфет, но вы не знаете, сколько конфет в нем. На этот раз у вас тоже восемь друзей. Если вы можете дать каждому из восьми друзей ровно по одной сладости, не оставив сладостей, то мощность пакета со сладостями будет равна восьми. Если хотя бы один друг не получит конфету, то мощность мешка меньше восьми. Если хотя бы одна конфета осталась, то мощность пакета больше 8.
Счетное множество
Представьте себе сумку, содержащую все «Натуральные числа», мешок, содержащий все положительные числа, 1, 2, 3, 4 и так далее.
Мы используем символ ℕ для обозначения этого мешка . Какова мощность? Очевидно, что у него нет мощности 4, так как ℕ содержит как минимум пять объектов, а именно числа 1, 2, 3, 4 и 5. Та же логика работает для любого числа. Выберите любое число, скажем n , тогда мешок ℕ будет содержать не менее n + 1 объектов, а именно числа 1, 2, 3,…, n и n + 1. Это показывает, что мощность ℕ не является числом, и мы говорим, что ℕ счетно бесконечно.
Сумка, содержащая бесконечно много предметов, но мы все еще можем их подсчитать. Другими словами, мешок той же мощности, что и ℕ.
Мешок объектов счетно бесконечен, если он имеет ту же мощность, что и ℕ. Другими словами:
- В сумке бесконечно много предметов, поэтому мы всегда можем что-то из нее вытащить.
- Мы можем связать каждый объект в сумке с уникальным положительным целым числом (другими словами, мы можем подсчитать объекты).
Пример 1: четные числа
Представьте себе две сумки. Одна со всеми положительными числами называется ℕ, а другая со всеми положительными четными числами, который называется 2ℕ. Казалось бы, положительных чисел больше, чем положительных четных. Но мы покажем, что вы можете связать каждое четное число ровно с одним числом таким образом, чтобы не было остатков. Выходит, что и 2ℕ имеют одинаковую мощность.
Прежде чем мы это сделаем, нам нужен способ отличить числа, которые мы берем из сумки ℕ, и четные числа, которые мы берем из сумки 2ℕ. Мы добавляем «-е» в конец любого числа из пакета ℕ. Примеры:
- 6-е — число N, а 6 – четное число от 2ℕ.
- 7-е — это число от ℕ, а поскольку 7 не четное, его нет в нашей сумке 2ℕ.
Чтобы объединить числа из ℕ и 2ℕ в пару, нужно сказать: n- е число соединяется с четным числом 2 n . Примеры:
- Четвертое число сочетается с четным числом 8.
- Пятое число ставится в пару с четным числом 10.
- 57-е число связано с четным числом 114.
Мы видим, что каждое число из ℕ попадает в пару с четным числом. Также видим, что каждое четное число объединяется с числом, так как четное число n объединяется с ( n ÷ 2) -м числом. Это означает, что мы соединили каждое число в ℕ с числом в 2ℕ, и никаких остатков нет ( рис. 1 ). Следовательно, и 2ℕ имеют одинаковую мощность. Мешок с четными числами счетно бесконечен. Это означает, что положительных чисел столько же, сколько положительных четных.
Итак, чисел столько, сколько есть четных.
ДОБАВЛЕНИЕ ЕДИНИЦЫ К БЕСКОНЕЧНОСТИ
Пример 2: Представьте себе две сумки, каждая из которых содержит все положительные числа. Обе сумки в настоящее время содержат одинаковое количество объектов (они оба счетно бесконечны). Теперь добавьте один предмет, букву A, во вторую сумку. Во второй сумке больше предметов, чем в первой? Нет, на самом деле у них одинаковое количество предметов.
Как и раньше, мы называем первый мешок ℕ и добавляем «-е» в конец любого числа в этом мешке. Второй пакет, содержащий A, 1, 2, 3 и т. Д., Будет называться ℕ 0 . Мы объединяем каждый объект в с одним объектом в ℕ 0, используя два правила:
- 1-е число ставится в пару с буквой A из ℕ 0 .
- Когда n не равно единице, n- е число соединяется с числом n – 1 из ℕ 0 .
Примеры
- 1-е число ставится в пару с буквой А.
- 5-е число связано с числом 4.
- 30-е число связано с числом 29.
Таким образом, каждый объект в связан с одним объектом в ℕ 0 . Следовательно, обе сумки имеют одинаковую мощность, а значит одинаковое количество объектов.
Эта логика работает для любого количества вещей, которые мы добавляем в корзину ℕ. Итак, сколько бы конечных вещей мы ни добавили к ℕ, мешок по-прежнему счетно бесконечен и содержит такое же количество объектов.
ДОБАВЛЕНИЕ БЕСКОНЕЧНОСТИ К БЕСКОНЕЧНОСТИ
Пример 3 : Мы видели, что мешок, содержащий все положительные числа, счетно бесконечен. По той же логике мешок, содержащий все отрицательные числа, также счетно бесконечен. Что, если мы поместим в один пакет все положительные числа, все отрицательные числа и 0? Эта сумка больше, чем сумка ℕ?
Мы будем использовать символ Z, означает мешок, содержащий все числа (положительные, отрицательные и ноль) . Чтобы соединить числа в ℕ с числами Z, нам нужно использовать более сложные правила.
- Если n нечетное, то n- е число ставится в пару с числом ( n – 1) ÷ 2 в ℤ.
- Если n четно, то n- е число ставится в пару с числом– ( n ÷ 2) в ℤ.
Примеры:
- 4 четное и 4 ÷ 2 = 2. Итак, 4-е число ставится в пару с числом –2.
- 5 нечетно, поэтому мы делаем 5 – 1 = 4 и 4 ÷ 2 = 2. Итак, 5-е число объединяется с числом 2.
- 24-е число ставится в пару с числом –12.
- 57-е число ставится в пару с числом 28.
Опять же, мы соединили каждый объект в с объектом в ℤ ( рисунок 2 ). Это означает, что они имеют одинаковую мощность. Следовательно, счетно бесконечно. Чисел (положительных и отрицательных) столько же, сколько положительных.
Итак, чисел столько, сколько положительных и отрицательных.
ВЫЧИТАНИЕ ИЗ БЕСКОНЕЧНОСТИ
Мы определили, что добавление одного или бесконечного числа объектов в сумку, которая является счетно бесконечной, не увеличивает ее (см. Пример 3). Но что произойдет, если мы начнем удалять объекты из счетно бесконечного мешка?
Пример 4 : Представьте себе мешок, содержащий все положительные числа, и удалите из него цифру 1. Назовем эту сумку ℕ1 . Покажем, что мешок ℕ 1 счетно бесконечен, соединив каждый элемент из ℕ1 с элементом из ℕ. Как и раньше, мы будем добавлять «-е» в конец любого числа, идущего от ℕ.
Примеры
- 1-е число ставится в пару с номером 2.
- 5-е число связано с числом 6.
- 30-е число связано с числом 31.
Каждый объект N связан с одним объектом в ℕ 1 . Следовательно, обе сумки имеют одинаковую мощность, а значит, одинаковое количество объектов.
Эта логика работает для любого количества вещей, которые мы извлекаем из сумки ℕ. Независимо от того, сколько конечных вещей мы извлекаем из ℕ, мешок все равно счетно бесконечен и по-прежнему содержит такое же количество предметов.
А что если мы удалим счетное бесконечное количество объектов? Тогда ответ зависит от того, что мы удаляем.
Пример 5 : Мы знаем, что положительные четные числа счетно бесконечны (см. Пример 1). Представьте себе мешок, содержащий все положительные числа, и выньте из него все четные положительные числа. В сумке остались только положительные нечетные числа. Точно так же, как четные числа являются счетно бесконечными, нечетные числа также счетно бесконечны (чтобы увидеть это, мы объединяем n- е число в пару с нечетным числом 2 n – 1, см. Рисунок 3 ).
Итак, чисел столько, сколько нечетных.
В этом случае, начиная со счетно бесконечного мешка и удаляя из него счетное бесконечное количество объектов, мы все равно остаемся со счетным бесконечным числом объектов, или, другими словами, счетным бесконечным мешком.
Пример 6 : Представьте себе сумку со всеми положительными числами, например сумку ℕ. Представьте, что мы удалили все числа больше 1. Из ℕ мы удалили мешок N1 (см. Пример 4). У нас остается сумка с номером 1. Сумка, содержащая только номер 1, имеет мощность 1.
В этом случае, начиная со счетно бесконечного мешка и удаляя из него счетное бесконечное количество объектов, мы остаемся с единственным объектом.
ЗАКЛЮЧЕНИЕ
В этой статье показаны некоторые из странных проявлений бесконечности. Приведенные выше примеры показывают, что мы не можем работать с бесконечностью, как с числом. Когда мы выполняем сложение и вычитание, бесконечность ведет себя иначе, чем числа.
Хотя эта странность сначала сбивала с толку математиков, вернувшись к основам, им удалось понять бесконечность. Это повторялось на протяжении всей истории, что понятия, которые когда-то были загадочными, были наконец поняты, если тщательно подойти к определению.
Родители и педагоги, если вам понравилась статья, сохраняйте и делитесь ею с друзьями, оставляйте комментарии со своим мнением и конечно же ставьте «пальцы вверх», чтобы поддержать наш канал!
Наши математические кружки: https://matclass.ru/listok/
Наши задачники: https://matclass.ru/magazin
Зимние и летние каникулярные программы: https://matclass.ru/programma
Задачи настоящей статьи ограничиваются указанием на различные подходы к Б. в математике, освещаемые подробнее в других статьях.
1) Представление о бесконечно малых и бесконечно больших переменных величинах является одним из основных в математическом анализе. Предшествовавшая современному подходу к понятию бесконечно малой концепция, по которой конечные величины составлялись из бесконечно большого числа бесконечно малых «неделимых» (см. «Неделимых» метод), трактовавшихся не как переменные, а как постоянные и меньшие любой конечной величины, может служить одним из примеров незаконного отрыва бесконечного от конечного: реальный смысл имеет только разложение конечных величин на неограниченно возрастающее число неограниченно убывающих слагаемых.
2) Совсем в другой логической обстановке Б. появляется в математике в виде «несобственных» бесконечно удалённых геометрических образов (см. Бесконечно удалённые элементы). Здесь, например, бесконечно удалённая точка на прямой а рассматривается как особый постоянный объект, «присоединённый» к обычным конечным точкам. Однако неразрывная связь бесконечного с конечным обнаруживается и здесь, хотя бы при проектировании из центра, лежащего вне прямой, при котором бесконечно удалённой точке оказывается соответствующей прямая, проходящая через центр проектирования и параллельная основной прямой а.
Аналогичный характер имеет пополнение системы действительных чисел двумя «несобственными» числами +¥ и -¥, соответствующее многим запросам анализа и теории функций действительного переменного. Можно подойти с такой же точки зрения и к пополнению ряда натуральных чисел 1, 2, 3,…, трансфинитными числами w, w + 1,…, 2w, 2w + 1,…. В связи с различием между переменными бесконечно малыми и бесконечно большими величинами, с одной стороны, и «несобственными» бесконечно большими числами, рассматриваемыми как постоянные, ‒ с другой, возникли термины «потенциальная» Б. (для первых) и «актуальная» Б. (для вторых). В этом первоначальном понимании (о другом, современном понимании, см. ниже) спор между сторонниками актуальной и потенциальной Б. можно считать законченным. Бесконечно малые и бесконечно большие, лежащие в основе определения производной (как отношения бесконечно малых) и интеграла (как суммы бесконечно большого числа бесконечно малых) и примыкающих сюда концепций математического анализа, должны восприниматься как «потенциальные». Наряду с этим в надлежащей логической обстановке в математику вполне закономерно входят и «актуальные» бесконечно большие «несобственные» числа (и даже во многих различных аспектах: как количественные и порядковые трансфинитные числа в теории множеств, как несобственные элементы + ¥ и -¥ системы действительных чисел и т.д.).
В математике приходится иметь дело с двумя способами присоединения к числовой системе бесконечных «несобственных» элементов.
а) С проективной точки зрения на прямой находится одна «бесконечно удалённая точка». В обычной метрической системе координат этой точке естественно приписать абсциссу ¥. Такое же присоединение к числовой системе одной Б. без знака употребляется в теории функций комплексного переменного. В элементарном анализе при изучении рациональных функций
где Р (х) и Q (x) ‒ многочлены, в тех точках, где Q (x) имеет нуль более высокого порядка, чем Р (х), естественно положить f (x) = ¥. Для несобственного элемента ¥ устанавливаются такие правила действий:
¥ + а = ¥, если а конечно;
¥ + ¥ не имеет смысла;
¥ · а = ¥, если а ¹ 0;
¥ · 0 не имеет смысла.
Неравенства с участием ¥ не рассматриваются: бессмысленно спрашивать, больше или меньше ¥, чем конечное а.
б) При изучении действительных функций действительного переменного систему действительных чисел дополняют двумя несобственными элементами +¥ и -¥. Тогда можно положить, что -¥ < а < +¥ для любого конечного а, и сохранить основные свойства неравенств в расширенной числовой системе. Для +¥ и -¥ устанавливаются такие правила действий:
(+¥) + а = +¥, если а ¹ –¥;
(-¥) + а = -¥, если а ¹ +¥;
(+¥) + (-¥) лишено смысла;
(+¥) `·а = +¥, если а > 0;
(+¥) ` а = –¥, если а < 0;
(-¥) `·а = -¥, если a > 0;
(-¥) ` а = +¥, если а < 0;
(+¥) ` 0 и (¥) ` 0 лишены смысла.
В каждом математическом рассуждении следует отдавать себе отчёт, пользуемся мы в нём настоящей (не расширенной) числовой системой или расширенной, и в каком именно из двух указанных смыслов.
3) Основной интерес, но и основные трудности математического учения о Б. сосредоточиваются сейчас на вопросе о природе бесконечных множеств математических объектов. Следует, в частности, иметь в виду, что достигнутая ныне полная отчётливость и законченность теории бесконечно больших и бесконечно малых переменных величин заключается лишь в сведении всех трудностей этой теории к вопросу обоснования учения о числе, в которое существенно входит представление о Б. системы чисел. Утверждение о том, что у бесконечно мало, имеет смысл только при указании характера изменения у в зависимости от какого-либо другого переменного х; например, говорят, что у бесконечно мало при х ® а, если при любом e > 0 существует такое d > 0, что из |х – a| < d вытекает |у| < e. В самое это определение уже входит предположение, что функция y = f (x) определена для бесконечного множества значений х (например, для всех действительных х, достаточно близких к а). О бесконечных множествах в математике подробнее см. Множеств теория.
В теории множеств терминам «актуальная» и «потенциальная» Б. придают обычно глубокий смысл, не имеющий ничего общего с наименованием каждой бесконечной мощности «актуально бесконечным числом». Дело в том, что бесконечные системы математических объектов (например, натуральных или действительных чисел) никогда не задаются простым перечислением, как это возможно для конечных систем объектов. Было бы очевидным абсурдом предполагать, что кто-либо «образовал» множество натуральных чисел, перечислив их фактически «все» одно за другим. На самом деле множество натуральных чисел изучают, исходя из процесса образования его элементов переходом от n к n + 1. В случае континуума действительных чисел уже рассмотрение одного его элемента ‒ действительного числа ‒ приводит к изучению процесса образования его последовательных приближённых значений, а рассмотрение всего множества действительных чисел приводит к изучению общих свойств такого рода процессов образования его элементов. В этом именно смысле сама Б. натурального ряда, или системы всех действительных чисел (континуумы), может характеризоваться как Б. лишь «потенциальная». Точке зрения потенциальной Б. противополагается взгляд на бесконечные множества как «актуально» заданные, независимо от процесса их образования. Выяснение вопроса о том, в какой мере и при каких условиях при изучении бесконечных множеств законно такое абстрагирование от процесса их образования, ещё нельзя считать законченным. См. Множеств теория, Логика, Математика.
А. Н. Колмогоров.
Большая советская энциклопедия. — М.: Советская энциклопедия.
1969—1978.