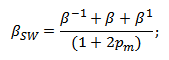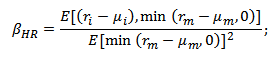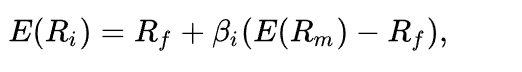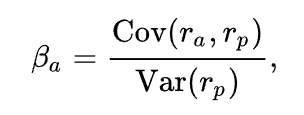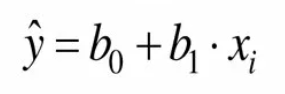Любой инвестор, когда начинает более глубоко погружаться в тему инвестирования в акции, обязательно сталкивается с таким понятием, как коэффициент бета. В данной статье мы рассмотрим следующие ключевые моменты для понимания того, что такое коэффициент бета, и как с ним стоит работать:
-
Что такое бета коэффиент акции.
-
Формула коэффициента бета.
-
Значения коэффициента бета.
-
Расчет коэффициента бета.
-
Пример расчета коэффициента бета.
-
Бета коэффициент портфеля.
Бета коэффициент акции
Коэффициент бета – это статистический коэффициент, который характеризует движение отдельной акции относительно всего рынка в целом.
Изначально бета коэффициент своими создателями задумывался как коэффициент меры риска для отдельной акции относительно всего рынка в целом, при этом для сравнения, как правило, берется динамика основного рыночного фондового индекса. Это определяется путем сравнения поведения цены акции и рыночного фондового индекса. Сравнивая различные периоды роста и падения фондового индекса и те же периоды у акции, мы можем понять, как акция вела себя в той или иной момент. Реагировала на внешние факторы так же сильно, как и рынок в целом или наоборот, акции проявляли большую устойчивость.
Формула коэффициента бета
Формула расчета коэффициента бета достаточно сложна и с чисто математической точки зрения её можно представить следующим образом:
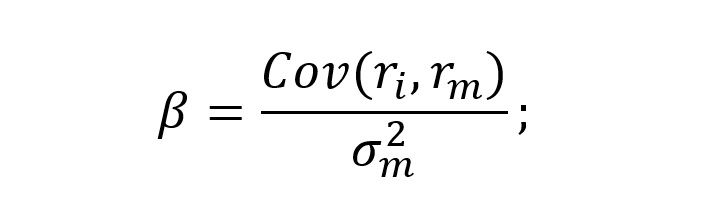
Где:
ri – доходность отдельно взятой (i-й) акции в инвестиционном портфеле за определенный период времени;
rm – доходность рынка (как правило, доходность основного фондового индекса) за определенный период времени;
σ2m – дисперсия доходности рынка (как правило, доходности основного фондового индекса) за определенный период времени.
Если же говорить по смыслу данной формулы, то в числителе находится значения зависимости (корреляции) доходности акции от доходности фондового индекса за определенный период, а в знаменателе разброс доходностей фондового индекса относительно средней доходности за определенный период.
Поэтому, исходя из данной формулы, сразу можно определить, что коэффициент бета будет давать нам представление о степени зависимости доходности акции от доходности фондового индекса, а также о том, насколько доходность отдельной акции в среднем превышает или наоборот, оказывается ниже доходности индекса.
Значения коэффициента бета
Теперь давайте разберемся в показателях коэффициента бета и как их стоит интерпретировать инвестору. Для коэффициента бета характерны несколько пороговых уровней:
-
Коэффициент бета больше 1. Это свидетельствует о том, что динамика акции коррелирует с динамикой фондового индекса, но при этом акция более чувствительно реагирует на любое движение индекса. Например, фондовый индекс растет на 1%, а акция при этом будет расти на 2% и точно так же наоборот, фондовый индекс снижается на 1%, а акция при этом снижается еще большими темпами, например, на 2%.
-
Коэффициент беты равен 1. Это говорит о том, что движения акции полностью повторяют движение фондового индекса, то есть корреляция движений акции и индекса 100%.
-
Коэффициент бета находится в диапазоне больше 0, но меньше 1. Это свидетельствует о том, что в-первую очередь динамика акции коррелирует с динамикой фондового индекса. То есть, акция движется в целом в одном направлении со всем рынком, если фондовый индекс растет, то растет и акция. Но также это говорит о том, что акция менее чувствительно реагирует на движения рынка в целом.
-
Коэффициент бета равен нулю. В данном случае такое значение коэффициента означает, что движение акции вообще никак не связано с движением фондового индекса или по-другому можно сказать, что никак не коррелируют.
-
Коэффициент бета отрицательный и находится в диапазоне от 0 до -1. В данном случае акция имеем обратную корреляцию с фондовым индексом. При этом чувствительность реакции акции более низкая, чем у фондового индекса. Например, фондовый индекс растет на 2%, при этом акция с такими показателями коэффициента бета будет снижаться, но более низкими темпами, нежели растет индекс, то есть, например, на 1%. Точно такая же ситуация справедлива и наоборот, если фондовый индекс будет снижаться на 2%, такая акция будет расти на 1%.
-
Коэффициент бета отрицательный и меньше -1. Такие акции имеют обратную корреляцию с фондовым индексом, то есть в целом движутся в противоположном направлении, при этом такие акции более волатильны и двигаются с большей амплитудой нежели сам индекс. То есть в данном случае акция будет двигаться в противоположную сторону рынку и более сильно реагировать на любые движения фондового индекса. Например, индекс растет на 1%, а акция при этом будет снижаться на 2%, и точно так же наоборот, при снижении рынка на 1%, акция с таким значением коэффициента бета будет расти на 2%.
Таким образом коэффициент бета несет для инвесторов различную ценную информацию: насколько более чувствительно реагирует акция на основные рыночные тенденции и есть ли в данной бумаге внутренняя идея, способная игнорировать общерыночные тенденции, которые охватывают своим движением большинство бумаг на рынке.
Расчет коэффициента бета
Перед большинством инвесторов тут же встает вопрос, как и где взять расчета коэффициента бета, так как формула расчета его достаточно сложна и ручной расчет его просто не представляется возможным.
Здесь стоит прежде всего сказать, что на самом деле расчет коэффициента бета на российском рынке регламентирован и стандартизирован, причем регламентирован он положением Центрального Банка “Положение о деятельности по проведению организованных торгов” (утв. Банком России 17.10.2014 N 437-П). В приложении №2 идет подробное описание расчета коэффициента бета.

Так же расчет коэффициента бета проводится непосредственно самой московской биржей по принципу, описанному в положении Центрального Банка. Коэффициент бета рассчитывается на конец каждой торговой сессии, и его расчет можно скачать на сайте Московской биржи https://www.moex.com/ru/forts/coefficients-values.aspx
При этом, как мы видим из формулы расчета коэффициента, что он рассчитывается за период последних 30-и торговых сессий.
Расчет коэффициента бета происходит точно так же, как и расчет многих технических индикаторов рынка, то есть по принципу скользящего окна, когда в расчетный диапазон коэффициента попадают лишь только 30 последних ценовых значений, и данный диапазон постоянно сдвигается, как только в расчет попадет котировка новой торговой сессии.
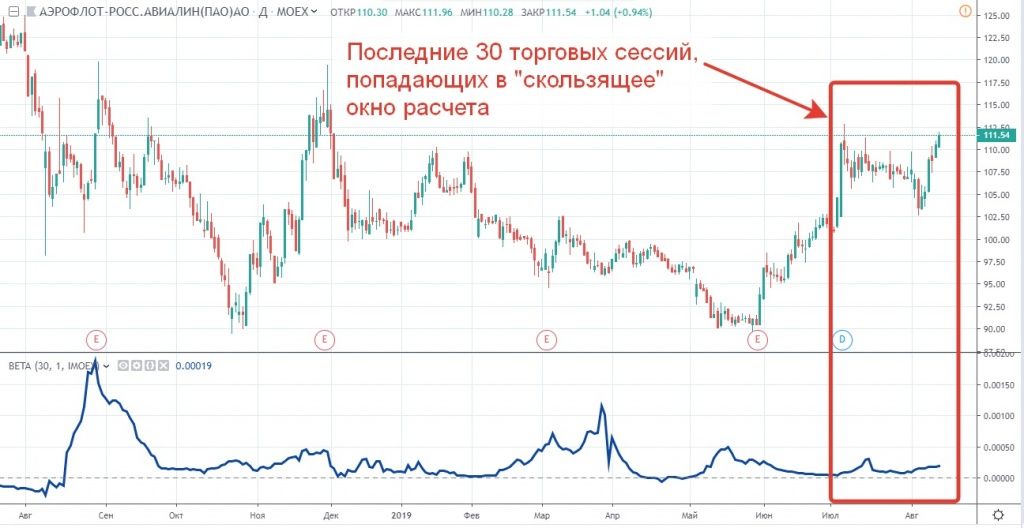
За счет того, что период расчета коэффициента бета сравнительно мал, с инвестиционной точки зрения, это приводит к тому, что значения коэффициента очень волатильны и сильно изменяются во времени. Иногда значение коэффициента от одного месяца к другому может изменяться кардинально, как с точки зрения характеризующей корреляцию акции и индекса, так и с точки зрения степени чувствительности реакции акции на движения индекса. Это можно заметить даже просто по скользящему графику расчета коэффициента, так как во времени он изменяется очень активно и очень резко.
Иными словами, рассчитанные подобным образом значения коэффициента бета, отражают лишь локальные и очень краткосрочные рыночные тенденции, которые не отражают в полной мере заложенных фундаментальных принципов в данный коэффициент.
Изначально коэффициент бета разрабатывался и применялся исключительно в инвестиционных целях и активно использовался для формирования инвестиционных портфелей, в том числе портфелей по модели «Марковица». С этой точки зрения, расчет коэффициента за такой короткий промежуток времени полностью некорректен и не может применяться с инвестиционными целями.
Однако, корректный расчет показателя бета можно сделать даже с помощью инструментов MS Excel, именно такой калькулятор для расчета коэффициента бета мы и реализовали в рамках нашего курса обучения «Школа разумного инвестирования».
Для того чтобы коэффициент бета отражал именно долгосрочные инвестиционные тенденции в акциях, мы должны прибегать к его расчету за более длительные горизонты от 3-х лет.
Пример расчета бета коэффициента
Проведем расчет коэффициента бета на различных бумагах за более длительный промежуток времени с помощью калькулятора для расчета бета коэффициента.
Для расчета мы выберем акции с потенциально бОльшим и потенциально меньшим коэффициентом бета. В качестве примера более агрессивно движущейся акции, которая имеет положительную корреляцию с рынком, мы возьмем обыкновенные акции Сбербанка, а в качестве примера бумаги, которая не зависит от колебаний рынка в целом и демонстрирует самостоятельную динамику, мы возьмем привилегированные акции компании Ленэнерго.
В калькуляторе заполняются поля с датами торговых периодов за последние 3 года, значения дневных цен закрытия по акции за последние 3 года, а также значения фондового индекса на конец торговой сессии за последние 3 года.
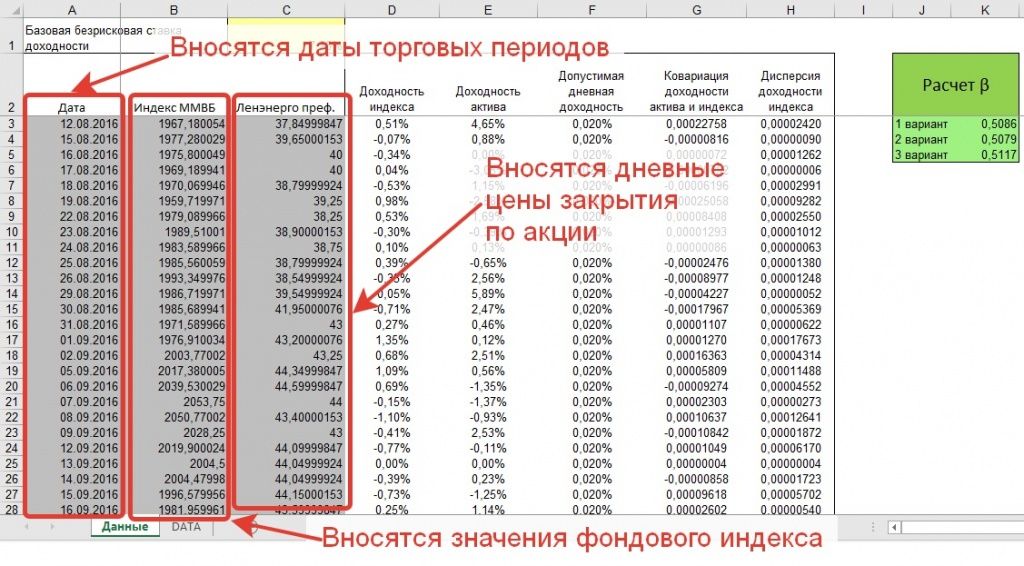
Расчет коэффициента бета в калькуляторе проводится тремя различными способами для подтверждения статистической достоверности расчета коэффициента.
После заполнения данных по котировкам акций Сбербанка и индекса московкой биржи за последние 3 года, мы видим, что значение коэффициента бета по бумаге оказывается большим чем 1.
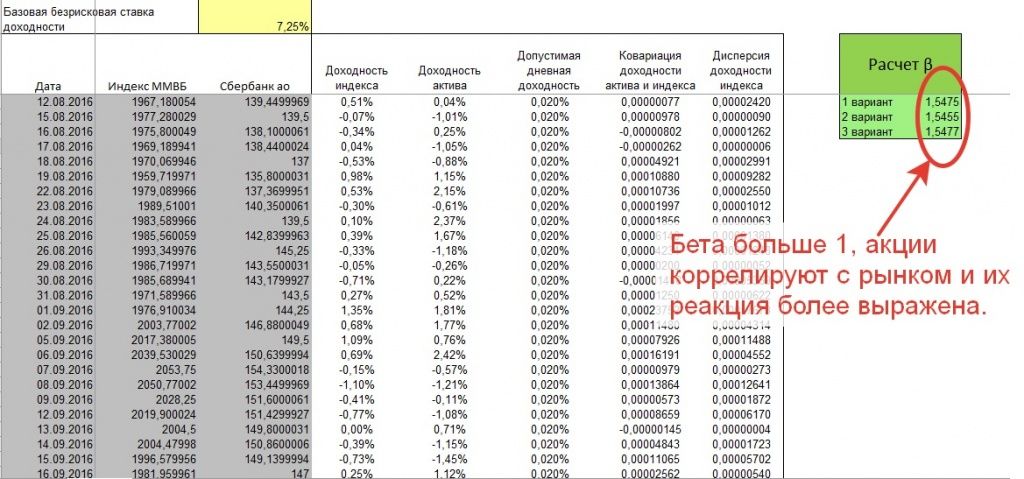
Положительное значение коэффициента бета по акциям Сбербанка говорит нам о том, что акции преимущественно движутся в том же направлении, что и рынок в целом, а значение коэффициента больше 1 свидетельствуют о том, что акции намного более сильно реагируют на рыночные движения.
Во втором случае мы так же проводили расчет коэффициента бета за последние 3 года по привилегированным акциям Ленэнерго.
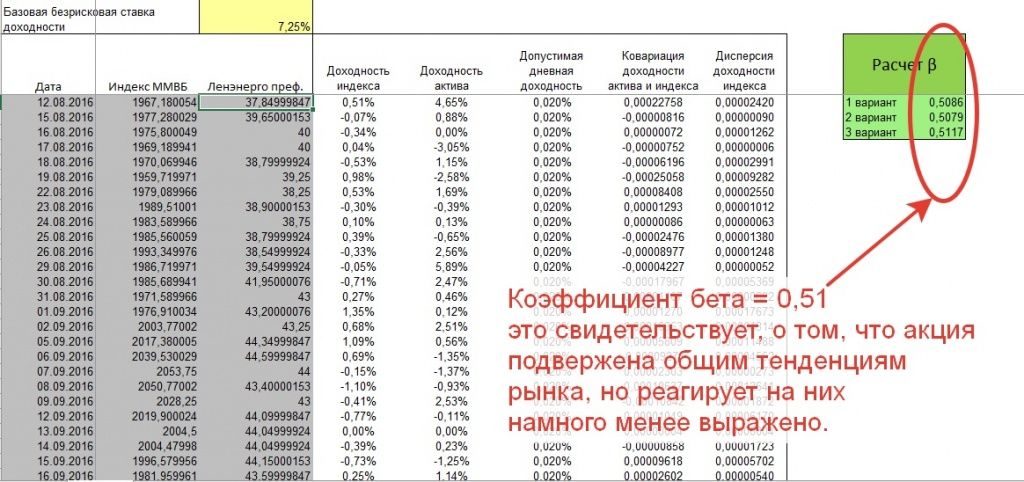
В данном случае значение коэффициента бета оказывается равным 0,51, что свидетельствует о том, что в целом акция не движется в противофазе рынку и лишь частично подвержена влияниям основных общерыночных тенденций.
Бета коэффициент портфеля (практика применения)
Использование коэффициента бета при формировании портфеля и в процессе управление инвестиционным портфелем – это одна из основных, базовых практик портфельного инвестирования, так как значение корректно рассчитанного коэффициента отражает то, как бумага за счет своих внутренних фундаментальных свойств «отрабатывает» движения общерыночных тенденций. Особенно в этом ключе важно понимание того, что под общерыночными тенденциями мы в первую очередь, как правило, подразумеваем общие негативные движения рынка, или проявление кризисных моментов на рынке, которые влияют на все акции. Когда большинство акций на рынке снижается, те бумаги, которые способны противостоять общерыночному снижению, представляют особенную ценность для инвестиционного портфеля.
Поэтому коэффициент бета в инвестиционных портфелях, как правило, в первую очередь может применяться, как весовой коэффициент, который распределяет средства портфеля в акции в зависимости от степени чувствительности к риску той или иной акции.
При этом, в случае, если основная концепция инвестиционного портфеля требует максимальной минимизации риска, то за счет бета коэффициента придается больший вес бумагам с малым значением коэффициента бета, или даже с его отрицательным значением. А в случае, если формируется агрессивный инвестиционный портфель, то веса распределяются наоборот. Акции с большим значением коэффициента бета получают больший вес в инвестиционном портфеле. Это позволяет добиться того, что на фазе роста фондового рынка, акции, включенные в инвестиционный портфель, реагируют более выражено и растут большими темпами, в итоге, это позволяет такому портфелю обгонять фондовый индекс по показателям доходности.
Как работает коэффициент бета мы можем увидеть даже визуально, наложив котировки акции, на значения фондового индекса.
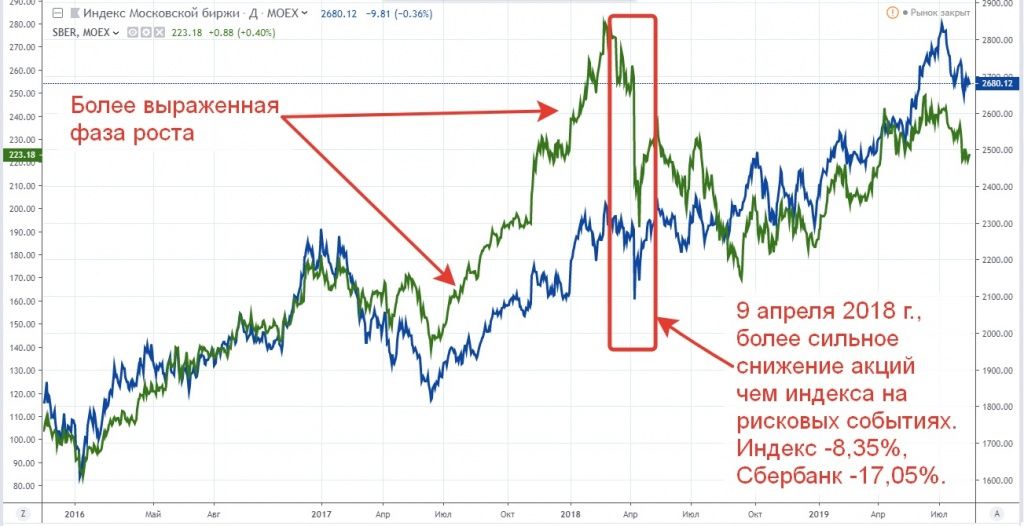
В случае с акцией Сбербанка, где коэффициент бета больше 1, мы можем наблюдать, что поведение бумаги более агрессивное, и если рынок растет, то бумаги растут еще большими темпами, а на коррекционных фазах мы видим, что просадки по акциям случаются более значительные чем по рынку в целом.
И практически противоположную картину мы можем увидеть в акциях с коэффициентом бета меньше 1.
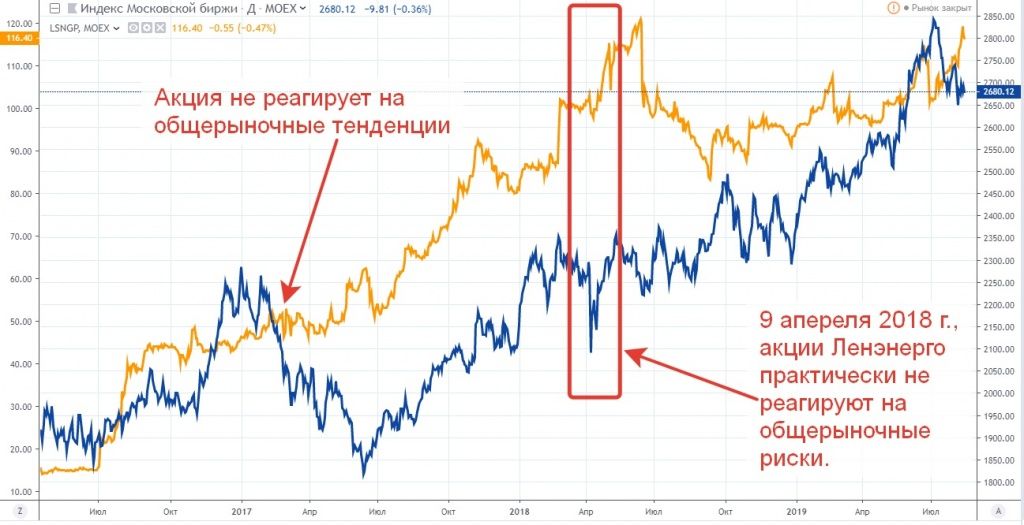
В нашем примере акции Ленэнерго преф. в момент острейшего проявления кризисных моментов на рынке демонстрировали высокую степень устойчивости и практически никак не реагировали на общерыночные тенденции. Поэтому акции, значение коэффициента бета которых меньше 1, так же еще причисляют к категории защитных бумаг, которые способны эффективно противостоять общерыночным негативным тенденциям.
Выводы
Как мы видим, коэффициент бета может быть очень эффективным и полезным инструментом при формировании инвестиционного портфеля, но только с учетом того, что инвесторы корректно определяют его значение и грамотно его используют.
Всему этому мы учим на нашем полном цикле курсов обучения «Школа разумного инвестирования». Начать обучение можно с посещения вводных бесплатных занятий. Записаться на ближайший бесплатный вебинар можно по ссылке – http://finplan.expert
Удачных Вам инвестиций!
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Привет! Что значат альфа и бета в портфельной теории? Нужно ли их учитывать простому инвестору при составлении стратегии?
Альфа и бета — это показатели для оценки эффективности инвестиций. Альфа измеряет доходность актива или портфеля активов в сравнении с рынком, а бета — волатильность, то есть риск относительно рынка.
Оба показателя — исторические. Значит, они зависят от выбранного временного отрезка и не гарантируют результат в будущем. Рассмотрим их подробнее.
Что такое бета портфеля
В основе традиционного подхода к инвестированию лежит современная теория портфеля, которую предложил Гарри Марковиц в 1952 году.
Чтобы получить оптимальный портфель, используют комбинацию инструментов со слабой или отрицательной взаимосвязью — корреляцией. Тогда потери по одному активу будут компенсироваться прибылью от других. И можно подобрать идеальную смесь инструментов, которая минимизирует риск при заданной ожидаемой доходности.
Коэффициент «бета» как раз и нужен для оценки риска. Этот параметр предложил Уильям Шарп в 1964 году. Бета считается первым фактором в теории факторного инвестирования.
Бета дает представление о капризности цены отдельного актива или всего портфеля относительно эталона — бенчмарка. В роли бенчмарка обычно выступает биржевой индекс на широкий рынок. Для американских акций бета измеряется относительно индекса S&P 500, для российских акций ориентиром служит индекс Мосбиржи.
Бета дает представление о том, принял на себя инвестор повышенный риск относительно широкого рынка или нет. Например, бета актива 0,5 означает, что при движении S&P 500 на 10% цена актива сдвинется в ту же сторону на половину от этого значения, то есть на 5%. Таким образом, речь идет о низкорисковом активе.
Вот как интерпретируют значения беты:
- Бета < −1. Корреляция актива и бенчмарка обратная, то есть они движутся разнонаправленно, при этом актив более волатилен.
- −1 < бета < 0. Корреляция по-прежнему обратная, но актив ведет себя стабильнее бенчмарка.
- 0 < бета < 1. Актив движется однонаправленно с бенчмарком, но колеблется не так сильно, риск меньше рыночного.
- Бета > 1. Актив коррелирует с индексом и более волатилен, то есть он очень рисковый.
Отрицательная бета встречается относительно редко.
Как посчитать бету актива. Бета — статистический параметр. Она показывает направление и амплитуду цены только на заданном историческом отрезке.
Как посчитать бету портфеля. Бета портфеля — это сумма показателей беты каждого актива, умноженная на вес актива.
Предположим, портфель инвестора состоит из четырех активов с равным весом, но с разной бетой.
Портфель из активов с разными бета-коэффициентами
| Актив | Доля | Бета |
|---|---|---|
| Актив А | 25% | 1 |
| Актив Б | 25% | 1,6 |
| Актив В | 25% | 0,75 |
| Актив Г | 25% | 0,5 |
Посчитаем общую бету портфеля: 25% × 1 + 25% × 1,6 + 25% × 0,75 + 25% × 0,5 = 0,96. Значение приближено к 1 — значит, риск портфеля сопоставим с риском бенчмарка и движутся они однонаправленно.
Предположим, инвестор хочет получить доходность больше и готов взять на себя дополнительный риск — его устроит бета портфеля 1,2. Тогда он может скорректировать доли, например, так: забрать 5 п. п. от актива А и по 10 п. п. от активов В и Г в пользу самого рискового инструмента — Б.
Новая бета портфеля будет: 20% × 1 + 50% × 1,6 + 15% × 0,75 + 15% × 0,5 = 1,19
Если же нужна консервативная стратегия, тогда надо искать набор активов с бетой меньше 1, но и ожидаемая доходность от инвестиций будет ниже.
Еще вариант посчитать бету вместе с другими популярными метриками — воспользоваться сервисом Portfolio Visualizer для бэктеста портфеля на исторических данных. Для примера рассмотрим параметры портфеля из четырех активов в период с января по конец июля 2022 года.
Показатели портфеля из четырех активов в сравнении с бенчмарком за январь — июль 2022 года
| Актив | Доля | Среднегодовая волатильность | Среднегодовая доходность | Корреляция с S&P 500 |
|---|---|---|---|---|
| Apple, APPL | 25% | 34,82% | −8,23% | 0,91 |
| Exxon Mobil, XOM | 25% | 37,83% | 61,81% | 0,33 |
| Merck, MRK | 25% | 18,89% | 18,57% | −0,24 |
| Золото, GLD | 25% | 11,31% | −4,01% | 0 |
| Портфель | — | 18,05% | 18,98% | 0,66 |
| Бенчмарк — S&P 500, SPY | — | 22,71% | −12,65% | 1 |
Показатели портфеля из четырех активов в сравнении с бенчмарком за январь — июль 2022 года
Среднегодовая волатильность
34,82%
Среднегодовая доходность
−8,23%
Корреляция с S&P 500
0,91
Среднегодовая волатильность
37,83%
Среднегодовая доходность
61,81%
Корреляция с S&P 500
0,33
Среднегодовая волатильность
18,89%
Среднегодовая доходность
18,57%
Корреляция с S&P 500
−0,24
Среднегодовая волатильность
11,31%
Среднегодовая доходность
−4,01%
Среднегодовая волатильность
18,05%
Среднегодовая доходность
18,98%
Корреляция с S&P 500
0,66
Среднегодовая волатильность
22,71%
Среднегодовая доходность
−12,65%
На вкладке Metrics сервис отобразит разные коэффициенты портфеля, в том числе бету. Для нашего портфеля она 0,55. Таким образом, этот портфель в указанный период был менее рисковым, чем индекс, и при этом дал высокую доходность, в то время как широкий рынок упал.
Но стоит учесть, что это была ограниченная выборка на коротком временном отрезке и в будущем активы, вероятно, поведут себя иначе. Поэтому для более объективной картины лучше тестировать портфель и сравнивать его с бенчмарком на горизонте 10—30 лет. Так можно будет сделать более правильные выводы, но даже это не будет гарантировать хороший результат.
Что такое альфа портфеля
Развитие портфельной теории показало, что на практике доходность инвестиций не объяснить одной только бетой. Нередко портфели показывали результат выше ожиданий.
Эту сверхдоходность или избыточную доходность стали списывать на эффект от портфельного управления — альфу. Например, она могла заключаться в том, что инвестор грамотно определил точку входа и купил актив на самом дне.
Но в этом случае стояла проблема, как отделить фактор действий инвестора от премии за риск, ведь сверхдоходность могла быть еще результатом принятия на себя большего риска.
В 1968 году Майкл Дженсен представил формулу для расчета избыточной доходности портфеля с поправкой на риск:
Альфа Дженсена = pr − (rf + b × (rm − rf)),
где:
pr — доходность портфеля;
b — бета портфеля;
rm — показатель бенчмарка;
rf — безрисковая ставка.
В США за безрисковую ставку обычно принимают доходность одно-трехмесячных казначейских облигаций США. Последние расцениваются как денежный эквивалент, и их бета близка к нулю: инвестор не рискует, но и не получает ощутимого дохода.
Рассмотрим на примере. Пусть доходность портфеля — 20% при бете 1,12, а доходность бенчмарка и безрисковая ставка — 11 и 2%.
Считаем: 20 − (2 + 1,12 × (11 − 2)) = 7,92%. То есть доходность инвестиций превосходит рынок.
Рассчитывать альфу самому необязательно: в интернете есть калькуляторы. Еще она отображается в «Метриках» в сервисе Portfolio Visualizer.
Как видите, в отличие от просто разницы доходности между портфелем и бенчмарком, сверхдоходность портфеля корректируется на риск с помощью беты. Это позволяет лучше оценить эффективность инвестиций.
Высокая альфа — всегда хорошо. Отрицательная альфа означает, что мы проиграли рынку. А нулевая альфа будет, например, если инвестор пассивно вкладывает в индекс: через соответствующий ETF или самостоятельно копирует состав индекса и своевременно ребалансирует его.
Особенно показатель альфы важен для портфельных менеджеров, так как позволяет оценить эффективность их работы.
При расчете альфы может учитываться результат других факторов инвестирования, помимо беты, например дивидендный, стоимостной факторы и так далее. Это помогает понять, откуда взялась избыточная доходность. Например, по исследованию AQR Capital Management, у Баффетта заметная альфа относительно традиционных факторов, но, если учесть эффект факторов типа betting against beta, альфа снижается.
Что в итоге
Бета позволяет оценить риск инвестиций и понять, насколько актив или портфель в целом волатилен в сравнении с рынком.
Бета — первый фактор инвестирования, но впоследствии определили еще много факторов, от которых зависит результат инвестиций.
В портфельной теории Марковица рынок эффективен, и чем больше риск инвестиций, тем выше ожидаемая доходность. Но в реальности бета непредсказуема и доходность акций может оказаться даже ниже безрисковой ставки. Так, в период с 2000 по 2009 год акции США принесли инвесторам убыток и были хуже облигаций и наличных.
Альфа позволяет измерить избыточную доходность относительно бенчмарка с поправкой на риск. Она отражает удачные действия инвестора и хороший тайминг сделок.
Простому инвестору стоит оценить бету при составлении стратегии, чтобы понимать риск инвестиций и оптимизировать ожидаемую доходность.
Что касается альфы, она очень важна для профессиональных портфельных управляющих, но простому инвестору можно не брать ее в расчет, особенно если он инвестирует в индексы и делает это пассивно — по принципу «купил и держи».
На чтение 9 мин Просмотров 99.6к.
Разберем такой инвестиционный показатель как – коэффициент бета, рассчитаем его на реальном пример с помощью Excel и рассмотрим различные современные модификации.
Содержание
- Инфографика: Коэффициент бета
- Коэффициент бета. Определение
- Формула расчета коэффициента бета
- Анализ уровня риска по значению коэффициента бета (β)
- Данные для построения коэффициента бета информационными компаниями
- Коэффициент бета в модели оценки капитальных активов –CAPM
- Пример расчета коэффициента бета вExcel
- Недостатки использования коэффициента бета в модели CAPM
- Модификация коэффициента бета
- Коэффициент бета для акций США
- Где посмотреть коэффициент бета для российских акций
Инфографика: Коэффициент бета
Коэффициент бета. Определение
Коэффициент бета (англ. Beta, β, beta coefficient) – определяет меру риска акции (актива) по отношению к рынку и показывает чувствительность изменения доходности акции по отношению к изменению доходности рынка. Коэффициент бета может быть рассчитан не только для отдельной акции, но также и для инвестиционного портфеля. Коэффициент используется как мера систематического риска, и применяется в модели У.Шарпа – оценки капитальных активов CAPM (Capital Assets Price Model). В первые, коэффициент бета рассмотрел Г. Марковиц для оценки систематического риска акций, который получил называние индекс недиверсифицируемого риска. Коэффициент бета позволяет сравнивать между собой акции различных компаний по степени их риска.
Формула расчета коэффициента бета
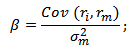
β – коэффициент бета, мера систематического риска (рыночного риска);
ri – доходность i-й акации (инвестиционного портфеля);
rm – рыночная доходность;
σ2m – дисперсия рыночной доходности.
Анализ уровня риска по значению коэффициента бета (β)
Коэффициент бета показывает рыночный риск акции и отражает чувствительность изменения акции по отношению к изменению доходности рынка. В таблице ниже показана оценка уровня риска по коэффициенту бета. Коэффициент бета может иметь как положительный, так и отрицательный знак, который показывает положительную или отрицательную корреляцию между акцией и рынком. Положительный знак отражает, что доходность акций и рынка изменяются в одном направлении, отрицательный – разнонаправленное движение.
|
Значение показателя |
Уровень риска акции |
Направление изменения доходности акции |
|
β > 1 |
Высокий |
Однонаправленное |
|
β = 1 |
Умеренный |
Однонаправленное |
|
0 < β < 1 |
Низкий |
Однонаправленное |
| -1 < β < 0 |
Низкий |
Разнонаправленное |
| β = -1 |
Умеренный |
Разнонаправленное |
|
β < -1 |
Высокий |
Разнонаправленное |
Данные для построения коэффициента бета информационными компаниями
Коэффициент бета используется многими информационно-инвестиционными компаниями для оценки систематического риска: Bloomberg, Barra, Value Line и др . Для построения коэффициента бета используются месячные/недельные данные за несколько лет. В таблице показаны основные параметры оценки показателя различными информационными компаниями.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
|
Информационные компании |
Исторический период наблюдения | Частота |
|
Bloomberg |
2 года |
Неделя |
| Barra | 5 лет |
Месяц |
| Value Line | 5 лет |
Месяц |
Можно заметить, что Bloomberg проводит краткосрочную оценку показателя, тогда как Barra и Value Line используют месячные данные доходностей акций и рынка за последние пять лет. Долгосрочная оценка может сильно быть искажена вследствие влияния на акции компании различных кризисов и негативных факторов.
Коэффициент бета в модели оценки капитальных активов – CAPM
Формула расчета доходности акций по модели капитальных активов CAPM (Capital Assets Price Model, модель У.Шарпа) имеет следующий вид:
где:
r – будущая ожидаемая доходность акций компании;
rf – доходность по безрисковому активу;
rm – доходность рынка;
β – коэффициент бета (мера рыночного риска), отражает чувствительность изменения стоимости акций компании в зависимости от изменения доходности рынка (индекса);
Модель CAPM была создана У.Шарпом (1964) и Дж. Линтером (1965) и позволяет спрогнозировать будущее значение доходности акции (актива) на основании линейной регрессии. Модель отражает линейную взаимосвязь планируемой доходности с уровнем рыночного риска, выраженного коэффициентом бета.
Доходность по безрисковому активу, на практике, берется как доходность по государственным ценным бумагам ГКО, ОФЗ. Доходность по ним в России составляет около 12%. Доходность можно посмотреть на сайте ЦБ в разделе «Ставки рынка ГКО-ОФЗ».
Для расчета рыночной доходности используют доходность индекса или фьючерса на индекс (индекс ММВБ, РТС – для России, S&P500 – США).
Пример расчета коэффициента бета в Excel
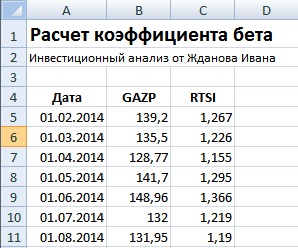
Рассчитаем коэффициент бета в Excel для отечественной компании ОАО «Газпром». Данная компания имеет обыкновенные акции, котировки которых можно посмотреть на сайте finam.ru в разделе «Экспорт данных». Для расчета были взяты месячные котировки акции ОАО «Газпром» (GAZP) и индекса РТС (RTSI) за период с 31.01.2014 по 31.01.2015 г.
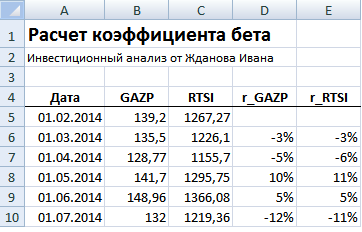
Далее необходимо рассчитать доходности по акции и индексу, для этого воспользуемся формулами:
D6=LN(B6/B5)
E6=LN(C6/C5)
Для расчета коэффициента бета необходимо рассчитать коэффициент линейной регрессии между доходностью акций ОАО «Газпром» и индекса РТС. Рассмотрим два варианта расчета коэффициента бета средствами Excel.
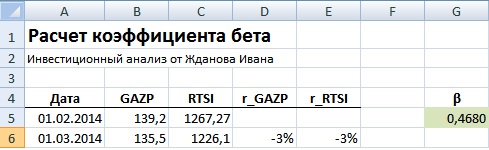
Вариант №1. Расчет через формулу Excel
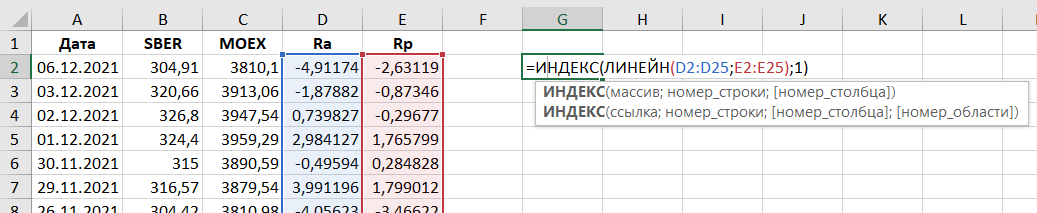
Расчет через формулы Excel выглядит следующим образом:
=ИНДЕКС(ЛИНЕЙН(D6:D17;E6:E17);1)
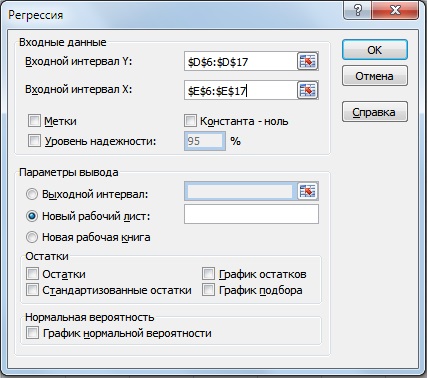
Вариант №2. Расчет через надстройку «Анализ данных»
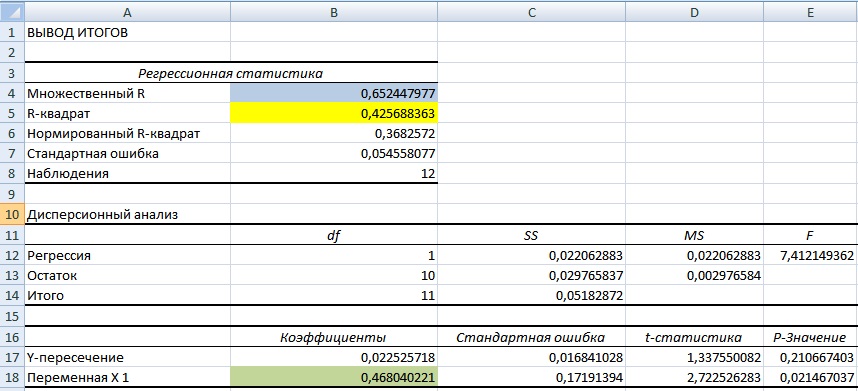
Второй вариант расчета коэффициента бета использует надстройку Excel «Анализ данных». Для этого необходимо перейти в главном меню программы в раздел «Данные», выбрать опцию «Анализ данных» (если данная надстройка включена) и в инструментах анализа выделить «Регрессия». В поле «Входной интервал Y» выбрать доходности акции ОАО «Газпром», а в поле «Выходные интервал X» выбрать доходности индекса РТС.
Далее мы получим отчет по регрессии на отдельном листе. В ячейке В18 показано значение коэффициента линейной регрессии, который равен коэффициенту бета = 0,46. Также проанализируем другие параметры модели, так показатель R-квадрат (коэффициент детерминированности) показывает силу взаимосвязи между доходностью акции ОАО «Газпром» и индекса РТС. Коэффициент детерминированности равен 0,4, что является довольно мало для точного прогнозирования будущей доходности по модели CAPM. Множественный R – коэффициент корреляции (0,6), который показывает наличие зависимости между акцией и рынком.
Значение 0,46 коэффициента бета для акции свидетельствует о умеренном риске и в тоже время сонаправленность изменения доходностей.
Недостатки использования коэффициента бета в модели CAPM
Рассмотрим ряд недостатков присущих данному коэффициенту:
- Сложность использования коэффициента бета для оценки низколиквидных акций. Данная ситуация характерна для развивающихся рынков капитала, в частности: России, Индии, Бразилии и т.д.
- Не возможность оценки малых компаний, не имеющих эмиссий обыкновенных акций. Большинство отечественных компаний не проходили процедуры IPO.
- Неустойчивость прогноза коэффициента бета. Использование линейной регрессии для оценки рыночного риска по ретроспективным данным не позволяет получать точные прогнозы риска. Как правило, трудно прогнозировать коэффициент бета более 1 года.
- Не возможность учета несистематических рисков компании: рыночной капитализации, исторической доходности, отраслевой принадлежности, критериев P/E и т.д., которые оказывает влияние на величину ожидаемой доходности.
Модификация коэффициента бета
Так как коэффициент, предложенный У. Шарпов не имел должной устойчивости и не мог использоваться для прогнозирования будущей доходности в модели CAPM, различными учеными были предложены модификации и корректировки данного показателя (англ. adjusted beta, modified beta).Рассмотрим скорректированные коэффициенты бета:
Модификация коэффициента бета от М.Блюма (1971)
Маршал Блюм показал, что со временем коэффициенты бета компаний стремятся к 1. Формула расчета скорректированного показателя следующая:
Использование данных весовых значений позволяет более точно спрогнозировать будущий систематический риск. Так данную модификацию используют многие информационные агентства, такие как: Bloomberg, Value Line и Merrill Lynch.
Модификация коэффициента бета от Бава-Линдсберга (1977)
В своей корректировке Линдсберг предложил рассчитывать односторонний коэффициент бета. Главный постулат заключался в том, что изменение доходности выше определенного уровня большинство инвесторов не рассматривают как риск, а риском считается только то, что ниже уровня. За минимальный уровень риска в данной модели был доходность безрискового актива.
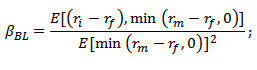
ri – доходность акции; rm – доходность рынка; rf – доходность безрискового актива.
Модификация коэффициента бета от Шоулза-Виллимса
β-1, β, β1 – коэффициенты беты для предыдущего (-1) текущего и следующего (1) периода;
ρm – коэффициент автокорреляции рыночной доходности.
Модификация коэффициента бета от Харлоу-Рао (1989)
Формула отражает одностороннюю бету, с предположением, что инвесторы рассматривают риск только как отклонение от среднерыночной доходности вниз. В отличие от модели Бава-Линдсберга за минимальный уровень риска брался уровень среднерыночной доходности.
где: μi – средняя доходность акции; μm – средняя доходность рынка;
Помимо коэффициента бета на практике используют другие показатели риска-доходности инвестиционного портфеля, ПИФа, более подробно узнать про современные показатели оценки инвестиций вы можете в моей статье: «Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel«. О практике оценке риска инвестиции читайте в статье: «Методы оценки риска VaR (Value at Risk). Рыночный риск. Пример расчета в Excel «.
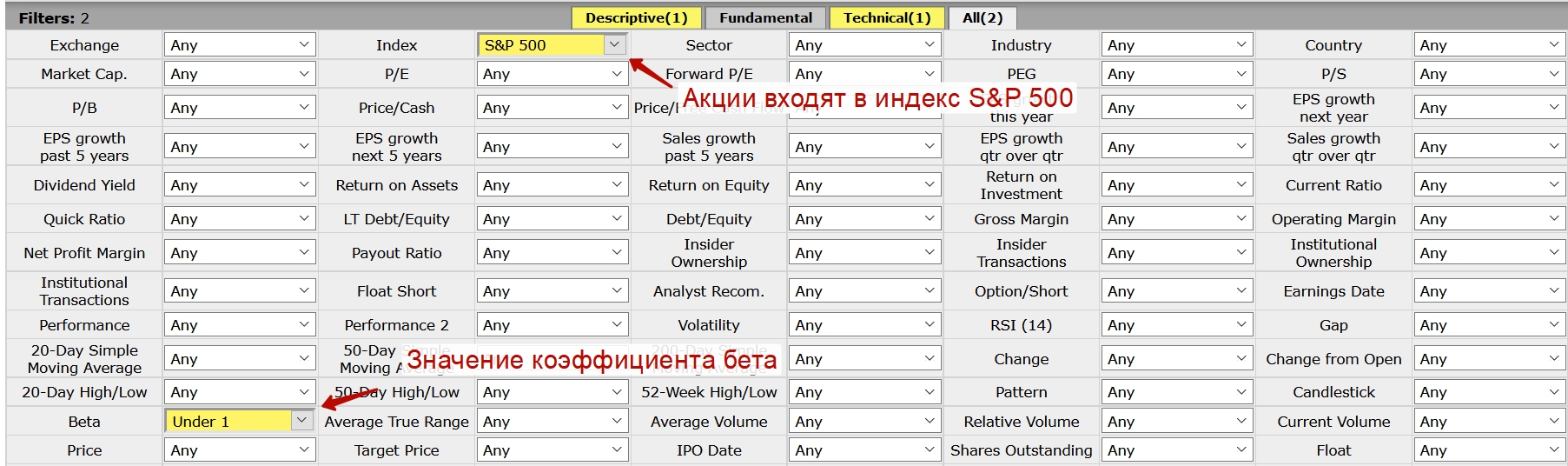
Коэффициент бета для акций США
Существуют сервисы позволяющие оценить коэффициент бета для множества компаний и выделить наиболее интересные. Будем применять сервис Finviz. Чтобы найти акции менее чувствительные чем колебания фондового рынка необходимо установить коэффициент бета меньше 1.
Где посмотреть коэффициент бета для российских акций
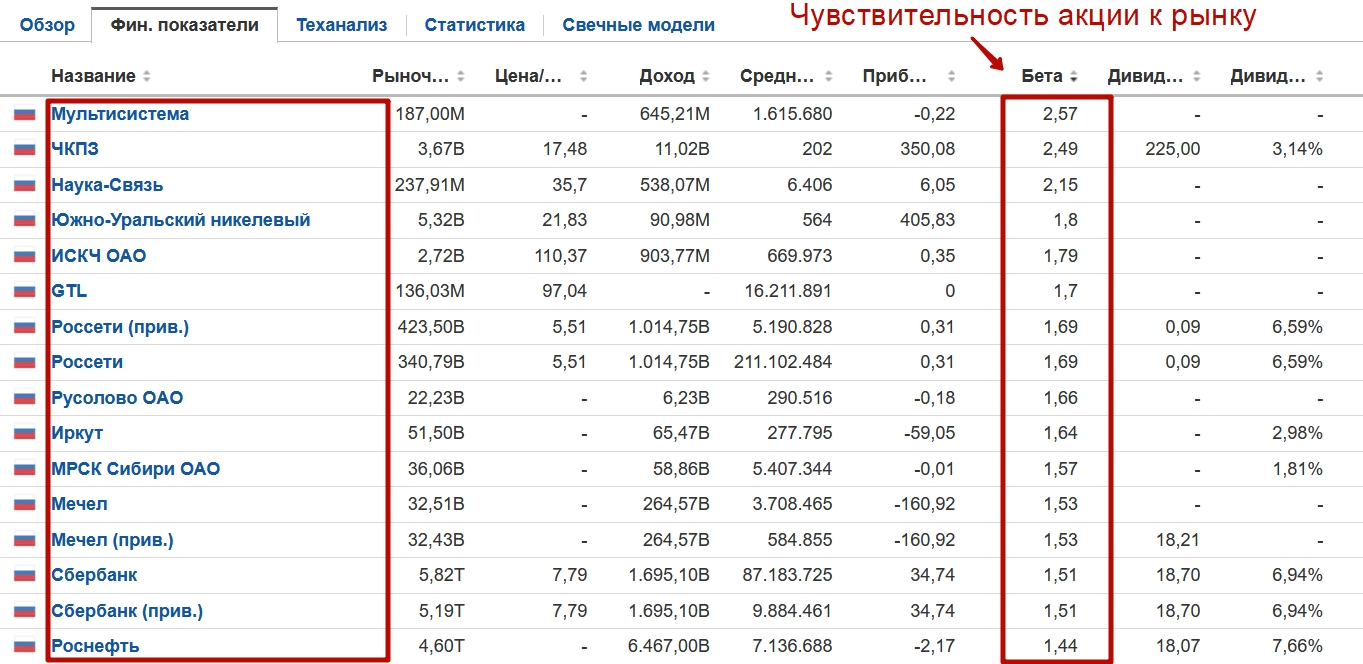
Если цель узнать коэффициент бета для российских акций, то для этого можно воспользоваться сервисом investing.com. Помимо отечественных компаний коэффициент бета можно определить для иностранных. Как мы видим для акции Мультисистемы коэффициент равен 2,57 – это значит, что она в 2,5 раза более изменчивая по отношению к рыночному изменению (индексу ММВБ).
Проанализировать акции на бета можно по ссылке.
Высокие значения коэффициента бета при растущем рынке будут обеспечивать дополнительную прибыль, при коррекциях такие акции как правило имеют больше убытков.
Резюме
Коэффициент бета является одним из классических мер рыночного риска для оценки доходности акций, инвестиционных портфелей и ПИФов. Несмотря на сложность использования данного инструмента для оценки отечественных низколиквидных акций и неустойчивость его изменения во времени, коэффициент бета является ключевым показателем оценки инвестиционных рисков. Рассмотренные модификации коэффициента позволяют скорректировать и дать более оценку систематическому риску. С вами был Иван Жданов, спасибо за внимание.
Автор: к.э.н. Жданов Иван Юрьевич
При оценке компании доходным методом, то есть путем дисконтирования будущих денежных потоков, очевидно значимым моментом является определение ставки дисконтирования, с помощью которой эти самые будущие денежные потоки будут приводиться к текущей стоимости.
Не вдаваясь в подробности расчета дисконтированных денежных потоков, скажу, что базово потоки делятся на два вида: денежные потоки на собственный капитал и денежные потоки на инвестированный капитал (собственный капитал + заемное финансирование). Отличаются и ставки дисконтирования для двух разновидностей потоков. Поскольку речь далее пойдет про смысл и методику расчета коэффициента бета, то обратимся к ставке дисконтирования для собственного капитала. Она, к слову, нужна и для расчета ставки дисконтирования для капитала инвестированного.
В современной практике для расчета ставки дисконтирования денежный потоков на собственный капитал в большинстве случаев применяется модель CAPM (Capital Asset Pricing Model), что в дословном переводе означает «модель ценообразования капитальных активов».
Концепция CAPM была разработана на основе портфельной теории Г. Марковица, наиболее применимая на сегодняшний день интерпретация данной концепции принадлежит У. Шарпу, поэтому она зачастую называется его именем. Ставка доходности, рассчитанная по модели CAPM, определяет, какой должна быть доходность актива, добавляемого к портфелю, с учетом его рыночного риска. Поскольку именно требуемой доходностью определяется ставка дисконтирования будущих денежных потоков, рассчитанная по описываемой модели доходность может использоваться в качестве такой ставки. Рассчитанная по модели CAPM требуемая норма доходности в отношении актива является, таким образом, общей для рынка, то есть лишена субъективной составляющей.
Ниже приведена формула расчета доходности по CAPM:
Где:
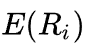
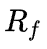
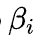
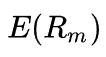
Выражение в скобках представляет собой премию за риск для определенного рынка (рынка, для которого мы берем рыночную доходность и безрисковую ставку). Бета-коэффициент, таким образом, выступает мерой рыночного риска: он определяет, в какой степени конкретный актив подвержен рыночному риску, то есть как соотносится изменение доходности актива с изменением доходности рыночного портфеля.
Поскольку доходность актива в случае с акциями определяется движением котировок, коэффициент бета также часто интерпретируют как волатильность: чем выше коэффициент – тем волатильнее акция, для которой он рассчитан. Волатильность же измеряется в данном случае относительно рыночного портфеля.
Расчет бета-коэффициента:
Где:
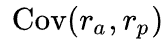
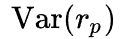
Коэффициент бета, таким образом, может принимать любое значение, однако чаще всего находится в диапазоне от -1 до 1, или, еще чаще, в диапазоне от 0 до 1. Ниже приведена интерпретация основных интервалов значений.
-
Бета 0. Такое значение коэффициента означает, что доходность актива не изменяется вовсе, то есть он является безрисковым. Если подставить такое значение в первую формулу, мы получим доходность, равную безрисковой ставке.
-
Бета в диапазоне от 0 до 1. Такое значение коэффициента означает, что доходность актива и рыночного портфеля изменяются сонаправленно, однако изменение доходности актива (волатильность) ниже, чем у рыночного портфеля.
-
Бета равна 1. Означает, что доходности актива и рыночного портфеля меняются одинаково, то есть корреляция 100%.
-
Бета коэффициент больше 1. Означает, что доходность актива и рыночного портфеля меняются сонаправленно, однако изменчивость доходности актива выше, нежели рыночного портфеля. То есть, выше его риск.
-
Бета в диапазоне от -1 до 0. Выводы аналогичны диапазону от 0 до 1, однако движение доходностей является противоположным.
-
Бета равна -1. Означает, что доходности актива и рыночного портфеля изменяются в одинаковой мере, но разнонаправленно.
-
Бета меньше -1. Выводы аналогичны значению больше 1, однако движение доходностей разнонаправленное.
Поскольку, как сказано выше, доходность определяется движением котировок, под изменением доходности следует понимать изменение котировок.
Как рассчитать бета-коэффициент?
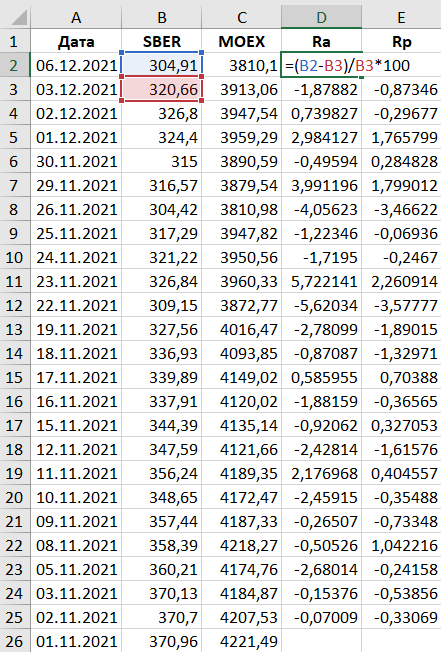
Поскольку расчет бета-коэффициента – достаточно трудоемкое занятие, сегодня это проще всего сделать с помощью Excel. В таблице ниже для примера взяты данные по торгам с 1 ноября 2021 года, однако на практике лучше использовать более длительный период, хотя бы от 100 торговых дней.
Для каждого периода рассчитываем доходности Ra (доходность акции) и Rp (доходность портфеля).
Далее есть два способа рассчитать бета-коэффициент.
Способ №1
Для расчета коэффициента будем использовать формулы Excel «ИНДЕКС» и «ЛИНЕЙН», в значениях из таблицы выше формула примет вид:
Получаем значение бета-коэффициента, равное 1,56, что в соответствии с описанной выше интерпретацией говорит нам о том, что на данном временном промежутке акции Сбера были более волатильными, чем рыночный портфель, в качестве которого использовался индекс Московской биржи.
Способ №2
На зависимость между доходностями акции и рыночного портфеля можно смотреть как на линейную регрессию.
Уравнение простой (парной) линейной регрессии имеет следующий общий вид:
Коэффициент b1 и определяет тесноту связи переменных. Он и будет бета-коэффициентом в случае построения парной линейной регрессии для наших значений доходностей. Чтобы построить регрессию в Excel потребуется подключить в настройках пакет анализа данных.
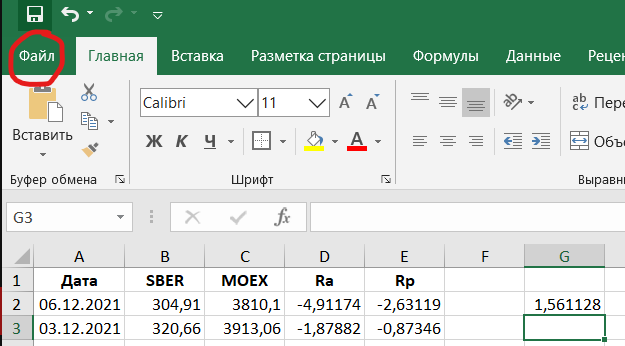
На вкладке «Файл» необходимо найти раздел «Параметры».
Он находится в левом нижнем углу.
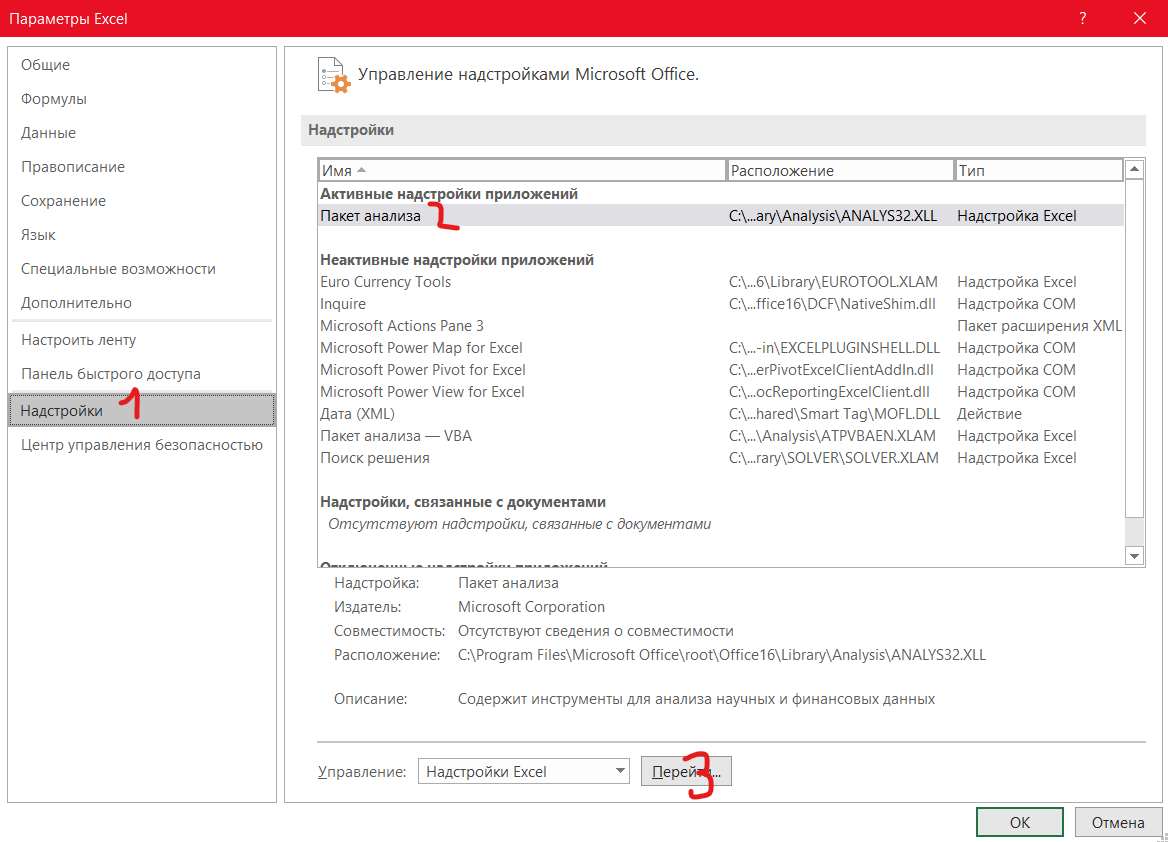
В появившемся окне переходим в раздел «Настройки» и нажимаем последовательно как на картинке:
В появившемся окне ставим галочку в поле «Пакет анализа».
Теперь пакет анализа включен и найти его можно на вкладке «Данные» в правом верхнем углу.
Далее дело за малым. Нажимаем на «Анализ данных». Выбираем в списке «Регрессия».
Заполняем входные диапазоны: Y – это значения доходностей акции, X – значения доходностей индекса (рыночного портфеля). Ставим галочку в разделе «Параметры вывода» в графе «Новый рабочий лист», нажимаем «Ок».
Открывается новый рабочий лист, на котором мы видим множество различных параметров нашей регрессии. Нас же интересует бета-коэффициент, который выделен желтым цветом.
В целом способы по своей сути одинаковые, просто во втором случае мы получаем дополнительные данные, которые будут интересны разве что тем, что хорошо разбирается в статистике. Приведенные данные позволяют оценить достоверность выявленной зависимости, статистическую значимость результата.
Бета-коэффициент можно считать для различных периодов, в зависимости от того, насколько сильно в представлении считающего менялся характер связи между акцией и индексом. Так, чем стабильнее и рынок и чем он более развит – тем больше может быть период для расчета коэффициента.
Если деятельность компании претерпела серьезные изменения, которые позволяют предположить, что степень влияния на ее деятельность рыночных рисков изменилась, не стоит принимать к расчету большой период до соответствующих изменений, так как такие значения могут исказить результат и «перевесить» более поздние и актуальные значения при расчете.