Безразмерный коэффициент
Cтраница 1
Безразмерный коэффициент ф в формуле ( 5) характеризует относительное число или вероятность участия турбулентных пульсаций потока в мелкомасштабной турбулентности.
[1]
Безразмерный коэффициент о э в этих выражениях характеризует относительное число или вероятность появления низкочастотных пульсаций в зоне горения турбулентного фронта пламени.
[2]
Безразмерный коэффициент р является одной из характеристик топлива; он зависит только от состава горючей массы топлива и не зависит от его влажности и зольности. Поэтому величины С, Н, О в формуле ( 52) могут быть написаны или без индексов, или в одинаковой мере с индексами, относящимися к горючей массе или рабочей массе топлива. В табл. 15 даны значения коэффициента Р для ряда топлив. Для твердых и жидких топлив этот коэффициент всегда положителен, для некоторых газообразных топлив он может быть отрицательным.
[3]
Безразмерный коэффициент k предлагается оценивать по одной из двух следующих формул ( см. гл.
[4]
Безразмерный коэффициент т отражает неравномерность распределения касательных напряжений по высоте поперечного сечения и зависит от его формы.
[5]
Безразмерные коэффициенты 3р и 3g здесь учитывают влияние геометрии пор и закона столкновений молекул со стенкой.
[6]
Безразмерный коэффициент зывается магнитной в им ч и вестью.
[7]
Безразмерный коэффициент / гм называется м а гни т-н о и и о с п р и и м ч и в о с т ь го.
[8]
Безразмерный коэффициент г принимается равным 1, если в радиусе 50 высот труб Я от источника перепад отметок местности не превышает 50 м на 1 км. В других случаях поправка на рельеф устанавливается на основе анализа картографического материала, освещающего рельеф местности в радиусе 50 высот труб от источника, но не менее 2 км.
[10]
Безразмерный коэффициент С подробно не расшифрован; скорее всего, это есть величина, обеспечивающая хорошее соответствие применительно к конкретной системе.
[11]
Безразмерный коэффициент v называют коэффициентом динамичности.
[12]
Безразмерный коэффициент k ( b / Ьяфф) 3 учитывает увеличение скорости и сужение потока жидкости за счет сжатия стенками колонны при подходе к сливной перегородке. Эффективная длина перегородки 6эфф практически оказывается меньше действительной длины Ъ, причем основными факторами, влияющими на се величину, оказываются расход флегмы V и относительная длина сливной перегородки С b / D. Боллес [37] рассмотрел геометрические особенности перетока флегмы через сливную перегородку и, учтя сужение потока, построил график, дающий значения поправочного коэффициента k для различных случаев. Однако Боллес использовал уравнение ( IV.
[13]
Безразмерный коэффициент называют кпзффициепгпом потерь на трение по faiute, или коэффициентом Дарси.
[14]
Безразмерные коэффициенты kltl k2i характеризуют геометрию весов.
[15]
Страницы:
1
2
3
4
|
I |
|
||||
|
0.0 |
0.2 |
0.4 |
0.6 |
1.0 |
|
|
0.5 |
1.00 |
0.91 |
0.83 |
0.74 |
0.60 |
|
1.0 |
1.00 |
0.88 |
0..77 |
0.66 |
0.50 |
|
3.0 |
1.00 |
0.82 |
0.65 |
0.50 |
0..38 |
|
5.0 |
1.00 |
0.78 |
0.57 |
0.43 |
0.35 |
|
7.0 |
1.00 |
0.74 |
0.52 |
0.39 |
0.32 |
![]()
(1.48)
где
su
– предельно допустимая средняя осадка
основания под зданием, м; sp,th
–
осадка основания под действием полезной
нагрузки, м; kfor
– то же, что и формуле (1.39);
– относительная сжимаемость мерзлых
грунтов при оттаивании, определяется
испытанием, при его отсутствии для
предварительных расчетов может быть
найдена по его физическим характеристикам,
например, по табл. 1.16.
Осадка предварительно
оттаянного основания под действием
полезной нагрузки определяется методом
эквивалентного слоя (Цытович, 1970):
![]()
(1.49)
где
![]()
–
коэффициент эквивалентного слоя,
принимается в зависимости от вида грунта
под подошвой фундамента и отношения
длины фундамента к его ширине (табл.
1.15);
![]()
–
коэффициент сжимаемости предварительно
оттаянного грунта, 1/Па; p0
– среднее дополнительное давление на
грунт под подошвой фундамента, определяется
по формуле (1.37).
Таблица
1.15
Значение
коэффициента эквивалентного слоя
.
|
Вид грунта |
Отношение длины |
|||||
|
1.0 |
1.5 |
2.0 |
3.0 |
5.0 |
10.0 |
|
|
Гравий и галька |
0.89 |
1.09 |
1.23 |
1.46 |
1.74 |
2.15 |
|
Пески |
0.94 |
1.15 |
1.30 |
1.54 |
1.84 |
2.26 |
|
Супеси и суглинки |
0.99 |
1.21 |
1.37 |
1.62 |
1.94 |
2.38 |
|
Глины |
1.24 |
1.52 |
1.72 |
2.01 |
2.42 |
2.98 |
В
случае, если основание здания представлено
неоднородными грунтами, то входящие в
расчет грунтовые показатели усредняются
с учетом толщины слоя (принимается
средневзвешенное по слоям значение).
При этом осреднение производится в
интервале глубин: для параметров Lv
и
– от Hp,th
до Hp,th
+ 3 м, для параметров f
и th
– от 0. м до Hp,th
+ 3 м, для параметра
–
от hф
до hф
+ 2.5bф.
Способ
обеспечения устойчивости путем локального
предварительного оттаивания ВМГ. Целью
расчета является определение длины
свай l, диаметра предварительно оттаянной
зоны вокруг сваи D и глубины предварительного
оттаивания Hp,th.
Расчет заимствован из нормативной
литературы (Рекомендации, 1983), где он
разработан для случая крупнообломочных
и песчаных грунтов, осадка которых
происходит практически одновременно
с оттаиванием (scon
= 0.0). Расчетная схема задачи показана
на рис. 3.24. Расчет ведется по первой и
второй группе предельных состояний в
соответствии с предельными условиями:
Таблица 1.16
Зависимость
относительной просадки грунтов при
оттаивании от льдосодержания (CТО
Газпром 2-3.1-233-2008).
|
Льдосодержание, кг/м3 |
180 |
200 |
225 |
250 |
275 |
300 |
325 |
350 |
|
Просадочность, б.р. |
0.001 |
0.002 |
0.005 |
0.008 |
0.012 |
0.015 |
0.018 |
0.022 |
|
Льдосодержание, кг/м3 |
375 |
400 |
425 |
450 |
485 |
500 |
525 |
550 |
|
Просадочность, б.р. |
0.025 |
0.029 |
0.032 |
0.035 |
0.040 |
0.073 |
0.029 |
0.184 |
|
Льдосодержание, кг/м3 |
575 |
600 |
625 |
650 |
700 |
730 |
750 |
775 |
|
Просадочность, б.р. |
0.240 |
0.296 |
0.351 |
0.407 |
0.518 |
0.584 |
0.629 |
0.685 |
|
Льдосодержание, кг/м3 |
800 |
825 |
850 |
875 |
900 |
917 |
||
|
Просадочность, б.р. |
0.740 |
0.796 |
0.851 |
0.907 |
0.962 |
1.00 |
Примечание:
Льдосодержание =
![]()
(![]()
плотность
грунта, кг/м3;
![]()
суммарная
влажность, количество незамерзшей воды,
д.е.)
F
≤ Fu
/ γn
, (1.50)
σx,a
≤
σx,p
/ γn1
, (1.51)
s
≤ su
,
(1.52)
где F
– расчетная нагрузка на сваю, Н; Fu
– несущая способность сваи, Н; σx,a
–
горизонтальная составляющая активного
напряжения в грунте (распор) на глубине
заложения острия сваи, Па; σx,p
–
горизонтальная составляющая пассивного
напряжения в грунте (отпор) на глубине
заложения острия сваи, Па; s – осадка
основания, м; su
– предельно допустимая максимальная
осадка основания, определяется по табл.
1 Приложения 5, м; γn
– коэффициент надежности, принимается
равным γn
=1.2, если несущая способность сваи
определена по результатам полевых
испытаний статической нагрузкой, γn
= 1.25, если несущая способность сваи
определена по результатам полевых
испытаний динамической нагрузкой, γn
= 1.4, если несущая способность сваи
определена расчетом;
γn1
– коэффициент надежности для горизонтальных
нагрузок, принимается равным γn1
= 1.2.
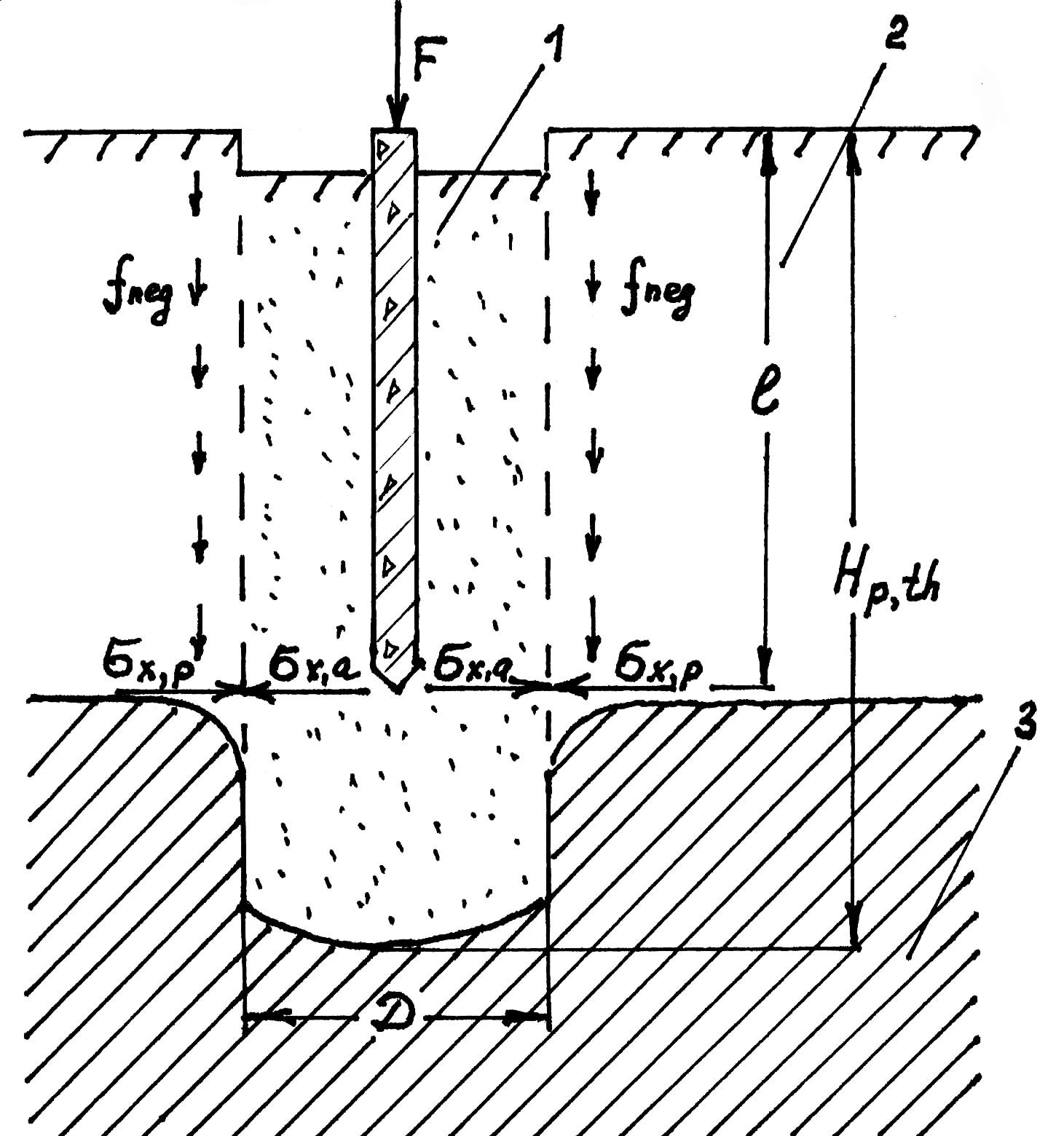
Рис.
1.22
Схема к расчету основания здания,
возводимого по способу локального
оттаивания ВМГ.
1
– предварительно оттаянный грунт; 2 –
грунт, оттаявший до окончания периода
эксплуатации здания; 3 – мерзлый грунт,
оттаивание которого произойдет при
дальнейшей эксплуатации здания.
Несущая способность
сваи определяется по формуле (СНиП
2.02.03-85):
Fu
= γcR∙R∙Aф
+![]()
(1.53)
где R
–расчетное сопротивление грунта под
нижним концом сваи, принимается по
Приложению к СНиП 2.02.04-88, Па; Аф
– площадь поперечного сечения сваи,
м2;
up
– наружный периметр поперечного сечения
сваи, м; fi
– расчетное сопротивление i-го слоя
грунта основания на боковой поверхности
сваи, принимается по Приложению к СНиП
2.02.03-85, Па; hi
– толщина i-го слоя грунта, соприкасающегося
с боковой поверхностью сваи,м; m – число
слоев грунта до глубины l (l – длина
подземной части сваи в м); γcR,
γсf
– коэффициенты условий работы грунта,
соответственно, под нижним концом и
боковой поверхностью сваи, принимаются
по табл. 1.17.
Горизонтальные
составляющие активного и пассивного
напряжения в грунте определяются по
формулам (Рекомендации, 1983):
![]()
(1.54)
![]()
(1.55)
где p
– давление на предварительно оттаянный
грунт под нижним концом сваи, вычисляемое:
p = F / (π∙D2/4),
Па; pneg
– давление за счет сил негативного
трения оттаивающего грунта,
![]()
(D – диаметр зоны предварительно
оттаянного грунта, м;
![]()
–
сила трения грунта по грунту, принимается
равной
=
0.1∙105
Па), Па; g – ускорение силы тяжести, g
=9.81 м/c2;
ρth
, ρsb
– плотность предварительно оттаянного
грунта и плотность этого же грунта во
взвешенном водой состоянии, кг/м3;
l – длина сваи, м; с – сцепление оттаянного
грунта, Па; φ – угол внутреннего трения
оттаянного грунта, град.;
![]()
– безразмерный параметр, определяемый
по табл. 1.18.
Таблица 1.17
Коэффициенты
условий работы грунта
|
Способы погружения |
γcR |
γсf |
|
Непосредственной |
1.0 |
1.0 |
|
Забивкой или |
1.0 |
0.5 |
|
Забивкой или |
1.0 |
0.6 |
|
Забивкой или |
1.0 |
1.0 |
Таблица 1.18
Значения
безразмерного параметра
|
φ,град. |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|
0.85 |
1.65 |
2.20 |
2.85 |
3.90 |
5.70 |
8.50 |
14.00 |
Осадка свай
определяется по формуле компрессионного
уплотнения грунта:
![]()
(1.56),
где
![]()
–
глубина предварительного оттаивания
грунта в месте расположения сваи,
принимается равной
=
![]()
,
где
–
то же, что и в формуле (1.38), м.
При
расчете
учитывается
ускорение оттаивания грунта в процессе
эксплуатации здания за счет наличия в
основании зон предварительно оттаянного
грунта. Это осуществляется умножением
безразмерного времени I, вычисляемого
по формуле (1.42), на безразмерный коэффициент
![]()
, вычисляемый по формуле:
![]()
(1.57)
где
np
– общее количество свай под зданием;
bзд,
lзд
– ширина и длина здания, м.
Опишем алгоритм
расчета. Вначале подбором из условия
(1.50) определяем длину сваи l, при этом
следует помнить, что она согласно
нормативным требованиям не должна быть
меньше глубины сезонного оттаивания
грунта в естественных условиях плюс 2
м. Далее подборм из условия (1.51) находим
диаметр оттаиваемой зоны D, последний
по условиям погружения сваи не может
быть меньше удвоенной величины диаметра
круглой или диагонали прямоугольной
сваи. Затем находят глубину оттаивания
грунта в месте расположения сваи,
используя формулы (1.38) – (1.42), (1.57) и
номограмму на рис. 1.20. После этого по
формуле (1.56) вычисляем осадку сваи и
проверяем условие (1.52). Если последнее
не выполняется увеличиваем длину сваи
на величину, обеспечивающую выполнение
этого условия, и расчет повторяем.
Способ
обеспечения устойчивости путем
стабилизации начального положения
верхней границы ВМГ с помощью вентилируемого
подполья. Целью
расчета является определение глубины
заложения свайного фундамента l, мощности
талого слоя Н и модуля вентиляции
подполья М (если глубина залегания
верхней границы ВМГ в естественных
условиях Н0
оказывается меньше Н, то производится
предварительное оттаивание до глубины
Н). Расчетная схема задачи показана на
рис. 1.23. Расчет ведется по первой и второй
группе предельных состояний, исходя из
условий:
![]()
,
(1.58)
![]()
,
(1.59)
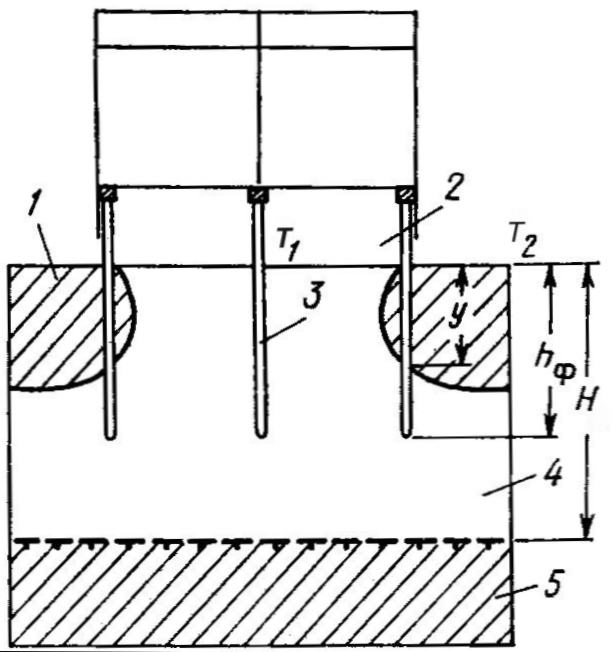
Рис.
1.23 Схема
к расчету основания здания, возводимого
по способу стабилизации с вентилируемым
подпольем.
1 – слой многолетнего
промерзания; 2 – вентилируемое подполье;
3 – фундамент; 4 –
слой талого грунта; 5 – ВМГ.
![]()
,
(1.60)
![]()
,
(1.61)
где
n1
– коэффициент перегрузки, принимаемый
равным 1.1;
![]()
–
нормативная нагрузка, передаваемая на
сваю, Н;
![]()
–
несущая способность сваи, Н;
![]()
коэффициент надежности, принимаемый
равным 1.4;
![]()
нормативное значение силы, удерживающей
сваю от выпучивания, Н;
![]()
–
коэффициент перегрузки, принимаемый
равным 0.9;
![]()
действующая
на сваю касательная сила пучения при
многолетнем промерзании грунта, Н; s –
осадка сваи, расположенной под серединой
здания, м;
![]()
предельно
допустимая максимальная осадка здания,
определяется по Приложению к СНиП
2.02.01-83, м; l – длина подземной части сваи,
м.
Несущую способность
сваи рассчитывают по формуле (1.53),
действующую на сваю силу пучения – по
формуле (1.62), силу, удерживающую сваю от
выпучивания, – по формуле (1.63):
![]()
(1.62)
![]()
(1.63)
где
![]()
периметр
сваи, м;
![]()
удельная
касательная сила пучения, принимается
по табл. 1.19, Па; y – допустимая глубина
многолетнего промерзания у края здания
в м, назначается равной y = Hf
+ 1 м (Нf
– глубина сезонного промерзания грунта
на оголенной площадке);
![]()
–
нормативное значение удельного
сопротивления сдвигу талого грунта
основания по боковой поверхности
фундамента, определяется по
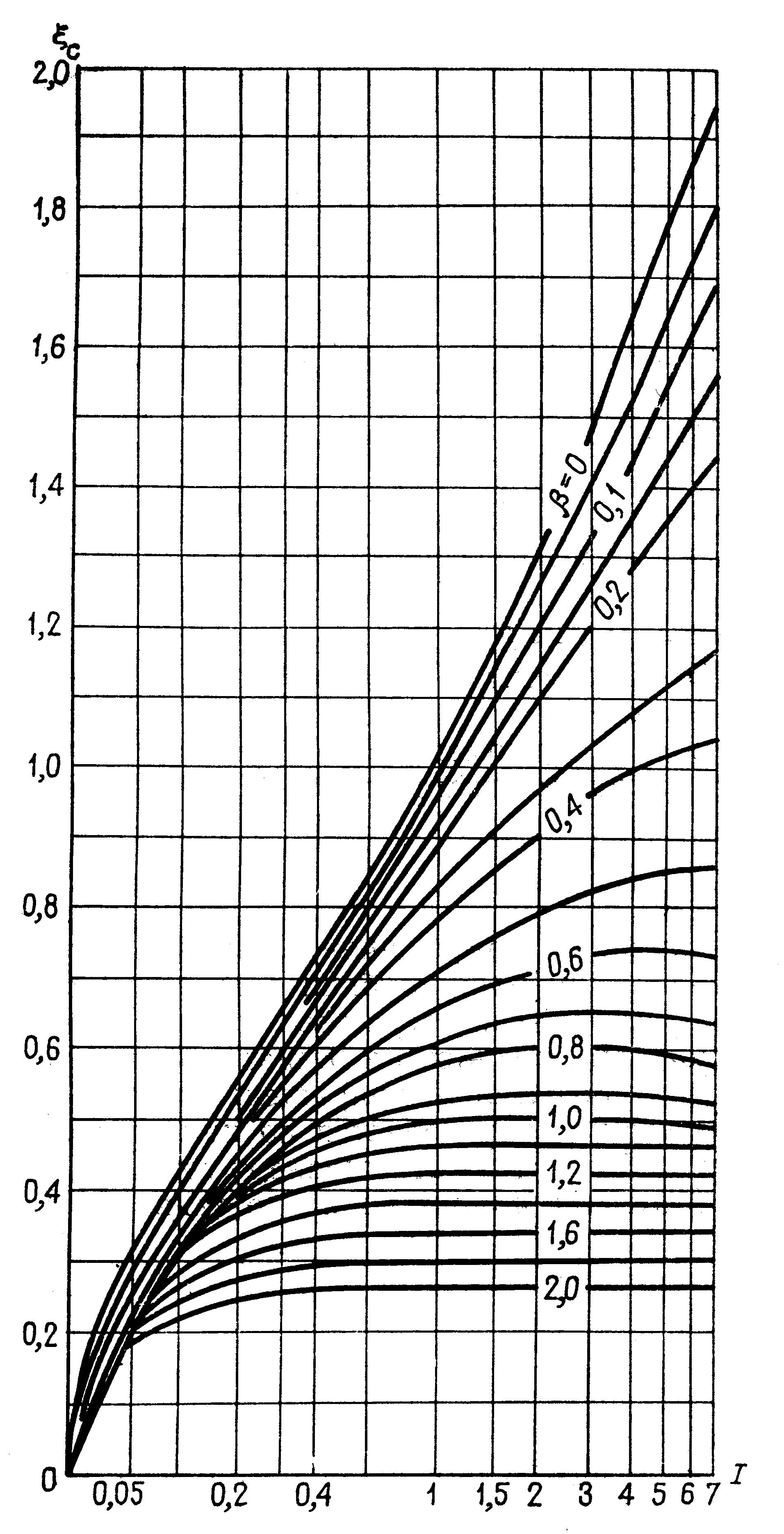
Рис.
1.24 Номограмма
для определения глубины оттаивания под
серединой здания, расположенного на
участке с ВМГ сливающегося типа.
результатам
опытных исследований, при их отсутствии
значение
для
песчаных грунтов можно принимать равным
0.3105
Па, для глинистых – 0.2105
Па.
Таблица
1.19
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Гидравлическое сопротивление
Опубликовано 24 Июн 2018
Рубрика: Теплотехника | 36 комментариев
 Выполнение расчета гидравлического сопротивления отдельного трубопровода и всей системы в комплексе является ключевой задачей в гидравлике, решение которой позволяет подобрать сечения труб и насос с необходимыми значениями давления и расхода в рабочем режиме.
Выполнение расчета гидравлического сопротивления отдельного трубопровода и всей системы в комплексе является ключевой задачей в гидравлике, решение которой позволяет подобрать сечения труб и насос с необходимыми значениями давления и расхода в рабочем режиме.
В одной из ранних статей на блоге рассмотрен простой пример расчета трубопровода с параллельными участками с использованием понятия «характеристика сопротивления». В конце статьи я анонсировал: «Можно существенно повысить точность метода…». Под этой фразой подразумевалось учесть зависимость характеристик сопротивления от расхода более точно. В том расчете характеристики сопротивлений выбирались из таблиц по диаметру трубы и по предполагаемому расходу. Полковов Вячеслав Леонидович написал взамен таблиц пользовательские функции в Excel для более точного вычисления гидравлических сопротивлений, которые любезно предоставил для печати. Термины «характеристика сопротивления» и «гидравлическое сопротивление» обозначают одно и то же.
Краткая теория.
В упомянутой выше статье теория вкратце рассматривалась. Освежим в памяти основные моменты.
Движение жидкостей по трубам и каналам сопровождается потерей давления, которая складывается из потерь на трение по длине трубопровода и потерь в местных сопротивлениях – в изгибах, отводах, сужениях, тройниках, запорной арматуре и других элементах.
В гидравлике в общем случае потери давления вычисляются по формуле Вейсбаха:
∆Р=ζ·ρ·w²/2, Па, где:
- ζ – безразмерный коэффициент местного сопротивления;
- ρ – объёмная плотность жидкости, кг/м3;
- w – скорость потока жидкости, м/с.
Если с плотностью и скоростью всё более или менее понятно, то определение коэффициентов местных сопротивлений – достаточно непростая задача!
Как было отмечено выше, в гидравлических расчетах принято разделять два вида потерь давления в сетях трубопроводов.
- В первом случае «местным сопротивлением» считается трение по длине прямого участка трубопровода. Перепад давления для потока в круглой трубе рассчитывается по формуле Дарси-Вейсбаха:
∆Ртр=ζтр·ρ·w²/2=λ·L·ρ·w²/(2·D), Па, где:
- L – длина трубы, м;
- D – внутренний диаметр трубы, м;
- λ – безразмерный коэффициент гидравлического трения (коэффициент Дарси).
Таким образом, при учете сопротивления трению коэффициент потерь – коэффициент местного сопротивления – и коэффициент гидравлического трения связаны для круглых труб зависимостью:
ζтр=λ·L/D
- Во втором случае потери давления в местных сопротивлениях вычисляются по классической формуле Вейсбаха:
∆Рм=ζм·ρ·w²/2, Па
Коэффициенты местных сопротивлений определяются для каждого вида «препятствия» по индивидуальным эмпирическим формулам, полученным из практических опытов.
Выполним ряд математических преобразований. Для начала выразим скорость потока через массовый расход жидкости:
w=G/(ρ·π·D²/4), м/с, где:
- G – расход жидкости, кг/с;
- π – число Пи.
Тогда:
∆Ртр=8·λ·L·G²/(ρ·π²·D5), Па;
∆Рм=8·ζм·G²/(ρ·π²·D4), Па.
Введем понятие гидравлических сопротивлений:
Sтр=8·λ·L·/(ρ·π²·D5), Па/(кг/с)²;
Sм=8·ζм·/(ρ·π²·D4), Па/(кг/с)².
И получим удобные простые формулы для вычисления потерь давления при прохождении жидкости в количестве G через эти гидравлические сопротивления:
∆Ртр=Sтр·G², Па;
∆Рм=Sм·G², Па.
Размерность гидравлического сопротивления (Па/(кг/с)²) определена массовой скоростью (кг/с) движения жидкости, а физические процессы в транспортных системах зависят от её объёмной скорости (м3/с), что учтено в формулах присутствием объёмной плотности ρ транспортируемой жидкости.
Для удобства последующих расчётов целесообразно введение понятия «гидравлическая проводимость» – а.
Для последовательного и параллельного соединений гидравлических сопротивлений справедливы формулы:
Sпосл=S1+S2+…+Sn, Па/(кг/с)²;
Sпар=1/(а1+a2+…+an)², Па/(кг/с)²;
ai=(1/Si)0,5, (кг/с)/Па0,5.
Коэффициент гидравлического трения.
Для определения гидравлического сопротивления от трения о стенки трубы Sтр необходимо знать параметр Дарси λ – коэффициент гидравлического трения по длине.
В технической литературе приводится значительное количество формул разных авторов, по которым выполняется вычисление коэффициента гидравлического трения в различных диапазонах значений числа Рейнольдса.

Обозначения в таблице:
- Re – число Рейнольдса;
- k – эквивалентная шероховатость внутренней стенки трубы (средняя высота выступов), м.
В [1] приведена еще одна интересная формула расчета коэффициента гидравлического трения:
λ=0,11·[(68/Re+k/D+(1904/Re)14)/(115·(1904/Re)10+1)]0,25
Вячеслав Леонидович выполнил проверочные расчеты и выявил, что вышеприведенная формула является наиболее универсальной в широком диапазоне чисел Рейнольдса!
Значения, полученные по этой формуле чрезвычайно близки значениям:
- функции λ=64/Re для зоны ламинарного характера потока в диапазоне 10<Re<1500;
- функции λ=0,11·(68/Re+k/D)0,25 для зоны турбулентного характера потока при Re>4500;
- в диапазоне 1500<Re<4500 согласно анализу присутствует переходная зона.
В переходной зоне, согласно опытам Никурадзе, график функции λ=f(Re,D,k) имеет сложную форму. Он представляет собой две сопряженные обратные кривые, которые в свою очередь сопрягаются с одной стороны с кривой гладких труб (ламинарный поток), а с другой стороны с прямыми относительной шероховатости.
Данная зона до конца не изучена, поэтому желательно гидравлические режимы проектируемых систем рассчитывать без захода в эту область: 1500<Re<4500!
На следующем рисунке показаны графики функции λ=f(Re,D,k), построенные по вышеприведенной универсальной формуле. Характер кривых в переходной области соответствует графикам Никурадзе [2, 4].

Пользовательская функция в Excel КтрТрубаВода(Рвода,tвода,G,D,kэ) выполняет расчет коэффициента гидравлического трения λ по рассмотренной универсальной формуле. При этом везде далее kэ=k.
Внимание!
- В зоне переходного характера потока происходит смена знака наклона кривой λ, что может вызвать неработоспособность систем автоматического регулирования!
- ПФ КтрТрубаВода(Pвода,tвода,G,D,kэ) при турбулентном потоке существенно зависит от значения kэ – эквивалентной шероховатости внутренней поверхности трубы. В связи с этим следует обращать внимание на задание объективного значения kэ с учётом используемых при монтаже труб (см. [2] стр.78÷83).
Для облегчения выполнения рутинных гидравлических расчетов Полковов В.Л. разработал ряд пользовательских функций. Перечень некоторых из них, наиболее часто используемых на практике, приведен в таблице ниже.

Некоторые пояснения по аргументам пользовательских функций:
- ГСдиффузор(Pвода,tвода,G,Dmin,Dmax,kэ,L) – свободные размеры;
- ГСпереходДиффузор(Pвода,tвода,G,Dmin,Dmax,kэ) – стандартный переход;
- ГСконфузор(Pвода,tвода,G,Dmin,Dmax,kэ,L) – свободные размеры;
- ГСпереходКонфузор(Pвода,tвода,G,Dmin,Dmax,kэ) – стандартный переход;
- ГСотвод(Pвода,tвода,G,D0,R0,Угол,kэ) – свободные размеры;
- ГСотводГОСТ(Pвода,tвода,G,D,Угол,kэ) – стандартный отвод.
Приведённые пользовательские функции желательно использовать с учётом начального участка транспортирования (расстояния от одного гидравлического сопротивления до следующего гидравлического сопротивления). Это позволяет уменьшить погрешности расчётов, вызванных влиянием «неустановившегося» характера потока жидкости.
Для турбулентных течений длина начального участка должна быть не менее:
Lнач=(7,88·lg (Re) – 4,35)·D
Для ламинарных течений минимальная длина начального участка:
Lнач=B·Re·D
Здесь В=0,029 по данным Буссинекса, и В=0,065 по данным Шиллера, D — внутренний диаметр системы транспортирования.



Далее на скриншоте показана таблица в Excel с примерами расчетов гидравлических сопротивлений.

Литература:
- Черникин А.В. Обобщение расчета коэффициента гидравлического сопротивления трубопроводов // Наука и технология углеводородов. М.: 1998. №1. С. 21–23.
- И.Е. Идельчик, «Справочник по гидравлическим сопротивлениям». 3-е издание, переработанное и дополненное. Москва, «Машиностроение», 1992.
- А.Д. Альтшуль, «Гидравлические сопротивления», издание второе, переработанное и дополненное. Москва, «НЕДРА», 1982.
- Б.Н. Лобаев, д.т.н., профессор, «Расчёт трубопроводов систем водяного и парового отопления». Государственное издательство литературы по строительству и архитектуре. УССР, Киев, 1956.
Ссылка на скачивание файла: gidravlicheskie-soprotivleniya (xls 502,0KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
21Июл
Пример расчёта сезонной глубины промерзания грунтов
Рассмотрим методику расчёта сезонной глубины промерзания грунта.
1.Исходные данные
Расчет выполнен в соответствии:
СП 22.13330.2011 Основания зданий и сооружений
СП 131.13330.2012 Строительная климатология
Коэффициент влияния теплового режима kh: 1.1
Для населенного пункта Москва согласно СП 131.13330.2012 Таблице 5 месяца с отрицательной среднемесячной температурой представлены ниже:
Январь t1=-7.8°C
Февраль t2=-7.1°C
Март t3=-1.3°C
Ноябрь t11=-1.1°C
Декабрь t12=-5.6°C
2.Расчёт
Определим значение Mt-безразмерного коэффициента, численного равного сумме абсолютных значений среднемесячных отрицательных температур согласно п.5.5.3 СП 22.13330.2011.
Mt=(7.8+7.1+1.3+1.1+5.6)=22.9
Вид грунтов: Супеси,пески мелкие и пылеватые
Тогда значение нормативной глубины сезонного промерзание грунтов определим по формуле (5.3 СП 22.13330.2011) dfn=d0(Mt)0.5
где d0-величина принимаемая для вида грунта -супеси,пески мелкие и пылеватые равной 0.28м в соответствии с указаниями п.5.5.3 СП 22.13330.2011.
Тогда
dfn=0.28(22.9)0.5=1.34м
Расчетную глубину промерзания грунта определим по формуле (5.4 СП 22.13330.2011)
df=dfnkh=1.34·1.1=1.47м
Вид грунтов: Суглинки и глины
Тогда значение нормативной глубины сезонного промерзание грунтов определим по формуле (5.3 СП 22.13330.2011) dfn=d0(Mt)0.5
где d0-величина принимаемая для вида грунта -суглинки и глины равной 0.23м в соответствии с указаниями п.5.5.3 СП 22.13330.2011.
Тогда
dfn=0.23(22.9)0.5=1.1м
Расчетную глубину промерзания грунта определим по формуле (5.4 СП 22.13330.2011)
df=dfnkh=1.1·1.1=1.21м
Вид грунтов: Пески гравелистые,крупные и средней крупности
Тогда значение нормативной глубины сезонного промерзание грунтов определим по формуле (5.3 СП 22.13330.2011) dfn=d0(Mt)0.5
где d0-величина принимаемая для вида грунта -пески гравелистые,крупные и средней крупности равной 0.3м в соответствии с указаниями п.5.5.3 СП 22.13330.2011.
Тогда
dfn=0.3(22.9)0.5=1.44м
Расчетную глубину промерзания грунта определим по формуле (5.4 СП 22.13330.2011)
df=dfnkh=1.44·1.1=1.58м
Вид грунтов: Крупнообломочные грунты
Тогда значение нормативной глубины сезонного промерзание грунтов определим по формуле (5.3 СП 22.13330.2011) dfn=d0(Mt)0.5
где d0-величина принимаемая для вида грунта -крупнообломочные грунты равной 0.34м в соответствии с указаниями п.5.5.3 СП 22.13330.2011.
Тогда
dfn=0.34(22.9)0.5=1.63м
Расчетную глубину промерзания грунта определим по формуле (5.4 СП 22.13330.2011)
df=dfnkh=1.63·1.1=1.79м
Таблицу глубин промерзания разных типов грунта по регионам и населённым пунктам России можно посмотреть здесь.
круглым устоем достигается при неблагоприятных метеорологических
условиях на расстоянии Хм, м, от источника и
определяется по формуле
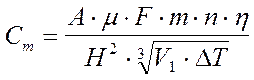
где А — коэффициент,
зависящий от температурной стратификации атмосферы (для европейской территории
СНГ — 160);
m — масса вредного вещества, выбрасываемого в атмосферу
в
единицу времени, г/с;
F —
безразмерный коэффициент, учитывающий скорость оседания вредных веществ в
атмосферном воздухе;
n, m —
коэффициенты учитывающие условия выхода газовоздушной смеси
из устья источника выброса;
H – высота
источника выброса над уровнем земли, м;
h – безразмерный
коэффициент, учитывающий влияние рельефа местности, в случае ровной или слабопересеченной местности;
DT – разность между температурой
выбрасываемой воздушной смеси ТГ и температурой
окружающего атмосферного воздуха ТВ, 0С;
V1 – расход газовоздушной смеси,
м3/с.
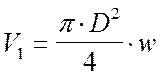
где D – диаметр устья источника выброса, м;
w – средняя скорость выхода газовоздушной
смеси из устья источника выброса, м3/с.
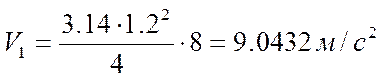
Значение безразмерного коэффициента F
принимаем равным:
1.0 – для сероводорода;
1.0 – для сернистого ангидрида.
Значение коэффициентов m
и n. определяются
в зависимости от параметров
f,
Vм:
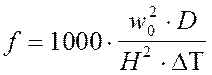
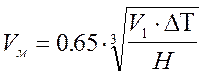
Находим значение коэффициентов f, Vм:
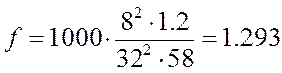
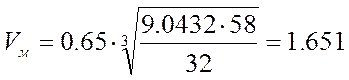
Для 0.5<Vм<2 n рассчитаем по формуле:
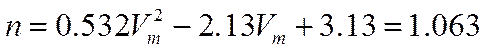 ;
;
Коэффициент m при f<100
вычисляется по формуле
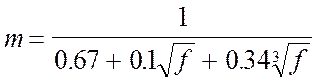
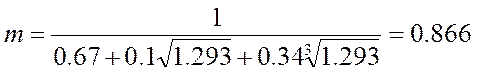 ;
;
Определяем значение максимальной концентрации:
для сероводорода
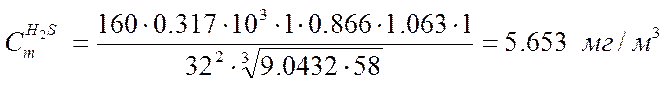
для сернистого ангидрида
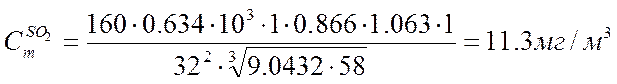
2. РАСЧЕТ РАССТОЯНИЯ, НА КОТОРОМ ДОСТИГАЕТСЯ
МАКСИМАЛЬНАЯ КОНЦЕНТРАЦИЯ
Расстояния
Хм, от источника выброса, на котором приземная
концентрация С мг/м3, при
неблагоприятных метеорологических условиях достигает максимального значения и
определяется по формуле
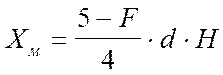
где
d – безразмерный коэффициент, который при f < 100 и 0.5<Vм<2 определяется по формуле
![]()
![]()
![]()
Определяем расстояние Хм для окиси углерода и сернистого ангидрида
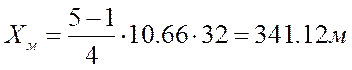
Значение опасной скорости UМ, м/с, на уровне флюгера, при которой достигается
наибольшее значение приземной концентрации вредных веществ См, в
случае f < 100 и 0.5£Vм<2:
![]()
3. ИЗМЕНЕНИЕ МАКСИМАЛЬНОЙ
КОНЦЕНТРАЦИИ И
РАСССТОЯНИЯ. НА КОТОРОМ ОНА ДОСТИГАЕТСЯ
ПРИ СКОРОСТИ ВЕТРА,
ОТЛИЧНОЙ ОТ ОПАСНОЙ
Максимальные значения приземной
концентрации С, мг/м3, при
неблагоприятных метеорологических условиях и скорости ветра U,
м/с, отличающейся от опасной скорости ветра UM, м/с, определяется по формуле:
![]()
где r – безразмерная
величина, определяемая в зависимости от отношения U/UM.
При U/UM £1
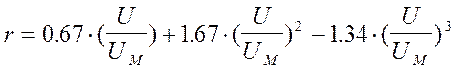
При
U/UM > 1
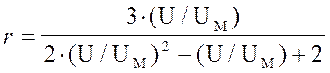
Расчет приведен в таблице:
|
U м/с |
U/Um |
r |
С’ мг/м3 |
С’’ мг/м3 |
С’/ПДК |
C’’/ПДК |
|
1 |
0.6 |
0.713 |
4.03 |
8.057 |
503.75 |
161.14 |
|
1.651 |
1 |
1 |
5.653 |
11.3 |
706.625 |
226 |
|
3 |
1.817 |
0.803 |
4.539 |
9.074 |
567.45 |
181.48 |
Расстояние
от источника выброса Х, м, на котором при скорости ветра U,
м/с, и неблагоприятных метеорологических условиях приземная концентрация
вредных веществ достигает максимального значения СМН, мг/м3,
определяется по формуле:
![]()
где
p — безразмерный коэффициент, определяемый в
зависимости от отношения U/UM:
При U/UM £ 0,25
![]()
При 0,25 < U/UM £ 1
![]()
При
U/UM > 1
![]()
Расчеты приведены в таблице:
|
U м/с |
U/Um |
P |
XmU |
|
1 |
0.6 |
1.086 |
370.456 |
|
1.651 |
1 |
1 |
341.12 |
|
3 |
1.817 |
1.261 |
430.152 |
4. РАСЧЕТ КОНЦЕНТРАЦИИ ЗАГРЯЗНЯЮЩИХ ВЕЩЕСТВ НА
РАЗЛИЧНЫХ РАССТОЯНИЯХ ОТ ИСТОЧНИКА
При опасной скорости nм приземная концентрация вредных веществ, С, мг/м3, в атмосфере по оси
факела на различных расстояниях Х, м, от источника выброса
определяется по формуле
![]()
где
– безразмерный коэффициент, определяемый в зависимости
от отношения Х / Хм и
коэффициента F.
Коэффициент S1 на расстоянии Х
= 50 м от источника выброса имеет значение Х / Хм = 0.146.
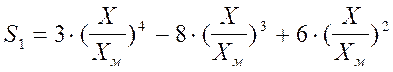
![]()
![]()
![]()
Для других значений Х и С результаты расчетов ведем по
формулам
При X/XM
£ 1
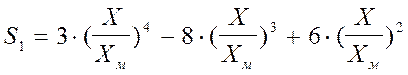
При 1< X/XM £ 8
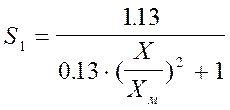
При X/XM
> 8
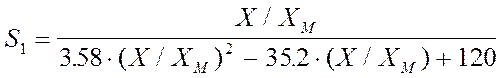
Все расчеты приведем в табличной форме:
где С’ — CH2S,
C’’ — CSO2.
|
X |
X/Xm |
S1 |
C’мг/м3 |
C’’мг/м3 |
C’/ПДК |
C’’/ПДК |
|
50 |
0.146 |
0.104 |
0.588 |
1.175 |
73.5 |
23.5 |
|
100 |
0.293 |
0.335 |
19 |
3.8 |
237.5 |
76.08 |
|
150 |
0.439 |
0.59 |
33.3 |
6.66 |
416.25 |
133.2 |
|
200 |
0.586 |
0.8 |
45.2 |
9.04 |
565.05 |
180.8 |
|
250 |
0.732 |
0.938 |
53 |
10.6 |
662.5 |
212.06 |
|
300 |
0.879 |
0.993 |
56.1 |
11.22 |
701.28 |
224.4 |
|
500 |
1.465 |
0.883 |
49.94 |
9.983 |
624.25 |
199.6 |
|
1000 |
2.931 |
0.533 |
30.17 |
6.022 |
377.21 |
120.4 |
|
1500 |
4.397 |
0.321 |
18.18 |
3.627 |
227.27 |
72.5 |
|
1700 |
4.983 |
0.267 |
15.1 |
3.02 |
188.85 |
60.4 |
|
2000 |
5.863 |
0.206 |
11.68 |
2.33 |
146 |
46.69 |
|
2500 |
7.328 |
0.141 |
8 |
1.599 |
100.08 |
31.99 |
|
3000 |
8.794 |
0.1 |
5.69 |
1.138 |
71.17 |
22.76 |
РАСЧЕТ
САНИТАРНО-ЗАЩИТНОЙ ЗОНЫ
Размер
санитарно-защитной зоны:
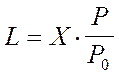
где P0 = 12.5%, а P, %, задано в
таблице:
|
С |
СВ |
В |
ЮВ |
Ю |
ЮЗ |
З |
СЗ |
|
14 |
11 |
8 |
6 |
10 |
12 |
19 |
20 |
|
X |
С |
СВ |
В |
ЮВ |
Ю |
ЮЗ |
З |
СЗ |
|
341.12 |
382.05 |
300.18 |
218.31 |
163.73 |
272.89 |
329.47 |
518.5 |
545.79 |
|
1000 |
1120 |
880 |
640 |
480 |
800 |
960 |
1520 |
1600 |
|
2000 |
2240 |
1760 |
1280 |
960 |
1600 |
1920 |
3040 |
3200 |
|
3000 |
3360 |
2640 |
1920 |
1440 |
2400 |
2880 |
4560 |
4800 |
5. РАСЧЕТ КОНЦЕНТРАЦИИ ЗАГРЯЗНЯЮЩИХ ВЕЩЕСТВ
НА РАЗЛИЧНОЙ ВЫСОТЕ ОТ
ПОВЕРХНОСТИ ЗЕМЛИ
Расчет концентраций Су,
мг/м3, на расстоянии у, м по
перпендикуляру к оси факела определяется по формуле
![]()
Коэффициент S2 определяем по формуле
![]()
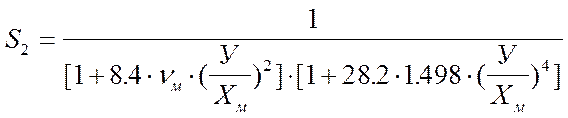
Для значений У и С результаты расчетов
сводим в таблицу,
где С’ — CH2S,
C’’ — CSO2.
|
Y |
Y/Xm |
S2 |
C’мг/м3 |
C’’мг/м3 |
C’/ПДК |
C’’/ПДК |
|
25 |
0.073 |
0.929 |
5.251 |
10.497 |
656.4 |
209.95 |
|
35 |
0.102 |
0.869 |
4.912 |
9.819 |
614 |
196.39 |
|
45 |
0.132 |
0.794 |
4.488 |
8.972 |
561 |
179.44 |
|
55 |
0.161 |
0.713 |
4.03 |
8.056 |
503.82 |
161.13 |
|
75 |
0.219 |
0.542 |
3.063 |
6.124 |
382.99 |
122.49 |
|
85 |
0.249 |
0.456 |
2.577 |
5.152 |
322.22 |
103 |
|
100 |
0.293 |
0.339 |
1.916 |
3.774 |
239.54 |
75.48 |
|
120 |
0.351 |
0.216 |
1.221 |
2.44 |
152.63 |
48.81 |
|
150 |
0.434 |
0.99 |
0.559 |
1.118 |
69.95 |
22.37 |
6. РАСЧЕТ ПРЕДЕЛЬНО ДОПУСТИМЫХ ВЫБРОСОВ
В АТМОСФЕРУ
Значение ПДВ, г/с, для
одиночного источника с круглым устьем в случае Сф <
ПДК определяется по формуле:
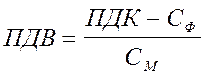
где
Сф – фоновые концентрации, составляющие 10% ого ПДК:
![]()
![]()
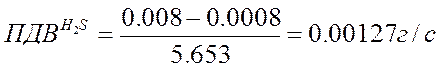
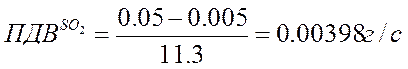
7.
РАСЧЕТ ЭКОНОМИЧЕСКОГО УЩЕРБА ОТ
ЗАГРЯЗНЕНИЯ АТМОСФЕРЫ
Экономический ущерб, руб./год, причиняемый
промышленными выбросами загрязняющих веществ в атмосферный воздух любого
источника, определяется по формуле:
![]()
где g – константа, численное значение которой принимается равным 2.4
(в ценах 1991 г);
s – показатель относительной опасности загрязнения;
f – поправка на
характер рассеивания примеси в атмосфере;
M – приведенная
масса годового выброса из источника, усл. т/год, загрязняющего вещества.
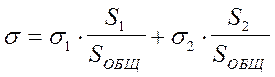
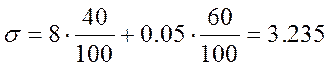
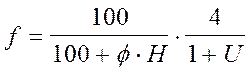
где
U — среднегодовое значение скорости ветра на уровне
флюгера
