Чтобы понять значение вероятности в инвестиционном контексте, нам необходимо различать два типа вероятности: безусловную и условную.
Как безусловные, так и условные вероятности удовлетворяют приведенному ранее определению вероятности, но они рассчитываются или оцениваются по-разному и имеют разные интерпретации. Они дают ответы на разные вопросы.
Вероятность в ответе на простой вопрос «Какова вероятность этого события (A)?» – это безусловная вероятность (англ. ‘unconditional probability’ или ‘marginal probability’), обозначаемая (P(A)).
При анализе вероятностей, представленных в таблицах, безусловные вероятности обычно выводятся в конце или на полях таблицы, отсюда и термин marginal probability, от англ. ‘margin’ – поле страницы.
Из-за возможной путаницы с тем, что термин margin используется в экономике в другом смысле (например, как маржинальный применительно к прибыли), лучше использовать термин ‘unconditional probability’.
Что такое безусловная вероятность?
Рассмотрим вопрос: «Какова вероятность того, что акция принесет доход выше безрисковой ставки (событие (A))»?
Ответ – это безусловная вероятность, которую можно рассматривать как соотношение двух величин.
Числитель – это сумма вероятностей доходности акций выше безрисковой ставки. Предположим, что эта сумма 0.70. Знаменатель равен 1, т.е. сумме вероятностей всех возможных ставок доходности.
Ответ на вопрос:
(P(A) = 0.70)
Что такое условная вероятность?
Сравните вопрос «Какова вероятность события (A)?» с вопросом «Какова вероятность события (A), учитывая, что событие (B) произошло?»
Вероятность в ответе на этот последний вопрос является условной вероятностью (англ. ‘conditional probability’), обозначаемой как ( P(A|B) ) (читается как: «вероятность (A) при условии (B)»).
Предположим, мы хотим знать вероятность того, что акция принесет доход выше безрисковой ставки (событие (A)), при условии, что акция принесет положительный доход (событие (B)). Фразой «при условии» мы ограничиваем исход доходностью более 0%.
Условная вероятность рассчитывается как отношение двух величин.
Числитель – это сумма вероятностей доходности акций выше безрисковой ставки; в данном конкретном случае числитель такой же, как и в случае с безусловной вероятностью: 0.70.
Знаменатель, однако, изменяется от 1 до суммы вероятностей для всех исходов (ставок доходности) выше 0%.
Предположим, что знаменатель равен 0.80, что больше, чем 0.70, поскольку доходность от 0 до безрисковой ставки имеет некоторую положительную вероятность возникновения.
Тогда,
( P(A | B) = 0.70/0.80 = 0.875 )
Если мы наблюдаем, что акция приносит положительный доход, то вероятность доходности выше безрисковой ставки будет больше, чем безусловная вероятность, то есть вероятность события, не сопровождаемая никакой другой информацией. Результат интуитивно понятен.
В этом примере условная вероятность больше, чем безусловная вероятность. Тем не менее, в зависимости от фактов условная вероятность события может быть больше, равна или меньше безусловной вероятности.
Например, вероятность того, что акция принесет доход выше безрисковой ставки, при условии того, что акция принесет отрицательный доход, равна 0.
Уточним еще раз:
- Безусловная вероятность – это вероятность события без каких-либо ограничений; она может даже рассматриваться как отдельная вероятность.
- Условная вероятность, напротив, является вероятностью события, с учетом того, что произошло другое событие.
При обсуждении подходов к расчету вероятности мы дали одну эмпирическую оценку вероятности того, что изменение дивидендов является уменьшением дивидендов. Эта вероятность была безусловной вероятностью.
Учитывая дополнительную информацию о характеристиках компании, может ли инвестор уточнить эту оценку?
Инвесторы постоянно ищут информационное преимущество, которое поможет улучшить их прогнозы. С математической точки зрения они пытаются сформулировать свое видение будущего, используя вероятности, обусловленные соответствующей информацией или событиями. Инвесторы не игнорируют полезную информацию; они корректируют свои вероятности, чтобы учесть ее.
Таким образом, концепции условной вероятности, а также связанные с ними концепции, обсуждаемые далее, чрезвычайно важны в инвестиционном анализе и анализе финансовых рынков.
Что такое совместная вероятность?
Чтобы сформулировать точное определение условной вероятности, нам сначала нужно ввести понятие совместной вероятности (англ. ‘joint probability’).
Предположим, мы задаем вопрос: «Какова вероятность того, что произойдет и событие (A), и событие (B)?». Ответом на этот вопрос является совместная вероятность, обозначаемая ( P(AB) ) (читается как: «вероятность событий (A) и (B)»).
Если мы думаем о вероятности (A) и вероятности (B) как о наборах данных, построенных из результатов одной или нескольких случайных величин, совместная вероятность (A) и (B) является суммой вероятностей общих для них результатов.
Например, рассмотрим два события:
- акция приносит доход выше безрисковой ставки ((A)), а
- акция приносит положительный доход ((B)).
Результаты (A) содержатся в подмножестве результатов (B), поэтому (P(AB))) равно (P(A)).
Теперь мы можем сформулировать формальное определение условной вероятности, которое обеспечивает формулу для ее вычисления.
Определение условной вероятности.
Условная вероятность (A) при условии события (B) равна общей вероятности (A) и (B), деленной на вероятность (B) (предполагается, что она не равна 0).
( large P(A|B) = P(AB)/P(B), P(B) neq 0 ) (Формула 1)
Иногда мы знаем условную вероятность (P (A|B)) и хотим знать общую вероятность (P(AB)). Мы можем получить общую вероятность из следующего правила умножения для вероятностей, которое выведено из Формулы 1.
Правило умножения для вероятности.
Совместная вероятность (A) и (B) может быть выражена как:
( large P(AB) = P(A|B)P(B) ) (Формула 2)
Пример (2). Условная вероятность и предсказуемость финансовых результатов взаимного фонда.
Французский исследователь Vidal-Garcia (2013) изучил, прогнозируют ли исторические показатели будущие результаты для выборки взаимных фондов, включающей 1050 активно управляемых фондов акций в 6 европейских странах в период с 1988 по 2010 год.
Фонды были классифицированы по 9 инвестиционным стилям на основе сочетаний инвестиционной направленности (рост, смешивание и стоимость) и рыночной капитализации фонда (малая, средняя и большая капитализация).
Один из подходов, использованных Vidal-Garcia, заключался в расчете годовой доходности, скорректированной по контрольным показателям каждого фонда, путем вычитания контрольной доходности из годовой доходности фонда.
В качестве ориентиров использовались индексы стиля MSCI (Morgan Stanley Capital International).
Для каждого инвестиционного стиля фонда в каждой стране фонды классифицировались как выигрышные или проигрышные в течение каждого из двух последовательных лет.
Первые 50% фондов по доходности, скорректированной по контрольным показателям, за данный год были названы выигрышными; остальные 50% были названы проигрышными.
Выдержка из результатов исследования для 135 французских фондов, классифицируемых как крупные фонды, приведена в Таблице 2. Она показывает процентную долю тех фондов, которые были выигрышными в течение 2 лет подряд, выигрышными в течение 1 года, а также сначала проигрышными, а затем выигрышными, и проигрышными в оба года.
Например, ячейка таблицы Выигрышный (год 2) / Выигрышный (год 1) показывает, что 65,5% фондов, выигрышных в 1-м году, также были выигрышными во 2-м году. Обратите внимание, что четыре значения в таблице можно рассматривать как условные вероятности.
|
Выигрышный |
Проигрышный |
|
|---|---|---|
|
Выигрышный (год 1) |
65.5% |
34.5% |
|
Проигрышный (год 1) |
15.5% |
84.5% |
Источник: Vidal-Garcia (2013).
На основании данных Таблицы 2 сделайте следующее:
- Укажите четыре события, необходимые для определения четырех условных вероятностей.
- Сформулируйте четыре значения таблицы как условные вероятности, используя форму P(событие | событие) = значение.
- Определите, являются ли условные вероятности в части 2 эмпирическими, априорными или субъективными вероятностями?
- Используя информацию, приведенную в таблице, рассчитайте вероятность того, что фонд потерпел неудачу как в 1-м, так и в 2-м годах. (Обратите внимание, что, поскольку 50% фондов классифицируются как проигрышные в каждом году, безусловная вероятность того, что фонд будет классифицирован как проигрышный в любом году составляет 0.5).
Решение для части 1:
Четыре события, необходимые для определения условных вероятностей:
- Фонд – выигрышный в 1 году
- Фонд – проигрышный в 1 году
- Фонд – проигрышный во 2 году
- Фонд – выигрышный во 2 году
Решение для части 2:
Из ряда 1:
- P(Фонд – выигрышный во 2 году | Фонд – выигрышный в 1 году) = 0.655
- P(Фонд – проигрышный во 2 году | Фонд – выигрышный в 1 году) = 0.345
Из ряда 2:
- P(Фонд – выигрышный во 2 году | Фонд – проигрышный в 1 году) = 0.155
- P(Фонд – проигрышный во 2 году | Фонд – проигрышный в 1 году) = 0.845
Решение для части 3:
Эти вероятности рассчитываются на основе данных, поэтому они являются эмпирическими вероятностями.
Решение для части 4:
Расчетная вероятность составляет 0.423.
Если событие А означает, что фонд является проигрышным во 2-м года, а событие В – то, что фонд является проигрышным в 1-м года, то событие AB означает, что фонд является проигравшим как в 1-м, так и в 2-м году.
Берем соответствующие значения из Таблицы 2:
( P(A|B) = 0.845) и (P(B) = 0.50)
Таким образом, используя Формулу 2, мы находим:
( P(AB) = P(A|B)P(B) = 0.845(0.50) = 0.4225)
или вероятность приблизительно равную 0.423.
Формула 2 гласит, что совместная вероятность событий (A) и (B) равна вероятности (A), при условии (B), умноженной на вероятность (B).
Поскольку ( P(AB) = P(BA) ), выражение ( P(AB) = P(BA) = P(B|A)P(A) ) эквивалентно Формуле 2.
Когда у нас есть два события, (A) и (B) , которые нас интересуют, мы часто хотим знать вероятность того, что произойдет (A) или (B) . Здесь слово «или» является включающим, что означает, что происходит либо (A), либо (B) , либо (A) и (B) .
Иными словами, вероятность (A) или (B) – это вероятность того, что произойдет хотя бы одно из двух событий. Такие вероятности рассчитывается с использованием правила сложения для вероятностей.
Правило сложения для вероятностей.
При данных событиях (A) и (B) вероятность того, что произойдет (A) или (B) , или что произойдут оба события, равна вероятности того, что произойдет событие (A), плюс вероятность того, что произойдет событие (B) , минус вероятность того, что произойдут (A) и (B) .
( large P(A small{text{ или }} large B) = P(A) + P(B) – P(AB) ) (Формула 3)
Если мы рассматриваем отдельные вероятности (A) и (B) как наборы данных, построенные из результатов одной или нескольких случайных величин, первый шаг в вычислении вероятности (A) или (B) состоит в суммировании вероятностей результатов (A) для получения (P(A)).
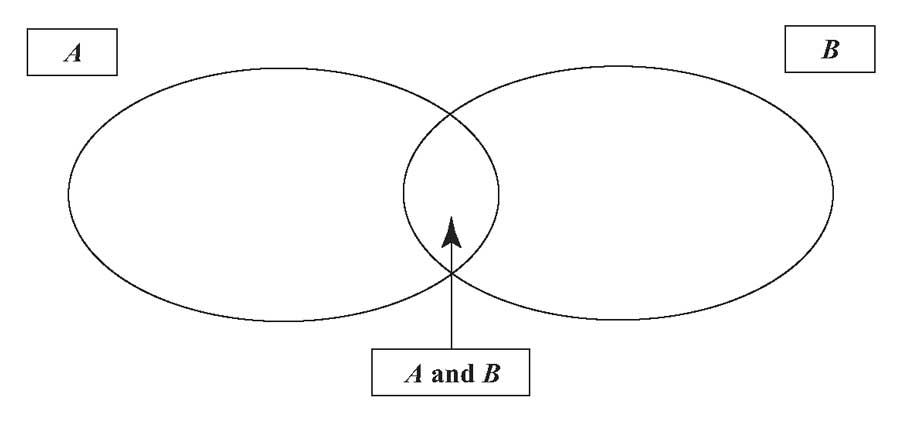
Если (A) и (B) имеют какие-либо общие результаты, то, если бы мы теперь добавили (P(B)) к (P(A)), мы бы посчитали вдвое больше вероятностей этих общих результатов. Таким образом, мы добавляем к (P(A)) величину ([P(B) – P(AB)]), которая является вероятностью результатов (B) за вычетом вероятности любых результатов, уже подсчитанных при вычислении (P(A)).
Рисунок 1 иллюстрирует этот процесс; мы избегаем двойного подсчета результатов на пересечении (A) и (B) , вычитая P(AB).
В качестве примера расчета,
если ( P(A) = 0.50, P(B) = 0.40), и (P(AB) = 0.20),
то ( P(A text{ или } B) = 0.50 + 0.40 – 0.20 = 0.70).
Только в случае если два события (A) и (B) являются взаимоисключающими, ( P(AB) ) будет равно 0.
Было бы правильно заявить, что ( P(A text{ или } B) = P(A) + P(B) ).
Следующий пример показывает, сколько полезной информации можно получить, используя несколько правил вероятности, представленных на данный момент.
Пример (3) вероятности выполнения заявки на покупку акций с ограничением цены.
У вас есть две неисполненных лимитных заявки на одну и ту же акцию.
Лимитная заявка на покупку акций по заявленной цене (или заявка с ограничением цены, от англ. ‘limit order’) – это заявка на покупку по указанной цене или ниже.
Ряд поставщиков, в том числе используемая вами интернет-служба, предоставляют предполагаемую вероятность того, что лимитная заявка будет исполнена в течение установленного периода времени, с учетом текущей цены акций и лимита цены.
Одна лимитная заявка (Заявка 2) была размещена по цене $10. Вероятность того, что она будет исполнена в течение одного часа, составляет 0.35.
Вторая лимитная заявка (Заявка 2) была размещена по цене $9.75; вероятность ее исполнения в течение одного часа составляет 0.25.
- Какова вероятность того, что Заявка 1 или Заявка 2 будут исполнены?
- Какова вероятность того, что Заявка 2 будет исполнена, при условии, что Заявка 1 также будет исполнена?
Решение для части 1:
Вероятность составляет 0.35.
Даны две вероятности: Р(Заявка 1 исполнена) = 0.35 и Р(Заявка 2 исполнене) = 0.25.
Обратите внимание, что если Заявка 2 исполнена, то, несомненно, что Заявка 1 также исполнена, потому что цена должна превысить $10, что больше $9.75.
Таким образом,
Р(Заявка 1 исполнена | Заявка 2 исполнена) = 1
а также,
Р(Заявка 1 исполнена И Заявка 2 исполнена) =
Р(Заявка 1 исполнена | Заявка 2 исполнена)
(times) P(Заявка 2 исполнена) =
= 1(0.25) = 0.25
Чтобы ответить на вопрос, мы используем правило сложения для вероятностей:
Р(Заявка 1 исполнена ИЛИ Заявка 2 исполнена) =
Р(Заявка 1 исполнена) + Р(Заявка 2 исполнена) – Р(Заявка 1 исполнена И Заявка 2 исполнена) =
= 0.35 + 0.25 – 0.25 = 0.35
Обратите внимание, что результаты, для которых Заявка 2 исполнена, являются подмножеством результатов, для которых исполнена Заявка 1.
Если вы посчитаете вероятность того, что Заявка 1 исполнена, то также посчитаете вероятность того, что исполнена Заявка 2.
Следовательно, вероятностью того, что Заявка 1 исполнена, будет 0.35.
Решение для части 2:
Если Заявка 1 исполняется, вероятность исполнения Заявки 2 составляет 0.714.
В решении для части 1 вы обнаружили, что Р(Заявка 1 исполнена И Заявка 2 исполнена) = 1(0.25) = 0.25.
Эквивалентный способ выразить эту совместную вероятность будет полезен и здесь:
Р(Заявка 1 исполнена И Заявка 2 исполнена) = 0.25 = Р(Заявка 2 исполнена | Заявка 1 исполнена) (times) P(Заявка 1 исполнена)
Поскольку известно, что P(Заявка 1 исполнена) = 0.35, у вас есть одно уравнение с одним неизвестным:
0.25 = Р(Заявка 2 исполнена | Заявка 1 исполнена) (0.35)
Вы определяете, что
Р(Заявка 2 исполнена | Заявка 1 исполнена) = 0.25/0.35 = 5/7 или примерно 0.714.
Вы также можете использовать Формулу 1, чтобы такое же решение.
Безусловная вероятность, также известная как предельная вероятность, относится к вероятности, на которую не влияют предыдущие или будущие события. Другими словами, безусловная вероятность – это вероятность события независимо от предшествующего или будущего возникновения других событий. Проще говоря, безусловная вероятность – это просто вероятность наступления события.
Резюме:
- Безусловная вероятность относится к вероятности, на которую не влияют предыдущие или будущие события.
- Безусловная вероятность события «А» обозначается как P (A).
- Условная вероятность, в отличие от безусловной вероятности, – это вероятность события, на которое может повлиять другое событие.
Формула безусловной вероятности
Следовательно, безусловная вероятность того, что событие произойдет, – это просто вероятность самого события. Безусловная вероятность не имеет условия.
Например, вероятность завтрашнего дождя сама по себе является безусловной вероятностью.
Дополнительные примеры безусловных вероятностей:
- Какова вероятность того, что на кубике выпадет 6?
- Какова вероятность выпадения головы при подбрасывании монеты?
- Какова вероятность выпадения туза пик в колоде карт?
Безусловная вероятность против условной вероятности
Условная вероятность Условная вероятность Условная вероятность – это вероятность наступления события при условии, что другое событие уже произошло. Эта концепция является одной из наиболее существенных, в отличие от безусловной вероятности, это вероятность события, которое может повлиять на другое событие или на него повлияет другое событие. Другими словами, условная вероятность, как следует из названия, сопровождается условием.
Например, вспомните следующую безусловную вероятность: «Какова вероятность дождя завтра?» Условную вероятность можно сформулировать следующим образом: «Какова вероятность дождя завтра, если сегодня солнечно?»
Дополнительные примеры условных вероятностей:
- Какова вероятность выпадения 6 и 4?
- Какова вероятность того, что сегодня солнечно, если завтра пойдет дождь?
- Какова вероятность индекса S&P 500? Секторы S&P Секторы S&P представляют собой метод сортировки публично торгуемых компаний по 11 секторам и 24 отраслевым группам. Созданные Standard & Poor’s (S&P) и Morgan Stanely Capital International (MSCI), они также известны как Глобальный стандарт отраслевой классификации (GICS). достичь рекордных максимумов, а затем закрепиться на отметке 3000?
Пример безусловной вероятности
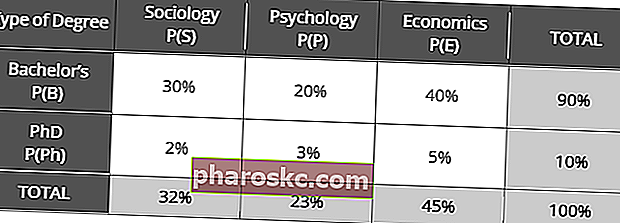
В следующей совместной таблице вероятностей показано распределение студентов, изучающих общественные науки со степенью бакалавра и доктора философии. программы:
Используя свое понимание безусловной вероятности, определите:
- Безусловная вероятность случайного выбора студента, обучающегося на степень бакалавра;
- Безусловная вероятность случайного выбора студента, изучающего социологию;
- Безусловная вероятность случайного выбора студента, изучающего докторскую степень; а также
- Безусловная вероятность случайного выбора студента, изучающего экономику.
Ответы:
- P (B) = 90%
- P (S) = 10%
- P (Ph) = 10%
- P (E) = 45%
Безусловная вероятность в новостях
Безусловную вероятность часто можно найти в новостях. Например, согласно статье CNBC, инструмент FedWatch CME Group показал трейдерам 100% вероятность снижения процентной ставки в июле 2019 года. Это само по себе является примером безусловной вероятности.
Дополнительные ресурсы
Финансы предлагают сертификацию финансового моделирования и оценки (FMVA) ™. Сертификация FMVA®. Присоединяйтесь к более 350 600 студентам, которые работают в таких компаниях, как Amazon, JP Morgan и программы сертификации Ferrari, для тех, кто хочет вывести свою карьеру на новый уровень. Чтобы продолжать учиться и продвигаться по карьерной лестнице, вам будут полезны следующие финансовые ресурсы:
- Основные концепции статистики в финансах Основные концепции статистики в финансах Твердое понимание статистики имеет решающее значение для того, чтобы помочь нам лучше понять финансы. Более того, концепции статистики могут помочь инвесторам отслеживать
- Субъективная вероятность Субъективная вероятность Субъективная вероятность – это вероятность того, что что-то произойдет, основанная на собственном опыте или личном суждении человека. Субъективный
- Независимые события Независимые события В статистике и теории вероятностей независимые события – это два события, в которых возникновение одного события не влияет на возникновение другого события.
- Количественный анализ Количественный анализ Количественный анализ – это процесс сбора и оценки поддающихся измерению и проверке данных, таких как выручка, доля рынка и заработная плата, чтобы понять поведение и эффективность бизнеса. В эпоху информационных технологий количественный анализ считается предпочтительным подходом к принятию обоснованных решений.
A probability that is unaffected by previous or future events
What is Unconditional Probability?
Unconditional probability, also known as marginal probability, refers to a probability that is unaffected by previous or future events. In other words, unconditional probability is the probability of an event regardless of the preceding or future occurrence of other events. In simplest terms, unconditional probability is simply the probability of an event occurring.
Summary:
- Unconditional probability refers to a probability that is unaffected by previous or future events.
- The unconditional probability of event “A” is denoted as P(A).
- A conditional probability, contrasted to an unconditional probability, is the probability of an event that would be affected by another event.
Formula for Unconditional Probability
Therefore, the unconditional probability of an event happening is simply the probability of the event itself. An unconditional probability does not have a condition.
For example, the probability of rain tomorrow in itself is an unconditional probability.
Further examples of unconditional probabilities:
- What is the probability of a dice rolling a 6?
- What is the probability of landing a head on a coin toss?
- What is the probability of drawing an ace of spades in a deck of cards?
Unconditional Probability vs. Conditional Probability
A conditional probability, contrasted to an unconditional probability, is the probability of an event of which would affect or be affected by another event. In other words, a conditional probability, as the name implies, comes with a condition.
For example, recall the following unconditional probability: “What is the probability of rain tomorrow?” A conditional probability can be phrased as follows: “What is the probability of rain tomorrow, given today is sunny?”
Further examples of conditional probabilities:
- What is the probability of rolling a 6 followed by a 4?
- What is the probability that it is sunny today given that it rains tomorrow?
- What is the probability of the S&P 500 hitting all-time highs and then consolidating at 3,000?
Example of Unconditional Probability
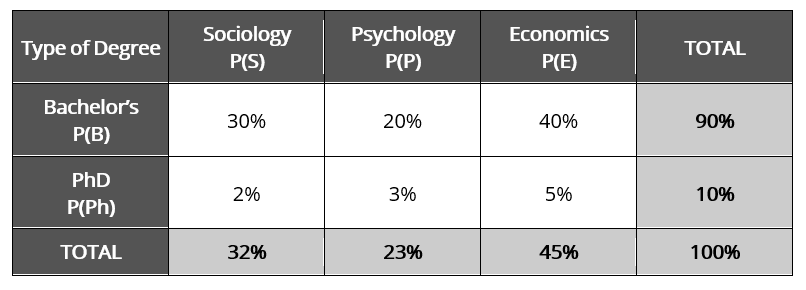
The following joint probability table shows the distribution of Social Science students in a Bachelor’s and Ph.D. programs:
Using your understanding of unconditional probability, determine:
- The unconditional probability of randomly selecting a student who is pursuing a bachelor’s degree;
- The unconditional probability of randomly selecting a student who is studying Sociology;
- The unconditional probability of randomly selecting a student who is pursuing a Ph.D.; and
- The unconditional probability of randomly selecting a student who is studying Economics.
Answers:
- P(B) = 90%
- P(S) = 32%
- P(Ph) = 10%
- P(E) = 45%
Unconditional Probability in the News
Unconditional probability can be commonly found in the news. For example, according to a CNBC article, the CME Group’s FedWatch tool showed traders pricing in a 100% probability of an interest rate cut in July 2019. This, in itself, is an example of an unconditional probability.
Additional Resources
CFI offers the Financial Modeling & Valuation Analyst (FMVA)™ certification program for those looking to take their careers to the next level. To keep learning and advancing your career, the following CFI resources will be helpful:
- Basic Statistics Concepts in Finance
- Subjective Probability
- Independent Events
- Quantitative Analysis
- See all data science resources
Рассмотренная
выше классическая вероятность события
является безусловной вероятностью,
хотя она и рассматривается для некоторого
комплекса условий. Условная же вероятность
кроме известного комплекса условий
определяется дополнительным условием
(или условиями).
Пример 17.
Проводится испытание по бросанию кубика.
Найти вероятность события А2
при условии, что событие В
уже наступило: А2
= {Выпало два очка}, В
= {Выпало четное число очков}.
Решение.
Так как В
произошло, то могли произойти три события
А2 = {Выпало
два очка}, А4 = {Выпало
четыре очка}, А6 = {Выпало
шесть очков}. Если событие В
добавить к комплексу условий, то
получится, что у данного испытания три
элементарных исхода и один благоприятствующий
событию А2
Р(А2
В)
– вероятность события А2
при условии наступления В
равна 1/3.
Определение 25.
Условной вероятностью события А
при условии события В
(Р(В)
0) называют отношение вероятности
произведения этих событий к вероятности
события В:
Р(А
В)
= Р(А
В)
/ Р(В).
Пример 18.
Найти вероятность того, что в группе из
20 человек нет родившихся в один день
при условии события В
= {Все присутствующие родились в один
месяц}.
Решение.
Используем определение условной
вероятности для нахождения Р(А
В),
где А
= {В группе из 20 человек нет родившихся
в один день года}. А
В
= {Все 20 человек родились в разные дни
одного месяца}. Составим список
присутствующих и каждому припишем его
день рождения. Тогда: если в месяце N
дней, то получим для него
списков,
благоприятствующих событию А
В;
общее число элементарных исходов
(списков) равно
,
т.е. могут встретиться люди, родившиеся
в один день любого месяца. Следовательно:
20 человек могли родиться в любой месяц
года, и эти случаи несовместимы, по
аксиоме III
имеем:
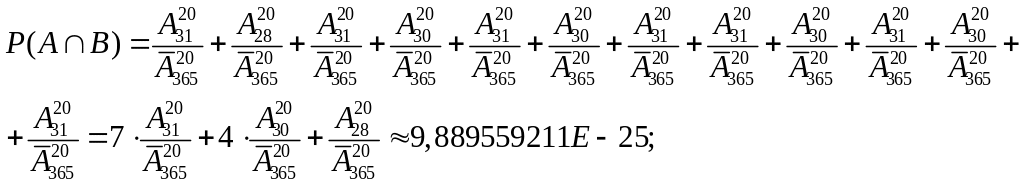
Р(А
В)
= 0,000315951.
Определение 26.
События А
и В
называют независимыми, если условная
вероятность события А
при условии В
совпадает с безусловной вероятностью
события А:
Р(А
В)
= Р(А).
Пример 19.
Определить, являются ли указанные
события независимыми: А
= {Выпало простое число очков}, В
= {Выпало нечетное число очков}.
Решение:
Р(А
В)
=
события
А
и В
не являются независимыми, т.е. они
зависимые события.
Теорема 4.
Если событие
А
не зависит от В,
то и событие В
не зависит от А
[Если Р(А
В)
= Р(А),
то Р(В
А)
= Р(В)].
Теорема 5.
Если событие А
и В
независимы, то независимы будут пары
событий:
2.4. Теоремы сложения и умножения вероятностей
Теорема 6.
Вероятность произведения двух независимых
событий равна произведению вероятностей
этих событий:
Теорема 7.
Вероятность произведения двух зависимых
событий равна произведению вероятности
одного из них на условную вероятность
другого при условии первого события:
Р(А
В)
= Р(А)
Р (В
А).
Теорема 8.
Вероятность суммы двух совместимых
событий А
и В
равна сумме вероятностей этих событий
без вероятности их произведения:
Пример 20.
Два снайпера стреляют одновременно по
цели, которая считается пораженной,
если есть хотя бы одно попадание. Найдите
вероятность поражения цели, если
известно, что вероятность попадания по
цели для первого и второго снайпера
равна соответственно 0,85 и 0,92.
Решение.
Пусть А
= {Попадание 1-го снайпера}и В
= {Попадание 2-го снайпера}. Тогда
Пример
21. Биатлонист
стреляет по мишени. Вероятность выбить
9 очков равна 0,6, и вероятность выбить
10 очков равна 0,25. Найдите вероятность
того, что биатлонист выбьет не менее 9
очков.
Решение.
Пусть А
= {Выбито 9 очков}, В
= {Выбито 10 очков}. Тогда
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое Безусловная вероятность?
Безусловная вероятность — это шанс того, что один результат окажется среди нескольких возможных. Термин относится к вероятности того, что событие произойдет независимо от того, имели ли место какие-либо другие события или присутствовали какие-либо другие условия.
Вероятность выпадения снега в Джексоне, штат Вайоминг, в День сурка, без учета исторических погодных условий и климатических данных для северо-западного штата Вайоминг в начале февраля, является примером безусловной вероятности.
Безусловную вероятность можно противопоставить условной вероятности .
Ключевые моменты
- Безусловная вероятность отражает вероятность того, что какое-то событие произойдет без учета каких-либо других возможных влияний или предшествующих результатов.
- Например, вероятность того, что при честном подбрасывании монеты выпадет орел, имеет безусловную вероятность 50% независимо от того, сколько подбрасываний монеты ему предшествовало, а также от того, произошло ли какое-либо другое событие.
- Безусловная вероятность также известна как предельная вероятность.
Понимание безусловной вероятности
Безусловную вероятность события можно определить, сложив результаты события и разделив их на общее количество возможных исходов.
п(А) знак равно Нумбет ое тямес ‘А» ОссурыТотлНумберуплотнительногофPOSSIблеОутсомеы P (A) = frac { text {Количество раз `} A text {‘Происходит}} { text {Общее количество возможных результатов}}P(А) знак равно Общее количество возможных результатов
Безусловная вероятность также известна как предельная вероятность и измеряет вероятность возникновения события, игнорируя любые знания, полученные из предыдущих или внешних событий. Поскольку эта вероятность игнорирует новую информацию, она остается постоянной.
С другой стороны, условная вероятность — это вероятность наступления события или результата, но основанная на наступлении некоторого другого события или предшествующего результата. Условная вероятность вычисляется путем умножения вероятности предшествующего события на обновленную вероятность успешного или условного события.
Условная вероятность часто изображается как «вероятность того, что A дано B», обозначаемая как P (A | B). Безусловная вероятность также отличается от совместной вероятности , которая вычисляет вероятность того, что два или более исхода происходят одновременно, и изображается как «вероятность A и B», записанная как P (A ∩ B). По сути, он включает безусловные вероятности A и B.
Пример безусловной вероятности
В качестве гипотетического примера из финансов давайте рассмотрим группу акций и их доходность. Акция может быть либо выигрышной, которая приносит положительную доходность, либо проигравшей, которая имеет отрицательную доходность. Предположим, что из пяти акций акции A и B являются выигрышными, а акции C, D и E — проигрышными. Какова же тогда безусловная вероятность выбора выигрышной акции? Поскольку два результата из пяти возможных дадут победителя, безусловная вероятность равна 2 успехам, разделенным на 5 общих результатов (2/5 = 0,4), или 40%.