Решение задач про билеты лотереи
Понравилось? Добавьте в закладки
После разобранных вероятностных задач на выбор шаров из урны и деталей из ящика, перейдем к еще одной популярной задаче на гипергеометрическую вероятность – задаче о покупке лотерейных билетов. Общая постановка задачи следующая:
В лотерее из $N$ билетов $K$ выигрышные и $N-K$ – билеты без выигрыша. Куплено $n$ лотерейных билетов. Найти вероятность того, что из них ровно $k$ выигрышных (соответственно, $n-k$ безвыигрышных) билетов.

Сначала найдем общее число исходов – это число всех различных способов выбрать любые $n$ билетов из общего числа $N$ продающихся билетов (без учета порядка), то есть число сочетаний $C_N^n$ (см. подробнее про сочетания).
Теперь найдем число всех способов выбрать $k$ выигрышных билетов из $K$ возможных – это сочетания $C_K^k$, и одновременно число всех способов выбрать $n-k$ невыигрышных билетов из $N-K$ возможных – $C_{N-K}^{n-k}$. По правилу произведения перемножая эти числа, получим число исходов, благоприятствующих нашему событию – $C_K^k cdot C_{N-K}^{n-k}$.
Применяя классическое определение вероятности, то есть поделив число благоприятствующих событию исходов на общее число исходов испытания (покупки билетов), придем к искомой формуле:
$$
P=frac{C_K^k cdot C_{N-K}^{n-k}}{C_N^n}. qquad (1)
$$
Видеоурок и шаблон Excel
Посмотрите наш ролик о решении задач про лотерейные билеты в схеме гипергеометрической вероятности, узнайте, как использовать Excel для решения типовых задач.
Расчетный файл Эксель из видео можно бесплатно скачать и использовать для решения своих задач.
Примеры решений задач о покупке лотерейных билетов
Пример 1. Среди 100 лотерейных билетов 2 выигрышных. Вы покупаете 3 билета. Какова вероятность, что вы ничего не выиграете?
Начинаем решение задачи с ввода события $A = $ (Из купленных 3 билетов ни один не выиграет) и общей формулы для нахождения вероятности. Так как речь идет о выборе элементов из некоторого множества, используем классическое определение вероятности $P(A)=m/n$, где $n$ – общее число всех равновозможных элементарных исходов, а $m$ – число исходов, благоприятствующих событию $A$.
Сначала найдем общее число исходов – это число способов выбрать любые 3 билета из 100 возможных. Так как порядок выбора несущественнен, используем формулу сочетаний из 100 элементов по 3: $n=C_{100}^3$.
Теперь переходим к числу благоприятствующих нашему событию исходов. Для этого нужно, чтобы из все 3 билета были без выигрыша. Всего таких билетов $100-2=98$, значит способов выбора $m = C_{98}^3$.
Искомая вероятность:
$$
P(A)=frac{m}{n}=frac{C_{98}^3}{C_{100}^3} = frac{152096}{161700} = 0.941.
$$
Вероятность остаться без выигрыша велика – 94,1% (при этом куплен не один, а целых 3 билета). Впрочем, любая лотерея заведома проигрышна для участника, помните об этом. Не стоит искать схемы и правила выигрыша в лотерею. Их не существует.
Пример 2. Среди 8 лотерейных билетов 4 выигрышных. Наудачу взяли 5 билетов. Определить вероятность того что среди них 2 выигрышных.
Подставляем в формулу (1) значения: $K=4$ выигрышных билета, $N-K=8-4=4$ невыигрышных билета, всего $N=8$ билетов. Выбираем $n=5$ билетов, из них должно быть $k=2$ выигрышных и соответственно, $n-k=5-2=3$ без выигрыша. Получаем нужную вероятность:
$$
P=frac{C_{4}^2 cdot C_{4}^{3}}{C_{8}^5} = frac{6 cdot 4}{56} = 0.429.
$$
Пример 3. В лотерее 24 билета, из них 10 выигрышных и 14 пустых. Найти вероятность того, что из трех вынутых билетов, по крайней мере, один окажется выигрышным.
Введем исходное событие:
$A = $ (Среди 3 вынутых билетов, по крайней мере, один окажется выигрышным),
а также противоположное ему событие, которое можно записать как:
$overline{A} = $ (Все три выбранные билеты будут без выигрыша).
Будем искать вероятность события $overline{A}$. Выпишем значения параметров: $K=10$ выигрышных билетов, $N-K=14$ невыигрышных (пустых) билета, всего $N=24$ билета. Выбираем $n=3$ билета, из них должно быть $k=0$ выигрышных и соответственно, $n-k=3$ без выигрыша. Подставляем в формулу (1) и получаем:
$$
P(overline{A})=frac{C_{10}^0 cdot C_{14}^{3}}{C_{24}^3} = frac{1 cdot 364}{2024}= 0.18.
$$
Тогда вероятность искомого события (что будет хотя бы один выигрышных билет), равна:
$$
P(A)= 1 – P(overline{A})= 1- 0.18 = 0.82.
$$
Пример 4. В розыгрыше лотереи участвуют 100 билетов, среди которых 25 выигрышных. Какова вероятность остаться без выигрыша, приобретя 3 билета лотереи?
Подставляем в формулу (1) значения: $K=25$ выигрышных билетов, $N-K=100-25=75$ невыигрышных билета, всего $N=100$ билетов участвует в розыгрыше лотереи. Выбираем $n=3$ билета, из них должно быть $k=0$ выигрышных и соответственно, $n-k=3$ без выигрыша. Приходим к ответу:
$$
P=frac{C_{25}^0 cdot C_{75}^{3}}{C_{100}^3} = frac{1 cdot 67525}{161700} = 0.418.
$$
Спасибо за ваши закладки и рекомендации
Полезные ссылки
- Задачи о лотерейных билетах в схеме Бернулли
- Онлайн учебник по теории вероятностей
- Решенные контрольные по теории вероятностей
- Заказать работу по теории вероятностей
Поищите готовые задачи в решебнике:

Чтобы посчитать точное количество, заменим каждую из трёх последних цифр на дополняющую её до 9. D заменим на K = (9 – D), E на M = (9 – E), F на N = (9 – F). Так как исходно A + B + C = D + E + F, то теперь для числа ABCKMN:
A + B + C + K + M + N
=
A + B + C + 9 – D + 9 –E + 9 – F
=
27
Итак, количество счастливых билетов в точности равно количеству чисел от 000000 до 999999, сумма цифр которых равна 27. Стало немного легче, но предстоит ещё немало работы. Сперва вычислим искомое количество. Для этого нарисуем таблицу, в которой по горизонтали укажем количество используемых цифр, а по вертикали — искомую сумму. Таким образом мы последовательно ответим на все вопросы вида «Сколько существует способов представить число k в виде суммы n цифр». Делать это мы будем рекурсивно, то есть выражать большие значения через меньшие. Поехали!
Очевидно, что в первом столбце у нас будет по одному способу получить числа от 0 до 9 (с помощью одной цифры), а всё, что больше 9, — 0 способов.

Далее, если перейти ко второму столбцу и взять, допустим, число на пересечении второго столбца и шестой строки (k = 5), сколько существует способов представить 5 в виде суммы двух цифр? Логика тут простая. В качестве второй цифры мы можем выбрать любой из вариантов от 0 до 5. Если выбираем 0, то сумма всех цифр, кроме второй, должна быть равна 5 (да-да, понятно, что в данном случае «всех, кроме второй» — это только первая цифра, но давайте сразу составим алгоритм в общем виде). Если выбираем в качестве второй цифры 1, то сумма оставшихся должна быть равна 4 и т. д. Но ведь тогда мы просто должны сложить способы из предыдущего столбца — для всех чисел от 0 до 5! И получить 6 вариантов.
Ещё пример: допустим, я хочу заполнить во втором столбце поле для k = 11. Несложно увидеть, что тогда вторая цифра 0 или 1 не даёт ни одного варианта, так как первая не может быть больше 9. Иначе говоря, мы обращаемся к пустым ячейкам первого столбца, которые соответствуют k = 10 и k = 11. Впрочем, можно считать, что там не пустота, а нули — это не важно. Так или иначе, мы должны сложить все варианты из предыдущего столбца, от k = 2 до k = 11. Это даёт 8. Таким же образом заполняем второй столбец. Последнее число мы впишем при k = 18, так как максимальная сумма двух цифр равна 18.
Переходим к третьему столбцу. Давайте ещё раз посмотрим на примере, как он заполняется. Допустим, k = 15. Тогда, поскольку последняя цифра может быть от 0 до 9, сумма первых двух должна быть равна 6, 7, 8, 9, …, 15. А для всех этих чисел мы уже знаем количество способов представить их в виде суммы двух цифр. Берём эти значения из таблички (это числа 7, 8, 9, 10, 9, 8, 7, 6, 5 и 4), складываем их и получаем результат: 73 способа представить 15 в виде суммы трёх цифр.
Действуя аналогично, продолжаем заполнять табличку. Занятие это весьма муторное, но конечное. Особенно если написать программу. Но можно сделать всё и руками — главное, нигде не обсчитаться. И если довести таблицу до шестого столбца, число, соответствующее k = 27, и будет искомым ответом. Если вы не ошибётесь, то получите ровно 55 252.
Как посчитать вероятность выпадения счастливого билета?
Профи
(646),
закрыт
15 лет назад
Дополнен 15 лет назад
Всем спасибо за хорошие ответы! (особенно a z !). Сейчас вчитываюсь в материал 🙂
Пользователь удален
Мастер
(2215)
15 лет назад
Могу порекомендовать почитать хорошую подборку статей на тему счастливых билетов (разной сложности) здесь: http://www.ega-math.narod.ru/Quant/Tickets.htm (в основном, из журнала Квант) . В частности, там вычислено, что из миллиона билетов с шестизначными номерами (от 000 000 до 999 999) счастливых — 55 252, т. е. приблизительно один из каждых 18 билетов является счастливым (точнее, вероятность выпадения счастливого билета — 5.5252 %).
Помимо этого, рассмотрена более общая задача о n-значных счастливых билетах, для них выписана и явная формула, и асимптотика при больших значениях n. В общем, весьма увлекательное чтиво.
Инна Гребнева (Ситникова)
Гуру
(3258)
15 лет назад
…ты увлекаешься прикладной математикой!… забавный вопросик!… а мне часто выпадают… а можно, кстати, еще загнаться… типо в городе 1 000 000 человек проживает, какова вероятность, что он попадет именно человеку m? Если еще взять в расчет, миграционные факторы)))… в общем, без поллитра не разбершься!
Hell’s Highway Driver
Гуру
(2897)
15 лет назад
надо найти количество таких билетов и поделить на общее количество билетов-все подсказал, считай сам: )
на самом деле задачка не очень интересная- нукдная, делающаяся в лоб и требующая вычислений-я такие ненавижу.
хотя модет она и просто как нибудь и изящно решается…
Dims
Просветленный
(26816)
15 лет назад
Конечно.
Если цифр n. то всего вариантов 10^n. Из них выигрышных 10^(n/2).
Итого вероятность выигрыша равна 10^(n/2)/10^n = 10^(n/2-n) = 1/10^(n/2).
Например, если n=8, то p = 1/10000 = 0,01%
Математические формулы в лотерее являются частью теории вероятностей и комбинаторной математики.
Что же мы подразумеваем под этим интуитивным понятием вероятности? С точки зрения математики возможны две различные интерпретации этого сугубо абстрактного понятия. В первой из них понятие вероятности ассоциируется с частотой появления данного события в серии опытов, в каждом из которых анализируемое событие может появиться или не появиться. Такое событие математики называют случайным.
Как вычислить вероятность?
Существует так называемый закон больших чисел, справедливость которого доказывается в теории вероятностей. Согласно этому закону, в любой серии опытов при увеличении их числа, частота появления случайного события всегда стабильно стремится к одной и той же величине и это предельное значение можно принять за вероятность Р(А) (probability — на английском языке):
![]()
Таким образом, согласно этому утверждению, чтобы найти вероятность события, нужно провести достаточно длинную серию опытов и полученную частоту выразить в процентах.
А нельзя ли определить вероятность выигрыша априори, то есть до начала опытов? Оказывается, что в ряде случаев это возможно. Метод, который используется для априорного определения величин вероятности, основан на втором возможном варианте ее интерпретации и состоит он в следующем:
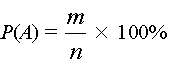
то — есть вероятность появления события А равна отношению числа m — благоприятных событий для А к полному числу n — возможных элементарных событий, выраженному в процентах.
Рассмотрим теперь задачу, более близкую к нашим интересам. А эти интересы в данном случае связаны с подсчетом вероятностей угадывания цифр в розыгрышах Лото 6/49. По правилам этой игры, требуется угадать шесть отобранных (счастливых) номеров из общего количества имеющихся в наличии сорока девяти. Для наглядности заштрихуем «счастливые номера», как это показано на рисунке.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |
Какова вероятность того, что перевернутый номер окажется заштрихованным? Очевидно, она и в этом случае равна отношению числа благоприятных для нас исходов (заштрихованных номеров, а их число равно 6) к полному числу всех возможных исходов (то есть полному числу номеров, число которых 49). Таким образом, вероятность угадать одну из шести отобранных номеров равна 6/49, а вероятность не угадать, соответственно — 43/49.
Если сложить теперь вероятности этих двух возможных исходов, то, как и следовало ожидать, сумма всех вероятностей окажется равной 1. Конечно, хоть что-нибудь, но должно же случиться с достоверностью (то есть с вероятностью 100%). Как говорят, уж если не выиграю, то проиграю.
При второй попытки полное число оставшихся номеров, уже становится равным 48 (один номер уже был разыгран в первом туре). Таким образом, для всех возможных вариантов исхода получаем:
- Если в первом туре был угадан заштрихованный номер:
Вероятность угадать заштрихованный номер становится равно 5/48, а вероятность выпадения незаштрихованного номера составит 43/48. - Если в первом туре был угадан незаштрихованный номер:
Вероятность угадать заштрихованный номер становится равно 6/48, а вероятность выпадения незаштрихованного номера составит 42/48.
Таким образом, при двух подходах жеребьевки возможны четыре варианта результата (первый подход + второй подход):
1) угадал + не угадал: p = 6/49 x 43/48 = 0,1097
2) не угадал + угадал: p = 43/49 x 6/48 = 0,1097
3) угадал + угадал: p = 6/49 x 5/48 = 0,0128
4) не угадал + не угадал: p = 43/49 x 42/48 = 0,7679
Нетрудно убедиться, что и в этом случае сумма вероятностей равна 1.
Как вычислить количество всех возможных результатов?
Легко заметить, что по мере увеличения количества подходов общее количество возможных вариантов результата увеличивается очень быстро, а именно: общее количество возможных вариантов результата для n подходов розыгрышей равно 2n (2 в степени n).
Например, при трех подходах у нас уже будет 23 = 8 возможных вариантов результата:
1) угадал + угадал + угадал: вероятность = 0,0011
2) угадал + угадал + не угадал: вероятность = 0,0117
3) угадал + не угадал + угадал: вероятность = 0,0117
4) не угадал + угадал + угадал: вероятность = 0,0117
5) угадал + не угадал + не угадал: вероятность = 0,0980
6) не угадал + угадал + не угадал: вероятность = 0,0980
7) не угадал + не угадал + угадал: вероятность = 0,0980
8) не угадал + не угадал + не угадал: вероятность = 0,6698
Как вычислить количество комбинаций?
Зная общее количество возможных вариантов, давайте теперь выясним, сколько из этих вариантов содержат угаданные числа. Количество этих вариантов на самом деле является количеством всех возможных комбинаций угаданных заштрихованных чисел.
Предположим, что мы отметили шесть произвольных чисел и хотим узнать, сколько существует вариантов, в которых будет угадано 4 цифры из 6. Число способов, которыми можно угадать 4 из этих 6 номеров, математики называют числом сочетаний и обозначают его ![]() . Эта запись читается так: «число сочетаний из шести по четыре».
. Эта запись читается так: «число сочетаний из шести по четыре».
Предположим, что угаданы числа 12, 14, 30 и 36. Сколько вариантов существует для такого угадывания? Число 12 может быть угадано в любой из 6 попыток, то-есть может быть названо 1-м, 2-м, 3-м, 4-м, 5-м или 6-м. Следовательно, для угадывания числа 12 существует 6 различных вариантов. Второе число 14 может быть угадано в любой из оставшихся пяти попытках, следовательно, для его угадывания имеется 5 различных вариантов. Продолжая эти рассуждения, легко прийти к выводу, что для угадывания числа 30 существует 4 различных варианта, а числа 36 — 3 варианта. Следовательно, для угадывания четверки чисел из шести «счастливых» существуют всего 6х5х4х3 вариантов.
Но не все эти варианты различны. Предположим, что эти числа были угаданы в первых же четырех попытках. Тогда все эти варианты, соответствующие различной последовательности заполнения «счастливых» номеров в тех же самых попытках (всего 24 варианта), фактически представляют 1 вариант (число перестановок 4 элементов равно 4х3х2х1=24).

Окончательно для искомого числа сочетаний мы получили формулу:
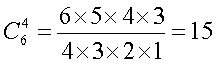
Эта формула для числа сочетаний является справедливой и при любых других количествах отмеченных чисел и количествах «угаданных». В общем случае можно сформулировать следующее правило: для того, чтобы определить количество возможных вариантов с m угаданными числами для отмеченных n чисел, необходимо вычислить число сочетаний:
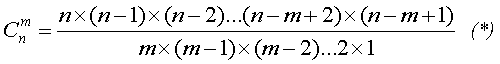
В этой формуле число сомножителей в числителе и знаменателе одинаково и равно m.
Также по этой формуле рассчитывается общее количество возможных комбинаций для игр в лотереи. А для Лото 6 из 49 получаем:
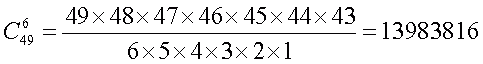
На основе формулы (*) заполняется таблица с количеством выигрышей для каждой категории выигрышей, в зависимости от того, сколько чисел было отмечено и сколько чисел было угадано. См. В качестве примера таблицу для Лото 6/49.
Средний выигрыш одной комбинации
Теперь перейдем к оценке выигрышей, которые рассчитываются на основе среднего выигрыша одного игрового варианта, разыгранного для каждой призовой категории. Средний выигрыш представляет собой вероятность возникновения этого выигрыша, умноженную на общую сумму денег, предложенную для данной призовой категории.
Согласно математическим расчетам, средние значения выигрыша для каждого рубля, потраченного в простой игровой системе и в развернутой игровой системе, одинаковы, независимо от того, сколько чисел было отмечено. Но все же различие между этими двумя игровыми системами существует.
Если мы возьмем статистическую характеристику для большого количества участников игры, то заметим, что при увеличении количества отмеченных чисел в билете в целом, выигрыши становятся крупнее, но вероятность более мелких выигрышей при этом резко уменьшается. Отсюда можно сделать вывод, что если вы стремитесь только к крупному выигрышу, то для вас предпочтительнее будет развернутая система игры, но если не любите сильно рисковать и считаете, что лучше иметь «синицу в руках, чем журавля в небе», то лучше подойдет простая система игры.
Вероятность последовательных неудач
Какова вероятность длинной серии неудач, если ставить в каждом туре на одну и ту же комбинацию? Существует формула, которая называется формулой Бернулли. Она позволяет найти вероятность того, что в результате участия в n турах игры количество туров без единого выигрыша будет равно m:
![]()
где q определяет вероятность «несчастного» случая только для одного тура т.е. не были угаданы 6, 5 и 4 номеров и определяется формулой:
![]()
где ![]() ,
, ![]() и
и ![]() вероятности угадывания 4-х, 5-ти и 6-ти чисел соответственно.
вероятности угадывания 4-х, 5-ти и 6-ти чисел соответственно.
Для примера, на основе формулы Бернулли и некоторых исходных статистических данных были получены следующие результаты вероятностей неудач для 4 розыгрышей:
1) Не было ни одного выигрыша: m = 4, P = 0,02 (2%)
2) Был один выигрыш: m = 3, P = 0,13 (13%)
3) Было два выигрыша: m = 2, P = 0,33 (33%)
4) Было три выигрыша: m = 1, P = 0,37 (37%)
5) Все туры были выигрышными: m = 0, P = 0,15 (15%)
2% + 13% + 33% + 37% + 15% = 100%
Как видим, вероятность последовательных проигрышей с одной и той же комбинацией чисел уменьшается с увеличением количества участий, но появление выигрыша не гарантирует того, что он будет большим.
И все-таки, несмотря на то, что непредсказуемость результатов азартной игры является ее основной чертой, нельзя ли избрать какую-то оптимальную стратегию? Единственный совет, который можно дать в этом случае — это рационально выбрать определенную систему игры и последовательно придерживаться её.
Число «счастливых’’ билетов | Математика, которая мне нравится
Сначала немного истории. Автобусные билеты имели (да и сейчас это, кажется, так же) номера, состоящие из шести цифр. Разумеется, номер билета мог начинаться на . “Счастливыми’’ назывались билеты, у которых сумма первых трех цифр равна сумме последних трех цифр. Была распространена уверенность (во всяком случае, среди детского населения страны), что если тебе достался “счастливый’’ билет, ты можешь загадать желание и съесть билет, тогда твое желание исполнится. Отсюда название. Конечно же, “счастливые’’ билеты доставались ребятишкам не так уж часто. Честно говоря, ни разу не видела, чтобы кто-нибудь такой билет действительно съел, да и сама не ела. Хотя слухи о съевших “счастливый’’ билет и взамен получивших исполнение желания, ходили, и многие были убеждены в том, что они основаны на реальных событиях Соответственно, поскольку билетов таких было не так уж много, возникла и следующая задача о числе “счастливых’’ билетов. Итак,
задача. Каждый из миллиона билетов пронумерован последовательностью из шести цифр (от до ). Сколько существует билетов, у которых сумма первых трех цифр равна сумме последних трех цифр?
В наше время эта задача была достаточно известной. Мне, помнится, она была предложена на уроке алгебры в 9 классе, когда изучали комбинаторику. Кроме того, на тему “счастливых’’ билетов были статьи в журнале “Квант’’ (например, их можно найти здесь). Но удивительно то, что сейчас почему-то пишут о других методах подсчета числа “счастливых’’ билетов, совсем не о комбинаторных, как это было раньше. В основном предлгается программа, написанная на одном или другом языке программирования, которая позволяет решить эту задачу. Забавно, что в написании такой программы ничего сложного нет, это всего лишь цикл, т.е. вещь достаточно стандартная и скучная. А вот попытаться решить задачу с помощью комбинаторики гораздо интереснее и полезнее. Надеюсь, вы это сделаете, прежде чем начать читать дальше .
Решение.
Само решение требует достаточно большого числа вычислений, однако они не очень сложные. Важно понять, как их сократить.
Найдем — число билетов, у которых сумма первых трех цифр равна сумме трех последних цифр и равна . Ясно, что может принимать значения от (три ) до (три “девятки’’).
Сначала докажем, что . В самом деле, каждой последовательности из трех десятичных цифр с суммой цифр от до можно поставить в соответствие последовательность из трех десятичных цифр с суммой цифр следующим образом: каждую цифру в исходной последовательности заменим на цифру . Тем самым, каждой последовательности из трех десятичных цифр с суммой цифр от до будет соответствовать одна и только одна последовательность из трех десятичных цифр с суммой цифр , принимающей значения от до . Значит, таких последовательностей с суммой цифр , где столько же, сколько последовательностей с суммой цифр ().
Далее нам понадобится число способов представления целого неотрицательного числа в виде суммы трех целых неотрицательных слагаемых. Это можно сделать способами. Действительно, число способов равно числу сочетаний с повторениями из по (или иначе, разбиваем единиц на три группы — три слагаемых, в качестве разделителей используем нули, всего элемента, из которых нужно выбрать нуля, см. сочетания с повторениями).
Число способов получить сумму от до можно вычислить по полученной формуле:
: (впрочем, это и так очевидно, , иначе никак),
: ,
: ,
,
: ,
: ,
: ,
: ,
: ,
: .
Теперь перейдем к . Здесь все немного сложнее, потому что цифры не существует, и нам нужно из всех способов разбиения числа не три целых неотрицательных слагаемых вычесть те способы, в которых одно из слагаемых равно . Подсчитать эти способы можно довольно легко. Мы первое слагаемое в разложении числа на сумму трех слагаемых положим равным , а дальше подсчитаем количество способов представить оставшееся число () в виде суммы трех целых неотрицательных слагаемых (этих способов ). Получаем (с учетом того, что слагаемое может стоять на трех разных местах)
: .
Для поступаем точно так же. Сначала находим число способов представить в виде суммы трех целых неотрицательных слагаемых — оно равно , а затем вычитаем те способы, в которых одно из слагаемых больше либо равно десяти — их всего . Итак,
: ,
: ,
: .
Число билетов, у которых сумма первых трех цифр равна сумме последних трех цифр и равна , находится как (независимо от способа выбора первых трех цифр с суммой мы можем выбрать три последние цифры, сумма которых также равна ).
Осталось найти общую сумму:
Итак, всего есть “счастливых’’ билета.
hijos.ru
Математика удачи: Ищем счастливые билеты
Чтобы посчитать точное количество, заменим каждую из трёх последних цифр на дополняющую её до 9. D заменим на K = (9 – D), E на M = (9 – E), F на N = (9 – F). Так как исходно A + B + C = D + E + F, то теперь для числа ABCKMN:
A + B + C + K + M + N
=
A + B + C + 9 – D + 9 –E + 9 – F
=
27
Итак, количество счастливых билетов в точности равно количеству чисел от 000000 до 999999, сумма цифр которых равна 27. Стало немного легче, но предстоит ещё немало работы. Сперва вычислим искомое количество. Для этого нарисуем таблицу, в которой по горизонтали укажем количество используемых цифр, а по вертикали — искомую сумму. Таким образом мы последовательно ответим на все вопросы вида «Сколько существует способов представить число k в виде суммы n цифр». Делать это мы будем рекурсивно, то есть выражать большие значения через меньшие. Поехали!
Очевидно, что в первом столбце у нас будет по одному способу получить числа от 0 до 9 (с помощью одной цифры), а всё, что больше 9, — 0 способов.
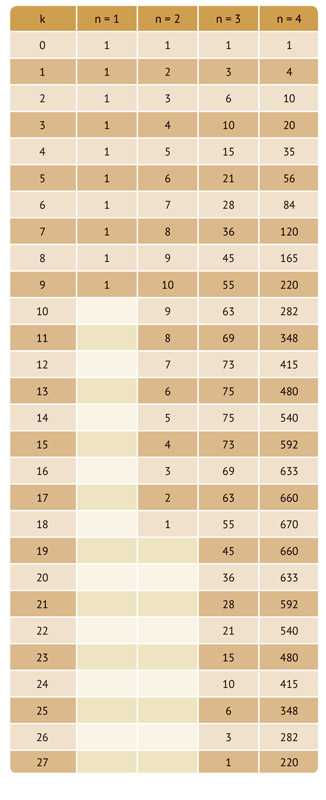
Далее, если перейти ко второму столбцу и взять, допустим, число на пересечении второго столбца и шестой строки (k = 5), сколько существует способов представить 5 в виде суммы двух цифр? Логика тут простая. В качестве второй цифры мы можем выбрать любой из вариантов от 0 до 5. Если выбираем 0, то сумма всех цифр, кроме второй, должна быть равна 5 (да-да, понятно, что в данном случае «всех, кроме второй» — это только первая цифра, но давайте сразу составим алгоритм в общем виде). Если выбираем в качестве второй цифры 1, то сумма оставшихся должна быть равна 4 и т. д. Но ведь тогда мы просто должны сложить способы из предыдущего столбца — для всех чисел от 0 до 5! И получить 6 вариантов.
Ещё пример: допустим, я хочу заполнить во втором столбце поле для k = 11. Несложно увидеть, что тогда вторая цифра 0 или 1 не даёт ни одного варианта, так как первая не может быть больше 9. Иначе говоря, мы обращаемся к пустым ячейкам первого столбца, которые соответствуют k = 10 и k = 11. Впрочем, можно считать, что там не пустота, а нули — это не важно. Так или иначе, мы должны сложить все варианты из предыдущего столбца, от k = 2 до k = 11. Это даёт 8. Таким же образом заполняем второй столбец. Последнее число мы впишем при k = 18, так как максимальная сумма двух цифр равна 18.
Переходим к третьему столбцу. Давайте ещё раз посмотрим на примере, как он заполняется. Допустим, k = 15. Тогда, поскольку последняя цифра может быть от 0 до 9, сумма первых двух должна быть равна 6, 7, 8, 9, …, 15. А для всех этих чисел мы уже знаем количество способов представить их в виде суммы двух цифр. Берём эти значения из таблички (это числа 7, 8, 9, 10, 9, 8, 7, 6, 5 и 4), складываем их и получаем результат: 73 способа представить 15 в виде суммы трёх цифр.
Действуя аналогично, продолжаем заполнять табличку. Занятие это весьма муторное, но конечное. Особенно если написать программу. Но можно сделать всё и руками — главное, нигде не обсчитаться. И если довести таблицу до шестого столбца, число, соответствующее k = 27, и будет искомым ответом. Если вы не ошибётесь, то получите ровно 55 252.
oyla.xyz
Счастливые билетики / Блог им. unC0Rr / OpenLife
Про счастливые билеты написано довольно много: оценка количества таких билетов, общая формула для n-значных билетов в m-ичной системе счисления, московская и ленинградская системы определения «счастливости», график распределения счастливых билетов. Как стартовую точку по этой теме, рекомендую статью на Википедии.
Тем не менее, счастливые билеты хранят в себе некоторые пока неисследованные тайны, о которых я расскажу.
Речь пойдёт о распределении счастливых билетов. Количество шестизначных счастливых билетов равняется 55252, следовательно, вероятность получить такой билет равняется 0,055252. Но какова вероятность получить счастливый билет в случае, когда вы едете не один, и покупаете сразу несколько билетов? Теория вероятностей не помогает ответить на этот вопрос, поскольку речь идёт о нескольких билетах подряд, а не о случайной выборке билетов.
Для исследования вопроса воспользуемся программой на языке Haskell, которая рассчитает интересующие нас данные методом перебора, и рассмотрим случаи московской и ленинградской систем на шестизначных билетиках.
Определим множество всех билетов:
> bilets = [0..999999]и функции определения счастливости по московской и ленинградской системе:
> -- сумма цифр на чётных позициях равна сумме цифр на нечётных
> isLuckyL a =
> ((a `mod` 10) + ((a `div` 100) `mod` 10) + ((a `div` 10000) `mod` 10))
> == (((a `div` 10) `mod` 10) + ((a `div` 1000) `mod` 10) + ((a `div` 100000) `mod` 10))
> -- сумма первых трёх цифр равна сумме последних трёх
> isLuckyM a =
> ((a `mod` 10) + ((a `div` 10) `mod` 10) + ((a `div` 100) `mod` 10))
> == (((a `div` 1000) `mod` 10) + ((a `div` 10000) `mod` 10) + ((a `div` 100000) `mod` 10))
Нам нужно определить для каждой последовательности из нескольких билетов подряд, есть ли в ней хотя бы один счастливый. Для этого определим список distances, который будет хранить в себе расстояние от билетика до следующего счастливого.
> distances = map distance tickets
> where
> distance ticket = if isLuckyL ticket then 0 else 1 + distance (ticket + 1)Теперь легко узнать, сколько существует групп из n последовательных билетов, среди которых есть хотя бы один счастливый, применив фильтрацию по расстоянию.
> counts a = show a ++ ": " ++ show (length $ filter (a > ) distances)
Выведем количество таких последовательностей для всех последовательностей длиной от 1 до 1000.
> main = putStrLn $ unlines $ map counts [1..1000]Применяя в функции distances isLuckyL или isLuckyM, получим данные для ленинградской или московской систем соответственно.
Теперь самое интересное — анализ данных. Построим график зависимости количества счастливых последовательностей билетиков от их длин:
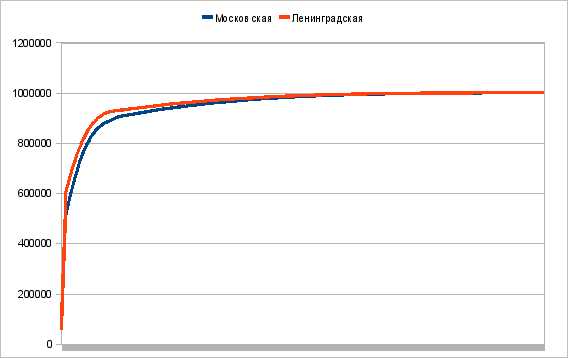
Из графика видно, что ленинградская система на некотором промежутке длин даёт большую вероятность получить счастливый билетик, чем московская. По данным программы, при длинах от 1 до 10 вероятности в обеих системах равны, а при больших длинах ленинградская система выгоднее московской. Так, при 11 билетиках подряд шанс получить счастливый билет по московской системе 506269 из миллиона, по ленинградской — 552511 из миллиона, то есть на 4,6% выше.
Из полученных данных следует, что при езде вдесятером у вас есть неплохие шансы на счастливый билет (49,7%), если конечно, он достанется именно вам. Также, при езде большими группами выгоднее придерживаться ленинградской системы.
P.S. Текст заметки является программой на Literate Haskell.
open-life.org
Счастливый билет — это… Что такое Счастливый билет?
Счастли́вый биле́т — поверье и математическое развлечение, основанное на нумерологической игре с номером проездного билета. Счастливым считается полученный в общественном транспорте билет, в шестизначном номере которого сумма первых трёх цифр совпадает с суммой трёх последних. Общее число шестизначных номеров, порождающих счастливые билеты, равно 55251 (55252, если учитывать билет с номером 000000[1]), то есть в среднем примерно один билет из восемнадцати является счастливым.
Игры с использованием счастливых билетов часто применяются в школе для обучения детей арифметике. Однако со счастливыми билетами связаны и более серьёзные математические задачи, поскольку последовательные номера билетов представляют собой числовую последовательность.
Счастливые билеты бывают объектом коллекционирования, поскольку сохранение билета считается необходимым условием для того, чтобы он выполнил свою функцию — принёс удачу. Другой путь привлечь удачу с помощью такого билета — это его съесть (как съедают, например, пятилепестковый цветок сирени).
-
Счастливый билет номер 268736
-
Счастливые билеты в Новосибирске, Мурманске и Краснодаре
Региональные особенности
«Счастливость» билета можно определить несколькими методами. Наибольшее распространение получили три из них:
- Московский — если на автобусном билете напечатано шестизначное число, и сумма первых трёх цифр равна сумме последних трёх, то этот билет считается счастливым.
- Ленинградский, или Питерский (менее распространённый) — если сумма чётных цифр билета равна сумме нечётных цифр билета, то билет считается счастливым (в статье журнала «Квант» именно этот способ назван «московским»). Другой вариант — суммы каждой пары цифр равны.
- Некоторые люди считают билет счастливым, если сумма его цифр является квадратом. Количество таких билетов с шестизначными номерами равно 99153.
Явные формулы
Точное количество счастливых билетов, определяемых как равенство сумм заданных трёх цифр сумме трёх остальных (Московская и Ленинградская системы) можно посчитать по формуле:[2][3]
которая является частным случаем более общей формулы для нахождения количества 2n-значных счастливых билетов в m-ричной системе счисления (в обычных счастливых билетах используется десятичная система счисления с m=10):
Распределение билетов
В московском и ленинградском методах в среднем один из восемнадцати билетов является счастливым. Однако билеты распределены неравномерно, и вероятность встретить счастливый билет сильно зависит от первых его цифр.
Ниже представлено количество счастливых билетов в каждой тысяче.
Значения цветов
Московский способ
Ленинградский способ
Интересные факты
Примечания
См. также
Ссылки
dic.academic.ru
Счастливый билет — Википедия
Счастли́вый биле́т — поверье и математическое развлечение, основанное на нумерологической игре с номером проездного билета.
Счастливым считается полученный в общественном транспорте билет, в шестизначном номере которого сумма первых трёх цифр совпадает с суммой трёх последних. Общее число шестизначных номеров, порождающих счастливые билеты, равно 55251 (55252, если учитывать билет с номером 000000[1]), то есть в среднем примерно один билет из восемнадцати является счастливым. Также существует определение «счастливости», согласно которому совпадать должны не сами суммы, а их числовые корни (или, эквивалентно, остатки при делении на 9) — в таком случае счастливых билетов больше.
Игры с использованием счастливых билетов часто применяются в школе для обучения детей арифметике. Однако со счастливыми билетами связаны и более серьёзные математические задачи, поскольку последовательные номера билетов представляют собой числовую последовательность.
Счастливые билеты бывают объектом коллекционирования, поскольку сохранение билета считается необходимым условием для того, чтобы он выполнил свою функцию — принёс удачу. Другой путь привлечь удачу с помощью такого билета — это его съесть (как съедают, например, пятилепестковый цветок сирени), или же загадать желание разорвать билет по горизонтали и выпустить его через левое плечо
Региональные особенности[править]
«Счастливость» билета можно определить несколькими методами. Наибольшее распространение получили три из них:
- Московский — если на автобусном билете напечатано шестизначное число, и сумма первых трёх цифр равна сумме последних трёх, то этот билет считается счастливым.
- Ленинградский, или Питерский (менее распространённый) — если сумма цифр, стоящих на чётных местах билета, равна сумме цифр, стоящих на нечётных местах билета, то билет считается счастливым (в Санкт-Петербурге, напротив, именно этот способ называют «московским»). Другой вариант — суммы каждой пары цифр равны.
- В журнале «Квант» от июля 1975 [2] года указано, что метод подсчета суммы первых и вторых троек чисел москвичи называют московскими, а ленинградцы — ленинградским, соответственно метод подсчета сумм четных и нечетных позиций приписывают другому городу.
- Некоторые люди считают билет счастливым, если сумма его цифр является квадратом. Количество таких билетов с шестизначными номерами равно 99153.
Точное количество счастливых билетов, определяемых как равенство сумм заданных трёх цифр сумме трёх остальных (Московская и Ленинградская системы) можно посчитать по формуле:[3][4]
которая является частным случаем более общей формулы для нахождения количества 2n-значных счастливых билетов в m-ричной системе счисления (в обычных счастливых билетах используется десятичная система счисления с m=10):
Распределение билетов[править]
В московском и ленинградском методах в среднем один из восемнадцати билетов является счастливым. Однако билеты распределены неравномерно, и вероятность встретить счастливый билет сильно зависит от первых его цифр.
Ниже представлено количество счастливых билетов в каждой тысяче.
Значения цветов
Московский способ
Ленинградский способ
С.К.Ландо Счастливые билеты // Математическое просвещение. — МЦНМО, 1998. —. —.
www.wikiznanie.ru
