Биссектриса параллелограмма делит один из углов при параллельных прямых и секущей (которые задействованы в строении параллелограмма), а так как эти углы в сумме дают 180°, то в пересечении с биссектрисой смежного угла получается перпендикуляр (90°). Это является основным свойством биссектрис параллелограммов и других фигур, имеющих в составе две параллельные стороны, например трапеции.
Найти биссектрису в параллелограмме через сторону и угол можно из полученного при ее построении треугольника. Для этого необходимо провести вторую биссектрису, которая по совместительству будет высотой в этом треугольнике. Учитывая, что треугольник равнобедренный, исходя из равенства углов при основании, его основание-биссектриса будет удвоенным катетом получившегося прямоугольного треугольника, в котором гипотенуза – это сторона параллелограмма, а угол – половина угла параллелограмма.
Выпускники, которые рассчитывают успешно сдать ЕГЭ, в обязательном порядке должны повторить тему «Свойства биссектрисы параллелограмма». Как показывает статистика, при прохождении аттестационного испытания задачи по данному разделу планиметрии вызывают сложности у большого количества учащихся. При этом задания, в которых необходимо применить свойства биссектрисы угла параллелограмма, встречаются в ЕГЭ ежегодно. Таким образом, справляться с ними должны все учащиеся.
Образовательный портал «Школково» предлагает выстроить процесс подготовки к прохождению аттестационного испытания по-новому. Занимаясь вместе с нашим ресурсом, выпускники смогут определить наиболее сложные для себя темы и ликвидировать пробелы в знаниях.
Чтобы задания ЕГЭ не вызывали трудностей, рекомендуем вначале повторить основные понятия и свойства биссектрисы параллелограмма. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».
Для того чтобы окончательно понять принцип решения задач по данному разделу планиметрии, мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий различного уровня сложности представлена в разделе «Каталог». Для каждого упражнения на сайте приведен алгоритм решения и дан правильный ответ. Последовательно выполняя их, учащиеся смогут понять, как правильно применять свойства биссектрисы внутреннего угла параллелограмма.
Получать новые знания и оттачивать собственные навыки по данной теме или, например, в решении задач на тему «Прямоугольник» в ЕГЭ учащиеся могут в онлайн-режиме, находясь в Москве или любом другом российском городе. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
Равнобедренный треугольник в параллелограмме
Биссектриса параллелограмма может быть проведена из вершины острого или тупого угла фигуры. Доказательство теоремы о равнобедренности образуемых прямой треугольников в этих случаях имеет аналогичный порядок. Чтобы доказать утверждение, нужно знать признак равнобедренности треугольника:
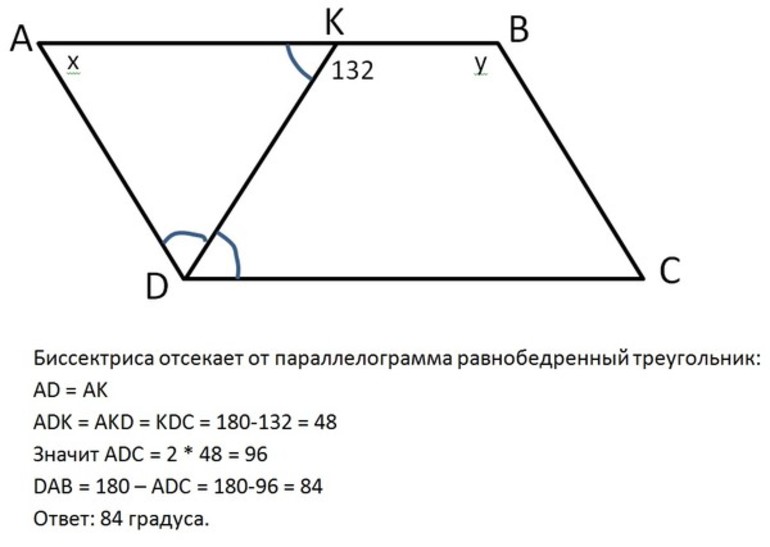
- Согласно условию, проведенная из острого угла А биссектриса AF делит одну из сторон ABCD на 2 отрезка.
- Свойство биссектрисы позволяет утверждать, что углы FAD и BAF равны между собой.
- Определение внутренних накрест лежащих углов, которые образует секущая AF с прямыми ВС и AD, приводит к выводу о равенстве FAD и BFA.
- Поскольку углы BFA и BAF равны, этот признак свидетельствует о равнобедренности треугольника ABF.
- Стороны АВ и BF являются равными и соответствуют отрезку m, который образован при делении ВС биссектрисой.
С помощью аналогичных рассуждений можно доказать, что биссектриса тупого угла параллелограмма делит противоположную сторону на отрезки и отсекает от него равнобедренный треугольник.
Точка пересечения прямых
Согласно свойству, проведенные из смежных углов параллелограмма биссектрисы пересекаются в точке на противоположной стороне, если она в 2 раза больше меньшей. Доказать это утверждение можно следующим способом:
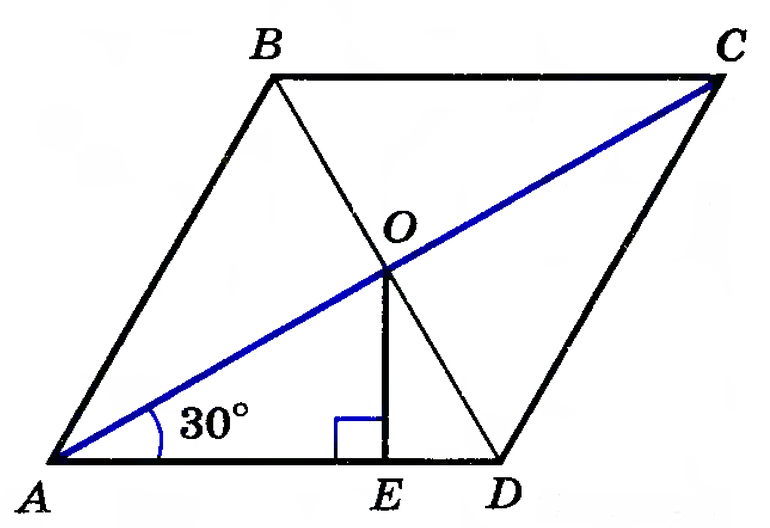
- В равнобедренном треугольнике АВО сторона АО является биссектрисой четырехугольника АВСD.
- Признак равнобедренности предполагает равенство АВ и ВО.
- Согласно свойству, равенство СО и СD свидетельствует о равнобедренности треугольника СDО.
- Стороны АВ и СD равны как противолежащие, из чего следует равенство ВО и СО.
- Поскольку АВ и ВО равны, то ВО = СО, поэтому АВ равна половине ВС, значит большая сторона фигуры в 2 раза превышает величину меньшей.
Доказательство свойства позволяет предположить, что биссектрисы смежных углов пересекаются внутри либо вне параллелограмма. При этом одна сторона больше или меньше половины другой. Если ее величина больше половины соседней, значит прямые пересекутся внутри фигуры.
Биссектрисы, проведенные через смежные углы, пересекаются с продолжением противоположных сторон параллелограмма в вершинах ромба. В зависимости от величины другой стороны, ромб совпадает с ним либо обладает большим или меньшим периметром. Если частить с построением этой фигуры, то длины сторон параллелограмма будут бесконечными.
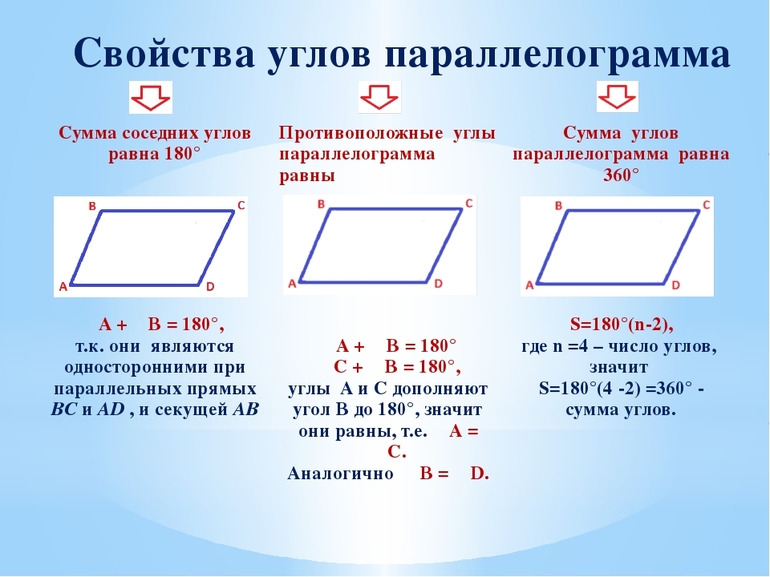
Свойства односторонних углов
Параллелограмм АВСД имеет смежные углы при параллельных прямых АВ и СД, обозначенные а1 и а2. Для доказательства теоремы о перпендикулярности биссектрис нужно знать свойства смежных углов, сумма которых равна 180 градусам.
Поскольку биссектрисы можно провести внутри острого или тупого угла параллелограмма, то величину смежного с ним внешнего угла можно сложить, получив 180 градусов. Если обозначить их через АО и ДЕ, то углы ОАВ и ЕДС будут равны половинам а1 и а2 соответственно. Так как а1 + а2 = 180, то (а1 + а2) / 2 = 90, значит АО и ДЕ образуют прямой угол АКД.
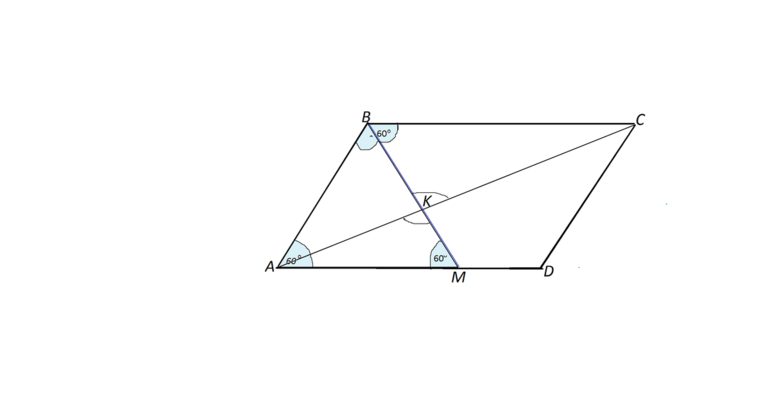
Применять свойство биссектрис можно при нахождении периметра фигуры. Должны быть известны данные о соотношениях или длинах отрезков, образованных при пересечении противолежащей стороны биссектрисой. Например, она делит на отрезки ВК и КС сторону параллелограмма ABCD, величины которых известны.
Формула определения периметра будет иметь вид: P=2 (n+n+m). Где ВС=BК+КC=n+m, а АВ=ВК=n по свойству биссектрисы. С учетом признака равнобедренности треугольника можно построить эту прямую, дополнив рисунок фигуры без транспортира с помощью циркуля.
Противолежащие углы и биссектрисы
Согласно свойству параллельных прямых, биссектрисы a и b проходят параллельно друг другу. Они образуют внутри фигуры со сторонами mnkp другой параллелограмм, следовательно, он обладает параллельными противоположными сторонами. Прямые, на которых они лежат, соответствуют сторонам исходной фигуры, поэтому ее биссектрисы a и b являются равными.
Углы, которые образованы отрезками a и m, а также b и k, согласно свойствам биссектрис и параллелограммов, равны. Противолежащие равные по величине углы, образованные отрезками mp и nk, можно разделить пополам. Прямая b, пересекающая отрезки n и p, образует с ними накрест лежащие углы, признак которых состоит в их равенстве. Они равны разделенным пополам противоположным и являются соответственными при параллельных прямых n и p.
Вершины образуемого прямоугольника
Биссектрисы параллелограмма пересекаются в точках, представляющих собой вершины прямоугольника, что можно доказать следующим образом:
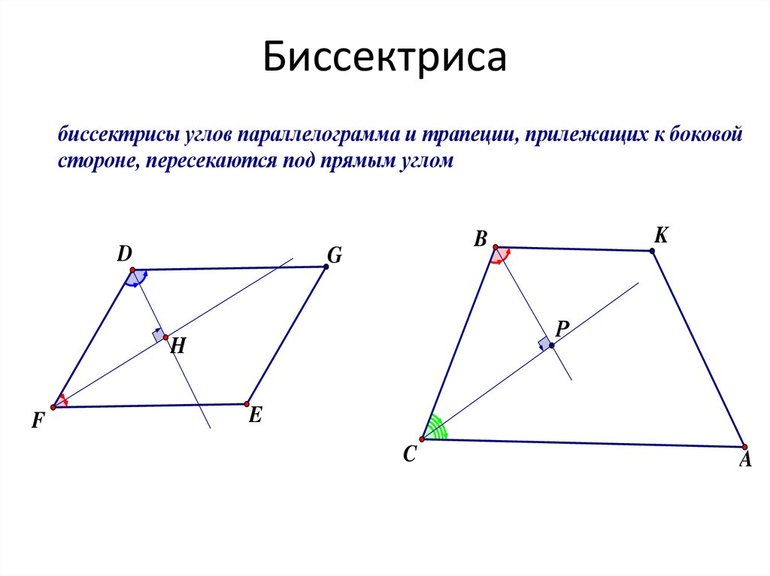
- Согласно исходным данным, параллелограмм ABCД имеет внешние углы, через вершины которых В и С проведены прямые, разделяющие их пополам.
- Если К, М, Р и О представляют собой точки пересечения биссектрис, исходящей из вершин фигуры, то они образуют четырехугольник.
- По свойству смежных внутренних углов, образуемых параллельными прямыми и секущей, все стороны четырехугольника КМРО перпендикулярны между собой.
- Если через середину ВС фигуры провести медиану треугольника ВКС в параллелограмме, то эта точка Х разделит ВС на равные отрезки ВХ и СХ.
- Отсюда следует равенство углов ХКС, КСХ и КСТ, где Т — это точка, принадлежащая прямой СД.
- Вывод из доказательства: прямые СД и КХ параллельны.
Аналогичным способом можно доказать параллельность других сторон прямой СД. Следовательно, диагональ КР образованного биссектрисами параллелограмма прямоугольника КМРО содержит точки Х и Т. Доказательство предполагает следующее равенство: КР = КХ + ХТ + ТР = ХС + СД + ТД = ВС + СД, поэтому величина диагонали равна сумме двух смежных сторон параллелограмма.
Ромб и его диагонали
Параллелограмм, имеющий биссектрису, которая совпадает с его диагональю, представляет собой ромб. Чтобы доказать это, нужно провести диагональ AC, соединяющую противоположные вершины ABCD. Способ доказательства теоремы основан на равенстве противолежащих углов параллелограмма.
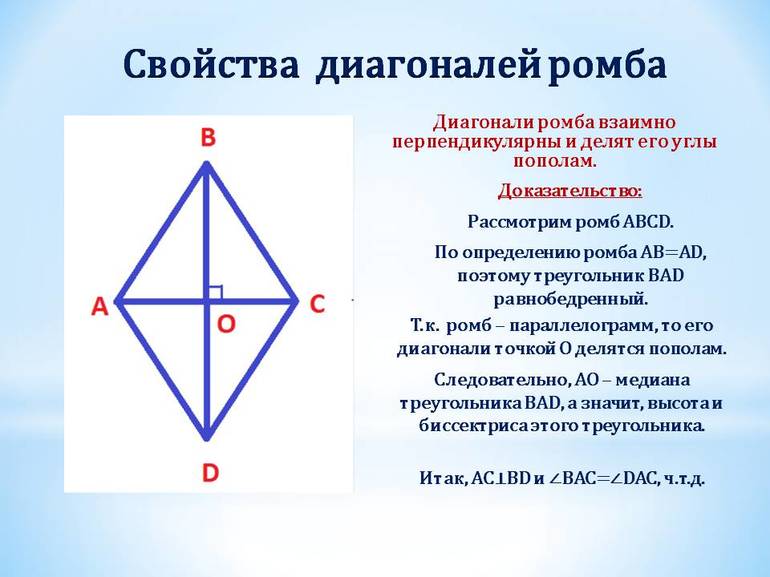
Согласно свойству биссектрисы, отрезок АС делит пополам углы BCD и BAD. Они имеют одинаковую величину, поскольку противоположные углы равны. Диагональ АС — основание треугольников ACB и ACD. Согласно признаку равнобедренности АВ и АС, а также AD и CD, равны между собой. По свойству равенства противоположных сторон параллелограмма AB = CD и AD = BC.
Фигура ABCD, представляющая собой по условию параллелограмм, имеет равные по величине AB, AD, BC и CD в соответствии с доказательством. Отсюда следует, что параллелограмм ABCD по определению ромб. В нем биссектриса АС — это его диагональ.
Примеры решения задач
Биссектрисы смежных углов параллелограмма пересеклись в точке на его противолежащей стороне. Зная его меньшую сторону, можно найти большую, а также наоборот. Допустим, что длина меньшей стороны фигуры составляет 5 сантиметров.
Обозначив вершины фигуры A, B, C, D, а точку на AD буквой Р, достаточно иметь в виду, что AD=AР+РD=AB+CD. Это доказывает признак равенства накрест лежащих углов СВР и АРВ, а также ВСР и СРD при параллельных прямых. Формула для нахождения большей стороны будет иметь вид: AD=2AB=10, поскольку AB = CD. При необходимости найти меньшую можно по формуле: AD=AB/2.
По условию задачи биссектриса, исходящая из острого угла параллелограмма, разделяет его противоположную сторону на отрезки 73 мм и 54 мм, если считать от вершины тупого угла. Требуется вычислить периметр параллелограмма ABCD. Точка Е делит сторону ВС на отрезки заданной длины, поскольку АЕ — биссектриса угла ВАD. Эта прямая представляет собой секущую для параллельных AD и BC.
Отсекая равнобедренный треугольник АВЕ, биссектриса ВЕ является его основанием, поэтому сторона параллелограмма АВ равна отрезку ВЕ, длина которого по условию 73 мм. В сумме ВЕ и ЕС равны ВС, что составляет 127 мм. Отсюда периметр ABCD соответствует удвоенной сумме его сторон: Р = 2 (73+127) = 400 мм. Чтобы найти большую сторону параллелограмма ABCD при известном периметре 128 мм, можно использовать аналогичное доказательство равнобедренности треугольника.
По условию соотношение отрезков, образуемых точкой пересечения биссектрисы DЕ с противоположной стороной ВС, равно 4:3, если считать от острого угла при вершине А. Из равенства противоположных сторон ABCD и признака равнобедренного треугольника следует AD=BC=АЕ=4х, а ЕВ=3х, поэтому CD=АЕ+ЕВ=4х+3х=7х. Зная периметр ABCD, можно составить уравнение Р=2 (7х+4х)=128. Отсюда 22х=128, а х=32, поэтому большая сторона параллелограмма CD=32*7=224 мм.
Свойства биссектрисы параллелограмма
– Биссектриса по определению делит угол пополам
– Биссектриса отсекает равнобедренный треугольник (в данном случае треугольники ABF и DKC)
– Биссектрисы смежных углов, пересекаются под прямым углом (90°)
– Биссектрисы противоположных углов, равны и параллельны
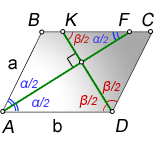AF – биссектриса из острого угла
DK – биссектриса из тупого угла
α – острый угол
β – тупой угол
a – меньшая сторона
b – большая сторона
Так как треугольники ABF и DKC, равнобедренные, следовательно справедливы тождества:
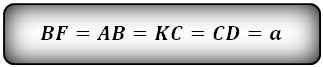
Длина биссектрисы параллелограмма
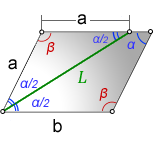
L – биссектриса параллелограмма
a, b – стороны
α, β – углы
Формулы длины биссектрисы через сторону и углы, (L):
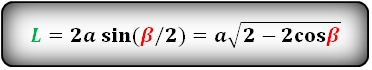
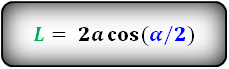
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 07 ноября 2011
-
Обновлено: 13 августа 2021
IV Научно-практическая
конференция городского научного общества учащихся
Биссектриса
параллелограмма
Секция: математика
Авторы:
Тимшин
Владислав Владиславович
МОУ
СОШ № 35,8 Б класс
Домашний
адрес:
Стасова
д.8, кв. 18
Телефон:
63-10-03;
Инейкин
Александр Сергеевич
МОУ
СОШ № 35,8 Б класс
Домашний
адрес:
Станкостроителей
д.8, кв. 83
Телефон:
68-63-91
Научный
руководитель:
Криушина
Галина Михайловна,
МОУ
СОШ № 35,
Учитель
математики высшей квалификационной категории.
г.Ульяновск
2011год.
1.Мотивация.
В 8 классе мы начали изучать параллелограмм. Наиболее интересным в данной теме
для меня показался не сам параллелограмм, а его свойства. На одном уроке у нас
была тема «Применение свойств параллелограмма». Оказалось, что задачу на
применение этих свойств можно решить двумя или трёмя способами.
И
тут нам захотелось расширить свой кругозор по данной теме: какие ещё задачи
можно решить с помощью биссектрисы параллелограмма и как?
Начали
мы исследование с истории возникновения параллелограмма. Термин
“ПАРАЛЛЕЛОГРАММ” греческого происхождения и был введен Евклидом.
Понятие параллелограмма и некоторые его свойства были известны ещё
пифагорейцам.
В
“Началах” Евклида доказывается теорема о том, что в параллелограмме
противоположные стороны равны и противоположные углы равны, а диагональ
разделяет его пополам. Евклид не упоминает о том, что точка пересечения
диагоналей делит их пополам. Он не рассматривает ни прямоугольника, ни ромба.
Полная теория параллелограммов была разработана к концу средних веков и
появилась в учебниках лишь в XVII веке. Все теоремы о параллелограммах
основываются непосредственно или косвенно на аксиоме параллельности Евклида.
В
свою научную работу мы включили:
1).
Проблему расположения биссектрисы относительно сторон параллелограмма
2).
Свойства биссектрис параллелограмма
3).
Доказательство свойств параллелограмма
4).
Мини-доклад про Софью Ковалевскую
Актуальность
выбранной темы заключается в том, что биссектриса параллелограмма имеет широкое
применение в теории, что и является прикладной значимостью. Исследовательский
характер работы состоит в решении задач с применением свойств биссектрисы
параллелограмма, выходящих за рамки школьной программы.
Исследовательский проект
«Биссектриса
параллелограмма».
Мотивация.
При решении задачи №425 (“Геометрия 7-9” Л.С.Атанасян) появились разногласия
по построению рисунка к задаче. Возникла проблема: какую сторону пересечет
биссектриса соседнюю или противоположную? В теоретических знаниях, полученных нами
на уроках геометрии, нигде не встретились свойства биссектрисы параллелограмма.
И тогда мы решили исследовать эту проблему, а наряду с этим попытаться отыскать
ещё какие-нибудь свойства биссектрисы параллелограмма.
Актуальность. При
более подробном знакомстве с данной темой, появляется возможность расширить
полученные в школе знания о параллелограмме и его биссектрисах, и надеемся, в
дальнейшем сможем применять эти знания при решении геометрических задач.
Цель: изучить
свойства биссектрисы параллелограмма.
Задачи
1.Изучить
литературу по выбранной проблеме;
2.Научиться
применять полученные знания при решении геометрических задач;
3.Подобрать различные задачи, связанные с использованием
свойств биссектрисы параллелограмма;
Объект
исследования: биссектриса параллелограмма.
Мы попытались подойти к этому
вопросу практически. Изображая различные параллелограммы, при помощи
транспортира проводили в них биссектрисы, анализировали рисунки и пытались
сделать выводы. Так же использовали бумажные модели параллелограммов.
Проведенная работа позволила нам сформулировать и свойства биссектрис
параллелограмма, а затем и доказать их.
Свойства
биссектрис параллелограмма.
1.Биссектриса угла
параллелограмма отсекает от него равнобедренный треугольник.
2.Биссектрисы
смежных углов параллелограмма пересекаются под прямым углом.
3.Биссектрисы
соседних углов параллелограмма пересекаются на большей стороне параллелограмма,
если она в два раза больше меньшей стороны.
4.Биссектрисы
соседних углов параллелограмма пересекаются внутри параллелограмма, если
меньшая сторона больше половины большей стороны.
5.Биссектрисы соседних
углов параллелограмма пересекаются вне параллелограмма, если меньшая сторона
меньше половины большей стороны.
6.Биссектрисы
соседних углов параллелограмма могут пересекать противоположную сторону или ее
продолжение.
7.Биссектрисы
соседних углов параллелограмма равны и параллельны.
8.Биссектрисы
параллелограмма, пересекаясь, образуют прямоугольник.
Доказательства
этих свойств мы оформили в виде презентации, чтобы затем познакомить с ними
других учащихся.
Заключение:
В процессе
выполнения работы были:
1.Сформулированы
и доказаны свойства биссектрисы параллелограмма.
2. Составлен ряд
несложных заданий для устного решения, которые предложили своим одноклассникам.
3.Составлена тестовая
работа по теме “Биссектрисы параллелограмма”;
4.Сделана подборка
задач по данной теме из различных сборников для подготовки к экзаменам и
сборников олимпиадных заданий.
Мы увидели необходимость
применения этих свойств для решения большого количества задач. В своей работе
мы не только сами сформулировали, доказали свойства, но и попыталась применить
их к решению задач. Я думаю, что на следующий год этот материал будет необходим
нам при подготовке к экзамену по геометрии. Будем рады, если другие ребята
воспользуются им.
