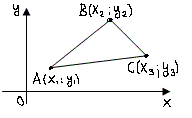Как найти биссектрису первого координатного угла

Помогите понять смысл задания

Alex

Ученик

(203),
закрыт

13 лет назад

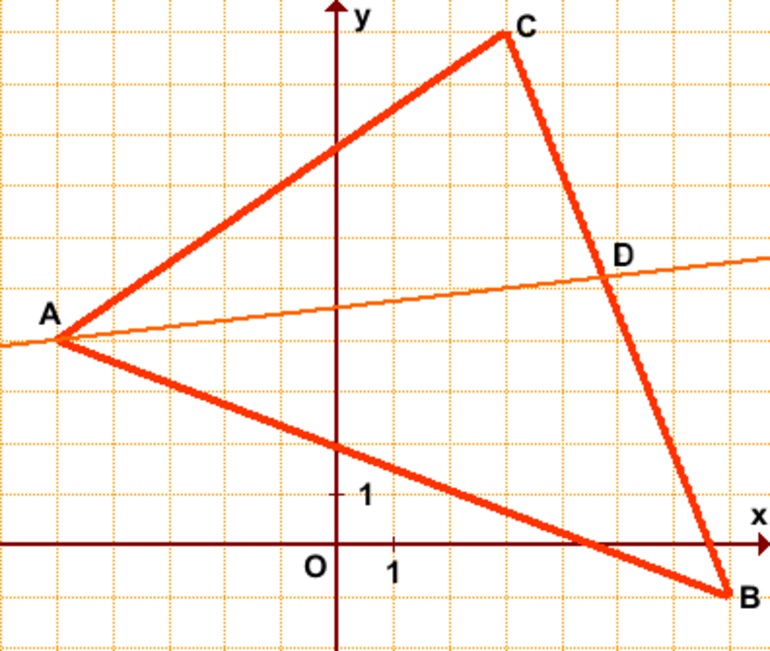
В какой точку параболы y=X^2 -2X + 5 нужно провести касательную чтоб она была перпендикулярна бисиктрисе первого координатного угла?

Прямая на плоскости

Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:

1. На плоскости, где достаточно двух координат для описания любых геометрических объектов.
2. В трехмерном пространстве, где любая точка имеет три координаты.

Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:

1. Общий. Он также называется универсальным. Прямая представляет собой следующую математическую запись: A*x + B*y + C = 0. Здесь A, B, C — числовые коэффициенты, x и y — переменные, являющиеся координатами. Сразу нужно отметить, что эта форма представления прямой используется для составления уравнения биссектрисы угла. Для удобства геометрического изображения общую форму записи часто представляют в виде y = f (x). Нужно понимать, что указанной форме в пространстве соответствует не прямая, а плоскость.
2. Канонический или уравнение в отрезках. Имеет оно такой вид: y/p + x/q = 1. Здесь p, q — это координаты, в которых прямая пересекает оси y и x, соответственно, поэтому удобно ее изображать в координатной системе.
3. Векторный. Это один из важных типов представления прямой как на плоскости, так и в пространстве. По сути, он является исходным представлением, из которого можно получить все остальные. Математически он записывается так: (x, y) = (x0, y0) + α*(v1, v2). Где (x0, y0) — координаты произвольной точки, которая лежит на прямой, (v1, v2) — направляющий вектор, он параллелен заданной прямой, α — произвольное число, параметр.
4. Параметрический. Этот тип представляет собой систему уравнений, которую удобно использовать во время преобразования одного вида прямой в другой. Представляет он собой следующую математическую запись: x = x0 + α*v1; y = y0 + α*v2. Несложно понять, что, выражая параметр α, можно получить уравнения общего вида и в отрезках. Объединяя же систему уравнений в одно выражение, получается векторная форма записи прямой.

Делящая пополам угол линия

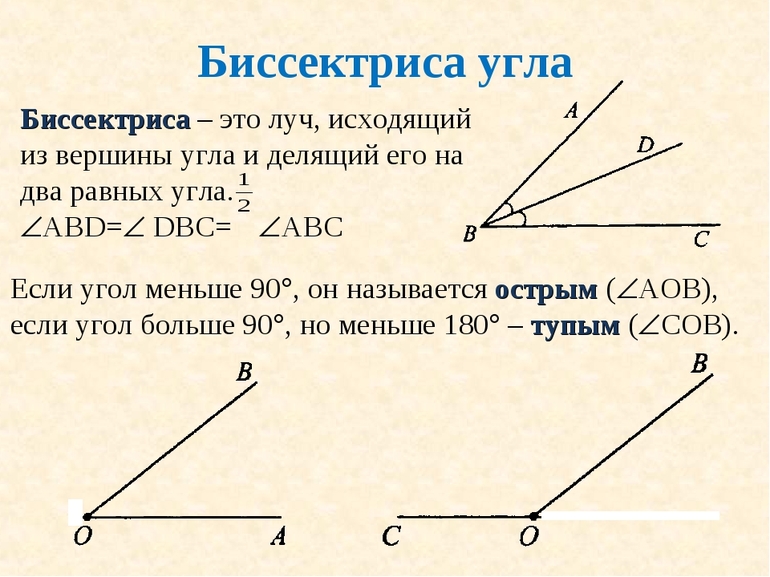
Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.

Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.

Способы построения

В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:

1. С помощью транспортира. Для этого следует измерить заданный угол в градусах, разделить его пополам. Полученное значение отметить в виде точки. Затем соединить вершину угла и поставленную точку внутри него. Получится искомый элемент.
2. С использованием циркуля и линейки. Эти инструменты еще проще применять для построения биссектрисы, чем транспортир. Сначала необходимо установить в вершину угла ножку циркуля и отметить дугами пересечение окружности со сторонами. Затем, в точки пересечения поставить ножку циркуля и провести две окружности. Соединив две точки их пересечения одной прямой, можно получить биссектрису.

Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.

В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.

Основные свойства

Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.

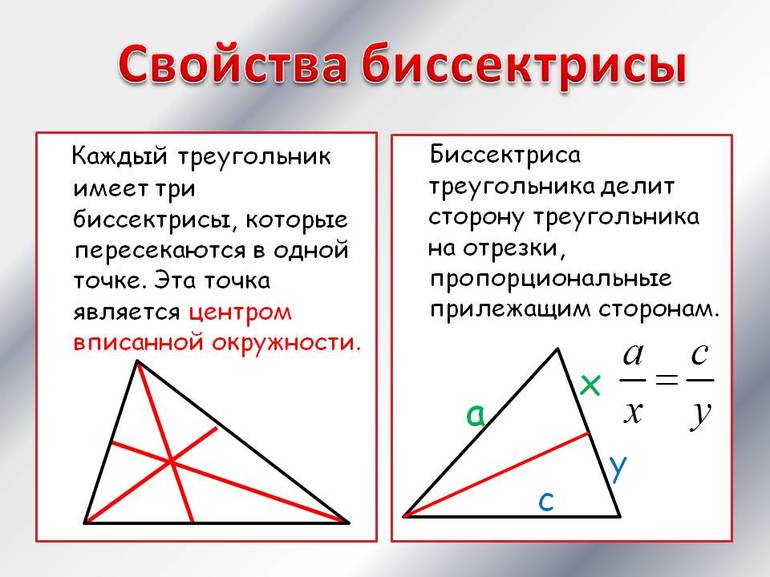
Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.

Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.

В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:

DB/DC = AB/AC.

Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.

Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:

L (A) = 2/(b+c)*(b*c*p*(p-a))^0,5.

Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.

Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.

Уравнение биссектрисы треугольника

Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.

В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):

1. Сначала требуется определить уравнения двух сторон угла по их координатам. Это легко сделать в векторной форме, а затем, преобразовать ее в выражение общего типа.
2. Далее, необходимо найти уравнение биссектрис первого координатного угла, прировняв расстояния от ее точек до соответствующей стороны. Рабочая формула имеет вид: |A1*x + B1*y + C|/(A1 ² + B1 ² )^0,5 = |A2*x + B2*y + C|/(A2 ² + B2 ² )^0,5. Следует обратить внимание на наличие двух различных решений этого равенства, поскольку в числителе стоит модульное выражение. Два полученных уравнения говорят о наличии взаимно перпендикулярных биссектрис для углов треугольника внутреннего и внешнего.
3. Для внутреннего угла искомое уравнение можно найти, если определить точку пересечения соответствующей прямой с противоположной исходному углу стороной треугольника. Та точка, сумма расстояний от которой до концов отрезка будет равна длине стороны, принадлежит искомой биссектрисе.

Пример решения задачи

Пусть, треугольник задан координатами A (1, -1), B (0, -2), C (3,0). Следует уравнение биссектрисы найти для угла B и ее длину вычислить.

Сначала нужно написать уравнения прямых для сторон AB и CB, получается:

• AB: (x, y) = (1, -1) + α*(-1, -1) ==> y — x + 2 = 0;
• CB: (x, y) = (3, 0) + α*(-3, -2) ==> 3*y — 2*x + 6 = 0.

Составить уравнения биссектрис можно так:

| y — x + 2 |/(2)^0,5 = | 3*y — 2*x + 6 |/(13)^0,5.

Решение этого уравнения приводит к следующим двум выражениям для взаимно перпендикулярных биссектрис:

• y*(6−3*3 ^0,5) + x*(3*3 ^0,5 −4)+12−6*3 ^0,5 = 0;
• y*(3*3 ^0,5+6) -x*(4+3*3^0,5)+12+6*3 ^0,5 = 0.

Чтобы определить, какая из двух прямых является искомой для треугольника заданного, следует точку пересечения каждой из них со стороной AC найти. Уравнение для AC имеет вид:

x = 2*y + 3.

Подставляя его в каждое из выражений для биссектрис, можно получить две точки пересечения:

• D1 = (-0,2515;-1,6258);
• D2 = (1,556;-0,722).

При этом длина основания AC составляет 2,236 единицы через единичный вектор. Расстояние от точек D1 и D2 до A, C равно:

• D1A = 1,4; D1C = 3,635;
• D2A = 0,621; D2C = 1,614.

Видно, что точка пересечения второй прямой D2 лежит между A и C, поэтому соответствующее ей уравнение биссектрисы является ответом на задачу. Ее длину можно вычислить по формуле для модуля вектора BD2:

BD2 = 2,014 единицы.

Таким образом, для определения в треугольнике биссектрисы уравнения по координатам следует уметь находить векторную форму выражений для прямой по координатам двух точек. Также нужно знать свойства делящей пополам угол линии.

Простейшие задачи аналитической геометрии на плоскости

1. Расстояние между двумя точками.

Теорема
1.
Для любых двух точек
иплоскости расстояниемежду ними выражается формулой:

.
(1.1)

Например,
если
даны точки
и,
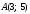
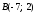
то расстояние между ними:

.

2. Площадь треугольника.

Теорема
2.
Для любых точек

,
не лежащих на одной прямой, площадь
треугольника
выражается формулой:

.
(1.2)

Например,
найдем площадь треугольника, образованного
точками
,и.

.

Замечание.
Если площадь треугольника равна нулю,
это означает, что точки лежат на одной
прямой.

3. Деление отрезка в заданном отношении.

Пусть
на плоскости дан произвольный отрезок

и
пусть

–любая
точка этого отрезка, отличная от точек
концов. Число
,
определенное равенством,
называетсяотношением,
в
котором точка
делит отрезок.

Задача
о делении отрезка в данном отношении
состоит в том, чтобы по данному отношению
и данным координатам точек

и
найти координаты точки.

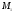
Теорема
3.
Если
точка
делит отрезок
в
отношении

,
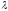
то
координаты этой точки определяются
формулами:
(1.3), где– координаты точки,– координаты точки.

Следствие:
Если
– середина отрезка

,
где
и,
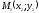
то(1.4) (т.к.).

Например.
Даны точки
и.
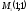
Найти координаты точки,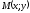
которая в два раза ближе к,
чем к

Решение:
Искомая точка
делит
отрезок

в
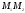
отношении
так как,
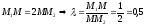
тогда,,
получили

.

Полярные координаты

Наиболее
важной после прямоугольной системы
координат является полярная система
координат. Она состоит из некоторой
точки
,
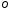
называемойполюсом,
и исходящего из нее луча
–полярной
оси.
Кроме того, задается единица масштаба
для измерения длин отрезков.

Пусть
задана полярная система координат и
пусть
– произвольная точка плоскости. Пусть
–
расстояние от точки

до
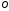
точки
;– угол, на который нужно повернуть
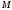
полярную ось для совмещения с лучом.

Полярными
координатами точки
называются числаи.
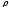
При этом числосчитается первой координатой и называетсяполярным
радиусом,
число
– второй координатой и называетсяполярным
углом.

Обозначается
.
Полярный радиус может иметь любое
неотрицательное значение:.
Обычно считают, что полярный угол
изменяется в следующих пределах:.
Однако в ряде случаев приходится
определять углы, отсчитываемые от
полярной оси по часовой стрелке.

Связь между полярными координатами точки и ее прямоугольными координатами.

Будем
считать, что начало прямоугольной
системы координат находится в полюсе,
а положительная полуось абсцисс совпадает
с полярной осью.

Пусть
– в прямоугольной системе координат и– в полярной системе координат. Определен– прямоугольный треугольник с.
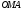
Тогда(1.5).
Эти формулы выражают прямоугольные
координаты через полярные.

С
другой стороны, по теореме Пифагора
и

(1.6)
– эти формулы, выражают полярные
координаты через прямоугольные.

Заметим,
что формула
определяет два значения полярного угла,
так как.
Из этих двух значений углавыбирают тот, при котором удовлетворяются
равенства.

Например,
найдем полярные координаты точки
..или,
т.к.I
четверти.

Пример
1:
Найти точку, симметричную точке

относительно
биссектрисы первого координатного
угла.

Решение:

Проведем
через точку А
прямую l₁,
перпендикулярную биссектрисе l
первого координатного угла. Пусть
.
На прямой
l₁
отложим отрезок
СА₁,
равный
отрезку
АС.
Прямоугольные треугольники
АСО
и
А₁СО
равны
между собой (по двум катетам). Отсюда
следует, что |ОА|
= |OA₁|.
Треугольники
ADO
и
ОЕА₁
также равны между собой (по гипотенузе
и острому углу). Заключаем, что
|AD|
= |ОЕ|
= 4,
|OD| = |EA₁|
=
2, т.е. точка имеет координаты х
= 4, у = -2,
т.е. А₁(4;-2).

Отметим,
что имеет место общее утверждение: точка
A₁,
симметричная точке

относительно биссектрисы первого и
третьего координатных углов, имеет
координаты
,
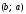
то есть.

Пример
2:
Найти точку, в которой прямая, проходящая
через точки
и
,
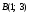
пересечет ось
Ох.

Решение:

Координаты
искомой точки
С
есть (x;
0). А так как точки
А,
В и
С
лежат на одной прямой, то должно
выполняться условие (x₂-x₁)(y₃-y₁)-(x₃-x₁)(y₂-y₁)=0
(формула (1.2), площадь треугольника ABC
равна
нулю!), где

–
координаты точки А,
– точкиВ,
– точкиС.
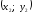
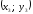
Получаем
,
т.е.,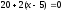
,
.
Следовательно, точка
С
имеет координаты
,,
т.е..

Пример
3: В
полярной системе координат заданы точки
,.
Найти:
а)
расстояние между точками

и
;
б)
площадь треугольника
ОМ₁М₂
(О
– полюс).

Решение:

а)
Воспользуемся формулами (1.1) и (1.5):

,

то
есть,
.

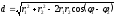
б)
пользуясь формулой для площади
треугольника со сторонами
а
и
b
и углом
между ними (),
находим площадь треугольника
ОМ₁М₂.
.

Треугольник является одной из самых простых фигур, которая часто встречается школьникам в задачах по геометрии. В свою очередь, биссектриса представляет собой важный элемент, характеризующий тот или иной угол. Решение геометрических проблем с участием этих объектов требует наличия определенных знаний. Чтобы уметь составлять по координатам вершин уравнение биссектрисы треугольника, необходимо понимать выражения для прямых линий.

Прямая на плоскости

Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:

На плоскости, где достаточно двух координат для описания любых геометрических объектов.

В трехмерном пространстве, где любая точка имеет три координаты.

Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:

Общий. Он также называется универсальным. Прямая представляет собой следующую математическую запись: A*x + B*y + C = 0. Здесь A, B, C — числовые коэффициенты, x и y — переменные, являющиеся координатами. Сразу нужно отметить, что эта форма представления прямой используется для составления уравнения биссектрисы угла. Для удобства геометрического изображения общую форму записи часто представляют в виде y = f (x). Нужно понимать, что указанной форме в пространстве соответствует не прямая, а плоскость.

Канонический или уравнение в отрезках. Имеет оно такой вид: y/p + x/q = 1. Здесь p, q — это координаты, в которых прямая пересекает оси y и x, соответственно, поэтому удобно ее изображать в координатной системе.

Векторный. Это один из важных типов представления прямой как на плоскости, так и в пространстве. По сути, он является исходным представлением, из которого можно получить все остальные. Математически он записывается так: (x, y) = (x0, y0) + α*(v1, v2). Где (x0, y0) — координаты произвольной точки, которая лежит на прямой, (v1, v2) — направляющий вектор, он параллелен заданной прямой, α — произвольное число, параметр.

Параметрический. Этот тип представляет собой систему уравнений, которую удобно использовать во время преобразования одного вида прямой в другой. Представляет он собой следующую математическую запись: x = x0 + α*v1; y = y0 + α*v2. Несложно понять, что, выражая параметр α, можно получить уравнения общего вида и в отрезках. Объединяя же систему уравнений в одно выражение, получается векторная форма записи прямой.

Делящая пополам угол линия

Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.

Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.

Способы построения

В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:

С помощью транспортира. Для этого следует измерить заданный угол в градусах, разделить его пополам. Полученное значение отметить в виде точки. Затем соединить вершину угла и поставленную точку внутри него. Получится искомый элемент.

С использованием циркуля и линейки. Эти инструменты еще проще применять для построения биссектрисы, чем транспортир. Сначала необходимо установить в вершину угла ножку циркуля и отметить дугами пересечение окружности со сторонами. Затем, в точки пересечения поставить ножку циркуля и провести две окружности. Соединив две точки их пересечения одной прямой, можно получить биссектрису.

Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.

В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.

Основные свойства

Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.

Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.

Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.

В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:

DB/DC = AB/AC.

Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.

Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:

L (A) = 2/(b+c)*(b*c*p*(p-a))^0,5.

Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.

Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.

Уравнение биссектрисы треугольника

Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.

В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):

Сначала требуется определить уравнения двух сторон угла по их координатам. Это легко сделать в векторной форме, а затем, преобразовать ее в выражение общего типа.

Далее, необходимо найти уравнение биссектрис первого координатного угла, прировняв расстояния от ее точек до соответствующей стороны. Рабочая формула имеет вид: |A1*x + B1*y + C|/(A1 ² + B1 ² )^0,5 = |A2*x + B2*y + C|/(A2 ² + B2 ² )^0,5. Следует обратить внимание на наличие двух различных решений этого равенства, поскольку в числителе стоит модульное выражение. Два полученных уравнения говорят о наличии взаимно перпендикулярных биссектрис для углов треугольника внутреннего и внешнего.

Для внутреннего угла искомое уравнение можно найти, если определить точку пересечения соответствующей прямой с противоположной исходному углу стороной треугольника. Та точка, сумма расстояний от которой до концов отрезка будет равна длине стороны, принадлежит искомой биссектрисе.

Пример решения задачи

Пусть, треугольник задан координатами A (1, -1), B (0, -2), C (3,0). Следует уравнение биссектрисы найти для угла B и ее длину вычислить.

Сначала нужно написать уравнения прямых для сторон AB и CB, получается:

• AB: (x, y) = (1, -1) + α*(-1, -1) ==> y — x + 2 = 0;
• CB: (x, y) = (3, 0) + α*(-3, -2) ==> 3*y — 2*x + 6 = 0.

Составить уравнения биссектрис можно так:

| y — x + 2 |/(2)^0,5 = | 3*y — 2*x + 6 |/(13)^0,5.

Решение этого уравнения приводит к следующим двум выражениям для взаимно перпендикулярных биссектрис:

• y*(6−3*3 ^0,5) + x*(3*3 ^0,5 −4)+12−6*3 ^0,5 = 0;
• y*(3*3 ^0,5+6) -x*(4+3*3^0,5)+12+6*3 ^0,5 = 0.

Чтобы определить, какая из двух прямых является искомой для треугольника заданного, следует точку пересечения каждой из них со стороной AC найти. Уравнение для AC имеет вид:

x = 2*y + 3.

Подставляя его в каждое из выражений для биссектрис, можно получить две точки пересечения:

• D1 = (-0,2515;-1,6258);
• D2 = (1,556;-0,722).

При этом длина основания AC составляет 2,236 единицы через единичный вектор. Расстояние от точек D1 и D2 до A, C равно:

• D1A = 1,4; D1C = 3,635;
• D2A = 0,621; D2C = 1,614.

Видно, что точка пересечения второй прямой D2 лежит между A и C, поэтому соответствующее ей уравнение биссектрисы является ответом на задачу. Ее длину можно вычислить по формуле для модуля вектора BD2:

BD2 = 2,014 единицы.

Таким образом, для определения в треугольнике биссектрисы уравнения по координатам следует уметь находить векторную форму выражений для прямой по координатам двух точек. Также нужно знать свойства делящей пополам угол линии.

Предыдущая

ГеометрияКак построить высоту треугольника – основные способы

Следующая

ГеометрияКак доказать, что четырехугольник является параллелограммом?

We will learn how to find the equation of the bisector of
the angle which contains the origin.

Algorithm to determine whether the origin lines in the obtuse angle or acute angle between the lines

Let the equation of the two lines be a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0.

To determine whether the origin lines in the acute angles or obtuse angle between the lines we proceed as follows:

Step I: Obtain whether the constant terms c(_{1}) and c(_{2}) in the equations of the two lines are positive or not. Suppose not, make them positive by multiplying both sides of the equations by negative sign.

Step II: Determine the sign of a(_{1})a(_{2}) + b(_{1})b(_{2}).

Step III: If a(_{1})a(_{2})
+ b(_{1})b(_{2}) > 0, then
the origin lies in the obtuse angle and the “ + “ symbol gives the bisector of
the obtuse angle. If a(_{1})a(_{2}) + b(_{1})b(_{2}) < 0, then the origin lies in the acute angle
and the “ Positive (+) “ symbol gives the bisector of the acute angle i.e.,

(frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} +
b_{1}^{2}}}) = + (frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2} +
b_{2}^{2}}})

Solved examples on the equation of the bisector of the angle which contains the origin:

1. Find the equations of the two bisectors of the angles between
the straight lines 3x + 4y + 1 = 0 and 8x – 6y – 3 = 0. Which of the two
bisectors bisects the angle containing the origin?

Solution:

3x + 4y + 1 = 0 ……….. (i)

8x – 6y – 3 = 0 ……….. (ii)  

The equations of the two bisectors of the angles between the
lines (i) and (ii)

(frac{3x + 4y + 1}{sqrt{3^{2} + 4^{2}}}) = +
(frac{8x – 6y – 3}{sqrt{8^{2} + (-6)^{2}}})

⇒ 2 (3x + 4y + 1) = (8x – 6y – 3)

Therefore, the required two bisectors are given by,

6x + 8y + 2 = 8x+ 6y – 3 (taking `+’ sign)

⇒ 2x – 14y = 5

And 6x+ 8y + 2 = – 8x
+ 6y + 3 (taking `-‘ sign)

⇒ 14x + 2y = 1

Since the constant terms in (i) and (ii) are of opposite
signs, hence the bisector which bisects the angle containing the origin is

2 (3x + 4y + 1) = – (8x
– 6y – 3)

⇒ 14x + 2y= 1.

2. For the
straight lines 4x + 3y – 6 = 0 and 5x + 12y + 9 = 0 find the equation of the
bisector of the angle which contains the origin.

Solution:

To find the bisector of the angle between the lines which
contains the origin, we first write down the equations of the given lines in
such a form that the constant terms in the equations of the lines are positive.
The equations of the given lines are

4x + 3y – 6 = 0 ⇒ -4x – 3y + 6 = 0 ……………………. (i)

5x + 12y + 9 = 0 ……………………. (ii)

Now the equation of the bisector of the angle between the
lines which contains the origin is the bisector corresponding to the positive
symbol i.e.,

(frac{-4x – 3y + 6}{sqrt{(-4)^{2} + (-3)^{2}}}) = +
(frac{5x + 12y + 9}{sqrt{5^{2} + 12^{2}}})

⇒ -52x – 39 y + 78 = 25x + 60y + 45

⇒ 7x + 9y – 3 = 0

Form (i) and (ii), we have a1a2 + b1b2 = -20 – 36 = -56
<0.

Therefore, the origin is situated in an acute angle region
and the bisector of this angle is 7x + 9y – 3 = 0.

● The Straight Line

• Straight Line
• Slope of a Straight Line
• Slope of a Line through Two Given Points
• Collinearity of Three Points
• Equation of a Line Parallel to x-axis
• Equation of a Line Parallel to y-axis
• Slope-intercept Form
• Point-slope Form
• Straight line in Two-point Form
• Straight Line in Intercept Form
• Straight Line in Normal Form
• General Form into Slope-intercept Form
• General Form into Intercept Form
• General Form into Normal Form
  
• Point of Intersection of Two Lines
  
• Concurrency of Three Lines
• Angle between Two Straight Lines
• Condition of Parallelism of Lines
• Equation of a Line Parallel to a Line
• Condition of Perpendicularity of Two Lines
• Equation of a Line Perpendicular to a Line
• Identical Straight Lines
• Position of a Point Relative to a Line
• Distance of a Point from a Straight Line
• Equations of the Bisectors of the Angles between Two Straight Lines
• Bisector of the Angle which Contains the Origin
• Straight Line Formulae
• Problems on Straight Lines
• Word Problems on Straight Lines
• Problems on Slope and Intercept