Как провести биссектрису
Умение разделить любой угол биссектрисой нужно не только для того, чтобы получить «пятерку» по математике. Эти знания очень пригодятся строителю, дизайнеру, землемеру и портнихе. В жизни многое надо уметь делить пополам.
Все в школе учили шуточное определение про крысу, которая бегает по углам и делит угол пополам. Звали этого шустрого и умного грызуна Биссектрисой. Не известно, каким образом крыса делила угол, а для начинающих математиков в школьном учебнике «Геометрия» могут быть предложены следующие способы.
Самый простой способ проведения биссектрисы – с использованием прибора для измерения углов. Нужно приложить транспортир к одной стороне угла, совместив точку отсчета с его острием О. Затем замерить величину угла в градусах или радианах и разделить ее на два. Отложить с помощью того же транспортира полученные градусы от одной из сторон и провести прямую линию, которая и станет биссектрисой, до точки начала угла О.
Нужно взять циркуль и развести его ножки на любой произвольный размер (в пределах чертежа). Установив острие в точке начала угла О, начертить дугу, пересекающую лучи, отметив на них две точки. Обозначают их А1 и А2. Затем, устанавливая циркуль поочередно в эти точки, следует провести две окружности одинакового произвольного диаметра (в масштабе чертежа). Точки их пересечения обозначаются С и В. Далее необходимо провести прямую линию через точки О, С и В, которая и будет искомой биссектрисой.
Для того чтобы начертить биссектрису угла с помощью линейки, нужно отложить от точки О на лучах (сторонах) отрезки одинаковой длины и обозначить их точками А и В. Затем следует соединить их прямой линией и с помощью линейки разделить получившийся отрезок пополам, обозначив точку С. Биссектриса получится, если провести прямую через точки С и О.
Если нет измерительных инструментов, можно воспользоваться смекалкой. Достаточно просто начертить угол на кальке или обычной нетолстой бумаге и аккуратно сложить листок так, чтобы лучи угла совместились. Линия сгиба на чертеже и будет искомой биссектрисой.
Угол больше 180 градусов можно разделить биссектрисой такими же способами. Только делить надо будет не его, а прилежащий к нему острый угол, оставшийся от окружности. Продолжение найденной биссектрисы и станет искомой прямой, делящей развернутый угол пополам.
Следует помнить, что в равностороннем треугольнике биссектриса является также медианой и высотой. Поэтому в нем биссектрису можно найти, просто опустив перпендикуляр на противоположную от угла сторону (высота) или разделив эту сторону пополам и соединив точку середины с противоположным углом (медиана).
Видео по теме
При рассмотрении основных составляющих измерения углов, следует изучить исходные геометрические сведения:
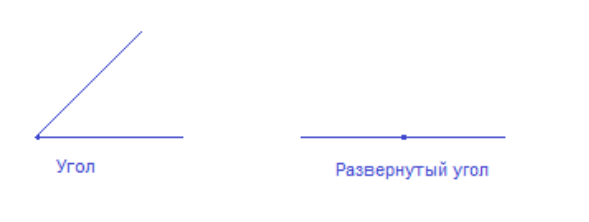
- Угол.
- Развернутый угол, неразвернутый угол.
- Градус, секунда и минута.
- Градусная мера.
- Острый, прямой или тупой.
Геометрическая фигура, которая представляет собой точку — называется вершиной. А исходящие из этой вершины два луча, являются ее сторонами.
Измерение углов производится с помощью градусной меры угла. Углы измеряются таким же способом, как и отрезки, при помощи специальных единиц измерения – градусов.
Определение
Градус — геометрическая единица измерения, представляющая собой угол, который сравнивается с другими углами.
Равенство градуса таково: [frac{1}{180}] от развернутого угла. Исходя из этого, можно понять, что развернутый угол равен 180 градусам, а неразвернутый угол любой меньше 180 градусов.
Чему равна градусная мера угла
Определение
Градусная мера угла – это положительное число, которое показывает сколько раз градус и его части укладываются в данном углу.
А для их измерения используется инструмент – транспортир.
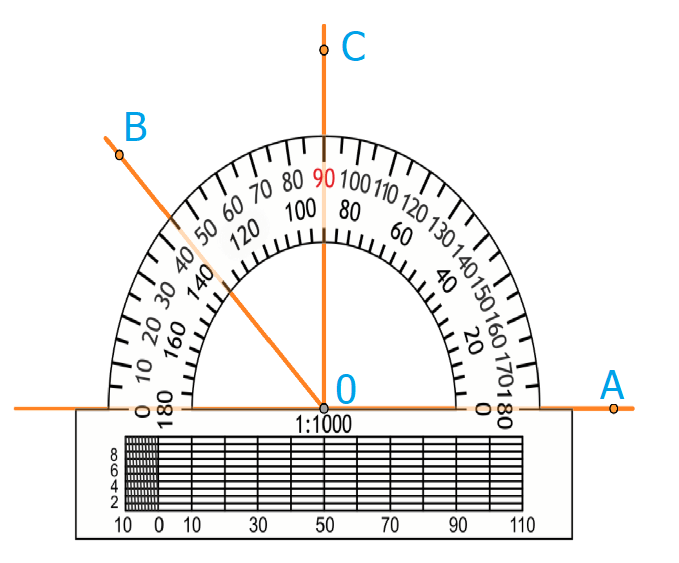
Транспортир используется следующим образом:
- Совместить вершину угла с центром транспортира, при этом одна сторона угла должна пройти по линейке.
- Штрих на шкале транспортира, через который пройдет 2-я сторона, покажет его градусную меру.
Как найти градусную меру угла
На рисунке угол АОВ = 135 градусов. Угол АОС = 90 градусов, угол ВОС = 45 градусов. Градусная мера углов равна сумме углов, на которые он разбит лучом, который проходит между его сторонами.
Отсюда следует, что величина угла AOB на рисунке 1 равна сумме величин углов AOC и [B O C: angle A O B=angle A O C+angle B O C].
Какие бывают названия углов можно понять, разобравшись со следующими обозначениями.
- Минута – 1/60 часть градуса. Обозначается знаком ‘
- Секунда – 1/60 часть минуты. Обозначают знаком»
Например: угол в 65 градусов, 35 минут,18 секунд записывается так: 75°45’28». Если градусная мера у нескольких углов одинаковая, эти углы считаются равными. Сравнить их можно по размерам – больше или меньше. Развернутый и неразвернутый углы.
Нет времени решать самому?
Наши эксперты помогут!
Градусная мера вписанного угла
Градусная мера вписанного угла равняется половине градусной меры дуги, опирающуюся на нее, и половине градусной меры угла, находящегося по центру, которая опирается на эту же дугу.
Вписанный угол равняется половине градусной меры дуги, на которую он опирается.
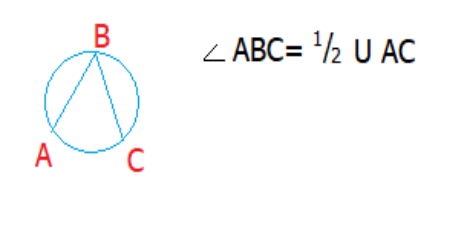
АВ-хорда
ВС-хорда
В-точка окружности.
Углы также различаются несколькими типами:
- Прямыми
- Острыми
- Тупыми
Равность прямого угла составляет — 90 градусов. Острый равен цифре меньше 90 градусов. А тупой же – больше 90 и меньше 180 градусов. В чем же заключается важность умения измерения углов и градусной меры в жизни? Оно пригодится в исследованиях, таких как: астрономия. Например, чтобы вычислить положение различных тел в космосе. Чтобы попрактиковаться, необходимо прочертить несколько неразвернутых углов, отличающихся друг от друга. Также важно потренироваться чертить развернутые. А еще, можно при помощи транспортира поупражняться, задавая случайные цифры, в правильности воспроизведения углов.
Существует еще такое понятие, как, биссектриса.
Определение
Биссектриса— луч, который исходит из вершины этого угла и делит его пополам.
Пример 1. Задача с биссектрисой и развернутым углом.
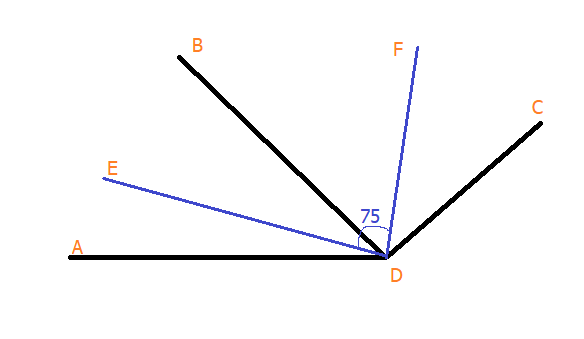
Рис.3 Лучи DЕ и DF – это биссектрисы, которые соответствуют углам ADB и BDC.
Теперь нужно найти угол ADC, при этом угол EDF = 75°
Ответ. Угол EDF имеет по половинке от углов ADB и BDC, это значит, что EDF – это половина самого угла ADC. Теперь получили вычисление угол ADC = 75 умножить на 2 = 150°.
Ответ: 150°
Пример 2. Задача с биссектрисой и прямым углом.
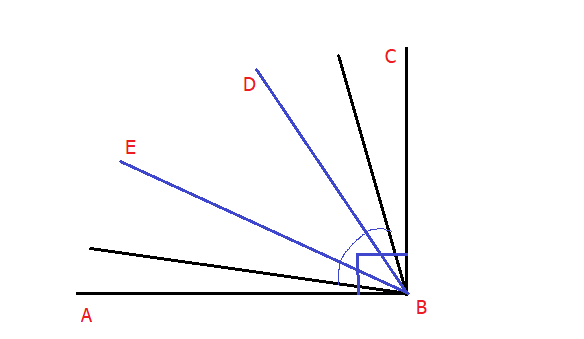
Рисунок 4. По рисунку 4 видно, что угол АВС прямой, а углы ABE EBD DBC равны. Нужно найти угол, который образовали биссектрисы — ABE и DBC.
Решение будет таким: угол АВС прямой, и исходя из этого, можно понять что он равен 90°. Угол ЕВD=90/3=30°. Согласно правилу, углы ABE EBD DBC равны и поэтому каждый из них будет = 30°. Далее видно, что биссектриса любого из трех углов делит любой из этих углов на 2 угла, которые будут равны 15°. Обе половины углов ABE и DBC относятся к углу, который необходимо найти, то можно смело утверждать, что угол, который мы вычисляем, равен 30+15+15=60°.
Решение: 60°
Градусная мера углов треугольника
У любой геометрической фигуры, кроме округлой, имеются углы. При рассмотрении углов треугольника можно увидеть следующее: Сумма углов треугольника всегда равняется 180°. Если рассматривать прямоугольный треугольник, то можно увидеть, что один из углов равен 90°. А сумма двух других углов тоже равняется 90°.
Поэтому, если известно сколько градусов составляет один из острых углов треугольника, второй угол можно найти по формуле:
[angle a=90^{circ}-angle beta]
У прямоугольного треугольника один из углов прямой, соответственно, два других – острые.
Разъяснение острого угла таково: острым углом называется угол, значение которого составляет менее 90 градусов.
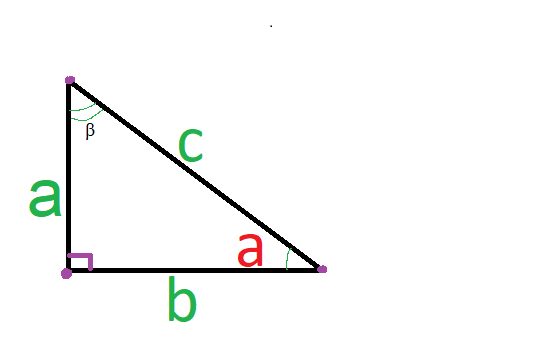
Исходя из вышесказанного, можно отметить, что прямоугольный треугольник — это геометрическая фигура, которая образовалась из трех отрезков. Эти отрезки соединяются между собой тремя точками. Углы у нее все внутренние, а один из них — прямой и равняется 90°. Пример — рисунок 5.
Что такое развёрнутый угол — понятие и обозначение
Определение
Развернутым называют угол со сторонами, лежащей на одной прямой.
Стороны развернутого угла взаимно дополняют друг друга. В результате получается прямая линия. Таким образом, стороны данной геометрической фигуры представляют собой дополнительные лучи. К примеру, на рисунке изображен ∠CDK, который является развернутым. Точка D служит его вершиной, лучи, обозначенные, как DK и DC – сторонами ∠CDK.
Решить задачу, в которой требуется начертить развернутый угол достаточно просто. Необходимо нарисовать прямую линию и поставить на ней отметку в виде точки, которая будет являться вершиной. Существует другой способ. В начале на плоскости отмечают произвольную точку. Данная отметка будет принята за вершину угла. Если через нее прочертить прямую линию, то получится развернутый угол. Схематично оба способа представлены на рисунке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определить, является ли угол развернутым, тупым или острым можно с помощью ряда признаков.
Основные свойства развернутого угла:
- Стороны геометрической фигуры являются антипараллельными и складываются в прямую линию.
- Развернутый угол в любом случае, независимо от способа начертания, будет составлять 180 градусов.
- Если соединить вместе пару смежных углов, то полученная фигура будет выглядеть, как развернутый угол.
- В случае, когда соединяют пару развернутых углов, в результате получают полный угол в 360 градусов, который равен сумме этих углов.
- Прямой угол является половиной развернутого угла.
Геометрические фигуры с развернутыми углами
В геометрии производя некоторые манипуляции с развернутыми углами, можно получить новые фигуры. К примеру, если такую геометрическую фигуру разделить лучом на два угла, то полученные углы называют смежными. Такие элементы изображены на рисунке.
∠ABD в данном случае является развернутым углом, а ВС представляет собой луч. Таким образом, углы ∠ABС и ∠CBD — смежные углы.
С помощью биссектрисы можно разделить представленную фигуру на два прямых угла. Наглядно данный метод получения геометрических фигур продемонстрирован на рисунке.
Так, согласно изображению, KF является биссектрисой развернутого ∠MKP. Полученные углы, ∠MKF и ∠FKP представляют собой прямые углы.
Какова градусная мера развернутого угла (сколько радиан)
Как и любой другой, развернутый угол можно измерить. Градусная величина геометрической фигуры будет составлять (180^{0}). Известно, что в данной единице меры укладывается 3,1415926… радиан. Так как длинные числа не всегда удобно использовать в расчетах, как правило, это число обозначают буквой π. Таким образом, можно записать следующее справедливое обозначение:
(180^{0}approx 3,14) радиан.
Точное отношение будет иметь следующий вид:
(180^{0}=pi) радиан.
Примеры решения задач с развернутыми углами
Задача №1
Развернутый угол разделили с помощью луча на две части, которые являются аналогичными геометрическими фигурами. Градусные меры этих элементов относятся, как 1:4. Требуется найти полученные углы.
Решение
Следует обозначить искомые фигуры, как α и β. Предположим, что х является коэффициентом пропорциональности, тогда справедливы равенства:
α = х
β = 4х
Зная, что развернутый угол равен 180 градусам, что является суммой градусных мер углов, на которые он разбит с помощью луча, проходящего между его сторонами. Данное утверждение вытекает из свойств этой геометрической фигуры. Можно записать следующую формулу:
(x+4x=180^{0}Rightarrow 5x=180^{0})
Исходя из этого, можно определить углы:
(x=alpha =36^{0})
(beta =4x=4*36^{0}=144^{0})
Ответ: после разделения развернутого угла на две части один угол будет равен (36^{0}) второй ставит (144^{0})
Задача 2
С помощью луча ОС развернутый угол, обозначенный, как АОВ, делят на два угла АОС и ВОС таким образом, что градусная мера угла АОС больше на 30 градусов, чем градусная мера угла ВОС. Требуется найти углы АОС и ВОС.
Решение
Условия задачи следует представить на рисунке:
Допустим, что ∠BOC = x, тогда, согласно условию задачи, получим следующее равенство:
∠AOC=(x+30)
Известно, что образованные углы являются смежными. Таким образом, в сумме эти углы будут составлять (180^{0})
∠AOC+∠BOC=180
В результате уравнение приобретает следующий вид:
(x+x+30=180Rightarrow 2x=150Rightarrow x^{0}=75^{0})
∠BOC=75, откуда следует:
∠AOC=(x+30)=105
Ответ: угол (BOC=75^{0}) угол (AOC=105^{0})
Урок 2. Развернутый угол. Смежные углы
Гипермаркет знаний>>Математика>>Математика 4 класс>> Урок 2. Развернутый угол. Смежные углы

1. Раскрась цветным карандашом угол, на который раскрылся веер. Что ты замечаешь?

Угол, стороны которого образуют прямую, называют развернутым углом.

Любой луч, проведенный из вершины развернутого угла, делит его на 2 угла. У них одна сторона общая, а две другие составляют прямую. Такие углы называют смежными.
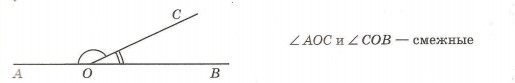
Биссектриса развернутого угла делит его на 2 прямых угла. Значит, биссектрису развернутого угла можно построить с помощью чертежного угольника.

Любой другой луч, проведенный из вершины развернутого угла, делит его на два угла, один из которых острый (меньше прямого), а другой — тупой (больше прямого).
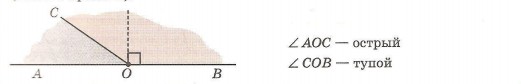
2. Какой угол (острый или тупой) образуют часовая и минутная стрелки на циферблате часов в б ч, 14 ч, 15 ч 25 мин, 22 ч 15 мин?
3. а) Начерти на листе бумаги прямую MN и отметь на ней точку О. Сколько развернутых углов образовалось?
б) Разрежь лист по прямой MN и построй перегибанием биссектрису одного из развернутых углов. Назови все признаки образовавшихся углов. Являются ли эти углы смежными?
в) На модели второго развернутого угла проведи луч ОК с началом в точке О. Прочитай получившиеся углы и назови их признаки. Являются ли они смежными?
4. Построй из палочек или карандашей модели:
а) острого угла; б) прямого угла;
в) тупого угла; г) развернутого угла;
д) смежных углов.
Найди разные виды углов в окружающей обстановке.
5. а) Прочитай название углов на рисунке. На глаз определи их вид и затем проверь с помощью чертежного угольника. Можно ли сравнить эти углы без непосредственного наложения? Сделай записи.
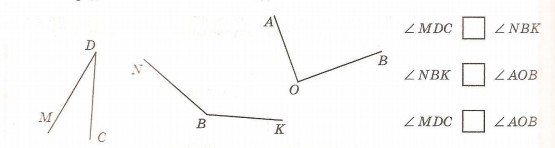
б) На каждом рисунке сделай дополнительные построения так, чтобы получились смежные углы.
6. Являются ли углы 1 и 2 на рисунке смежными? Почему?
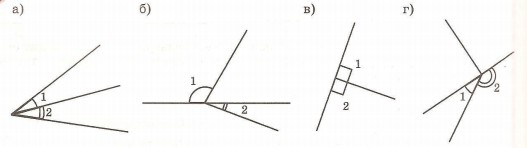
Какие из этих углов являются прямыми, острыми, тупыми?
7. 3апиши множество острых, множество прямых и множество тупых углов на рисунке. Есть ли среди данных фигур прямоугольники?
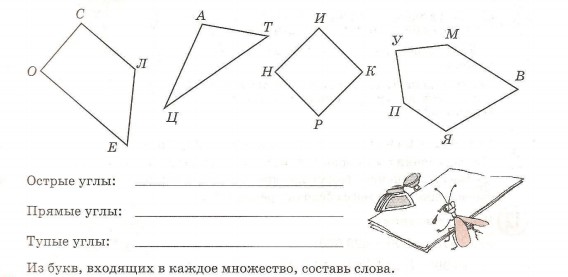
8. Расшифруй название города, который в третьем тысячелетии до нашей эры был столицей Древнего Египта.
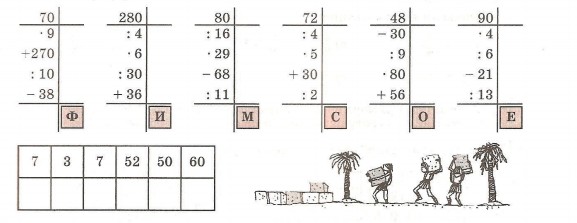
9. Как найти число по его части, выраженной дробью? Найди число, если:

Почему в первых двух случаях число оказалось больше своей части, а в двух других — меньше?
Расположи ответы примеров в порядке убывания, и ты узнаешь название столицы Египта в первом тысячелетии до нашей эры.
10. Объем бидона равен 4 л, что составляет ![]() объема канистры и 2% объема бочки.
объема канистры и 2% объема бочки.
а) На сколько больше жидкости вмещает бочка, чем бидон и канистра, взятые вместе?
б) Во сколько раз объем бочки больше объема бидона?
в) Сколько канистр можно налить из бочки, наполненной до краев? Сколько жидкости еще останется?
11. Белочка, зайчонок и олененок сделали лодку грузоподъемностью 30 кг. Масса белочки составляет 6 % от массы зайчонка, а масса зайчонка равна ![]() массы олененка. Могут ли они отправиться в путешествие по реке на своей лодке, если масса белочки равна 180 г?
массы олененка. Могут ли они отправиться в путешествие по реке на своей лодке, если масса белочки равна 180 г?
12. Реши уравнения:
а) а • 948 – 6390 = 429 690;
б) 273 996 : b + 15 764 = 16 151;
в) (50 – x) : 7 + 195 = 40 • 5;
г) (270 : y – 2) • 30 = 7 • 120.
13. Верны ли высказывания:
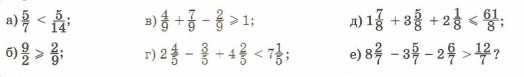
14. Основанием прямоугольного параллелепипеда служит квадрат со стороной 13 см. Найди высоту параллелепипеда, если его объем 1352 см3
15. Вставь в “окошки” пропущенные цифры и сделай проверку:

16*. В большой и дружной семье все мужчины носят одну фамилию и разница в возрасте между любым отцом и сыном составляет 22 года. Правнука зовут Игорь Петрович. Его деда зовут Митрофан Тимофеевич. Как звали в детстве главу семьи и сколько ему лет, если Сереже, сыну Игоря, исполнилось 3 года? Сколько лет Петру Митрофановичу?

Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 3. – М.: Издательство “Ювента”, 2005, – 64 с.: ил.
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Содержание:
- Определение развернутого угла
- Примеры решения задач с развернутыми углами
Определение развернутого угла
Определение
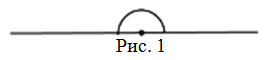
Развернутый угол – это угол,
стороны которого составляют прямую (рис. 1).
Градусная мера развернутого угла равна $180^{circ}$.
Любой луч, проведенный из вершины развернутого угла, делит его на два угла. Полученные в результате углы имеют
одну общую сторону, а две другие составляют прямую. Такие углы называются смежными.
Биссектриса развернутого угла делит его на два
прямых угла.
Если произвольный луч, проведенный из вершины развернутого угла, не является биссектрисой,
то он делит развернутый угол на два, один из которых острый (меньше прямого), а другой – тупой (больше прямого)
Примеры решения задач с развернутыми углами
Пример
Задание. Развернутый угол разделен лучом на два угла,
градусные меры которых относятся как 1:4.
Найдите полученные углы.
Решение. Обозначим искомые углы как
$alpha$ и
$beta$ . Пусть
$x$ – коэффициент пропорциональности, тогда
$alpha = x$, а соответственно
$beta = 4x$ . Так как градусная мера развернутого угла равна
$180^{circ}$ и согласно свойствам угла, что градусная мера
угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами, то делаем вывод, что
$$x+4 x=180^{circ} Rightarrow 5 x=180^{circ}$$
Отсюда находим:
$x=alpha=36^{circ}$ и $beta=4 x=4 cdot 36^{circ}=144^{circ}$
Ответ. $36^{circ}$ и $144^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Луч
$OC$ делит развернутый угол
$AOB$ на два угла
$AOC$ и
$BOC$ так, что угол
$AOC$ на
$30^{circ}$ больше угла
$BOC$ . Найти углы
$AOC$ и
$BOC$ .
Решение. Изобразим заданный развернутый угол и проведем луч
$OC$ (рис. 2).
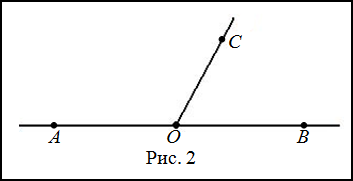
Пусть $angle B O C=x^{circ}$, тогда из условия получаем, что
$angle A O C=(x+30)^{circ}$. Так как эти углы являются
смежными, то их сумма равна
$180^{circ}$, то есть
$$angle A O C+angle B O C=180^{circ}$$
а тогда
$$x+x+30=180 Rightarrow 2 x=150 Rightarrow x^{circ}=angle B O C=75^{circ}$$
Отсюда
$$angle A O C=(x+30)^{circ}=105^{circ}$$
Ответ. $angle A O C=105^{circ}, angle B O C=75^{circ}$
Читать дальше: что такое вертикальные углы.

