Рассмотрим, каким образом может быть найдена биссектриса треугольника по рисунку на клетчатой бумаге.
Задача
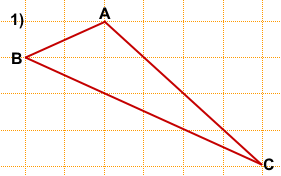
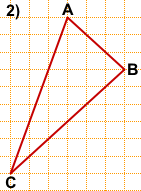
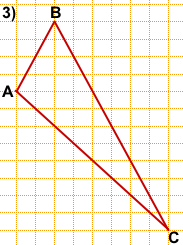
На клетчатой бумаге с размером клетки 1×1 изображен треугольник ABC.
Найдите длину его биссектрисы, проведённой из вершины B.
Решение:
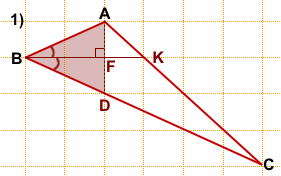 1) Треугольник ABD — равнобедренный с основанием AD.
1) Треугольник ABD — равнобедренный с основанием AD.
Отрезок BF, перпендикулярный основанию AD — высота, медиана и биссектриса треугольника ABD (по свойству равнобедренного треугольника).
Таким образом, ∠ABF=∠DBF.
Продолжим BF до пересечения со стороной AC. На пересечении BF и AC отметим точку K.
BK — биссектриса треугольника ABC, проведённая из вершины B.
Длину BK считаем по клеточкам. BF=3.
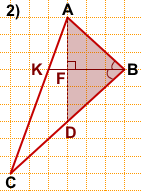
2) Треугольник ABD — равнобедренный с основанием AD.
AF — его высота, медиана и биссектриса.
Продлеваем AF до пересечения со стороной AC в точке K.
BK — искомая биссектриса треугольника ABC.
Длину BK находим по клеточкам: BK=4.
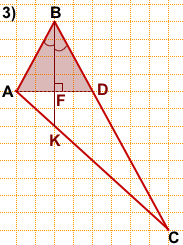 3) В равнобедренном треугольнике ABD
3) В равнобедренном треугольнике ABD
AF — высота, медиана и биссектриса.
Продолжим BF. На пересечении со стороной AC получим точку K.
BK — биссектриса треугольника ABC, длину которой нам нужно найти.
По клеточкам BK=6.
Задания
Версия для печати и копирования в MS Word
Тип 13 № 8090 

i
На клетчатой бумаге с размером клетки 1 × 1 нарисован треугольник ABC. Найдите длину биссектрисы треугольника, выходящей из вершины A.
Спрятать решение
Решение.
Заметим, что биссектриса угла A делит его пополам. Значит, длина биссектрисы треугольника, выходящей из вершины A, равна 5.
Ответ: 5.
Источник: ВПР по математике 7 класса 2020 года. Вариант 11
Спрятать решение
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Задание 3. ЕГЭ. Найти длину биссектрисы треугольника
Рубрика Задание 3, Решаем ЕГЭ по математике Комментарии (0)
Задание. На клетчатой бумаге с размером клетки 1 × 1 изображен треугольник ∆АВС. Найдите длину его биссектрисы, проведенной из вершины В.

Решение:

Проведем DC, тогда треугольник ΔBCD — равнобедренный треугольник с основанием DС. Высота, проведенная из вершины В равнобедренного треугольника ΔBCD, является биссектрисой этого треугольника.
Следовательно, ВК — биссектриса угла В и ВК — биссектриса треугольника ΔАВС. Получим ВК = 6.
Ответ: 6
Понравилось? Нажмите
Алгебра,
вопрос задал 111chocolate111,
8 месяцев назад
Приложения:

parus77:
это равнобедренный треугольник,поэтому биссектриса яв-ся и высотой и медианой,и равна длине двух клеточек,т.е 2.
Ответы на вопрос
Ответил RTA1414
27
Ответ: 2
Объяснение: ΔАВС – равнобедренный ⇒ биссектриса АL⊥ВС.
Проведите биссектрису АL ⊥ ВС. АL=2.
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Информатика,
1 месяц назад
Помогите написать на Паскаль
1)сумма квадратов от 1 до N
S=1+4+9+…n^2…
Математика,
1 месяц назад
Определить цену одной тетради,если за 8 таких тетрадей заплатили 40 руб.
Геометрия,
8 месяцев назад
Помогите срочно пжжж 100 балов за простенькую задачу срочно!
Математика,
8 месяцев назад
Упростите выражение и вычислите его значение: 2) 0,4х – 25у, если х = 2,4, y = 3 помогите пожалуйста …
Химия,
6 лет назад
Пожж нужно срочно решите
Химия 8 класс…
Алгебра,
6 лет назад
Помогите прошуу. Нужно решить уравнение: ctg (3п/2 – x/2) – √3 =0…
Тема 1.
Геометрия на плоскости (планиметрия)
1
.
26
Задачи на клетчатой бумаге
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
геометрия на плоскости (планиметрия)
Решаем задачи
На клетчатой бумаге с размером клетки изображен равносторонний треугольник. Найдите радиус описанной около него
окружности.
Показать ответ и решение
Отметим точки
причем
Центр описанной окружности лежит на пересечении серединных перпендикуляров, в равностороннем
треугольнике серединные перпендикуляры — это и высоты, и медианы, и биссектрисы.
То есть центр описанной окружности лежит на высоте которая также является и медианой. Пусть
— центр этой
окружности (а значит, и точка пересечения медиан треугольника). Так как медианы треугольника точкой пересечения делятся в
отношении считая от вершины, то
откуда
Заметим, что по определению радиус описанной около треугольника окружности — это отрезок, соединяющий центр окружности
с вершиной треугольника, то есть Таким образом, радиус равен 6.
На клетчатой бумаге с размером клетки изображен равнобедренный прямоугольный треугольник. Найдите длину его
биссектрисы, выходящей из вершины прямого угла.
Показать ответ и решение
Так как треугольник равнобедренный, то биссектриса, проведенная к гипотенузе-основанию, является также медианой. По
свойству медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы. У
данного прямоугольного треугольника гипотенуза равна 5. Следовательно, медиана (она же биссектриса) равна
2,5.
На клетчатой бумаге с размером клетки изображен треугольник
Найдите длину средней линии, параллельной стороне
На клетчатой бумаге с клетками размером нарисована трапеция. Найдите её площадь. Ответ дайте в квадратных
миллиметрах.
Показать ответ и решение
Площадь трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции есть
На клетчатой бумаге с размером клетки изображен угол. Найдите тангенс этого угла.
Показать ответ и решение
Проведем перпендикуляр к стороне
Получим прямоугольный треугольник
Из него
На клетчатой бумаге с размером клетки изображен треугольник
Найдите длину его биссектрисы, проведенной из
вершины
Показать ответ и решение
Из рисунка видно, что треугольник равнобедренный (). Следовательно, биссектриса, опущенная из вершины
будет
также являться медианой и высотой. Тогда биссектриса равна 3:
На клетчатой бумаге с размером клетки изображен ромб. Найдите его площадь.
Показать ответ и решение
Проведем диагонали данного ромба:
Площадь ромба равна полупроизведению диагоналей, следовательно,
Показать ответ и решение
Проведем прямую и перпендикуляр
Из рисунка видно, что
Найдите угол Ответ дайте в градусах.
На клетчатой бумаге изображен треугольник Найдите его высоту, опущенную из вершины
если длина стороны
равна 7.
Вершины треугольника лежат в узлах решетки.
На клетчатой бумаге с размером клетки изображен треугольник
Найдите площадь треугольника
где
—
средняя линия, параллельная стороне
Показать ответ и решение
Пусть
По свойству средней линии с коэффициентом подобия, равным 2. Следовательно, их площади относятся как
коэффициент подобия в квадрате, то есть
Высота треугольника опущенная из
равна 2,
Следовательно,
Тогда
На клетчатой бумаге изображен треугольник. Найдите радиус вписанной в него окружности, если сторона одной клетки равна 3.
Показать ответ и решение
Будем искать радиус вписанной окружности по формуле где
— площадь,
— полупериметр.
Заметим, что треугольник равнобедренный:
Так как длина стороны клетки равна 3, то
следовательно,
Тогда
Заметим, что в задачах подобного типа можно вычислять все длины, как будто длина стороны клетки равна 1, а затем
умножать полученный ответ на 3. Если бы длина одной клетки была равна 1, то
и
Тогда после умножения на 3 также получили бы При решении задачи таким способом вычисления будут
легче.
На клетчатой бумаге нарисован круг площадью Найдите площадь
закрашенного сектора.
Показать ответ и решение
Заметим, что закрашенная фигура состоит из двух непересекающихся частей,
равных и
от
круга:
Таким образом, ее площадь равна
Найдите разность площади фигуры 1 и площади фигуры 2.
Показать ответ и решение
Площадь фигуры 1 можно посчитать следующим образом:
Площадь фигуры 2 — следующим образом:
Тогда
Размер клетки Найдите площадь фигуры с вырезанным кругом, выраженную в квадратных сантиметрах.
Показать ответ и решение
Искомая фигура состоит из квадрата без вырезанного круга с центром
и двух половин круга такого же радиуса,
следовательно, площадь искомой фигуры равна площади квадрата
На рисунке изображен треугольник. Найдите угол
На клетчатой бумаге с клетками размером 1 мм 1 мм нарисован невыпуклый
шестиугольник Найдите его площадь. Ответ дайте в квадратных
миллиметрах.
Показать ответ и решение
Дорисуем несколько отрезков как показано на рисунке ниже:
Площадь треугольника равна половине произведения основания на высоту к этому основанию. Площадь треугольника
равна
Площадь треугольника равна
Площадь трапеции равна
Тогда
На клетчатой бумаге с клетками размером 1 мм 1 мм нарисован четырёхугольник. Найдите его площадь. Ответ дайте в
квадратных миллиметрах.
Показать ответ и решение
У данного четырёхугольника две стороны параллельны, а две другие не параллельны, следовательно, это трапеция. Площадь
трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции равна
Найдите радиус окружности, вписанной в треугольник считая стороны квадратных клеток равными 1.
Показать ответ и решение
Так как радиус окружности, вписанной в прямоугольный треугольник, ищется по формуле где
— катеты,
— гипотенуза, то
На клетчатой бумаге с размером клетки изображен угол. Найдите синус
этого угла.
Показать ответ и решение
Продлим одну из сторон тупого угла на отрезок
так, чтобы
Заметим, что все вершины треугольника находятся в узлах решетки,
причем
Тогда
Так как синус острого угла (в прямоугольном треугольнике) — это отношение
противолежащего катета к гипотенузе, то
Угол с тупым углом
— смежные, следовательно, их синусы равны,
значит, синус тупого угла равен также
