Как найти биссектрису треугольника огэ

Здравствуйте, уважаемые читатели. В этой статье рассмотрим простейшие задания по геометрии на применение свойств медианы и биссектрисы в треугольнике.

Что такое медиана треугольника?

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Другими словами, медиана треугольника делит противоположную сторону на два равных отрезка.

Задача №1

В этой задаче длина медианы ВМ является лишней и для решения не используются. Для решения нужно взять длину стороны АС. Чтобы найти АМ нужно, по свойству медианы треугольника, разделить сторону АС на 2 и получим отрезок АМ.

Задача №2

Что такое биссектриса ?

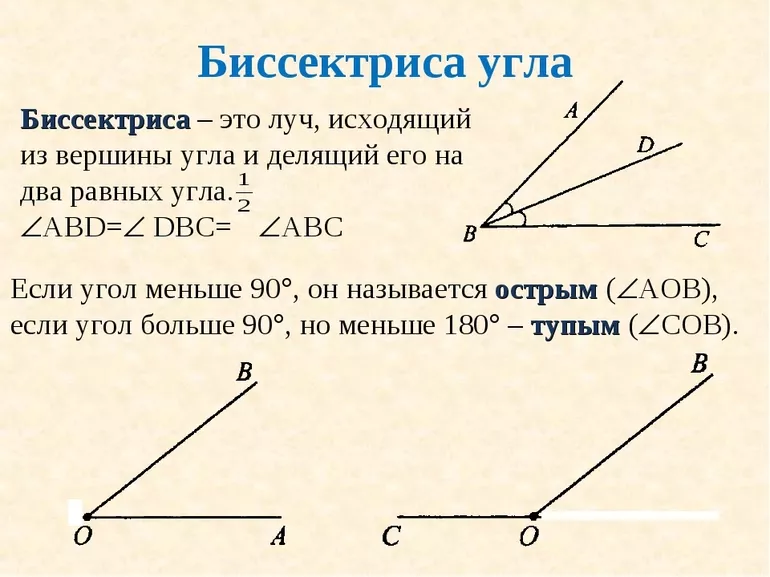
Биссектриса угла – это луч, исходящий из вершины угла и делящий этот угол на два равных.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части.

Теперь решим задачу.

Задача №3

В условии задачи, точка М – середина стороны АВ, значит СМ – медиана. Вспомним свойство медианы в прямоугольном треугольнике проведенной из вершины прямого угла:

Медиана в прямоугольном треугольнике, проведенная из вершины прямого угла к гипотенузе, равна половине гипотенузы (значение гипотенузы делим на 2). Значит для решения задачи этой задачи нам нужно знать только значение отрезок АВ (гипотенузы), а значение отрезка ВС дано лишним.

Задача №4

Так как точка М является серединой АВ (АМ= МВ) и точка N является серединой ВС (BN=NC), то отрезки СМ и AN являются медианами в треугольнике АВС. Для решения этой задачи полезно знать свойство медиан треугольника:

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Решим задачу на части:

Весь отрезок AN = 15, но он поделен точкой О на два отрезка. Один отрезок равен две части, второй отрезок равен одной части.

Задача №5

Здесь представлены на вид 6 разных задач, но если внимательно прочитать, то можно заметить, что они одинаковые. Решить такие задачи можно как по теореме Пифагора, так и с помощью свойства медиан в треугольнике и вписанной окружности.

Для решения этих задач с помощью свойств медиан в треугольнике, вспомним свойство равностороннего треугольника и вписанной окружности в треугольник.

1) В равностороннем треугольнике медианы, биссектрисы и высоты совпадают и пересекаются в одной точке.

2) Центром вписанной окружности в треугольник является точка пересечения биссектрис. Значит в разностороннем треугольнике центром вписанной окружности является пересечение биссектрис, медиан и высот.

3) Свойство медиан в треугольнике: Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Рассмотрим решение такой задачи:

Для нахождения стороны или высоты равностороннего (правильного) треугольника, воспользуемся формулами, которые есть в справочном материале, выдаваемое на экзамене:

Так как в нашей задаче биссектриса равностороннего треугольника является медианой, найдем чему будет равна одна часть, т.е. радиус вписанной окружности:

Аналогично решаются задачи, где дана медиана или высота равностороннего (правильного) треугольника.

Решим второй тип подобной задачи:

Так как биссектриса в равностороннем треугольнике является медианой и высотой, то мы можем найти высоты по формуле

Можно эту задачу решить через свойство медиан треугольника:

Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог

Задания

Версия для печати и копирования в MS Word

Аннотация

   Подготовка учащихся к ГИА должна носить системный характер,
позволяющий в тоге создать у учащихся целостную картину знаний по элементарной
математике.

  Данная работа представляет собой сборник методических материалов
объединяющих, систематизирующих и расширяющих знания учащихся по теме
«Биссектриса треугольника и её свойства». Что поможет проводить системную
подготовку к ГИА.

  В работу вошли материалы школьной программы и материалы,
факутальтивных и элективных курсов по данной теме.

  Работа предназначена для учителей предметников, учащихся старших
классов и репетиторов по математике.

Содержание

1.  
Биссектриса треугольника и некоторые её
свойства:

а) Определение
биссектрисы, биссектрисы треугольника.

б) Основное свойство
биссектрисы треугольника.

в) Точка пересечения
биссектрис треугольника.

     
    г) Лемма о «дважды» биссектрисе.

      
   д) Свойство биссектрисы внешнего угла треугольника.

2.   Задачи,
для которых можно использовать доказанные свойства.

3.  
Решение задач ГИА.

4.  
Заключение и вывод.

Введение

  Геометрия является очень мощным средством развития личности в
самом широком смысле. Этот школьный предмет отличается нежеланием подчиняться
стандартам, нормам, алгоритмам. Целью изучения геометрии, конечно, являются
знания.

  Цель моей работы – помочь ученикам 10-11 классов
систематизировать и углубить знания, научить решать геометрические задачи.

  Задача – это не только умения, это и элемент знания. Ученик
должен ознакомиться с определённым набором достаточно трудных геометрических
задач, научиться решать задачи. Выполняя эту работу, он научиться из большого
объёма информации выбирать и систематизировать нужный материал, который
используется при решении задач. Самое главное поможет более прочно усвоить
теоретический материал, а решение задач разовьёт логическое мышление.

 
Я
хотела бы научить решать задачи по геометрии и помочь в преодолении трудностей
при их решении своим ученикам. Для этого нужно по каждой теме подобрать и
решить определенный блок задач.

  Из обилия
геометрических фигур я выбрала – биссектрису, самую понятную и простую, самую интересную
и удивительную фигуру планиметрии. В геометрии особо можно выделить теорему:
биссектриса треугольника делит его сторону на части, в отношении прилежащих
сторон. Этот факт упрощает решение многих олимпиадных задач и задач государственной
итоговой аттестации. Я подробно исследую этот объект. Сформулирую и докажу
интересующие нас свойства.

  Моя работа
поможет учителям провести системную работу по подготовке учащихся к олимпиадам,
сдаче ГИА и последующей учёбе.

  Материалы
представленные в работе могут быть полезны учителям при организации учебных
занятий, особенно изучении тех типов задач , которые не рассматриваются в
рамках обычной школьной программы, на занятиях школьного математического
кружка.

1. Биссектриса
   треугольника и некоторые её свойства:

а)
Определение биссектрисы, биссектриса треугольника

Определение
биссектрисы угла

Луч,
исходящий из вершины угла и делящий его на два равных угла, называется
биссектрисой угла.

Определение
биссектрисы угла треугольника

Отрезок
биссектрисы угла треугольника, соединяющий вершину треугольника с точкой
противоположной стороны, называется биссектрисой треугольника.

 

б) Основное свойство
биссектрисы треугольника.

Теорема о биссектрисе треугольника

Биссектриса
треугольника делит противоположную сторону на отрезки, пропорциональные
прилежащим сторонам треугольника.

 

Доказательство:

Пусть
АD
– биссектриса треугольника ABC.
Докажем, что BD : AB
= CD
: AC.        

  
ABD
и     ACD
имеют общую высоту AH, поэтому S_ABD :
S_ACD
= BD
: CD.

С
другой стороны, эти же треугольники имеют по равному углу (∠1
= ∠2), поэтому S_ABD :
S_ACD
= (AB
· AD)
: (AC
· AD)
= AB
: AC.
Из двух равенств для отношения площадей получаем

BD
: CD
= AB
: AC,
или BD
: AB
= CD
: AC,
что и требовалось доказать.

в)
Задача 1. В треугольнике ABC сторона 𝐴𝐵
= 𝑐, 𝐵𝐶
= 𝑎, 𝐴𝐶
= 𝑏. В каком отношении
биссектрисы 𝐴𝐾,
𝐵𝐿,
𝐶𝑀
этого треугольника делятся их общей точкой О?

Решение:

AK
биссектриса угла А, треугольника ABC,
АK
= x,
CK
= a
– x,

по
свойству биссектрисы АС : АВ = (а – х) : х, АС = b,
то bx
= c(a–x),

 

bx
+ cx = ac, x = ac : (b + c).

BO
биссектриса
угла
B, треугольника ABK, АK
= x, CK = a – x,

по
свойству
биссектрисы
АO
: OK = AB : BK, AO : OK = c : x = c(b + c) : (ac) = (b + c) : a,  AO : OK =
(b + c) : a. 

Аналогично,
BO : OL = (a + c) : b,  CO : OM = (a + b) : c.

г)
Лемма о «дважды биссектрисе» угла треугольника

Биссектриса
угла треугольника делит пополам угол между радиусом описанной окружности и
высотой, проведенной из вершины того же угла.

 Иными
словами, l_а
(биссектриса угла А) является биссектрисой угла
ОАН₁.

Чтобы
не возникало никаких вопросов, поясню, что такое описанная окружность. Если все
вершины многоугольника лежат на окружности, то окружность называется описанной
около многоугольника, а многоугольник – вписанным в эту окружность.

Биссектриса
l треугольника
АВС является также биссектрисой угла ОАН₁, где О –
центр окружности, описанной около треугольника АВС, АН₁ –
его высота.

Доказательство.

Угол
АОС является центральным, АОС = 2В. Тогда = 90 Но и = 90 (из треугольника ВАН). Поскольку биссектриса lделит угол ВАС
пополам, то, отняв от равных углов CALи  BAL равные части, мы
вновь получим равные углы. Поэтому ∠1
= 2.
Лемма доказана.

д) Свойство
биссектрисы внешнего угла треугольника

 Биссектриса
внешнего угла треугольника делит продолжение противоположной стороны на
отрезки, пропорциональные прилежащим сторонам.

А

Дано: Δ
АВС, BD –
биссектриса ∠ CBF

Доказать: 

Доказательство:   

  1. Проведём CK
параллельно BD

2. ∠CKB
= ∠DBE – соответственные при BD ∥
CK, секущей AF,

2.     ∠DBC
= ∠BCK – накрест лежащие углы при BD ∥
CK, cекущей BC,

3.     ∠CKB = ∠DBE

∠DBC
= ∠BCK   =>
∠CKB = ∠BKC => ⊿ KBC равн6обедренный =>

∠DBC
= DBF  и  BK = BC

4.   

5.    
Задачи, для которых можно
использовать доказанные свойства.

№1.
Докажите, что если биссектрисы треугольника ABC
точкой I
делятся в одном отношении, то ⊿ABC
равносторонний.

Доказательство:

По
условию: , следовательно,  = =  , прибавим к обеим
частям 1, получим  ==, т.е. a
= b
= c. 
Треугольник ABC
равнобедренный.

№2.
В треугольнике АВС через 0 точку пересечения биссектрис проведены
прямые, параллельные сторонам треугольника. Найдите длины отрезков этих прямых,
отсекаемых сторонами треугольника

 

Решение:  

Найдём
отрезок EF.
то , где AL₁=AI+IL₁=
(b+c)+a.

Из
подобия треугольников AEF и
ABC получим
 или ,

EF
= . Остальные отрезки
находятся аналогично.

 №3. В треугольнике АВС
биссектриса AL
и высота ВН пересекаются в точке О. Найти радиус
описанной
вокруг треугольника АВС окружности, если известно, что ВС=4, а ВО:ОН=5:3.

 №4. Биссектрисы BD и CE ∆ABC пересекаются в точке О.
АВ=14, ВС=6, АС=10. Найдите ОD.

 №5.
Биссектриса внутреннего угла В треугольника АВС
рассекает сторону АС на отрезки АК = 5, КС = 7.
На
каком расстоянии от вершин А и С пересечет

продолжение
АС биссектриса внешнего угла В?

6.    
Решение задач ГИА.

№1.
Один из углов треугольника равен 60⁰, O,
J,
H
– соответственно центры описанной, вписанной окружностей и точка пересечения
высот этого треугольника. Доказать, что треугольник OJH
– равнобедренный.

Доказательство:

1)    О
– центр описанной около ⊿ABC окружности,
∠BOC центральный, ∠BAC –
вписанный угол в окружность, они опираются на одну дугу, описанной около ⊿ABC окружности.
∠BOC=2∠BAC,
∠BOC=120⁰.

2)    Н
точка пересечения высот BH₂
и CH₂
⊿ABC,

∠BAC +∠H₁HH₂=180⁰
как углы с взаимно перпендикулярными сторонами =>
∠H₁HH₂
= 120⁰, ∠BНC
= ∠H₁HH₂
как вертикальные,

∠BНC
= 120⁰.

3)  ∠BIC
= 180⁰ –  угол между биссектрисами

∠BIC
=
180⁰
–

4)   ∠BOC=120⁰,
∠BНC
= 120⁰, ∠BIC
=. Поэтому
точки B,
O,
I,
H
лежат на окружности описанной около ⊿
BOC.
Причём, если ∠В > ∠С,
то лучи BH, BI,
BO
пересекают окружность в указанном порядке (если

∠В
<∠С, то BO, BI,
BH пересекают
окружность в таком порядке).

5)    По
свойству «дважды» биссектрисы, биссектриса BI
∠HBO =>

 ∠HBI = ∠OBI вписанные
углы, опирающиеся на равные дуги HI
и IO ⊿HIO
равнобедренный.

№2. (ЕГЭ
2016)

Точка O —центр
окружности, описанной около остроугольного треугольника 

ABC, I —центр
вписанной в него окружности, H —точка пересечения высот.

Известно, что  

а) Докажите, что точка I лежит
на окружности, описанной около треугольника BOC.

б) Найдите угол OIH, если 

Доказательство:

Точка O — центр описанной окружности около
треугольника ABC, поэтому 

 По теореме о сумме углов треугольника

По условию задачи,

тогда , .

Найдём  по теореме о
сумме углов треугольника

=

.  поэтому
точки B, I, O и C лежат на одной окружности, описанной
около

 

б) Найдём BHC: СH₁BH₂ высоты,  H₁ =  H_{2 =} , углы ∠ BAC и ∠H₁HH₂ углы с взаимно перпендикулярными сторонами, т.е.

 ∠H₁HH₂=  ∠BHC =∠ H₁HH= как
вертикальные.  поэтому
точки B, I, O и C лежат на одной окружности, описанной
около  Т.к. ∠BAC= получаем 

В 𝛥Н₂BC, ∠H₂==

Точка О центр описанной окружности, то 𝛥BOC равнобедренный, ∠OBC=.

∠HBC=            

  Биссектриса угла треугольника лежит внутри угла,
образованного радиусом описанной окружности и высотой, исходящими из той же
вершины, поэтому лучи BH, BI и BO пересекают
дугу окружности в указанном на рисунке порядке.

Точки B, O, I и C лежат
на одной окружности, четырехугольник

, т.е. ∠B+∠I=и ∠HIO= 

Ответ: б)
165°.

№3 В треугольнике АВС проведена биссектриса АМ.
Прямая, проходящая через вершину В, перпендикулярно АМ,
пересекает сторону АС в точке N. АВ =
6; ВС = 5; АС = 9.

а) докажите, что биссектриса
угла С делит отрезок МN пополам

б) пусть Р —
точка пересечения биссектрис треугольника АВС. Найдите
отношение АР : РN.

 а) Доказательство:

 Обозначим K точку
пересечения отрезков AM и BN.   

 Треугольник ABN равнобедренный,
так как в нем AK является биссектрисой и высотой.
Следовательно, AK является и медианой, то есть K —
середина BN. Получаем, что AN = AB = 6,
откуда NC = AC − AN = 3.

1)    Рассмотрим треугольник ABC, биссектриса делит
противоположную сторону на отрезки, пропорциональные прилежащим сторонам: BM : MC = AB : AC,
учитывая, что длина BC равна 5, получаем: BM =
2; MC = 3.

2)    В ⊿АВN  АК  биссектриса
и высота ( т. к. AM ⊥ BN ), значит, ⊿ABN равнобедренный и AB = AN = 6. Откуда NC = AC – AN, NC = 3

3)     В треугольнике MNC стороны NC и MC равны,
следовательно, треугольник MNC — равнобедренный, с
основанием MN. Значит, биссектриса угла C также
является медианой и высотой.

 Таким образом, получаем, что биссектриса угла С делит
отрезок MN пополам.

б) Решение:

Р
точка пересечения биссектрис 𝛥ABC,
т.е. AP
: PM=

AP : PM.

б) Решение одиннадцатиклассников:

 Рассмотрим ⊿ PMN: отрезок PO перпендикулярен
прямой MN и делит её пополам, следовательно,
треугольник PMN — равнобедренный с основанием MN.
Значит, PM = PN и
отношение AP : PN = AP : PM.

 В
треугольнике AMC отрезок CP —биссектриса, поэтому 

AP : PM = AC : MC =
3 : 1.

Ответ: 3
: 1

№4. (Аналогичная задаче № 2,
ЕГЭ 2016)

Точка O —центр окружности, описанной около
остроугольного треугольника 

ABC, I —центр
вписанной в него окружности, H —точка пересечения высот.

Известно, что  

а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.

б) Найдите угол OHI, если 

Задачи на
применение свойств биссектрисы

№ 1. В
треугольнике АВС биссектриса AL и высота ВН
пересекаются в точке О. Найти радиус описанной вокруг
треугольника АВС окружности, если известно, что ВС=4, а ВО:ОН=5:3.

№2. Биссектриса
внутреннего угла В треугольника АВС рассекает сторону АС
на отрезки АК = 5, КС = 7. На каком расстоянии от вершин А
и С пересечет продолжение АС биссектриса внешнего угла В?

№ 3. Дан ΔАВС, в
котором угол В равен 30⁰, АВ = 4, ВС = 6. Биссектриса угла
В пересекает сторону АС в точке D. Определите
площадь треугольника ABD.

№ 4. Одна из
биссектрис треугольника делится точкой пересечения биссектрис

в отношении 3:2,
считая от вершины. Найдите периметр треугольника, если длина стороны
треугольника, к которой эта биссектриса проведена, равна 12.

№ 5. В
равнобедренном треугольнике АBC с основанием BС проведена
биссектриса ВE. Известно, что АЕ = 20 и   СE = 10. Найдите
BE.

№ 6. В
равнобедренном треугольнике АBC с основанием BС проведена
биссектриса ВE. Известно, что АЕ = 20 и   СE = 10. Найдите
BE.

№ 7. Определить
площадь треугольника, если две его стороны равны 35 см и 14 см, а биссектриса
угла между ними содержит 12 см.

№ 8. Биссектрисы
BD и CE ∆ABC
пересекаются в точке О. АВ=14, ВС=6, АС=10. Найдите
ОD.

№ 9. В треугольнике ABC через точку пересечения биссектрис углов В и С. Провести прямую,
параллельную стороне ВС. Доказать, что MN = BM + CN.

 

№ 10. В треугольнике АВС проведена биссектриса угла В,
пересекающая сторону АС в точке D. Через точку D проведена прямая, параллельная стороне ВС и пересекающая сторону
АВ в точке F.
Доказать, что DF = BF.

Заключение.

  Решение задач – это всегда поиск, приводящий к выявлению
каких-то зависимостей и отношений, и в этом процессе помогают знания приёмов и
методов , интуиция и догадки. «В решении любой задачи присутствует крупица
открытия» Д.Пойя.

Изучение математики осуществляется в основном в процессе решения
задач. Умение решать сложные задачи различными способами является одним из
критериев глубины освоения материала. Какой бы путь решения ни был выбран,
успешность его использования зависит от знания определений, свойств, от знания
теории и умения их применять.

 
Выполняя работу, ученики научатся из большого объема информации выбирать и
систематизировать нужный материал, который используют при решении задач.

 Самое
главное работа поможет более прочно усвоить теоретического материала, а решение
задач разовьёт логическое мышление. На примере данной теоремы ученики учатся применять
ранее изученный материал. Учатся анализировать и оценивать недостатки данного
способа, выбирая наиболее удачный из них.  .

 
Материал работы – основа для решения задач в старшей школе. Эти
задачи содержатся в задачах ГИА. Таким образом тема актуальна, перспективна и
имеет продолжение.

  В работе проведены исследования свойств биссектрисы.
Сформулированы и решены базовые задачи, результатом которых являются формулы и
отношения,  используемые при решении других, более сложных задач.

   Решено несколько сложных задач ЕГЭ. Рассмотрены основные
подходы к их решению. Приобретен хороший опыт решения планиметрических задач.
Таким образом, цель работы достигнута.

  Практическая ценность данного
исследования заключается в использовании результатов для более качественной
подготовке к олимпиадам, математическим конкурсам и ГИА.

Список используемой литературы

1.     Л.С.
Атанасян. Геометрия 7-9. М.: Просвещение, 2018

2.     Научно-теоретический
и методический журнал «Математика в школе», М.: Школьная пресса, 4 выпуск, 2008

3.     В.Б.
Полонский, Е.М. Рабинович, М.С. Якир. Геометрия: Задачник к школьному курсу. –
М.: АСТ-ПРЕСС: Магистр-S. 1998

4.     Л.С.
Атанасян, В. Ф. Бутузов, С.Б. Кадомцев и др. Геометрия. Дополнительные главы к
учебнику: Учебное пособие для учащихся школ и классов с углубленным изучением
математики. – М.: Вита-Пресс, 20004

5.     М.Я.
Выгодский. Справочник по элементарной математике- Государственное издательство
физико-математической литературы, Москва,1963

Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:
На плоскости, где достаточно двух координат для описания любых геометрических объектов.

Прямая на плоскости

Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:

1. На плоскости, где достаточно двух координат для описания любых геометрических объектов.
2. В трехмерном пространстве, где любая точка имеет три координаты.

Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:

1. Общий. Он также называется универсальным. Прямая представляет собой следующую математическую запись: A*x + B*y + C = 0. Здесь A, B, C — числовые коэффициенты, x и y — переменные, являющиеся координатами. Сразу нужно отметить, что эта форма представления прямой используется для составления уравнения биссектрисы угла. Для удобства геометрического изображения общую форму записи часто представляют в виде y = f (x). Нужно понимать, что указанной форме в пространстве соответствует не прямая, а плоскость.
2. Канонический или уравнение в отрезках. Имеет оно такой вид: y/p + x/q = 1. Здесь p, q — это координаты, в которых прямая пересекает оси y и x, соответственно, поэтому удобно ее изображать в координатной системе.
3. Векторный. Это один из важных типов представления прямой как на плоскости, так и в пространстве. По сути, он является исходным представлением, из которого можно получить все остальные. Математически он записывается так: (x, y) = (x0, y0) + α*(v1, v2). Где (x0, y0) — координаты произвольной точки, которая лежит на прямой, (v1, v2) — направляющий вектор, он параллелен заданной прямой, α — произвольное число, параметр.
4. Параметрический. Этот тип представляет собой систему уравнений, которую удобно использовать во время преобразования одного вида прямой в другой. Представляет он собой следующую математическую запись: x = x0 + α*v1; y = y0 + α*v2. Несложно понять, что, выражая параметр α, можно получить уравнения общего вида и в отрезках. Объединяя же систему уравнений в одно выражение, получается векторная форма записи прямой.

Продолжение следует…

Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность

Делящая пополам угол линия

Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.

Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.

Способы построения

В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:

1. С помощью транспортира. Для этого следует измерить заданный угол в градусах, разделить его пополам. Полученное значение отметить в виде точки. Затем соединить вершину угла и поставленную точку внутри него. Получится искомый элемент.
2. С использованием циркуля и линейки. Эти инструменты еще проще применять для построения биссектрисы, чем транспортир. Сначала необходимо установить в вершину угла ножку циркуля и отметить дугами пересечение окружности со сторонами. Затем, в точки пересечения поставить ножку циркуля и провести две окружности. Соединив две точки их пересечения одной прямой, можно получить биссектрису.

Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.

В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.

Основные свойства

Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.

Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.

Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.

В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:

DB/DC = AB/AC.

Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.

Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:

L (A) = 2/(b+c)*(b*c*p*(p-a))^0,5.

Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.

Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.

Уравнение биссектрисы треугольника

Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.

В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):

1. Сначала требуется определить уравнения двух сторон угла по их координатам. Это легко сделать в векторной форме, а затем, преобразовать ее в выражение общего типа.
2. Далее, необходимо найти уравнение биссектрис первого координатного угла, прировняв расстояния от ее точек до соответствующей стороны. Рабочая формула имеет вид: |A1*x + B1*y + C|/(A1 2 + B1 2 )^0,5 = |A2*x + B2*y + C|/(A2 2 + B2 2 )^0,5. Следует обратить внимание на наличие двух различных решений этого равенства, поскольку в числителе стоит модульное выражение. Два полученных уравнения говорят о наличии взаимно перпендикулярных биссектрис для углов треугольника внутреннего и внешнего.
3. Для внутреннего угла искомое уравнение можно найти, если определить точку пересечения соответствующей прямой с противоположной исходному углу стороной треугольника. Та точка, сумма расстояний от которой до концов отрезка будет равна длине стороны, принадлежит искомой биссектрисе.

( 1 оценка, среднее 5 из 5 )

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Содержание страницы:

Определение треугольника

Треугольник – многоугольник с тремя сторонами и тремя углами.

Угол ∠ A – угол, образованный сторонами A B и A C и противолежащий стороне B C .

Угол ∠ B – угол, образованный сторонами B A и B C и противолежащий стороне A C .

Угол ∠ C – угол, образованный сторонами C B и C A и противолежащий стороне A B .

Виды треугольников

Треугольник остроугольный, если все три угла в треугольнике острые.

Треугольник прямоугольный, если у него один из углов прямой ( = 90 ° ) .

Треугольник тупоугольный, если у него один из углов тупой.

Примеры:

Основные свойства треугольника:

• Против большей стороны лежит больший угол.
• Против равных сторон лежат равные углы.
• Сумма углов в треугольнике равна 180 ° .
• Если продолжить одну из сторон треугольника, например, A C , и взять на продолжении стороны точку D , образуется внешний угол ∠ B C D к исходному углу ∠ A C B .

  

  Внешний угол равен сумме двух внутренних углов, не смежных с ним. ∠ B C D = 180 ° − ∠ A C B ∠ B C D = ∠ A + ∠ B

• Неравенство треугольника: любая из сторон треугольника меньше суммы двух других сторон и больше их разности.

Отрезки в треугольнике

Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.

Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.

Свойства биссектрис треугольника:

• Биссектриса угла – геометрическое место точек, равноудаленных от сторон угла.
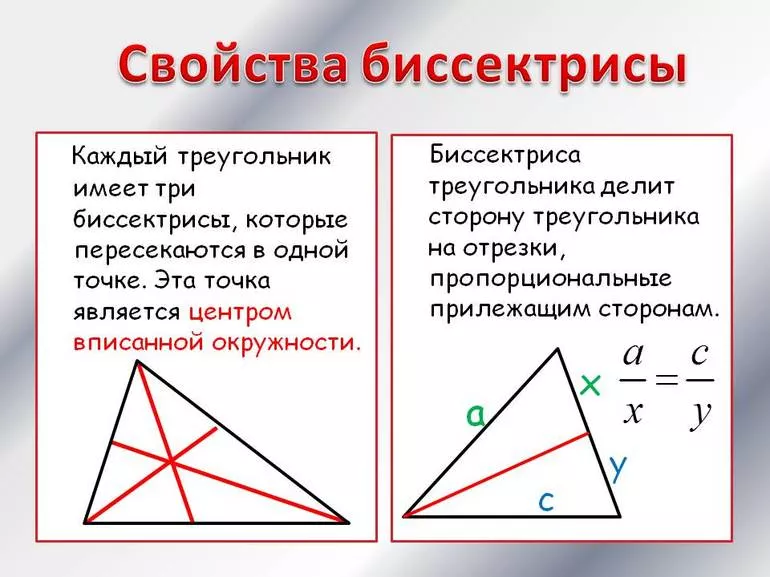
• Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:

  

  a b = m n

• Биссектрисы пересекаются в одной точке. Точка пересечения биссектрис – центр вписанной в треугольник окружности.

Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Свойства медиан треугольника:

• Медиана разбивает треугольник на два равновеликих треугольника (два треугольника, имеющих одинаковую площадь).
• Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.

  

• Три медианы, проведенные в одном треугольнике, разбивают его на шесть равновеликих треугольников.

  

  S 1 = S 2 = S 3 = S 4 = S 5 = S 6

Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.

Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.

Пример:

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.

m = a 2

Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.

Площадь треугольника

Площадь произвольного треугольника можно найти следующими способами:

• Полупроизведение стороны на высоту, проведенную к этой стороне.

  

  S = 1 2 a ⋅ h a

• Полупроизведение двух сторон на синус угла между ними.

  

  S = 1 2 a ⋅ b ⋅ sin α

• По формуле Герона.

  

  S = p ( p − a ) ( p − b ) ( p − c ) p = a + b + c 2

Равнобедренный треугольник

Равнобедренным называется треугольник, у которого две стороны равны.

Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.

Свойства равноберенного треугольника:

• В равнобедренном треугольнике углы при основании равны.
• В равнобедренном треугольнике медиана, высота и биссектриса, проведенные к основанию, совпадают.

Равносторонний треугольник

Равносторонним называется треугольник, у которого все стороны и все углы равны.

Площадь равностороннего треугольника находится по формуле S = a 2 3 4

Высота равностороннего треугольника находится по формуле h = a 3 2

Прямоугольный треугольник

Треугольник называется прямоугольным, если у него один из углов равен 90 ° .

Свойства прямоугольного треугольника:

• Сумма двух острых углов треугольника равна 90 ° .
• Катет, лежащий напротив угла в 30 ° , равен половине гипотенузы.
• Если катет равен половине гипотенузы, он лежит напротив угла в 30 ° .

  

  a = c 2 c = 2 ⋅ a

• Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.

  

  m = c 2

• Пропорциональные отрезки в прямоугольном треугольнике

  

  a = m ⋅ c b = n ⋅ c h = m ⋅ n

Теорема Пифагора

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

c 2 = a 2 + b 2

У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:

S = 1 2 a ⋅ b

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с треугольниками

Скачать домашнее задание к уроку 3.