|
Как построить с помощью циркуля высоту треугольника, медиану, биссектрису ?
Что касается высоты треугольника, то её можно построить, например, так: строим окружность циркулем, далееотмечаем точки пересечения окружностей с треугольником по прямой от его стороны, из этих точек проводим по окружности ещё. Находим точку пересечения и проводим прямую от вершины:
ВG – здесь высота. Что касается бссектрисы, то она делит угол в трегольнике пополам, поэтому можно рассмотреть бессиктрису для угла, аналогично она строитя будет и в треугольнике, а вот алгоритм построения:
Бессиктриса здесь АD. Теперь о медиане: В таком заданном треугольнике как АВС будем строить медиану, которая падает из угла С в треугольнике на сторону АВ. Сут в том, что потребуется при помощи циркуля разбить сторону АВ на две равные части:
CD здесь медиана. автор вопроса выбрал этот ответ лучшим
127771 3 года назад Итак, рассмотрим по порядку. Для начала построим медиану с помощью циркуля. У нас есть треугольника АСВ. Из точки А и В построим две окружности с таким радиусом, чтобы окружности пересеклись. Точки пересечения окружностей назовем Р и Q. Теперь проводим прямую через эти точки. Прямая пересекается с АВ в точке D. CD будет медианой.
Теперь рассмотрим, как найти высоту в треугольнике. У нас треугольник АВС. Строим зеленую окружность, которая пересекает сторону АС в точке D и E (на рисунке точка Е не лежит на стороне АС). Далее строим синие окружности центром которых будут точки Е и D. ВQ здесь будет высотой.
Осталось рассмотреть только, как построить биссектрису. У нас есть треугольник АСВ. Из точки А строим окружность, которая будет пресекаться со стороной АС в точке N и со стороной АВ в точке М. Далее строим из точки N и М радиусом NM. Внутри треугольника окружности пересекутся в точке Х. Проводим прямую через точки АХ. АZ будет биссектрисой.
Nelli4ka 5 лет назад Давайте начнем с высоты. Ниже дан для примера треугольник. Берем циркуль, проводим две окружности:
Далее нам нужно начертить зеркальный вариант искомого треугольника (я начертила его красным цветом). Останется только соединить вершины нашего нового треугольника с точкой С (отмечено желтым цветом). Высота треугольника найдена, все лишнее можно стереть.
Строим медиану. Также нужно начертить циркулем две окружности, но сделать это нужно так, чтобы они в итоге заходили друг на друга. То есть делайте радиус таким, чтобы он был больше половины отрезка АВ. Наши окружности пересеклись друг с другом в двух точках, соединяем их. Точка М – это середина АВ, нужно соединить ее с вершиной С – это и есть медиана.
Теперь осталась биссектриса (чертила сама, не судите строго).
Итак, чертим произвольную окружность с вершиной В в качестве ее центра (предположим, что именно биссектрису угла АВС нужно найти). Окружность пересеклась со сторонами в точках М и Р. Из этих двух точек нужно провести еще две окружности. Радиус этих окружностей для наглядности сделайте чуть больше, чем отрезок МВ и ВР соответственно. Эти две последние окружности пересеклись в точке Е. Соедините ее с В – вот и биссектриса.
Galina7v7 6 лет назад Для того ,чтобы в треугольнике АВС провести из вершины В высоту ВН на стороны АС , то для этого нужно восстановить перпендикуляр к стороне АС из вершины В.И самый простой способ для этого это провести медиану в равнобедренном треугольнике АВС1 , где АВ = ВС1.Для получения точки С1 проведём циркулем из т.В засечку на АС раствором циркуля АВ=ВС1.с помощью циркуля найдём середину АС ,проведя раствором циркуля более половины АС1 полуокружности из точек А и С1 до пересечения.Места пересечек соединим , и получим на АС1 точку Н -середину АС1. Соединим точку Н с В , получим высоту треугольника ВН. Построение медианы.Для этого находим середину стороны АС описанным выше способом.Получив точку М – середину АС , соединим М с В , МВ- медиана. Биссектриса.Для построения нужно поделить угол <ABC пополам известным способом , проведя из т.В раствором циркуля АВ= ВС1 , и найдя точку М1 – середину АС1 ,соединим М1 с точкой В .ВМ1 – биссектриса <ABC.Продолжив ВМ1 до АС получим точку L1 , BL1 биссектриса в треугольнике АВС.
Бархатные лапки 3 года назад Вспоминаем, что такое медиана, биссектриса и высота треугольника. Прежде всего это отрезки или лучи. Медиана соединяет любую вершину с точкой-серединой стороны противоположной. Биссектриса делит угол пополам, это луч. Высота:
Мы имеем треугольник, циркуль и по умолчанию линейку, которой и будем чертить прямые. Для построения медианы, мы делим отрезок пополам, для этого проводим полуокружности одного радиуса из двух точек, соединяем точки пересечения их и находим точку пересечения со стороной треугольника, соединяем с противоположной вершиной. Готово. Чтобы построить биссектрису, мы из угла чертим окружность, из 2-х точек пересечения со сторонами чертим еще 2 дуги или полуокружности одного радиуса, получаем точку пересечения. Эту точку соединяем с вершиной угла. На рисунке АЕ соединяем и получаем биссектрису.
Построим высоту следующим образом. Чертим окружности АС и СВ, где радиусы равны сторонам, находим точку пересечения и соединяем. СМ – высота.
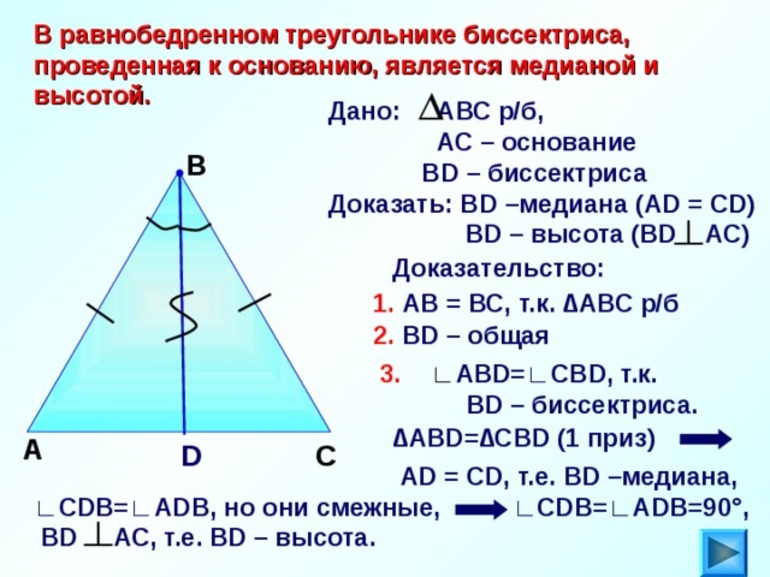
Треугольник АВС. В – вершина. АС – основание. Высота. Нужно из точки А провести дугу радиусом АВ, из точки С дугу радиусом ВС. Получится точка пересечения за пределами треугольника. Через эту точку из точки В чертим линию до основания. Биссектриса. Чертим дугу с центром В так, чтобы дуга пересекла стороны АВ и ВС, на сторонах получаем две промежуточные точки, из которых проводим две дуги с равным радиусом, который несколько больше половины основания, соединяем точку пересечения с В. Медиана. Из точек А и С проводим две дуги радиусом несколько больше половины основания, две полученные точки соединяем, линия пересекает основание в середине. Среднюю точку соединяем с точкой В. Такие действия можно провести с любым углом и стороной. Сахарный имбирь 5 лет назад Одного циркуля мало, нужна еще линейка. Теперь представим, что перед нами треугольник с вершиной А и основанием ВС. Берем циркуль, устанавливаем его иглой в точке В. Проходим круг так, чтобы он проходил через вершину А. Тоже самое делаем с точкой С. Получаем две окружности, которые пересекаются в двух точках, соединяем их линией. Так мы получили высоту. Так мы найдем медиану:
Проводим также из точек В и С две окружности (обозначения взяты из предыдущего примера), но уже произвольные, так, чтобы они также пересекались в двух местах, точки пересечения соединяем, берем ту точку, которая у нас таким образом образовалась на основании (на рисунке это точка М), соединяем ее с вершиной. Биссектриса находится путем черчения трех окружностей: первая – с центром в вершине А, вторые две – с центром в тех точках, которые получились в результате черчения первой окружности. Нижнюю точку пересечения этих двух окружностей соединяем с вершиной.
Бекки Шарп 5 лет назад Самое простое – это медиана. Находим с помощью циркуля середину противоположной стороны угла. Равным раствором циркуля, чуть большим предполагаемой середины рисуем окружности из вершин треугольника. Соединяем две точки пересечения окружностей. Пересечение этой линии со стороной – середина. Соединяем вершину треугольника с сединой противоположной стороны и получает медиану. Биссектриса. Из вершины треугольника чертим две окружности одинакового раствора циркуля, из точек пересечения со сторонами треугольника чертим еще две окружности и соединяем вершину с точкой пересечения последних окружностей. А вот найти высоту задача поинтересней. Я бы ее решила так. Построила бы внутри нашего треугольника равнобедренный и соединила бы середину стороны нового треугольника с вершиной из которой нам надо опустить высоту.
Марина Вологда 3 года назад Мне очень сложно правильно словами описать весь процесс построения, поэтому легче к словам прикрепить схему, как это делается. 1) Рисуем медиану. Для этого из точки А произвольным радиусом рисуем окружность. Не меняя радиуса строим окружность из точки С. Соединяем две точки пересечений окружностей. Их той точки, где пересекает отрезок треугольника, рисуем биссектрису.
2) Рисуем биссектрису. Из точки А треугольника рисуем циркулем произвольный радиус. Отмечаем точки окружности пересечения окружности с треугольником. Теперь в одной из этих точек строим снова циркулем произвольную окружность. Из другой точки рисуем окружность этим же радиусом. Смотрим пересечение этих двух окружностей. Рисуем биссектрису.
3) А вот так можно при помощи циркуля рисовать высоту. Grigi Funny 1 минуту назад Можно сделать всё намного проще (при помощи этого способа можно найти и высоту, и медиану, и биссектрису одновременно). Итак, для начала чертим горизонтальную прямую, отмечаем на ней две точки на любом расстоянии (пускай это будут точки D и B). После, от точки D делаем при помощи циркуля окружность с радиусом равный отрезку DB и уже потом от точки B проводим точно такой же радиус. По итогу у нас есть две точки соприкосновения двух окружностей, проведём через них прямую линию и получим серединный перпендикуляр (то есть линию которая будет делить наш отрезок DB на две равные части, а также в точке соприкосновения, которую мы назовём точкой А, будет угол равный 90 градусов). Теперь от недавно найденной точки А, проведём окружность с радиусом равный отрезку DА и увидим 4 новые точки соприкосновения, но нам нужна только верхняя вертикальная точка соприкосновения, назовём это точку С. Теперь можно провести при помощи циркуля от точки С ещё одну окружность равную отрезку СА и не меняя радиус циркуля, провести от точки В точно такую же, последнюю окружность. И если сделать всё правильно то получим совершенно новые, две точки соприкосновения двух радиусов, можно их соединить между собой (линия, которую мы только что провели должна идеально проходить через точку А), а так же можно соединить две точки С и В, получив прямоугольный треугольник САВ, где точка А будет равна 90 градусов. Теперь можно переходить на последний этап, а именно, назвать новую точку пересечения с отрезком СВ, пускай это точка будет называться О. И наконец, мы всё сделали, а именно: 1.Получили прямоугольный треугольник САВ, где угол А будет равен 90 градусов; 2.Получили отрезок АО, который будет являться и медианой, и биссектрисой, и высотой треугольника САВ.
Алиса в Стране 3 года назад Вспоминаем, что такое высота, это перпендикуляр, проходящий через один из углов треугольника и противоположную сторону. Построить с помощью циркуля очень легко, смотрим на рисунок:
Проводим циркулем окружность с радиусом равным стороне ВС и центром в точке В, а затем окружность с радиусом АС и центром в точке А. Две точки пересечения этих окружностей как раз и лежать на нужной нам высоте, проводим высоту через эти две точки. В построении медианы тоже нет ничего сложного, нам нужно просто определить с помощью циркуля середину стороны треугольника АВ:
Для этого чертим две окружности, одну с центром в точке А, другую с центром в точке В, окружности должны иметь такие радиусы, чтобы находить друг на друга, две точки пересечения дадут нам прямую, которая пересечет сторону треугольника АВ в ее середине, пусть это будет точка М. Теперь соединяем эту точку М и вершину треугольника С, получим медиану СМ. А теперь построим биссектрису треугольника, то есть биссектрису одного из углов треугольника, смотрим на рисунок:
Сначала чертим окружность с центром в вершине угла А произвольного радиуса, точки пересечения этой окружности со сторонами треугольника, прилегающими к вершине А обозначим – В и С. Теперь чертим окружности с центрами в этих точках – В и С, они пересекутся в точке D? через эту точку и вершину угла А и проводим биссектрису угла А. Знаете ответ? |
Процесс построения
Биссектриса (лат. bisectio) представляет собой геометрическое место точек внутри угла (острый, прямой или тупой), которые одинаково удалены от обеих его сторон.
Для её построения нужно подготовить различные школьные принадлежности и выполнить несколько простых действий.
Подготовительный этап
Чтобы быстро найти биссектрису треугольника с помощью циркуля, нужно провести тщательную подготовку. Она заключается в поиске школьных принадлежностей, которые будут использоваться при построении.
Необходимые предметы:

- простой карандаш;
- линейка;
- ластик;
- циркуль;
- лист бумаги.
Порядок действий
Нарисовать луч, разделяющий пополам угол, можно при помощи транспортира. Однако если этой школьной принадлежности нет в наличии, заменить её сможет обыкновенный циркуль.
Быстрый способ:
- На листе бумаги рисуют 2 пересекающиеся линии.
- Чтобы построить биссектрису данного угла, в его вершину ставят ножку циркуля и чертят окружность произвольного радиуса.
- Отмечают точками места пересечения сторон угла с окружностью.
- На них поочерёдно ставят циркуль и, не меняя радиус, рисуют 2 дуги.
- Находят и отмечают место их пересечения.
- Стирают дуги ластиком, чтобы они не мешали дальнейшей работе.
- С помощью линейки и простого карандаша проводят искомый отрезок, соединяющий вершину угла с точкой пересечения дуг.
С помощью циркуля можно легко найти биссектрису треугольника (всякого). Для этого понадобится стандартный набор школьных принадлежностей и наличие базовых знаний геометрии.
Порядок действий:
- Любым известным способом вписывают окружность в треугольник.
- С помощью карандаша и линейки из её центра проводят линии к каждой вершине.
- Полученные отрезки станут частью искомого луча.
Альтернативный вариант
Если у ученика нет циркуля, то начертить луч, разделяющий угол пополам, можно и без этой школьной принадлежности. Для работы понадобится линейка, карандаш и транспортир.
Правильная последовательность действий:
- Нулевое значение на шкале прикладывают к вершине.
- Совмещают линейку транспортира с одним из лучей и определяют величину угла.
- Полученное значение делят пополам.
- Затем заново прикладывают транспортир и откладывают величину, полученную в результате расчётов.
- Через эту точку и вершину проводят отрезок, который будет являться искомым лучом.
Полезные советы
В некоторых случаях для нахождения не нужно использовать транспортир и циркуль. Это возможно только тогда, когда нужно определить расположение биссектрисы в треугольнике.
Полезные рекомендации:
- Биссектриса всегда разделяет противолежащую сторону треугольника в отношении, равном пропорции 2 других сторон геометрической фигуры.
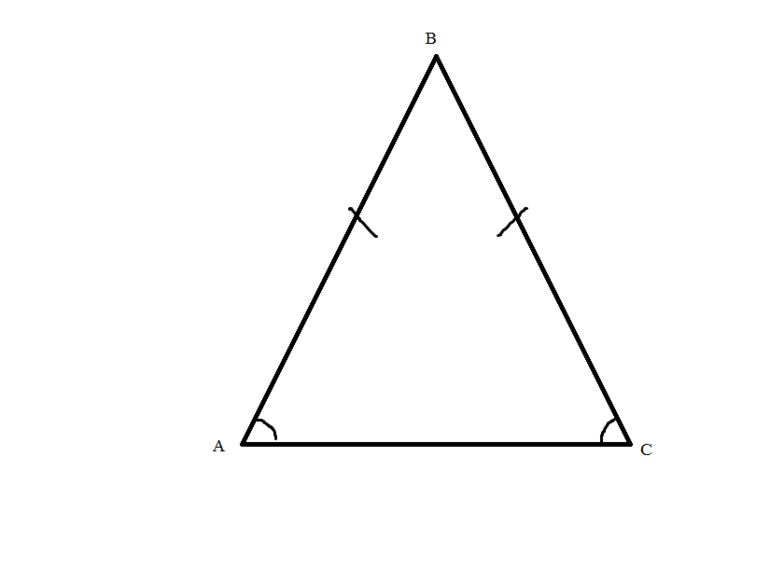
- В равнобедренном треугольнике биссектрисы всегда пересекаются под прямым углом.
- Если треугольник равносторонний, то все биссектрисы будут параллельны противоположным сторонам. При этом длина образованных отрезков будет одинаковой.
Построить биссектрису угла с помощью циркуля сможет даже двоечник. Для этого ему понадобится минимум времени, знаний и усилий. Подробно изучив порядок действий, каждый учащийся сможет легко поделить любой угол пополам и объяснить этот процесс одноклассникам.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Построения циркулем и линейкой
- Построение биссектрисы угла
Пример:
Построить биссектрису данного угла.
Дано:  А.
А.
Построить: биссектрису  А.
А.
Решение:
Произвольно строим с помощью линейки  А.
А.

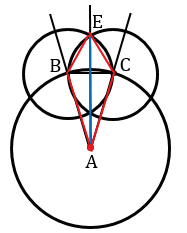
С помощью циркуля строим окружность произвольного радиуса с центром в вершине  А.
А.
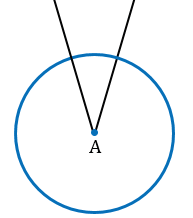
Точки пересечения данной окружности со сторонами  А обозначим В и С.
А обозначим В и С.
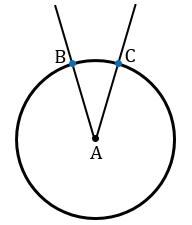
Теперь проведем две окружности одинакового радиуса ВС с центрами в точках В и С.
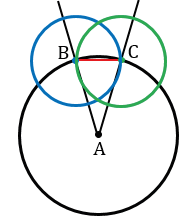
В зависимости от длины ВС, получим одну или две точки пересечения данных окружностей внутри  А. Ту точку, которая лежит внутри угла обозначают буквой и проводят через нее луч с началом в точке А. В нашем случае, получилось две точки пересечения данных окружностей, которые лежат внутри
А. Ту точку, которая лежит внутри угла обозначают буквой и проводят через нее луч с началом в точке А. В нашем случае, получилось две точки пересечения данных окружностей, которые лежат внутри  А. Обозначаем одну из них Е и проводим с помощью линейки луч АЕ.
А. Обозначаем одну из них Е и проводим с помощью линейки луч АЕ.
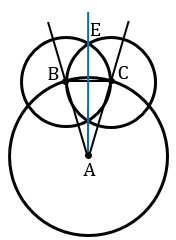
Докажем, что луч АЕ является биссектрисой данного  А. Рассмотрим треугольники АВЕ и АСЕ.
А. Рассмотрим треугольники АВЕ и АСЕ.
В данных треугольниках АВ = АС как радиусы окружности с центром в точке А, ВЕ = СЕ по построению, АЕ – общая, следовательно, 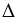 АВЕ =
АВЕ =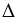 АСЕ по 3 признаку равенства треугольников, откуда следует, что
АСЕ по 3 признаку равенства треугольников, откуда следует, что  ВАЕ =
ВАЕ = САЕ, т.е луч АЕ – биссектриса данного
САЕ, т.е луч АЕ – биссектриса данного  А. Что и требовалось доказать.
А. Что и требовалось доказать.
Замечание:
- С помощью циркуля и линейки можно разделить данный угол на два равных угла, для этого нужно провести его биссектрису.
- С помощью циркуля и линейки можно разделить данный угол на четыре равных угла, для этого нужно разделить угол пополам (на два равных угла), а затем каждую половину разделить пополам еще раз.
- С помощью циркуля и линейки нельзя разделить данный угол на три равных угла (задача о трисекции угла).
Советуем посмотреть:
Построение угла, равного данному
Построение перпендикулярных прямых
Построение середины отрезка
Среднее пропорциональное
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 155,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 19,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 289,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 317,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 357,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 358,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 362,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 586,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 701,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1100,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Как построить биссектрису треугольника
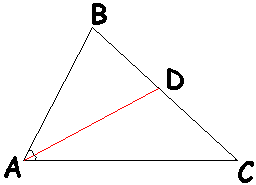
Треугольник и его построения имеют важное значение в начальной геометрии. Одно из построений треугольника – биссектриса – представляет собой прямой отрезок, исходящий из одной вершины треугольника и соединяющийся с точкой на противолежащем ребре. При этом биссектриса делит пополам угол данной вершины. В общем случае построение биссектрисы треугольника сводится к проведению биссектрисы угла конкретной вершины. Это построение выполняется с помощью транспортира. Однако построение биссектрисы равнобедренного и правильного треугольников можно провести с учетом их геометрических свойств без дополнительных инструментов.
Вам понадобится
- Транспортир, линейка
Инструкция
Постройте заданный треугольник. Возьмите транспортир и измерьте угол вершины, из которой необходимо провести биссектрису. Поделите данный угол пополам.
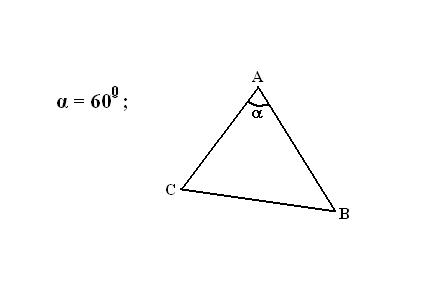
Отмерьте от стороны треугольника, прилегающей к данной вершине, высчитанный угол. Поставьте точку, обозначающую половину угла вершины.
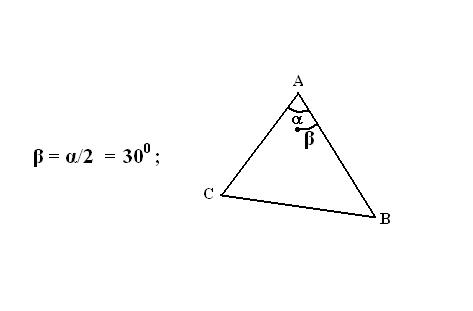
Проведите через вершину и отмеченную точку прямую линию так, чтобы она ограничивалась вершиной с одной стороны и противолежащей стороной треугольника с другой. Биссектриса треугольника построена.
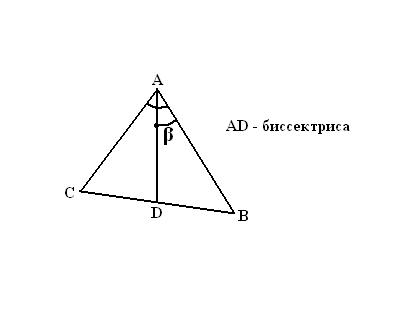
Если заданный треугольник является равнобедренным или правильным, то есть у него
равны две или три стороны, то его биссектриса, согласно свойству треугольника, будет являться также и медианой. А, следовательно, противолежащая сторона будет делиться биссектрисой пополам.
Измерьте линейкой противолежащую строну треугольника, куда будет стремиться биссектриса. Поделите данную строну пополам и поставьте в середине стороны точку.
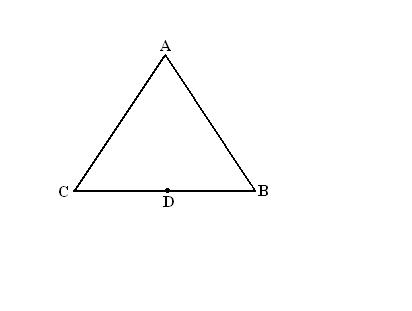
Проведите прямую линию, проходящую через построенную точку и противолежащую вершину. Это и будет биссектриса треугольника.
Источники:
- Медианы, биссектрисы и высоты треугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
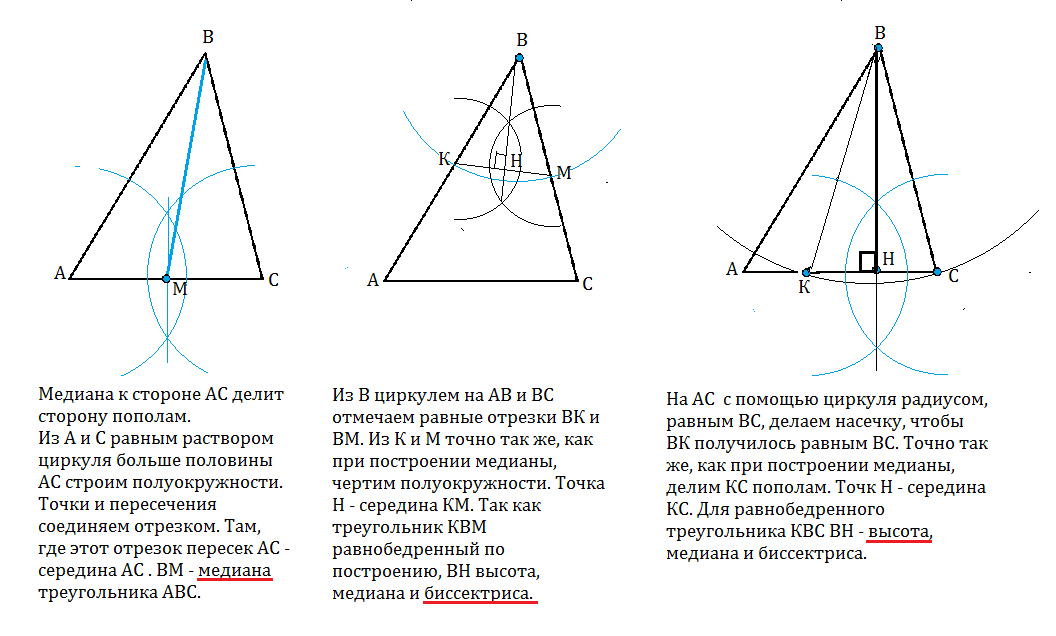
Биссектриса, высота и медиана с помощью циркуля. Объясняем, как построить в треугольниках с помощью циркуля биссектрису, медиану и высоту.
Биссектриса, высота, медиана с помощью циркуля
Посмотреть еще в категории: Треугольник
- Равносторонний треугольник
- Прямоугольный треугольник
- Высота, медиана, биссектриса треугольника
- Средняя линия треугольника
- Четыре замечательные точки треугольника
- Таблица синуса, косинуса, тангенса и котангенса



























