Элементы треугольника. Биссектриса
Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.
Свойства биссектрисы
1. Биссектриса треугольника делит угол пополам.
2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()
3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.
4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.
Некоторые формулы, связанные с биссектрисой треугольника
(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,
Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.
Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1
Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Медианы, биссектрисы и высоты треугольника
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы продолжим рассмотрение элементов треугольника – медиан, биссектрис и высот треугольника.
Вначале дадим определение медианы треугольника и рассмотрим три медианы треугольника. Дадим определение биссектрисы треугольника и рассмотрим три биссектрисы треугольника. Дадим определение высоты треугольника и рассмотрим высоты в произвольном треугольнике и в тупом треугольнике. Далее решим ряд задач с использованием этих элементов.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
[spoiler title=”источники:”]
http://interneturok.ru/lesson/geometry/7-klass/treugolnikib/mediany-bissektrisy-i-vysoty-treugolnika
[/spoiler]
Содержание:
- § 1 Теорема о биссектрисе угла
- § 2 Теорема о серединном перпендикуляре к отрезку
- § 3 Теорема о пересечении высот теугольника
§ 1 Теорема о биссектрисе угла
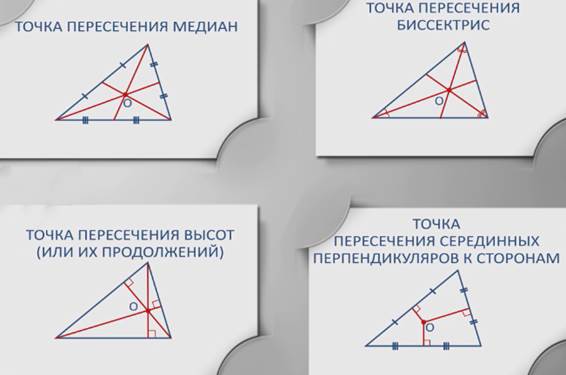
С любым треугольником в геометрии связаны четыре точки:
1) точка пересечения медиан;
2) точка пересечения биссектрис;
3) точка пересечения высот (или их продолжений);
4) точка пересечения серединных перпендикуляров к сторонам.
Эти четыре точки называют замечательными точками треугольника.
В этом уроке рассмотрим и докажем теоремы, следствия из этих теорем, связанные с замечательными точками треугольника, и рассмотрим их применение при решении задач.
Познакомимся сначала с теоремой о биссектрисе угла.
Теорема:
Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
Обратно:
Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.
Докажем эти утверждения.
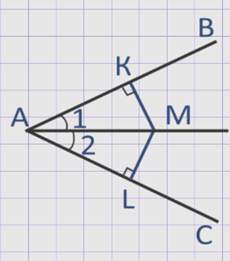
Дано:
∠ВАС, АМ – биссектриса, МК и МL перпендикулярны к прямым АВ и АС.
Доказать:
МК = МL
Доказательство:
Рассмотрим прямоугольные треугольники АКМ и АLМ.
Они равны по гипотенузе и острому углу (АМ – общая сторона, ∠1 = ∠2 , так как по условию АМ – биссектриса).
Из равенства треугольников следует МК = МL.
Теперь докажем обратное утверждение.
Дано:
∠ВАС, точка М лежит внутри угла и равноудалена от сторон угла АВ и АС.
Доказать:
луч АМ – биссектриса ∠ВАС.
Доказательство:
Проведем перпендикуляры МК и МL к прямым АВ и АС.
Прямоугольные треугольники АМК и АМL равны по гипотенузе и катету (АМ – общая гипотенуза, МК = МL по условию).
Следовательно, ∠1 = ∠2, это означает, что луч АМ – биссектриса ∠ВАС.
Теорема доказана.
Из утверждения теоремы следует еще одно утверждение.
Следствие: биссектрисы треугольника пересекаются в одной точке.
§ 2 Теорема о серединном перпендикуляре к отрезку
Перейдем к теореме о серединном перпендикуляре к отрезку.
Но сначала дадим определение.
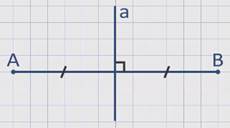
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
На рисунке прямая а является серединным перпендикуляром к отрезку АВ.
Теорема:
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Обратно:
Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Дано:
АВ – отрезок, прямая m – серединный перпендикуляр к отрезку АВ, точка О – середина этого отрезка.
М – произвольная точка прямой m.
Доказать: АМ = ВМ
Доказательство:
Если точка М совпадает с точкой О, то равенство АМ = ВМ верно.
Пусть М и О – различные точки.
Прямоугольные треугольники ОАМ и ОВМ равны по двум катетам (ОА = ОВ по условию, ОМ – общий катет), из равенства треугольников следует, что АМ = ВМ.
Докажем обратное утверждение.
Дано:
АВ – отрезок, N – произвольная точка такая, что АN = ВN.
Доказать:
точка N лежит на прямой m – серединном перпендикуляре к АВ.
Доказательство:
если точка N – точка прямой АВ, то она совпадает с серединой О отрезка АВ и потому лежит на прямой m.
Если же точка N не лежит на прямой АВ, то треугольник АNВ – равнобедренный, так как АN = ВN.
Отрезок NО является медианой равнобедренного треугольника, значит, она является и его высотой.
Таким образом, NО перпендикулярен АВ, поэтому прямые ОN и m совпадают, т.е. точка N – точка прямой m.
Теорема доказана.
Следствием доказанной теоремы является следующее утверждение.
Следствие: серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
§ 3 Теорема о пересечении высот теугольника
Рассмотрим еще одну теорему о пересечении высот треугольника.
Теорема:
Высоты треугольника (или их продолжения) пересекаются в одной точке.
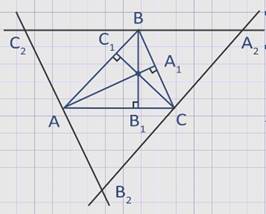
Дано:
АА1 , ВВ1, СС1 – высоты треугольника АВС.
Доказать:
АА1 , ВВ1, СС1 пересекаются в точке О.
Доказательство:
Проведем через вершины А, В и С прямые, параллельные противоположным сторонам треугольника.
Получим треугольник А2В2С2.
Точки А, В, С являются серединами треугольника А2В2С2.
Действительно, в параллелограммах АВА2Си АВСВ2 противоположные стороны равны, т.е. АВ = А2С, АВ = СВ2 , поэтому А2С = СВ2.
Аналогично С2А = АВ2 и С2В = ВА2.
Из построения следует, что СС2 перпендикулярно А2В2, АА1 перпендикулярно В2С2, ВВ1 перпендикулярно А2С2.
Таким образом, прямые АА1, ВВ1, СС1 являются серединными перпендикулярами к сторонам треугольника А2В2С2, следовательно, они пересекаются в одной точке.
Теорема доказана.
Решим задачу, используя полученные знания.
Задача.
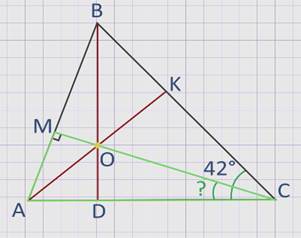
В треугольнике АВС проведены высоты АК и ВD, пересекающиеся в точке О.
Угол САВ = 42°.
Найдите величину угла АСО.
Дано:
∆АВС, АК и ВD – высоты треугольника АВС, пересекающиеся в точке О, ∠САВ = 42°
Найти:
∠АСО.
Решение:
для вычисления угла АСО проведем еще одну высоту СМ треугольника АВС, по теореме о пересечении высот треугольника высота СМ пройдет через точку О, а значит, треугольник АСМ – прямоугольный.
Тогда ∠АСО = 180° – (90° + 42°) = 48°.
В этом уроке познакомились с замечательными точками треугольника, рассмотрели теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку и их следствия, теорему о пересечении высот (или их продолжений), а также рассмотрели решение задачи по теме урока.
Список использованной литературы:
- Л.С. Атанасян. Учебник. 8 класс.
- Н.Ф. Гаврилова. Поурочные разработки по геометрии. 8 класс. – Москва: «Вако», 2005.
- Л.С. Атанасян и др. Методические рекомендации к учебнику. – Москва: «Просвещение», 2001.
- Д.А. Мальцева. Математика. 9 класс. ГИА 2014. – Москва: Народное образование, 2013.
- О.В. Белицкая. Геометрия. 8 класс. Тесты. – Саратов: «Лицей», 2009.
- С.П. Бабенко, И.С. Маркова. Геометрия 8. Комплексная тетрадь для контроля знаний. – Москва: «Аркти», 2014.
Медиана биссектриса и высота треугольника видеоурок
7 класс, 17 урок, Медианы, биссектрисы и высоты треугольника
ГЕОМЕТРИЯ 7 класс : Медиана, биссектриса, высота треугольника | Видеоурок
Геометрия 7 класс (Урок№12 – Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)
Определение:
Медианой
треугольника называется отрезок, соединяющий вершину треугольника с серединой
противолежащей стороны.
Например,
возьмём треугольник АВС.
Если
точки А1, В1 и С1 –
соответственно середины сторон ВС, СА и АВ, то отрезки АА1, ВВ1
и СС1 – медианы этого треугольника. Медианы, проведённые из вершин А, В и С (или их длины) треугольника АВС можно обозначить:
Определение:
Биссектрисой
треугольника называется отрезок биссектрисы угла треугольника, соединяющий
вершину треугольника с точкой противолежащей стороны.
Например,
возьмём некоторый треугольник АВС.
Проведём
биссектрису АЕ1 угла ВАС, ВЕ2 –
угла АВС и СЕ3 – угла АСВ. Биссектрисы, проведённые из вершин А, В и С (или их длины) треугольника АВС можно обозначить:
Определение:
Высотой
треугольника называется перпендикуляр, проведённый из его вершины к прямой, содержащей противоположную сторону.
Изобразим
треугольник АВС и отрезки АF1,
BF2
и CF3,
которые являются высотами нашего треугольника.
Высоты,
проведённые из вершин А, В и С (или их длины)
треугольника АВС можно обозначить:
Свойства:
1.
Медианы треугольника пересекаются в одной точке.
2.
Биссектрисы треугольника пересекаются в одной точке.
3.
Высоты или прямые, содержащие высоты, пересекаются в одной точке.
Ответим
на вопрос: Может ли точка пересечения высот лежать вне треугольника?
Да,
когда у него один угол тупой.
А
может ли точка пересечения высот лежать в вершине треугольника?
Да,
может, когда у треугольника есть прямой угол.
Пример.
Рассмотрим
следующую задачу. Отрезок BD
–
медиана треугольника АВС, отрезок ВЕ – медиана треугольника DBC. Чему равна длина отрезка АС, если
отрезок ЕС=4 см.?
Так
как ВЕ – медиана треугольника DBC,
то отрезок DE=ЕС.
Следовательно, сторона DC=2*ЕС,
то есть DC=8
см.
BD
–
медиана треугольника АВС, значит, отрезок AD=DC. Следовательно, сторона АС=2*DC. Так как отрезок DC=8 см., то длина стороны АС=16 см.
Ответ:
16 см.
Пример.
Отрезок
AD
–
медиана треугольника АВС. Точка Е лежит на луче АD так, что AD равняется DЕ. Докажите, что треугольник АDВ
равен треугольнику CDE.
Так
как AD
–
медиана треугольника АВС, то СD равняется DB.
Рассмотрим
треугольники АDВ
и CDE.
У них сторона AD
равна стороне DЕ
по условию задачи; сторона СD
равна стороне DB,
так как AD
–
медиана; а углы ADB
и
CDE
равны как вертикальные.
Следовательно,
треугольник АDВ
равен треугольнику CDE
по первому признаку равенства треугольников.
0
0
05:32
Медиана, биссектриса, высота
Медиана треугольника — отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В любом треугольнике можно провести 3 медианы. Все они пересекаются в одной точке, в центре (центре тяжести) треугольника.
Биссектриса треугольника — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой на противолежащей стороне.
Высота треугольника — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Следующие уроки
05:05
02:27
02:03
06:11
03:36