Как найти биссектрису тупого угла

Треугольник. Медиана, биссектриса, высота, средняя линия.

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Остроугольные	Тупоугольные	Прямоугольные
Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС.	Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой.	Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

• CD – внутренняя биссектриса ∠ACB;
• CE – биссектриса угла, смежного с ∠ACB;
• ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Все формулы биссектрисы в треугольнике

L – биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b – стороны треугольника

с – сторона на которую опущена биссектриса

d, e – отрезки полученные делением биссектрисы

γ – угол ABC , разделенный биссектрисой пополам

p – полупериметр, p =(a+b+ c )/2

Длина биссектрисы через две стороны и угол, ( L ):

Длина биссектрисы через полупериметр и стороны, ( L ):

Длина биссектрисы через три стороны, ( L ):

Длина биссектрисы через стороны и отрезки d , e , ( L ):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

[spoiler title=”источники:”]

http://www-formula.ru/bisectortriangle

[/spoiler]

Биссектриса угла

2 июня 2018

• Домашняя работа
• Ответы и решения

Сегодня будет очень лёгкий урок. Мы рассмотрим всего один объект — биссектрису угла — и докажем важнейшее её свойство, которое очень пригодится нам в будущем.

Только не надо расслабляться: иногда ученики, желающие получить высокий балл на том же ОГЭ или ЕГЭ, на первом занятии даже не могут точно сформулировать определение биссектрисы.

И вместо того, чтобы заниматься действительно интересными задачами, мы тратим время на такие простые вещи. Поэтому читайте, смотрите — и берите на вооружение.:)

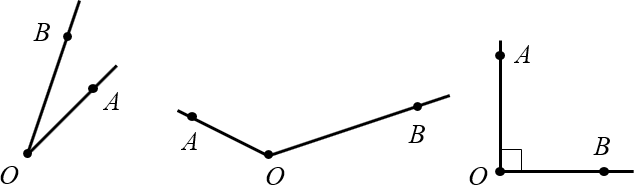
Для начала немного странный вопрос: что такое угол? Правильно: угол — это просто два луча, выходящих из одной точки. Например:

Как видно из картинки, углы могут быть острыми, тупыми, прямыми — это сейчас неважно. Часто для удобства на каждом луче отмечают дополнительную точку и говорят, мол, перед нами угол $AOB$ (записывается как $angle AOB$).

Капитан очевидность как бы намекает, что помимо лучей $OA$ и $OB$ из точки $O$ всегда можно провести ещё кучу лучей. Но среди них будет один особенный — его-то и называют биссектрисой.

Определение. Биссектриса угла — это луч, который выходит из вершины этого угла и делит угол пополам.

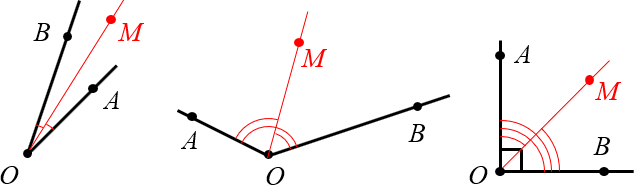
Для приведённых выше углов биссектрисы будут выглядеть так:

Поскольку на реальных чертежах далеко не всегда очевидно, что некий луч (в нашем случае это луч $OM$) разбивает исходный угол на два равных, в геометрии принято помечать равные углы одинаковым количеством дуг (у нас на чертеже это 1 дуга для острого угла, две — для тупого, три — для прямого).

Хорошо, с определением разобрались. Теперь нужно понять, какие свойства есть у биссектрисы.

Основное свойство биссектрисы угла

На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:

Теорема. Биссектриса угла — это геометрическое место точек, равноудалённых от сторон данного угла.

В переводе с математического на русский это означает сразу два факта:

1. Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
2. И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.

Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:

Определение. Расстояние от точки до прямой — это длина перпендикуляра, проведённого из данной точки к этой прямой.

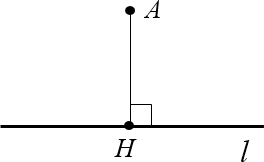
Например, рассмотрим прямую $l$ и точку $A$, не лежащую на этой прямой. Проведём перпендикуляр $AH$, где $Hin l$. Тогда длина этого перпендикуляра и будет расстоянием от точки $A$ до прямой $l$.

Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:

Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.

Как и обещал, разобьём доказательство на две части:

1. Расстояния от точки на биссектрисе до сторон угла одинаковы

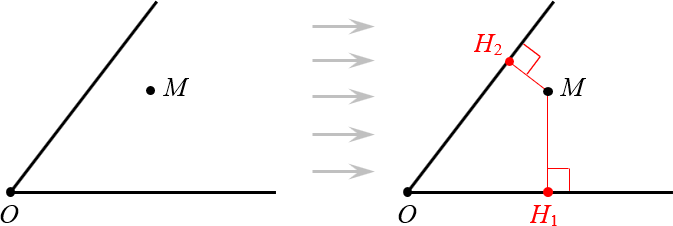
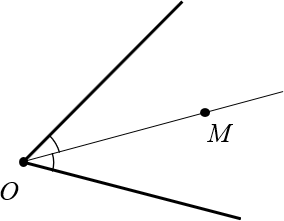
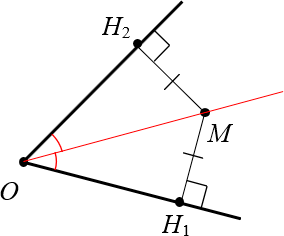
Рассмотрим произвольный угол с вершиной $O$ и биссектрисой $OM$:

Докажем, что эта самая точка $M$ находится на одинаковом расстоянии от сторон угла.

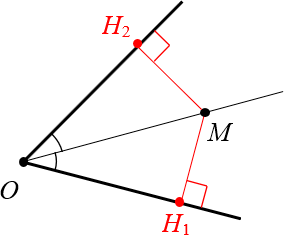
Доказательство. Проведём из точки $M$ перпендикуляры к сторонам угла. Назовём их $M{{H}_{1}}$ и $M{{H}_{2}}$:

Получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. У них общая гипотенуза $OM$ и равные углы:

1. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$ по условию (поскольку $OM$ — биссектриса);
2. $angle M{{H}_{1}}O=angle M{{H}_{2}}O=90{}^circ $ по построению;
3. $angle OM{{H}_{1}}=angle OM{{H}_{2}}=90{}^circ -angle MO{{H}_{1}}$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.

Следовательно, треугольники равны по стороне и двум прилежащим углам (см. признаки равенства треугольников). Поэтому, в частности, $M{{H}_{2}}=M{{H}_{1}}$, т.е. расстояния от точки $O$ до сторон угла действительно равны. Что и требовалось доказать.:)

2. Если расстояния равны, то точка лежит на биссектрисе

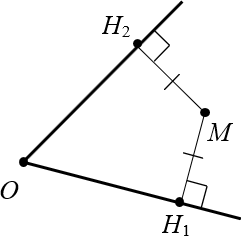
Теперь обратная ситуация. Пусть дан угол $O$ и точка $M$, равноудалённая от сторон этого угла:

Докажем, что луч $OM$ — биссектриса, т.е. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$.

Доказательство. Для начала проведём этот самый луч $OM$, иначе доказывать будет нечего:

Снова получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. Очевидно, что они равны, поскольку:

1. Гипотенуза $OM$ — общая;
2. Катеты $M{{H}_{1}}=M{{H}_{2}}$ по условию (ведь точка $M$ равноудалена от сторон угла);
3. Оставшиеся катеты тоже равны, т.к. по теореме Пифагора $OH_{1}^{2}=OH_{2}^{2}=O{{M}^{2}}-MH_{1}^{2}$.

Следовательно, треугольники $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$ по трём сторонам. В частности, равны их углы: $angle MO{{H}_{1}}=angle MO{{H}_{2}}$. А это как раз и означает, что $OM$ — биссектриса.

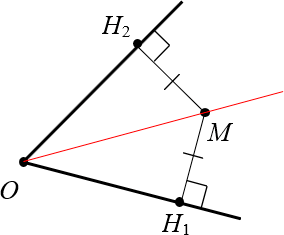
В заключение доказательства отметим красными дугами образовавшиеся равные углы:

Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)

Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.

Смотрите также:

1. Перпендикулярные прямые — определение и свойства
2. Что такое вертикальные углы
3. Следствия из теоремы Виета
4. Работа с формулами в задаче B12
5. Пример решения задачи 15
6. Задача B15: частный случай при работе с квадратичной функцией

Как найти биссектрису угла

Биссектрисой называется такой луч, который, будучи проведенным из вершины угла, делит его пополам. Будучи проведенной из вершины угла, биссектриса становится отрезком, который делит образованный двумя сторонами угол на 2 равные части. Длину этого отрезка можно вычислить разными путями.

Вам понадобится

• Данные о сторонах и углах треугольника.

Инструкция

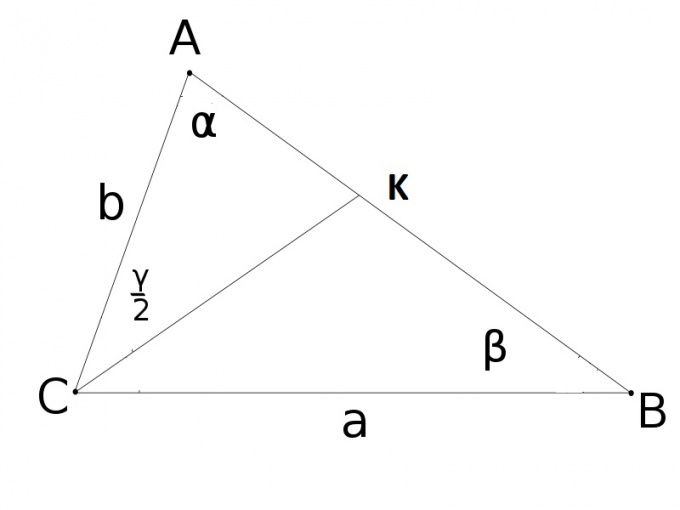
Имеется треугольник ABC, который обладает сторонами a,b,c. Помимо этого, у него есть CK – биссектриса, проведенная из точки С к стороне AB, p – это 1/2 периметра треугольника ABC, AK и KC – отрезки, получившиеся из-за деления биссектрисой стороны AB, ?, ? и ? – углы, принадлежащие вершинам A, B, С соответственно, h – высота, которая проведена из точки C к противолежащей стороне AB. Зная эти данные, вычислить длину биссектрисы можно, используя следующие равенства:
1) CK = v(a*b(a+b+c)*(a+b-c))/a+b=v(4*a*b*p(p-c))/a+b;
2) CK = v(a*b – AK*KC);
3) CK = (2*a*b*cos(?/2))/a+b;
4) CK = h/cos(?-?/2).

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

2.1. Даны уравнения
двух прямых. Составить
уравнение биссектрисы тупого угла,
образованного этими прямыми.

Общие
сведения и расчётные формулы:по представленному заданию.

Пусть
имеем две прямые:
:

x+y+=0
и
:

x+y+=0.
Уравнением

определя­ется вектор нормали
,
уравнением

вектор нормали
.
Так как векторы

и
–
свободные, то изобразим их так, чтобы
их начала принадлежали соответствующим
плоскостям, а сами они располагались
внутри одного из углов, образованных
пересекающимися прямыми. Важно помнить
также, что уравнение прямой можно
умножать на произвольное, не равное
нулю число. Это значит, что, по необходимости,
мы можем разместить векторы

и

как внутри тупого, так и внутри острого
угла. Пусть векторы

и

разместились внутри тупого угла, как
показано на рисунке. Умножим уравнение

на число (-1). Вектор нормали этой прямой
станет равным
,
и пара векторов

и

располо­жится внутри острого угла.
Видим,
когда векторы нормалей плоскостей
располагаются внутри тупого угла угол
между ними острый. И наоборот, если
векторы расположились внутри острого
угла, то угол между ними тупой. Какой из
случаев реализуется в конкретном
примере, легко определить при помощи
скалярного произведения:

а)

∙
> 0 – век­торы расположены в области
тупого угла;

б)

∙
< 0 – векторы расположены в области
ост­рого угла.

Так как от случая
а) легко перейти к случаю б), то для
определённости будем считать, что всегда
нужно строить биссектрису тупого угла.

Отметим
факт: рассматриваемую задачу относят
кклассическим
задачам аналитической геометрии. Важно
также то, что существует несколько
способов решения этой задачи, причём
существенно различающихся как по
теоретическим основам, так и технологии
применяемых вычислений!

Способ–1.
Пусть
∙
> 0: векторы

и

располагаются в области тупого угла.

Воспользуемся
свойством биссектрисы: каждая принадлежащая
ей точка одинаково уда­лена от сторон
угла, который биссектриса делит пополам.

Для
эффективного (и удобного) исполь­зования
понятия расстояние
от точки до пря­мой,
каждое из уравнений заданных прямых
необходимо нормализовать. Нормированное
урав­нение прямой удобно как для
вычисления отклонения точки от плоскости,
так и для вычисления рас­стояния от
точки до плоскости. В нашем случае задача
упрощается, так как отклонения

и

произвольной точки биссектрисы от
прямых

и

имеют одинаковые знаки и можно записать:

=.
Это значит уравнение биссектрисы, как
геометрическое место точек, равноудалённых
от сторон угла, которому эта биссектриса
принадлежит, можно записать в виде:

=. (B¹)

Если бы теперь
нужно было построить биссектрису острого
угла, то её уравнение должно быть записано
в виде:

=
–. (B²)

Замечание:
Если
бы векторы

и

располагались в области острого угла,
то биссектриса острого угла определялась
бы выражением (B¹),
а биссектриса тупого – выражением
(B²).

Способ–2.
В этом случае примем схему решения
задачи: а) находим точку M₀(x₀,y₀)
пересече­ния прямых

и
;
б) находим направление биссектрис
;
в) проводим прямую через заданную точку
в заданном направлении.

Для
определения направления биссектрис
l_В
построим единичные векторы:

и
,
затем суммы:
=+
– этот вектор определяет направление
биссектрисы угла, содержащего векторы

,;

=––
определяет направле­ние биссектрисы
угла, смежного первому.

Используя
угловой коэффициент вектора
,
строим биссектрису угла, содержащего
век­торы
,;
если использовать угловой коэффициент
век­тора
,
построим биссектрису смеж­ного угла.

Замечание: на
самом деле, достаточно найти только
один вектор:
для первой биссектрисы он играет роль
направляющего вектора, а для второй –
роль вектора нормали.

Способ–3.
Воспользуемся уравнением пучка прямых:

:

и вектором
.
Параметр

прямой

выбирается из условия:
.

Интересно рассмотреть
один и тот же пример, решив его сразу
всеми тремя способами: это позволит
сравнить их трудоёмкости!

Пример
(и образец оформления):

Общая часть.
Составить уравнение
биссектрисы тупого угла, образованного
пересекающимися прямыми:и.

Задачу
решим, применяя все рассмотренные
способы.

Способ–1.
Используем равенство отклонений=каждой точки биссектрисы от сторон
тупого угла, которому она принадлежит.

Решение:

1). Запишем векторы:
,.
Вычислим:∙=3·12+(-4)·5>0.
Это значит, что векторыирасполагаются в области тупого угла.

2). Общая запись
уравнения биссектрисы имеет вид:
=,
а в нашем случае:=,
откуда получаем уравнение искомой
биссектрисы:.

Ответ:.

Способ–2.
В этом случае применим схему решения
задачи: а) находим точкупересечения прямыхи;
б) находим направление бис­сектрис;
в) проводим прямую через заданную точку
в заданном направлении.

Решение:

1). Координаты
находим из системы урав­нений:
→=.

2). Так как
и,
тои.
Тогда:=–=–(3,11).
Векторможно принять в качестве нормали искомой
биссектрисы. Удобнее принять коллинеарный
ему вектор:.

3). Общее уравнение
биссек­трисы запишем в виде:
.
В нашем примере: 3+11=0,
или.

Ответ:.

Способ–3.
Воспользуемся уравнением пучка прямых:,
или в виде:и направляющим вектором=(11,–3)..

Решение:

1). Вычислим угловой
коэффициент прямой пучка:
.

2). Вычислим угловой
коэффициент направляющего вектора: –.

3). Воспользуемся
равенством:
=–,
откуда получаем:.

4). Подставляем
значение
в уравнение:.
Окончательно записываем уравнение
искомой биссектрисы:.

Ответ:.

Выводы: 1).
В рассматриваемой задачеСпособ–1демонстрирует великолепные возмож­ности
использования нормальных уравнений
прямой!

2). Применение
Способа–3демонстрирует эффективность использования
конструкциипучок.

3). Применение
Способа–2также полезно, так как требует минимум
специальных знаний. Это может сработать
при выполнении контрольной работы!

Замечание:
при оформлении задания использование
рисунка (в карандаше, с использованием
чертёжных инструментов)обязательно!

Варианты
индивидуальных заданий:

Вар.	Задание:	Вар.	Задание:
1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

2.2. Даны координаты
вершин
итреугольникаи точкапересечения его высот. Найти координаты
вершинытреугольника.

Общие
сведения и расчётные формулы:по представленному заданию.

Пусть
прямая
:

x+y+=0
определяет сторону

треугольника, а прямая
:x+y+=0
сторону
.
Тогда вектор

можем принять в качестве нормали прямой

,
а вектор

в качестве нормали прямой
.
Остаётся воспользоваться уравнением
прямой, для которой задан вектор нормали
и точка, принадлежащая прямой! Как только
будут построены уравнения прямых,
нетрудно найти их точку пересечения .

Пример
(и образец оформления):

Общая часть.
Пусть вершиныитреугольника:=(-10,2),=(6,4)
и точка пересечения его высот:=(5,2).
Найти координаты вершины.

Решение:

1)
Вычислим: =–=(5,2)–(6,4)=(-1,-2)=;=–=(5,2)–(-10,2)=(15,0)=.

2). Заменим полученные
векторы нормалей коллинеарныvми
им, но более простые в записи:

=(1.2),

=(1,0).

3). Воспользуемся
общим уравнение прямой для случая, когда
задан вектор нормали прямой и точка,
принадлежащая прямой:
.
Тогда получим:

:
→;

:
→.

4). Вычислим
координаты точки
:откуда,.

Ответ:=.

Замечание:
при оформлении задания использование
рисунка (в карандаше, с использованием
чертёжных инструментов)обязательно!

Варианты
индивидуальных заданий:

Вар.	Задание:	Вар.	Задание:
1.				16.
2.				17.
3.				18.
4.				19.
5.				20.
6.				21.
7.				22.
8.				23.
9.				24.
10.				25.
11.				26.
12.				27.
13.				28.
14.				29.
15.				30.

2.3. Даны координаты
вершин треугольника
.
Составить уравнения:
стороны ,высоты, биссектрисы
и медианы, проведённых из вершины A.

Общие
сведения и расчётные формулы:по представленному заданию.

Для решения задачи
необходимо вспомнить формулы, определяющие
уравнение прямой, для случаев:

1^*.
Заданы две точки, принадлежащие прямой.
Тогда уравнение прямой, проходящей
через две заданные точки записывают в
форме
:

,
где
=.

2^*.
Заданы: точка A,
принадлежащая прямой, и направление
прямой. Для построения уравнения прямой,
содержащей высоту, опущенную на
,
учтём:
.
Это значит:
.
Так как

после построения уравнения

будет известно, то уравнение прямой

может быть записано в виде :
,
где
=.

3^*.
Тремя точками
задан угол с вершиной в точке .
Прямая

проходит через точку
и делит угол:
пополам. Эту задачу можно решить двумя
вариантами:

а).
Используем равенство углов: =.
Обозначив угловой коэффициент прямой

через
,
запишем:
=,
причём угловые коэффициенты сторон
заданного угла вычисляют по формулам:

,

.
Для искомой прямой уравнение принимает
вид:
:

.

б).
Определим направление стороны
угла

единичным вектором:
,
стороны –
единичным
вектором:
.
Тогда направляющий вектор прямой,
совпадающей с биссектрисой может быть
записан в виде:
.
После этого остаётся воспользоваться
каноническим уравнением прямой:
=.

4^*.
Заданы : точка
,
принадлежащая прямой, и концы отрезка

точками

и
.
Прямая

совпадает с медианой, проведённой из
точки

к середине отрезка
–
точке
.
Далее задача совпадает с задачей 1^*:
записываем уравнение прямой, проходящей
через две заданные точки записывают в
форме
:

,
где
=.

Пример
(и образец оформления):

Общая часть.
Пусть задан треугольникего вершинами:,,.
Составить уравнения:
стороны ,высоты, медианы и
биссектрисы, проведённые из вершины A.

Решение
задачи 1^*.

1). Уравнение прямой
,
содержащей точкии:,
где=.

2). Вычислим
===4.

3). Запишем уравнение
прямой
:,
или в виде:.

Ответ:.

Решение
задачи 2^*.

1). Уравнение прямой
,
содержащей высоту,
опущенную на :,
где=.

2). Учитывая результат
задачи 1*, вычислим
==.

3). Запишем уравнение
прямой
:,
или в виде:.

Ответ:.

Решение
задачи 3^*.

1). Уравнение
биссектрисы
определим двумя способами.

Способ-1.
Общая запись уравнения::y–=(x–),
гдевычисляем
из выражения:=,
причём,.

1). Вычислим
,.
Тогда=0.

2). Уравнение
принимает вид:.

Ответ:.

Способ-2.
Общая запись канонического уравнения:=,
где=,
причём,==;===.

1). Вычислим:
==(4,-3)
–(1,1)=(3,-4);=5
→=(3,–4);

==(7,
9) –(1, 1)=(6,8);=10
→=(3,4).

2). Тогда:
=(3,–4)+(3,4)=(3,0)
→ принимаем:=(1,0).

3). Получили уравнение
в виде:=,
или:.

Ответ:.

Решение
задачи 4^*.

1). Уравнение прямой
,
содержащей медиану,
проведённую из точкик середине отрезка–
точке,
имеет вид:,
где=.

2). Вычислим
координаты точки M
из условия: =,
илиM===.

3). Тогда:
==и уравнениепринимает вид:,
или:.

Ответ:.

Замечание:
при оформлении задания использование
рисунка (в карандаше, с использованием
чертёжных инструментов)обязательно!

Варианты
индивидуальных заданий:

Вар.	Задание:	Вар.	Задание:
1.				16.
2.				17.
3.				18.
4.				19.
5.				20.
6.				21.
7.				22.
8.				23.
9.				24.
10.				25.
11.				26.
12.				27.
13.				28.
14.				29.
15.				30.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #