Элементы треугольника. Биссектриса
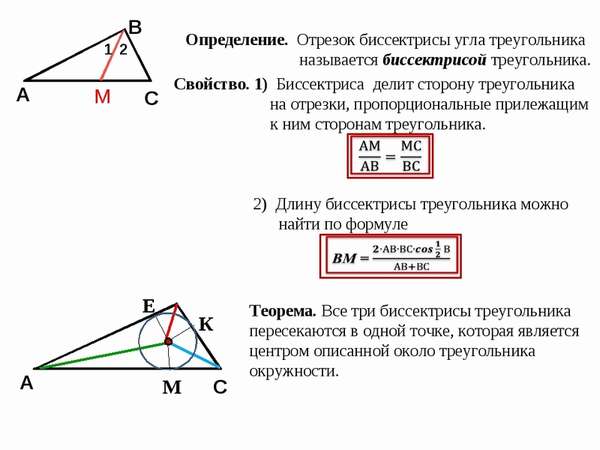
Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.
Свойства биссектрисы
1. Биссектриса треугольника делит угол пополам.
2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()
3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.
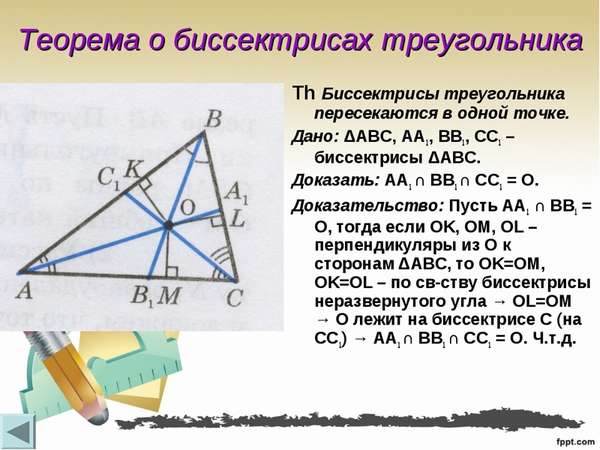
4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.
Некоторые формулы, связанные с биссектрисой треугольника
(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,
Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.
Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1
Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Медианы, биссектрисы и высоты треугольника
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы продолжим рассмотрение элементов треугольника – медиан, биссектрис и высот треугольника.
Вначале дадим определение медианы треугольника и рассмотрим три медианы треугольника. Дадим определение биссектрисы треугольника и рассмотрим три биссектрисы треугольника. Дадим определение высоты треугольника и рассмотрим высоты в произвольном треугольнике и в тупом треугольнике. Далее решим ряд задач с использованием этих элементов.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
[spoiler title=”источники:”]
http://interneturok.ru/lesson/geometry/7-klass/treugolnikib/mediany-bissektrisy-i-vysoty-treugolnika
[/spoiler]
Канал видеоролика: Геометрия 7-11 класс

Смотреть видео:
#математикаогэ #гвэ #егэответы #числа #математика #алгебра #подготовкакогэ #ответы_огэ #подготовкакегэ
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

Как с помощью одной линейки построить касательную к окружности?
GetAClass – Просто математика
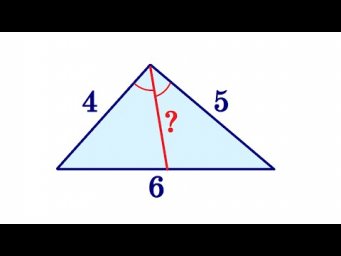
Найдите биссектрису большего угла треугольника со сторонами 4, 5 и 6 ★ 2 способа решения
Valery Volkov

Найдите биссектрису угла треугольника на рисунке ★ Два способа
Valery Volkov

Быстро и точно строим биссектрису любого угла
Геометрия 7-11 класс
Облегчи жизнь другим ученикам – поделись! (плюс тебе в карму):
29.04.2021
 Математика, как известно, царица наук. Неслучайно это выражение так любят учителя, особенно старой формации. Математика открывается исключительно тем, кто умеет, во-первых, логически мыслить, а во-вторых, тем, кто любит всегда добиваться ответа, оперируя изначальными условиями, не жульничая, а основывая решения на анализе, построение опять-таки логических связей. Эти качества, вынесенные со школьной скамьи, способны модулироваться и к взрослой серьезной жизни как в рабочих, так и в иных сложных моментах.
Математика, как известно, царица наук. Неслучайно это выражение так любят учителя, особенно старой формации. Математика открывается исключительно тем, кто умеет, во-первых, логически мыслить, а во-вторых, тем, кто любит всегда добиваться ответа, оперируя изначальными условиями, не жульничая, а основывая решения на анализе, построение опять-таки логических связей. Эти качества, вынесенные со школьной скамьи, способны модулироваться и к взрослой серьезной жизни как в рабочих, так и в иных сложных моментах.
Оглавление:
- Свойства
- Свойства в равнобедренных треугольниках
- Определение биссектрисы треугольника
- Определение длины
- Нахождение величины угла
Сегодня многие сталкиваются с проблемами при решении математических задач еще в начальной школе.
Однако даже те школьники, которые успешно осваивают первичную математическую программу, переходя на новый школьный и жизненный этап, где алгебра отделяется от геометрии, бывает, сталкиваются с серьезными затруднениями. Между тем, один раз выучив и, главное, поняв, как найти биссектрису треугольника, ученик навсегда запомнит эту формулу. Рассмотрим треугольник ABC с тремя проведенными биссектрисами. Как видно из рисунка, все они сходятся в одной точке.
Во-первых, определим, что биссектриса треугольника, и это одно из важнейших ее свойств, делит угол, из которого такой отрезок исходит, пополам. То есть в приведенном примере угол BAD равен углу DAC.
Это интересно: Как найти периметр треугольника.
Свойства
- Биссектриса треугольника разделяет сторону, к которой она проведена на два отрезка, обладающие свойствами пропорциональности к сторонам, которые прилегают к каждому отрезку, соответственно. Таким образом, BD/CD = AB/AC.
- Каждый треугольник способен обладать тремя данными отрезками. Другие значимые свойства касаются как частных, так и общих случаев конкретных рассматриваемых треугольников.
Свойства в равнобедренных треугольниках
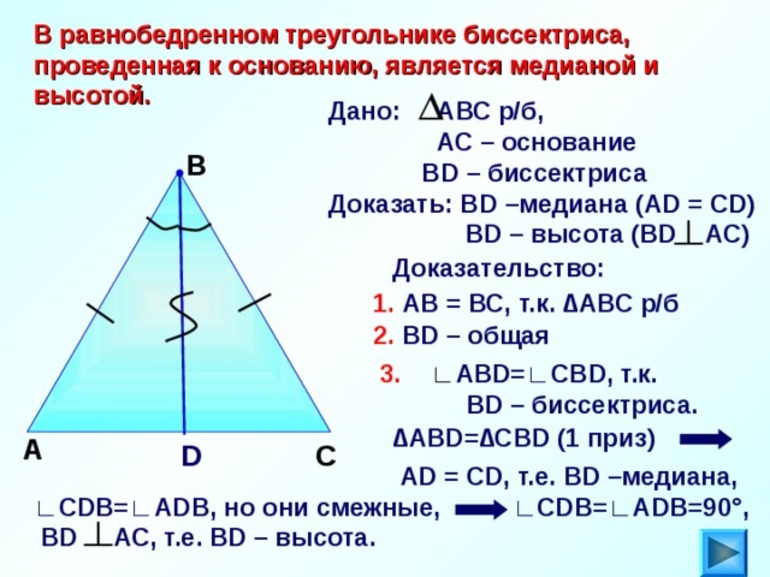
 Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.- Разумеется, что будет верным и обратное свойство. То есть в равнобедренном треугольнике неизменно наблюдается равенство двух его биссектрис.
- Из сказанного ранее вытекает вывод о том, что биссектриса, исходящая из противоположного основанию, служит также медианой и высотой.
- Все биссектрисы равностороннего треугольника обладают равенством.
Определение биссектрисы треугольника
Допустим, что в рассматриваемом треугольнике ABC сторона AB = 5 cm, AC = 4 cm. Отрезок CD = 3 cm.
Определение длины
Определить длину можно по следующей формуле. AD = квадратный корень из разности произведения сторон и произведения пропорциональный отрезков.
 Найдем длину стороны BC.
Найдем длину стороны BC.
- Из свойств известно, что BD/CD = AB/AC.
- Значит, BD/CD = 5/4 = 1,25.
- BD/3 = 5/4.
- Значит, BD = 3,75.
- ABxAC = 54=20.
- CDxBD = 33,75 = 11,25.
Так, для того чтобы рассчитать длину, требуется вычесть из 20 11,25 и извлечь квадратный корень из получившегося 8,75. Результат с учетом тысячных долей получится 2,958.
Данный пример призван также эксплицитно указать на ситуацию, когда значения длины биссектрисы, как и все другие значения в математике, будут выражены не в натуральных числах, однако бояться этого не стоит.
Это интересно: в чем выражается эволюционный характер развития общества?
Нахождение величины угла
Для нахождения углов, образующихся биссектрисой, важно, прежде всего, помнить о сумме углов, неизменно составляющей 180 градусов. Предположим, что угол ABC равен 70 градусам, а угол BCA 50 градусам. Значит, путем простейших вычислений получим, что CAB = 180 (70+50) = 60 градусов.
Если использовать главное свойство, в соответствии с которым угол, из которого она исходит, делится пополам, получим равные значения углов BAD и CAD, каждый из которых будет 60/2 = 30 градусов.
Если требуется дополнительный наглядный пример, рассмотрим ситуацию, когда известен лишь угол BAD равный 28 градусам, а также угол ABC равный 70 градусам. Используя свойство биссектрисы, сразу найдем угол CAB путем умножения значения угла BAD на два. CAB = 282 =56. Значит, BAC = 180 (70+56) или 180 (70+282)= 180 126 = 54 градуса.
Специально не рассматривалась ситуация, когда данный отрезок выступает в качестве медианы или высоты, оставив для этого другие специализированные статьи.
Таким образом, мы рассмотрели такое понятие, как биссектриса треугольника, формула для нахождения длины и углов которой заложена и реализована в приведенных примерах, имеющих целью наглядно показать, каким образом можно использовать для решения тех или иных задач в геометрии. Также к данной теме относятся такие понятия, как медиана и высота. Проведите ночь в компании красивой проститутки СПБ . Посетите наш онлайн-портал, и вы обнаружите подборку самых способных девушек своего города. Изучите все доступные варианты, и мы посодействуем вам в выборе подходящей спутницы! Если данный вопрос прояснился, следует обращаться к дальнейшему изучению различных других свойств треугольника, без которых немыслимо дальнейшее изучение геометрии.
Биссектриса треугольника 


Процесс построения
Биссектриса (лат. bisectio) представляет собой геометрическое место точек внутри угла (острый, прямой или тупой), которые одинаково удалены от обеих его сторон.
Для её построения нужно подготовить различные школьные принадлежности и выполнить несколько простых действий.
Подготовительный этап
Чтобы быстро найти биссектрису треугольника с помощью циркуля, нужно провести тщательную подготовку. Она заключается в поиске школьных принадлежностей, которые будут использоваться при построении.
Необходимые предметы:

- простой карандаш;
- линейка;
- ластик;
- циркуль;
- лист бумаги.
Порядок действий
Нарисовать луч, разделяющий пополам угол, можно при помощи транспортира. Однако если этой школьной принадлежности нет в наличии, заменить её сможет обыкновенный циркуль.
Быстрый способ:
- На листе бумаги рисуют 2 пересекающиеся линии.
- Чтобы построить биссектрису данного угла, в его вершину ставят ножку циркуля и чертят окружность произвольного радиуса.
- Отмечают точками места пересечения сторон угла с окружностью.
- На них поочерёдно ставят циркуль и, не меняя радиус, рисуют 2 дуги.
- Находят и отмечают место их пересечения.
- Стирают дуги ластиком, чтобы они не мешали дальнейшей работе.
- С помощью линейки и простого карандаша проводят искомый отрезок, соединяющий вершину угла с точкой пересечения дуг.
С помощью циркуля можно легко найти биссектрису треугольника (всякого). Для этого понадобится стандартный набор школьных принадлежностей и наличие базовых знаний геометрии.
Порядок действий:
- Любым известным способом вписывают окружность в треугольник.
- С помощью карандаша и линейки из её центра проводят линии к каждой вершине.
- Полученные отрезки станут частью искомого луча.
Альтернативный вариант
Если у ученика нет циркуля, то начертить луч, разделяющий угол пополам, можно и без этой школьной принадлежности. Для работы понадобится линейка, карандаш и транспортир.
Правильная последовательность действий:
- Нулевое значение на шкале прикладывают к вершине.
- Совмещают линейку транспортира с одним из лучей и определяют величину угла.
- Полученное значение делят пополам.
- Затем заново прикладывают транспортир и откладывают величину, полученную в результате расчётов.
- Через эту точку и вершину проводят отрезок, который будет являться искомым лучом.
Полезные советы
В некоторых случаях для нахождения не нужно использовать транспортир и циркуль. Это возможно только тогда, когда нужно определить расположение биссектрисы в треугольнике.
Полезные рекомендации:
- Биссектриса всегда разделяет противолежащую сторону треугольника в отношении, равном пропорции 2 других сторон геометрической фигуры.
- В равнобедренном треугольнике биссектрисы всегда пересекаются под прямым углом.
- Если треугольник равносторонний, то все биссектрисы будут параллельны противоположным сторонам. При этом длина образованных отрезков будет одинаковой.
Построить биссектрису угла с помощью циркуля сможет даже двоечник. Для этого ему понадобится минимум времени, знаний и усилий. Подробно изучив порядок действий, каждый учащийся сможет легко поделить любой угол пополам и объяснить этот процесс одноклассникам.
Треугольник в геометрии — основная фигура, которую нельзя разделить на составляющие. Отрезок прямой линии, соединяющий вершину с противоположной стороной, при условии разделения угла пополам, — это биссектриса треугольника. Так как данная фигура содержит 3 угла, соответственно, из каждого можно провести линию, делящую его на равные компоненты.
Оглавление
- Свойства биссектрисы
- Характеристика внутренних линий
- Пример
- Соотношение со сторонами треугольника
- Пример
- Способы построения
- Полезное видео
- Подведем итоги
Свойства биссектрисы
 Равносторонняя треугольная фигура характеризуется не только равенством сторон, но внутренние углы также одинаковы, при этом они составляют 60° каждый.
Равносторонняя треугольная фигура характеризуется не только равенством сторон, но внутренние углы также одинаковы, при этом они составляют 60° каждый.
Поэтому проведенная биссектриса одновременно является высотой, медианой. Она обладает не только своими качествами, но и характеристиками высоты, медианы треугольника:
- делит противоположные стороны на равные части;
- перпендикулярна к противолежащей стороне;
- в точке пересечения 3 линий каждый отрезок делится в соотношении 2:1, считая от вершины (свойство медианы);
- из центра пересечения можно одновременно провести окружность внутри и вокруг фигуры;
- линии, делящие на равные части внешние углы правильного треугольника, параллельны противоположно расположенным сторонам фигуры;
- все 3 отрезка, проведенные из вершин, равны по длине.
Это интересно! Урок геометрии: как найти по формуле периметр треугольника
Наиболее простая формула, определяющая, как найти биссектрису треугольника, выражается через радиус вписанной (r) или описанной (R) окружности:
- l=3r;
- l=3R/2.
Характеристика внутренних линий
 Основное свойство биссектрисы треугольника с равными боковинами: отрезок, опущенный из вершины, одновременно является медианой, высотой.
Основное свойство биссектрисы треугольника с равными боковинами: отрезок, опущенный из вершины, одновременно является медианой, высотой.
При этом, кроме разделения угла на 2 равные части, линия характеризуется следующими качествами:
- делит нижнее основание пополам;
- служит перпендикуляром к противолежащей стороне;
- отрезок луча, разделяющий внешний угол вершины с равными боковинами, параллелен основанию.
Важно! Биссектрисы равных углов у основания также равны между собой по длине.
При этом верно обратное утверждение: когда 2 биссектрисы равны между собой, то треугольник считается равнобедренным.
Если вершина содержит 90° (прямой угол), то отрезки, опущенные на катеты, пересекаются под 45°. В этом случае определить размер искомого отрезка помогает теорема Пифагора.
Это интересно! Что значит вертикально и как выглядит вертикальная линия
Пример
 В треугольнике АВС вершина А содержит 90°. Отрезок АД служит высотой, биссектрисой и медианой одновременно. Образованы 2 прямоугольные трехсторонние фигуры: АВД и АСД, у которых равны основания (ВД=СД). Требуется найти длину отрезка АД.
В треугольнике АВС вершина А содержит 90°. Отрезок АД служит высотой, биссектрисой и медианой одновременно. Образованы 2 прямоугольные трехсторонние фигуры: АВД и АСД, у которых равны основания (ВД=СД). Требуется найти длину отрезка АД.
По теореме Пифагора АД2 = АВ2-ВД2. Отсюда АД = √АВ2-ВД2.
Это интересно! Изучаем символы: как обозначается в математике площадь
Соотношение со сторонами треугольника
Слово, в переводе с латинского языка, обозначает «сечение поперек». Чем отличается биссектриса от других главных и второстепенных отрезков треугольной фигуры, было известно еще Архимеду, который в своих трудах активно использовал ее свойства для определения сторон многоугольников. При этом количество сторон должно быть кратным трем. Классическая теорема о биссектрисе гласит, что линия разделяет противоположную сторону на 2 отрезка, отношение которых друг к другу такое же, как соотношение двух соприкасающихся к основанию сторон.
Пример
 Дан треугольник АВС. Из вершины А проведена биссектриса АД, разделяющая сторону ВС на 2 отрезка (ДВ и ДС). Смысл теоремы сводится к равенству нескольких величин: ВД/АВ=СД/АС и ВД/ДС=АВ/АС. Лучше понять формулу помогает фото треугольника с проведенной линией.
Дан треугольник АВС. Из вершины А проведена биссектриса АД, разделяющая сторону ВС на 2 отрезка (ДВ и ДС). Смысл теоремы сводится к равенству нескольких величин: ВД/АВ=СД/АС и ВД/ДС=АВ/АС. Лучше понять формулу помогает фото треугольника с проведенной линией.
Характеристика линий:
- любая биссектриса, выпущенная из вершины неправильного треугольника, расположена между медианой и высотой, выходящей из этого же места;
- все точки, расположенные на отрезке, удалены от сторон по бокам вершины на одинаковое расстояние;
- лучи, разделяющие пополам внешний и внутренний угол треугольной фигуры, перпендикулярны между собой;
- все отрезки, делящие на равные части внутренние углы, пересекаются в строго определенной точке, которая служит центром вписанной в эту фигуру окружности;
- если две биссектрисы равны по длине, то фигура – равнобедренная, если все одинакового размера, треугольник – правильный.
Способы построения
 Зная, что такое биссектриса, легко определить расположение отрезка в треугольной фигуре. Для построения применяется несколько способов:
Зная, что такое биссектриса, легко определить расположение отрезка в треугольной фигуре. Для построения применяется несколько способов:
- Известен угол, из которого исходит прямая, делящая его на равные сегменты. Значение делится пополам. На рисунке с помощью транспортира строится нужный отрезок.
- Если параметры угла неизвестны, его измеряют транспортиром, делят пополам, затем проводят искомую линию.
- Оригинальный способ построить нужный отрезок с помощью карандаша, линейки и циркуля. Из любой вершины проводится окружность произвольного радиуса. Главное, что величина должна быть меньше, чем прилегающая сторона. Место пересечения с каждой стороной считается центром для еще двух окружностей с таким же шагом циркуля. Нарисовать еще два круга, которые пересекаются между собой два раза. Через полученные точки и вершину под линейку проводится прямая, которая и есть настоящая биссектриса внутреннего угла.
- Построить треугольник по известной длине трех отрезков (АВ, ВС, АС) можно с помощью линейки и циркуля. На произвольной прямой линии обозначить сегмент, равный АВ. Из точки А провести окружность с шагом циркуля равным АС, а затем аналогично из точки В провести окружность с шагом ВС. Точка пересечения – вершина искомой треугольной фигуры (С), в которой легко определяются биссектрисы, учитывая их характеристики.
Важно! Если известны только размеры биссектрис, то построить по данным параметрам возможно бесконечное количество подобных фигур.
Полезное видео
Подведем итоги
Зная значение и характеристики главных линий в треугольной фигуре, можно решать много задач, определять величину углов, длину, изучать соотношение сторон.
