Загрузить PDF
Загрузить PDF
Угол можно разделить пополам так же, как отрезок. Разделить пополам – это значит разделить что-то на две равные части. Существуют два способа разделить угол пополам. Можно воспользоваться транспортиром, если он есть и если нужно измерить величину угла. Или можно провести биссектрису с помощью линейки и циркуля.
-
1
Измерьте угол. Совместите начало отсчета прямолинейной шкалы транспортира с вершиной угла, а линейку транспортира с одним из лучей угла. Посмотрите на цифру, с которой совпадает другой луч угла. Так вы найдете величину угла.
- Например, угол равен 160 градусов.
- Обратите внимание, что на полукруглой части транспортира есть две угломерные шкалы. Чтобы выяснить, какое число выбрать, подумайте об угле. Тупые углы больше 90 градусов, а острые углы меньше 90 градусов.
-
2
Разделите величину угла пополам. Биссектриса делит угол на две равные части.[1]
Поэтому, чтобы найти угол, под которым проходит биссектриса, разделите величину угла (в градусах) на 2.[2]
- Например, если угол равен 160 градусов, вычисления нужно записать так: . Таким образом, биссектриса проходит под углом 80 градусов.
- Например, если угол равен 160 градусов, вычисления нужно записать так:
-
3
Отметьте угол, под которым проходит биссектриса. Совместите начало отсчета прямолинейной шкалы транспортира с вершиной угла, а линейку транспортира с одним из лучей угла. Отметьте угол, равный половине данного угла, то есть поставьте точку между лучами данного угла.
- Например, биссектриса данного угла, который равен 160 градусов, проходит через значение в 80 градусов, поэтому поставьте точку напротив цифры 80 на транспортире и между лучами угла.
-
4
Проведите прямую из вершины угла к поставленной точке. Для этого воспользуйтесь линейкой транспортира. Проведенная прямая – это биссектриса угла.[3]
Реклама
-
1
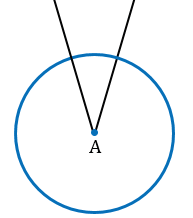
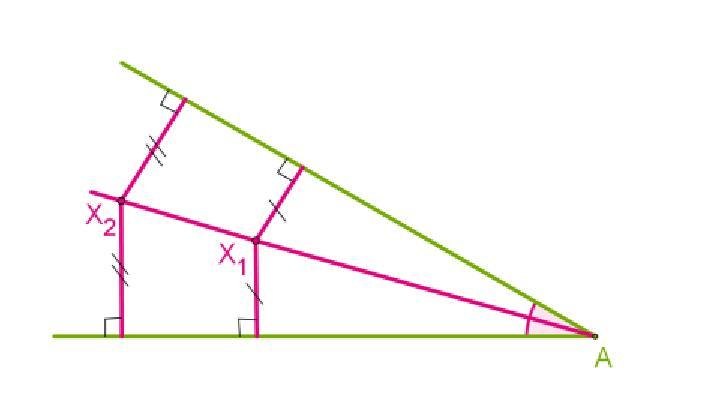
Проведите дугу, пересекающую оба луча данного угла. Раствор циркуля сделайте любым, а затем установите иглу циркуля в вершине угла. Проведите дугу так, чтобы она пересекла оба луча угла.[4]
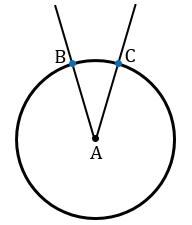
- Например, дан угол BAC. Поставьте иглу циркуля в точке А. Поверните циркуль так, чтобы нарисовать дугу, которая пересечет луч AB в точке D, а луч AC в точке Е.
-
2
Проведите первую внутреннюю дугу. Поставьте иглу циркуля в точке пересечения большой дуги и первого луча. Проведите короткую дугу между лучами угла.[5]
- Например, установите иглу циркуля в точке D и нарисуйте дугу внутри угла.
-
3
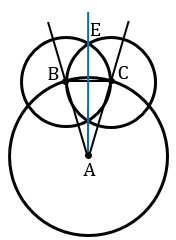
Проведите вторую внутреннюю дугу, которая пересечет первую внутреннюю дугу. Раствор циркуля не меняйте. Поставьте иглу циркуля в точке пересечения большой дуги и второго луча. Проведите вторую короткую дугу между лучами угла.[6]
- Например, установите иглу циркуля в точке Е и нарисуйте вторую дугу внутри угла. Точку пересечения двух коротких дуг обозначьте как F.
-
4
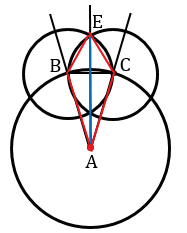
Проведите прямую из вершины угла к точке пересечения внутренних дуг. Для этого воспользуйтесь линейкой. Проведенная прямая – это биссектриса угла.[7]
- Например, с помощью линейки проведите прямую, соединяющую точки F и A.
Реклама
Об этой статье
Эту страницу просматривали 118 704 раза.
Была ли эта статья полезной?
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Построения циркулем и линейкой
- Построение биссектрисы угла
Пример:
Построить биссектрису данного угла.
Дано: 
А.
Построить: биссектрису А.
Решение:
Произвольно строим с помощью линейки А.
С помощью циркуля строим окружность произвольного радиуса с центром в вершине А.
Точки пересечения данной окружности со сторонами А обозначим В и С.
Теперь проведем две окружности одинакового радиуса ВС с центрами в точках В и С.
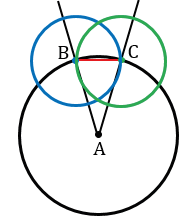
В зависимости от длины ВС, получим одну или две точки пересечения данных окружностей внутри А. Ту точку, которая лежит внутри угла обозначают буквой и проводят через нее луч с началом в точке А. В нашем случае, получилось две точки пересечения данных окружностей, которые лежат внутри А. Обозначаем одну из них Е и проводим с помощью линейки луч АЕ.
Докажем, что луч АЕ является биссектрисой данного А. Рассмотрим треугольники АВЕ и АСЕ.
В данных треугольниках АВ = АС как радиусы окружности с центром в точке А, ВЕ = СЕ по построению, АЕ – общая, следовательно,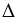 
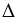
АВЕ =АСЕ по 3 признаку равенства треугольников, откуда следует, что ВАЕ =САЕ, т.е луч АЕ – биссектриса данного А. Что и требовалось доказать.
Замечание:
- С помощью циркуля и линейки можно разделить данный угол на два равных угла, для этого нужно провести его биссектрису.
- С помощью циркуля и линейки можно разделить данный угол на четыре равных угла, для этого нужно разделить угол пополам (на два равных угла), а затем каждую половину разделить пополам еще раз.
- С помощью циркуля и линейки нельзя разделить данный угол на три равных угла (задача о трисекции угла).
Советуем посмотреть:
Построение угла, равного данному
Построение перпендикулярных прямых
Построение середины отрезка
Среднее пропорциональное
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 152,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 154,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 175,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 288,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 289,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 317,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 321*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 358,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 688,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1100,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Как построить биссектрису треугольника
Треугольник и его построения имеют важное значение в начальной геометрии. Одно из построений треугольника – биссектриса – представляет собой прямой отрезок, исходящий из одной вершины треугольника и соединяющийся с точкой на противолежащем ребре. При этом биссектриса делит пополам угол данной вершины. В общем случае построение биссектрисы треугольника сводится к проведению биссектрисы угла конкретной вершины. Это построение выполняется с помощью транспортира. Однако построение биссектрисы равнобедренного и правильного треугольников можно провести с учетом их геометрических свойств без дополнительных инструментов.
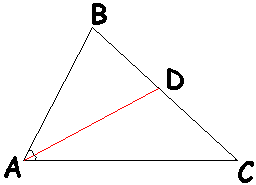
Вам понадобится
- Транспортир, линейка
Инструкция
Постройте заданный треугольник. Возьмите транспортир и измерьте угол вершины, из которой необходимо провести биссектрису. Поделите данный угол пополам.
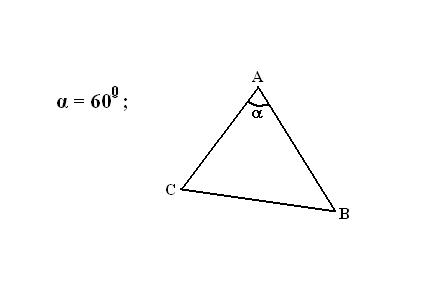
Отмерьте от стороны треугольника, прилегающей к данной вершине, высчитанный угол. Поставьте точку, обозначающую половину угла вершины.
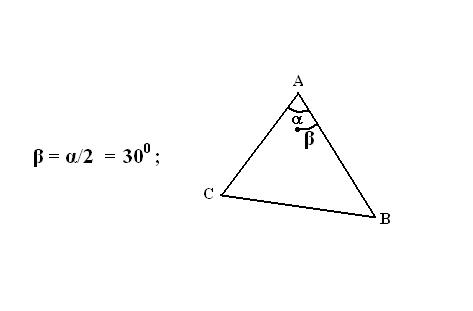
Проведите через вершину и отмеченную точку прямую линию так, чтобы она ограничивалась вершиной с одной стороны и противолежащей стороной треугольника с другой. Биссектриса треугольника построена.
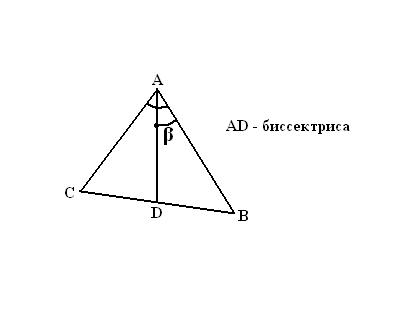
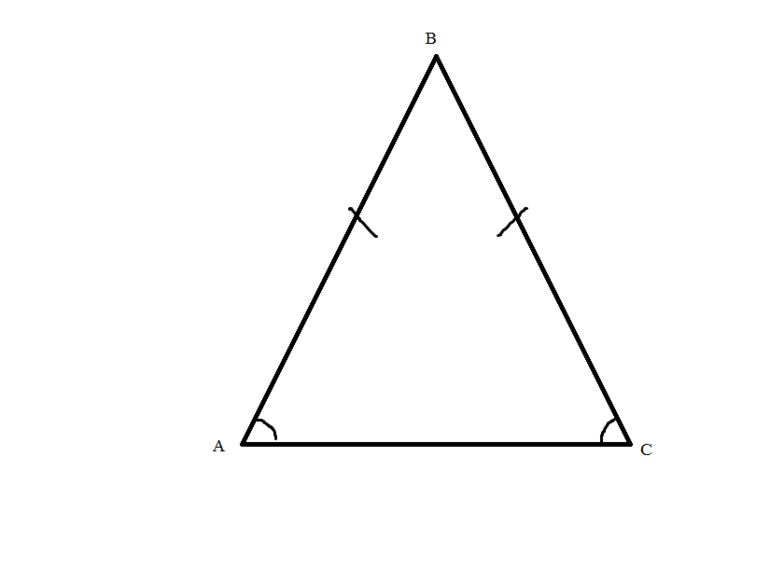
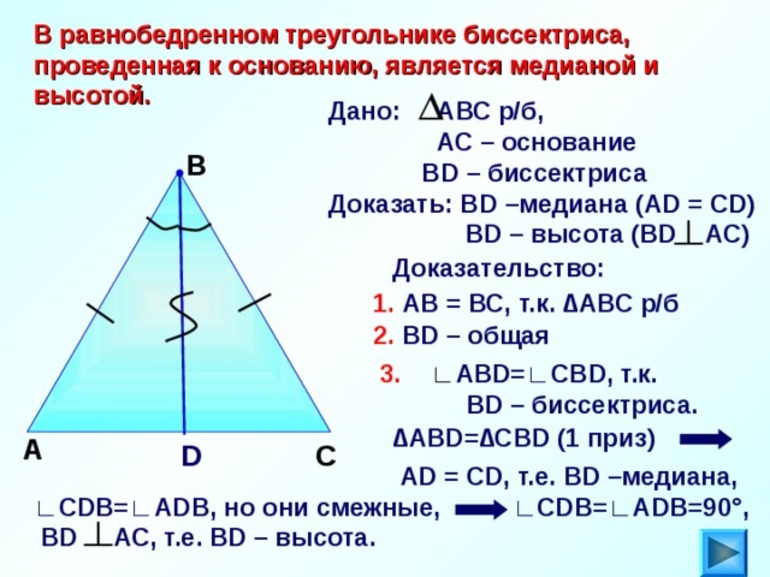
Если заданный треугольник является равнобедренным или правильным, то есть у него
равны две или три стороны, то его биссектриса, согласно свойству треугольника, будет являться также и медианой. А, следовательно, противолежащая сторона будет делиться биссектрисой пополам.
Измерьте линейкой противолежащую строну треугольника, куда будет стремиться биссектриса. Поделите данную строну пополам и поставьте в середине стороны точку.
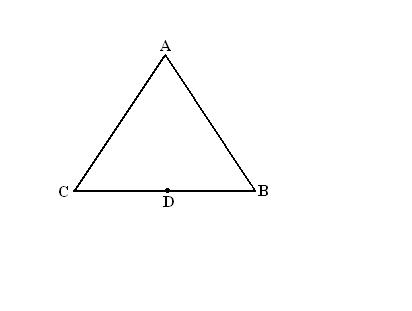
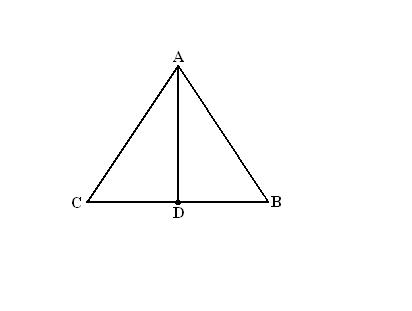
Проведите прямую линию, проходящую через построенную точку и противолежащую вершину. Это и будет биссектриса треугольника.
Источники:
- Медианы, биссектрисы и высоты треугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как построить биссектрису данного угла? Задачи на построение
Существует такой забавный детский стишок, с помощью которого легко запомнить, что такое биссектриса: “Биссектриса – это такая крыса, что бегает по углам и делит угол пополам”. Однако нельзя забывать, что, несмотря на простоту запоминания этого шуточного определения, учитель справедливо потребует другое, взятое из учебника.
В дальнейшем изучении школьной программы дети сталкиваются со сложной с первого взгляда задачей – как построить биссектрису данного угла с помощью циркуля. Однако уже более продвинутый школьник без труда справится с этим заданием, которое является основой выполнения цикла задач на построение в геометрии. Давайте же разберемся с этим вопросом раз и навсегда.
Как построить биссектрису данного угла?
Вам будет интересно: Французский язык: спряжение vivre
Самым очевидным и наиболее простым способом является использование транспортира, но если данного вспомогательного инструмента не оказалось под рукой, надо уметь строить биссектрису без него.
Для выполнения данной задачи, как уже понял читатель, нам потребуется циркуль, а помимо него – линейка (важно понимать, что делениями на ней пользоваться нельзя) и простой карандаш с ластиком.
Алгоритм построения
Необходимо совершить такие действия:
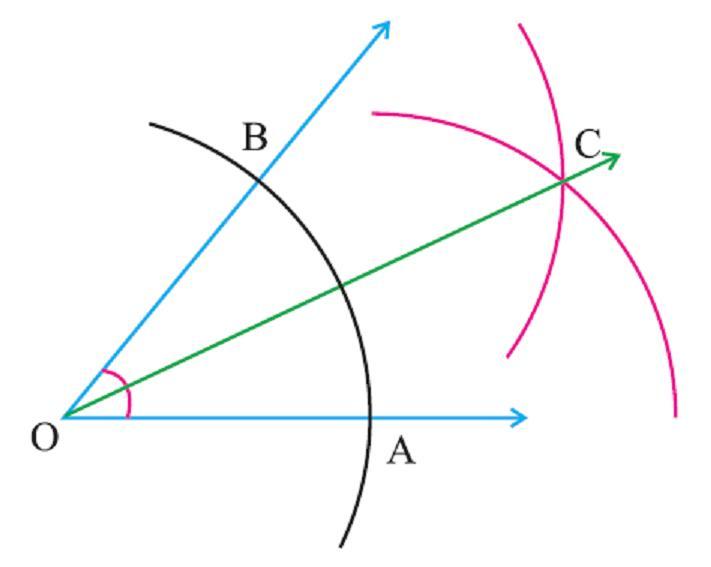
Мы дали ответ на поставленный вопрос – как построить биссектрису данного угла.
Доказательство
Теперь, разобравшись, как построить биссектрису данного угла, стоит вспомнить еще одно определение биссектрисы, используя термин “геометрическое место точек”. Биссектрисой называется геометрическое место точек, которые равноудалены от лучей, образующих угол.
Согласно выполненному построению в пунктах 4-6, точка, принадлежащая построенной биссектрисе, также принадлежит двум окружностям, равным по радиусу, центр которых располагается на лучах, образующих угол на одинаковом расстоянии от вершины угла (согласно пунктам 1-3 построения). Опустим перпендикуляр из отмеченной в пункте 6 точки на лучи, образующие угол. Докажем, что получившиеся прямоугольные треугольники равны, и выясним, что опущенные перпендикуляры также равны, как соответствующие элементы треугольников. Таким образом, их общая гипотенуза является биссектрисой угла по определению. Что и требовалось доказать.
Построить биссектрису данного угла
Скачать
презентацию
Рассмотрим треугольники АСЕ и АВЕ >>
Задача. Построить биссектрису данного угла. Решение Данный угол ВАС изображен на рисунке. Проведем окружность произвольного радиуса с центром в вершине А. Она пересечет стороны угла в точках В и С. Затем проведем две окружности одинакового радиуса ВС с центрами в точках B и С. Они пересекутся в двух точках. Ту из этих точек, которая лежит внутри угла ВАС, обозначим буквой Е. Докажем, что луч АЕ является биссектрисой данного угла ВАС.
Слайд 9 из презентации «Геометрические задачи на построение». Размер архива с презентацией 2014 КБ.
Геометрия 7 класс
«Начальные сведения геометрии» – Учёные- геометры. (Около 365-300 до н.э). Введение в геометрию. (1792-1856). Стереометрия. Взаимное расположение точек, прямой и отрезка. Оглавление. Евклид. Геометрические фигуры. Свойство прямой. (Около 570-500до н.э). Пифагор. Сколько точек пересечения могут иметь три прямые ? Планиметрия. Практические задания Взаимное расположение прямых на плоскости Практические задания. История возникновения геометрии.
«Параллельны ли прямые» – Рядом идущие. Вопросы. Папп. Посидоний. Замыкание. Способ построения. Свести параллели к схождению. Способ. Мужская голова. Определения параллельных прямых. Способ построения параллельных прямых. Николай Иванович Лобачевский. Недостаток информации. Построения параллельных прямых. Прямые, лежащие в одной плоскости. Параллельные прямые. Значимость параллельных прямых. Гипотеза. Аксиома параллельных прямых.
«1 признак равенства треугольников» – Равенство треугольников. Историческая справка. Какое еще условие должно быть выполнено. Треугольники, изображенные на рисунке. Ребусы. Треугольники АВС и ACD равны. Треугольники, изображенные на рисунке, равны. Треугольник. Треугольники равны. Первый признак равенства треугольников. Тестирование. Цели урока. Минутка отдыха. План урока. Самостоятельная работа. Найдите по рисунку величину угла АDС и длину стороны ВС.
«Геометрические задачи на построение» – Отложить от данного луча угол, равный данному. Рассмотрим треугольники АВС и ОDЕ. Через вершину угла А и точку пересечения окружностей Е проведем прямую. Практические задания по группам. Построение перпендикулярных прямых. Строка параметров включает в себя кнопки состояния полей и сами поля. Медиана РМ равнобедренного треугольника. Построение прямоугольника в ручном режиме. Построить окружность с центром в точке В и с радиусом АВ.
«Свойства и признаки равнобедренного треугольника» – Установка. Равнобедренный треугольник. Медианы. Найдите угол. Девиз нашего урока. Биссектриса треугольника. Контрольные вопросы. Биссектрисы. Две стороны и угол между ними. Два перпендикуляра. Построение циркулем и линейкой. Понятие «свойство». Равносторонний треугольник. Треугольник. Высота. Углы при основании. Качество. Сумма углов треугольника. Исследовательская работа. Свойства треугольников. Достройте треугольник своего настроения.
««Измерение углов» 7 класс» – Измерение углов. Найдите угол, образованный биссектрисами углов. Лучи с общим началом в точке О. Луч OV является биссектрисой угла ZOY. Решение задач. Измерим величину угла АОВ. Свойства углов. Решение задач по готовым чертежам. Как строятся и измеряются углы с помощью транспортира. Виды углов.
Всего в теме «Геометрия 7 класс» 55 презентаций
ПРОШУ ПОМОГИТЕ
Построить биссектрису данного неразвёрнутого угла.
Добавьте пропуски в тексте решения задачи.
Пусть дан неразвёрнутый угол А.
Проведём окружность произвольного радиуса с центром _______и обозначим точки её пересечения со сторонами угла буквами _______и С. Затем построим две окружности радиуса _______ с центрами _______ и С.
Они пересекутся в двух точках. Ту из точек пересечения окружностей, которая лежит с точкой A по разные стороны от прямой BC, обозначим буквой _______. Наконец, проведём луч _______.Это и есть искомая биссектриса данного угла A.
Доказательство
В самом деле, треугольники ABD и _______равны по _______ (AB = _______, BD = _______, _______ ─ общая сторона). Поэтому ∠ BAD = ∠ _______, т.е. луч _______ ─ биссектриса угла _______.
[spoiler title=”источники:”]
http://5klass.net/geometrija-7-klass/Geometricheskie-zadachi-na-postroenie/009-Postroit-bissektrisu-dannogo-ugla.html
http://znanija.org/geometriya/36917378.html
[/spoiler]
Процесс построения
Биссектриса (лат. bisectio) представляет собой геометрическое место точек внутри угла (острый, прямой или тупой), которые одинаково удалены от обеих его сторон.
Для её построения нужно подготовить различные школьные принадлежности и выполнить несколько простых действий.
Подготовительный этап
Чтобы быстро найти биссектрису треугольника с помощью циркуля, нужно провести тщательную подготовку. Она заключается в поиске школьных принадлежностей, которые будут использоваться при построении.
Необходимые предметы:
- простой карандаш;
- линейка;
- ластик;
- циркуль;
- лист бумаги.
Порядок действий
Нарисовать луч, разделяющий пополам угол, можно при помощи транспортира. Однако если этой школьной принадлежности нет в наличии, заменить её сможет обыкновенный циркуль.
Быстрый способ:
- На листе бумаги рисуют 2 пересекающиеся линии.
- Чтобы построить биссектрису данного угла, в его вершину ставят ножку циркуля и чертят окружность произвольного радиуса.
- Отмечают точками места пересечения сторон угла с окружностью.
- На них поочерёдно ставят циркуль и, не меняя радиус, рисуют 2 дуги.
- Находят и отмечают место их пересечения.
- Стирают дуги ластиком, чтобы они не мешали дальнейшей работе.
- С помощью линейки и простого карандаша проводят искомый отрезок, соединяющий вершину угла с точкой пересечения дуг.
С помощью циркуля можно легко найти биссектрису треугольника (всякого). Для этого понадобится стандартный набор школьных принадлежностей и наличие базовых знаний геометрии.
Порядок действий:
- Любым известным способом вписывают окружность в треугольник.
- С помощью карандаша и линейки из её центра проводят линии к каждой вершине.
- Полученные отрезки станут частью искомого луча.
Альтернативный вариант
Если у ученика нет циркуля, то начертить луч, разделяющий угол пополам, можно и без этой школьной принадлежности. Для работы понадобится линейка, карандаш и транспортир.
Правильная последовательность действий:
- Нулевое значение на шкале прикладывают к вершине.
- Совмещают линейку транспортира с одним из лучей и определяют величину угла.
- Полученное значение делят пополам.
- Затем заново прикладывают транспортир и откладывают величину, полученную в результате расчётов.
- Через эту точку и вершину проводят отрезок, который будет являться искомым лучом.
Полезные советы
В некоторых случаях для нахождения не нужно использовать транспортир и циркуль. Это возможно только тогда, когда нужно определить расположение биссектрисы в треугольнике.
Полезные рекомендации:
- Биссектриса всегда разделяет противолежащую сторону треугольника в отношении, равном пропорции 2 других сторон геометрической фигуры.
- В равнобедренном треугольнике биссектрисы всегда пересекаются под прямым углом.
- Если треугольник равносторонний, то все биссектрисы будут параллельны противоположным сторонам. При этом длина образованных отрезков будет одинаковой.
Построить биссектрису угла с помощью циркуля сможет даже двоечник. Для этого ему понадобится минимум времени, знаний и усилий. Подробно изучив порядок действий, каждый учащийся сможет легко поделить любой угол пополам и объяснить этот процесс одноклассникам.
