Как найти биссектрису угла квадрата - Сайт, где вы сможете решить свои вопросы

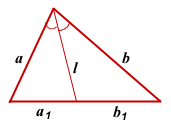
Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.

I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.

Утверждение 1

Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

$[ l = sqrt {ab - a_1 b_1 } ]$

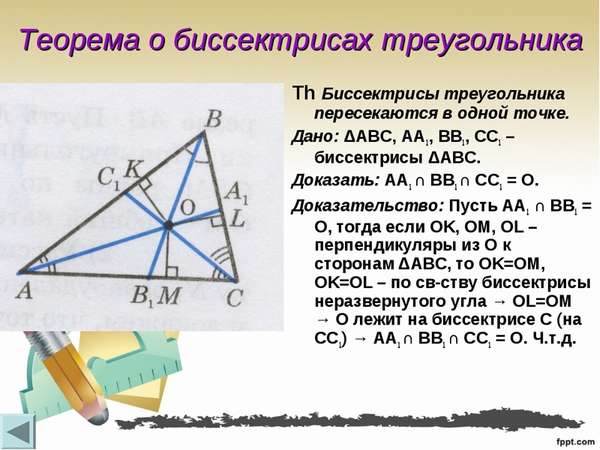
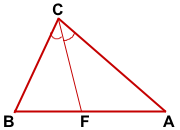Дано:

ΔABC,

СF — биссектриса ∠ABC

Доказать:

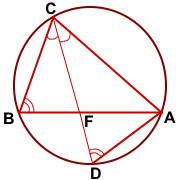Доказательство:

Опишем около треугольника ABC окружность и продлим биссектрису CF до пересечения с окружностью в точке D. Соединим точки A и D отрезком.

Рассмотрим треугольники BCF и DCA.

∠BCF=∠DCA (по условию);

∠CBF=∠CDA (как вписанные углы, опирающиеся на одну дугу AC).

Значит, треугольники BFC и DCA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

$[ frac{{BC}}{{CD}} = frac{{CF}}{{AC}}, Rightarrow CD = frac{{BC cdot AC}}{{CF}}. ]$

$[ FD = CD - CF = frac{{BC cdot AC}}{{CF}} - CF. ]$

По свойству пересекающихся хорд

Отсюда

$[ BF cdot AF = CF cdot (frac{{BC cdot AC}}{{CF}} - CF) ]$

Что и требовалось доказать.

II. Через три стороны треугольника

Утверждение 2

Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле

$[ l_c = frac{1}{{a + b}}sqrt {ab(a + b + c)(a + b - c)} . ]$

Доказательство:

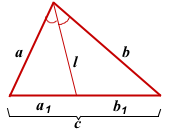По свойству биссектрисы треугольника:

$[ [ frac{a}{{a_1 }} = frac{b}{{b_1 }}, Rightarrow a_1 b = ab_1 . ]$

a₁+b₁=c, b₁=c-a₁, поэтому

$[ a_1 = frac{{ac}}{{a + b}}. ]$

Согласно утверждению 1,

$[ l^2 = ab - a_1 (c - a_1 ) = ab - frac{{ac}}{{a + b}}(c - frac{{ac}}{{a + b}}) = ]$

$[ = ab - frac{{ac^2 }}{{a + b}} + frac{{a^2 c^2 }}{{(a + b)^2 }} = frac{{ab(a + b)^2 - ac^2 (a + b) + a^2 c^2 }}{{(a + b)^2 }} = ]$

$[ = frac{{ab(a + b)^2 - a^2 c^2 - abc^2 + a^2 c^2 }}{{(a + b)^2 }} = frac{{ab(a + b)^2 - abc^2 }}{{(a + b)^2 }} = ]$

$[ = frac{{ab}}{{(a + b)^2 }}((a + b)^2 - c^2 ) = frac{{ab}}{{(a + b)^2 }}((a + b) + c)((a + b) - c) = ]$

$[ = frac{{ab}}{{(a + b)^2 }}(a + b + c)(a + b - c), ]$

откуда

$[ l = sqrt {frac{{ab}}{{(a + b)^2 }}(a + b + c)(a + b - c)} , ]$

$[ l_c = frac{1}{{a + b}}sqrt {ab(a + b + c)(a + b - c)} . ]$

Что и требовалось доказать.

Аналогично,

$[ l_a = frac{1}{{b + c}}sqrt {bc(b + c + a)(b + c - a)} , ]$

$[ l_b = frac{1}{{a + c}}sqrt {ac(a + c + b)(a + c - b)} . ]$

III Через две стороны треугольника и угол между ними.

Утверждение 3

Длина биссектрисы треугольника через две стороны, образующие угол, из вершины которого исходит биссектриса, и угол между этими сторонами выражается по формуле

$[ l_c = frac{{2abcos frac{alpha }{2}}}{{a + b}} ]$

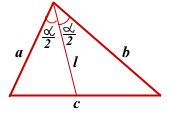
Доказательство:

Найдем площади треугольников BCF, ACF и ABC.

$[ S_{Delta BCF} = frac{1}{2}BC cdot CF cdot sin angle BCF, ]$

$[ S_{Delta ACF} = frac{1}{2}AC cdot CF cdot sin angle ACF, ]$

$[ S_{Delta ABC} = frac{1}{2}AC cdot BC cdot sin angle BCA. ]$

Так как

$[ S_{Delta ABC} = S_{Delta BCF} + S_{Delta ACF} , ]$

то

$[ frac{1}{2}AC cdot BC cdot sin angle BCA = ]$

$[ = frac{1}{2}BC cdot CF cdot sin angle BCF + frac{1}{2}AC cdot CF cdot sin angle ACF, ]$

$[ ab cdot sin alpha = al cdot sinfrac{alpha }{2} + bl cdot sinfrac{alpha }{2}, ]$

$[ ab cdot sin alpha = l cdot sinfrac{alpha }{2}(a + b), ]$

$[ l = frac{{ab cdot sin alpha }}{{sinfrac{alpha }{2}(a + b)}} = frac{{ab cdot sin (2 cdot frac{alpha }{2})}}{{sinfrac{alpha }{2}(a + b)}} = frac{{ab cdot 2sin frac{alpha }{2}cos frac{alpha }{2}}}{{sinfrac{alpha }{2}(a + b)}} = frac{{2abcos frac{alpha }{2}}}{{a + b}}. ]$

Что и требовалось доказать.

Источник

Биссектрисы квадрантов

protection click fraud

Декартова плоскость образована двумя перпендикулярными осями, которые пересекаются в начале координат (0,0), образуя четыре квадранта. Перпендикулярное пересечение осей образует углы 90 °.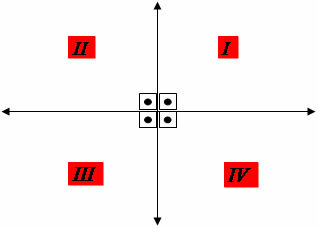

В декартовой плоскости, когда мы проводим прямую линию, которая проходит через точку (0,0), образуя угол 45º. абсциссой (горизонтальная ось) делим квадрант пополам и определяем его биссектриса.
Мы можем проследить биссектрисы квадрантов двумя способами: биссектрисы четных квадрантов и биссектрисы нечетных квадрантов.
Биссектриса нечетных квадрантов
Биссектриса нечетных квадрантов определяется прямой линией, которая пересекает точку (0,0), отслеживая биссектрисы квадрантов I и III.

Уклон будет равен m = tg 45 ° = 1. Одна из его точек будет (0,0), а все остальные точки, принадлежащие прямой b, будут иметь ординаты и абсциссы, равные, например, (4,4), (5,5), (6.6), (7, 7),…
Принимая во внимание любую из этих точек и наклон равным 1, мы можем заключить, что линия, представляющая биссектриса нечетных квадрантов будет иметь – согласно концепциям аналитической геометрии – фундаментальное уравнение: y – y0 = m (х – х0).

Подставляя точку (2.2), имеем:
у – 2 = 1 (х – 2)
у – 2 = х – 2
у = х
Биссектриса четных квадрантов

Биссектриса четных квадрантов определяется прямой линией, которая пересекает точку (0,0), отслеживая биссектрисы квадрантов II и IV.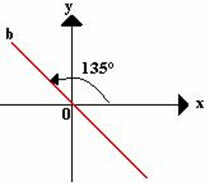

Уклон будет равен m = tg 135 ° = -1. Одна из его точек будет (0,0), а все остальные точки, принадлежащие линии b, будут иметь значения ординат, противоположные значениям абсцисс, например, (4, -4), (5, -5), (6, -6), (7, -7),…
Принимая во внимание любую из этих точек и наклон равный -1, мы можем заключить, что линия, представляющая биссектриса четных квадрантов будет иметь – согласно концепциям аналитической геометрии – фундаментальное уравнение: y – y0 = m (x – х0).
y – (–2) = –1 (x – 2)
y + 2 = –x + 2
у = – х

Марк Ноа
Окончил математику
Бразильская школьная команда

Аналитическая геометрия – Математика – Бразильская школа

Источник: Бразильская школа – https://brasilescola.uol.com.br/matematica/as-bissetrizes-dos-quadrantes-1.htm

Teachs.ru

Источник

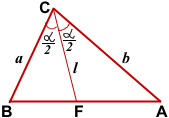
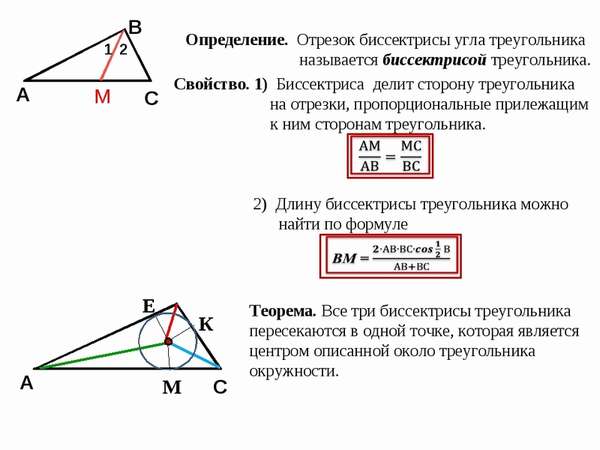
Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

CD – внутренняя биссектриса ∠ACB;
CE – биссектриса угла, смежного с ∠ACB;
∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Вычисление биссектрисы треугольника с известными свойствами

Математика, как известно, царица наук. Неслучайно это выражение так любят учителя, особенно старой формации. Математика открывается исключительно тем, кто умеет, во-первых, логически мыслить, а во-вторых, тем, кто любит всегда добиваться ответа, оперируя изначальными условиями, не жульничая, а основывая решения на анализе, построение опять-таки логических связей. Эти качества, вынесенные со школьной скамьи, способны модулироваться и к взрослой серьезной жизни как в рабочих, так и в иных сложных моментах.

Свойства
Свойства в равнобедренных треугольниках
Определение биссектрисы треугольника
Определение длины
Нахождение величины угла

Сегодня многие сталкиваются с проблемами при решении математических задач еще в начальной школе.

Однако даже те школьники, которые успешно осваивают первичную математическую программу, переходя на новый школьный и жизненный этап, где алгебра отделяется от геометрии, бывает, сталкиваются с серьезными затруднениями. Между тем, один раз выучив и, главное, поняв, как найти биссектрису треугольника, ученик навсегда запомнит эту формулу. Рассмотрим треугольник ABC с тремя проведенными биссектрисами. Как видно из рисунка, все они сходятся в одной точке.

Во-первых, определим, что биссектриса треугольника, и это одно из важнейших ее свойств, делит угол, из которого такой отрезок исходит, пополам. То есть в приведенном примере угол BAD равен углу DAC.

Это интересно: Как найти периметр треугольника.

Свойства

Биссектриса треугольника разделяет сторону, к которой она проведена на два отрезка, обладающие свойствами пропорциональности к сторонам, которые прилегают к каждому отрезку, соответственно. Таким образом, BD/CD = AB/AC.
Каждый треугольник способен обладать тремя данными отрезками. Другие значимые свойства касаются как частных, так и общих случаев конкретных рассматриваемых треугольников.

Свойства в равнобедренных треугольниках

Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
Разумеется, что будет верным и обратное свойство. То есть в равнобедренном треугольнике неизменно наблюдается равенство двух его биссектрис.
Из сказанного ранее вытекает вывод о том, что биссектриса, исходящая из противоположного основанию, служит также медианой и высотой.
Все биссектрисы равностороннего треугольника обладают равенством.

Определение биссектрисы треугольника

Допустим, что в рассматриваемом треугольнике ABC сторона AB = 5 cm, AC = 4 cm. Отрезок CD = 3 cm.

Определение длины

Определить длину можно по следующей формуле. AD = квадратный корень из разности произведения сторон и произведения пропорциональный отрезков.

Найдем длину стороны BC.

Из свойств известно, что BD/CD = AB/AC.
Значит, BD/CD = 5/4 = 1,25.
BD/3 = 5/4.
Значит, BD = 3,75.
ABxAC = 54=20.
CDxBD = 33,75 = 11,25.

Так, для того чтобы рассчитать длину, требуется вычесть из 20 11,25 и извлечь квадратный корень из получившегося 8,75. Результат с учетом тысячных долей получится 2,958.

Данный пример призван также эксплицитно указать на ситуацию, когда значения длины биссектрисы, как и все другие значения в математике, будут выражены не в натуральных числах, однако бояться этого не стоит.

Это интересно: в чем выражается эволюционный характер развития общества?

Нахождение величины угла

Для нахождения углов, образующихся биссектрисой, важно, прежде всего, помнить о сумме углов, неизменно составляющей 180 градусов. Предположим, что угол ABC равен 70 градусам, а угол BCA 50 градусам. Значит, путем простейших вычислений получим, что CAB = 180 (70+50) = 60 градусов.

Если использовать главное свойство, в соответствии с которым угол, из которого она исходит, делится пополам, получим равные значения углов BAD и CAD, каждый из которых будет 60/2 = 30 градусов.

Если требуется дополнительный наглядный пример, рассмотрим ситуацию, когда известен лишь угол BAD равный 28 градусам, а также угол ABC равный 70 градусам. Используя свойство биссектрисы, сразу найдем угол CAB путем умножения значения угла BAD на два. CAB = 282 =56. Значит, BAC = 180 (70+56) или 180 (70+282)= 180 126 = 54 градуса.

Специально не рассматривалась ситуация, когда данный отрезок выступает в качестве медианы или высоты, оставив для этого другие специализированные статьи.

Таким образом, мы рассмотрели такое понятие, как биссектриса треугольника, формула для нахождения длины и углов которой заложена и реализована в приведенных примерах, имеющих целью наглядно показать, каким образом можно использовать для решения тех или иных задач в геометрии. Также к данной теме относятся такие понятия, как медиана и высота. Если данный вопрос прояснился, следует обращаться к дальнейшему изучению различных других свойств треугольника, без которых немыслимо дальнейшее изучение геометрии.

Биссектриса треугольника

Длина биссектрисы треугольника

Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.

I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.

Дано:

СF — биссектриса ∠ABC

Доказательство:

Рассмотрим треугольники BCF и DCA.

∠BCF=∠DCA (по условию);

Значит, треугольники BFC и DCA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Что и требовалось доказать.

II. Через три стороны треугольника

Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле

По свойству биссектрисы треугольника:

Согласно утверждению 1,

Что и требовалось доказать.

III Через две стороны треугольника и угол между ними.

[spoiler title=”источники:”]

http://tvercult.ru/nauka/vyichislenie-bissektrisyi-treugolnika-s-izvestnyimi-svoystvami

Длина биссектрисы треугольника

[/spoiler]

Источник

Библиографическое описание:

Магомедов, С. А. Ещё раз о квадрате длины биссектрисы в произвольном треугольнике / С. А. Магомедов, В. В. Акопов. — Текст : непосредственный // Юный ученый. — 2021. — № 4 (45). — С. 8-12. — URL: https://moluch.ru/young/archive/45/2431/ (дата обращения: 23.05.2023).

В

данной статье рассматривается вывод формулы квадрата длины биссектрисы в произвольном треугольнике. Вывод формулы разными способами даёт возможность учащимся повторить широкий спектр геометрических фактов, совершенствовать навыки применения разных методов и приёмов решения задач, способствует более глубокому и прочному пониманию и запоминанию материала.

Ключевые слова:

биссектриса, длина, произвольный треугольник.

Математика — это искусство называть разные вещи одним и тем же именем.

А. Пуанкаре

Когда-то геометрия олицетворяла всю математику. Геометрия, как и всякая наука, возникла под влиянием жизненных потребностей. Необходимость их повседневного удовлетворения ставит человека перед целым рядом вопросов о форме окружающих его предметов, вычислениях, связанных с землемерием, строительным делом и т. д. Первые геометрические понятия возникли в доисторические времена. Человек не только пассивно наблюдал природу, но и практически осваивал и использовал её богатство. Имеются вполне достоверные сведения о значительном развитии геометрических знаний в Египте более чем за две тысячи лет до нашей эры. Материальные потребности побуждали людей изготовлять орудия труда, обтёсывать камни и строить жилища, лепить глиняную посуду и натягивать тетиву на лук. Люди натягивали свои луки, изготавливали разные предметы с прямыми рёбрами и постепенно дошли до отвлечённого понятия прямой линии. Узкая плодородная полоса земли между пустыней и рекой Нил ежегодно подвергались затоплению, и каждый раз разлив смывал границы участков, принадлежащих отдельным лицам. После спада воды требовалось с возможно большей точностью восстановить эти границы, ибо каждый из участков ценился весьма высоко. Это заставило египтян заниматься вопросами измерения, то есть землемерием. Помимо этого, они вели развитую торговлю и поэтому нуждались в умении измерять ёмкость сосудов. Искусство кораблевождения привело их к астрономическим сведениям. Выдающиеся постройки египтян — пирамиды, которые сохранились до нашего времени, свидетельствуют, что их сооружение требовало знания пространственных форм. Всё это указывает на чисто опытное происхождение геометрии.

Практическая деятельность человека служила основой длительного процесса выработки отвлечённых понятий, открытия простейших геометрических зависимостей и соотношений. Со времён, когда накопилось большое количество геометрических фактов, у людей появилась потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Геометрия стала наукой лишь после появления в ней теорем и доказательств.

К числу основных геометрических фактов следует отнести и теорему о квадрате длины биссектрисы угла произвольного треугольника. Эта теорема часто используется при решении геометрических задач.

Биссектриса это очень интересная, удивительная и замечательная линия в треугольнике. Поэтому и к числу основных геометрических фактов следует отнести и теорему о том, что биссектриса делит противоположную сторону треугольника в отношении прилежащих сторон.

Из различных источников Интернета известна формула квадрата длины биссектрисы произвольного треугольника (рис.1):

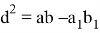
. Теорема интересна тем, что существует три способа (метода) её доказательства:

Через вписанные углы.
Через теорему косинусов.
Через теорему Стюарта.

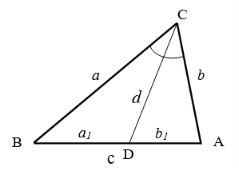
Рис. 1

Предлагается четвёртый способ доказательства этой теоремы.

Теорема.

Квадрат длины биссектрисы произвольного треугольника равен разности произведения образующих его сторон и произведения отрезков, на которые биссектриса делит третью сторону треугольника.

Доказательство. В произвольном ∆

АВС

биссектриса угла

С

обозначается

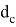
. Через стороны треугольника она выражается следующей формулой:

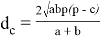
, (1)

где

p

— полупериметр.

Возведём обе части выражения (1) в квадрат и с учётом, что

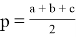
, будем иметь:

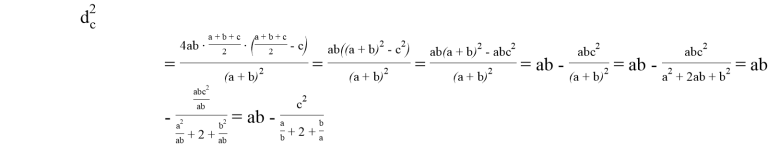
(2)

По свойству биссектрисы внутреннего угла треугольника

АВС

имеем:

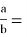
, (3)

где

a
₁

,

b
₁

— отрезки стороны

АВ=с

.

Из выражений (2) и (3) найдём квадрат биссектрисы:

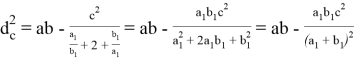
(4)

Используя выражение (4) с учётом, что

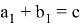
, получим:

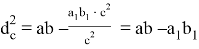
, что и требовалось доказать.

А теперь сформулируем теорему о квадрате длины биссектрисы в треугольнике иначе.

Теорема.

Квадрат длины биссектрисы треугольника равен произведению суммы двух сторон одного треугольника и разности двух сторон другого, на которые он разделён биссектрисой (рис.1):

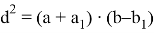
Доказательство. Воспользуемся формулой квадрата длины биссектрисы произвольного треугольника:

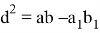
. (5)

Биссектриса

CD

делит треугольник

АВС

на два треугольника: ∆

АСD

и ∆

ВСD

. По свойству биссектрисы внутреннего угла ∆

АВС

будем иметь:

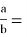
или

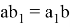
, (6)

Сложив выражения (5) и (6), получим:

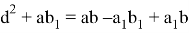
или

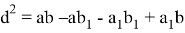
. Произведём группировку:

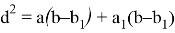
, отсюда

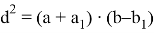
, что и требовалось доказать.

Задача 1.

В треугольнике

AВC

известно, что

a=9см, b=6см, с=12см

.

Из вершины угла

C

проведена биссектриса

CD

. Найти длину биссектрисы

CD

(рис.1).

Ответ:

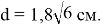
Задача 2.

В треугольнике

AВC

из вершины угла

C

проведена биссектриса

CD

, которая делит сторону

АВ

в

отношении

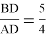
. Известно, что

d=CD=12см,a=BC=18см.

Найти длину стороны

АВ=c

(рис.1).

Ответ:

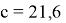
см

.

Учитель, приучая учащихся к самостоятельному поиску доказательства, поощряя их работу в этом направлении (даже, если найденное доказательство сложнее известного), может добиться более прочных и глубоких знаний, способствовать повышению интереса к предмету.

Обучение учащихся доказательству теорем зачастую оказывается малоэффективным. Одна из причин этого, на мой взгляд, отсутствие возможности у авторов школьных учебников представлять различные способы доказательства той или иной теоремы. Следовательно, для активизации познавательной деятельности учащихся и для повышения логического уровня их мышления, учителю необходимо ставить перед учащимися проблему поиска различных способов доказательства одной и той же теоремы. Учитель должен на примере показать, как это делается. Затем перед учителем возникает проблема побудить у учащихся желание самостоятельно искать различные способы доказательства теорем.

Таким образом, отыскание различных способов доказательства одной и той же теоремы — важнейшее средство развития творческого мышления учащихся.

Литература:

Выгодский М. Я. Справочник по элементарной математике. Москва. «Наука». 1986.
Некрасов В. Б. Школьная математика. Санкт-Петербург. «Авалон». 2006.
Научно-исследовательская работа по теме «Биссектриса угла треугольника». Учащийся: Александров А. А. Научный руководитель: Чуканова И. И. Республика Татарстан. Бугульма, 2012.

Источник

Являются ли диагонали биссектрисами угла квадрата?

Ученик

(159),
закрыт

7 лет назад

Дополнен 10 лет назад

..ну углов квадрата….

Михаил Иванов

Знаток

(352)

10 лет назад

Да, диагональ квадрата является биссектрисой его угла. Так как любой внутренний угол квадрата равен 90 градусам. Диагональ квадрата проходит от противолежащих его углов друг к другу и делит квадрат на два равных треугольника. Треугольники получаются прямоугольными и равнобедренными Возьмем прямоугольно-равнобедренный треугольник и просчитаем градусы углов треугольника. Их сумма равна 180 градусов. Прямой угол треугольника равен 90 градусов. Из суммы углов треугольника вычитаем этот угол и останется 90 градусов на два других угла. Треугольник равнобедренный, => два оставшихся угла равны. Делим 90 градусов на 2 и получаем по 45 градусов каждый угол. Когда эти два треугольника “склеиваются” гипотенузами, получается квадрат. Гипотенуза любого из “склеившихся” треугольников становится диагональю этого квадрата. Углы по 45 градусов с одной стороны диагонали и с другой сложились и получились прямые углы квадрата, равные 90 градусам . А как сказано выше, в любом квадрате каждый внутренний его угол равен 90 градусов. А этой ситуации диагональ делит два противолежащих угла пополам, она будет являться его биссектрисой…

Источник

Биссектрисы квадрантов

Определение и свойства биссектрисы угла треугольника

Определение биссектрисы угла треугольника

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Свойство 2

Свойство 3

Свойство 4

Свойство 5

Пример задачи

Вычисление биссектрисы треугольника с известными свойствами

Свойства

Свойства в равнобедренных треугольниках

Определение биссектрисы треугольника

Определение длины

Нахождение величины угла

Длина биссектрисы треугольника

Библиографическое описание:

Являются ли диагонали биссектрисами угла квадрата?

Вам также может понравиться

Как найти исполнительный лист по исполнительному производству

Как правильно составить бизнес план образец бесплатно для малого бизнеса ип

Как найти площадь сечения тетраэдра плоскостью

Добавить комментарий Отменить ответ