Как найти биссектрису угла между двумя прямыми

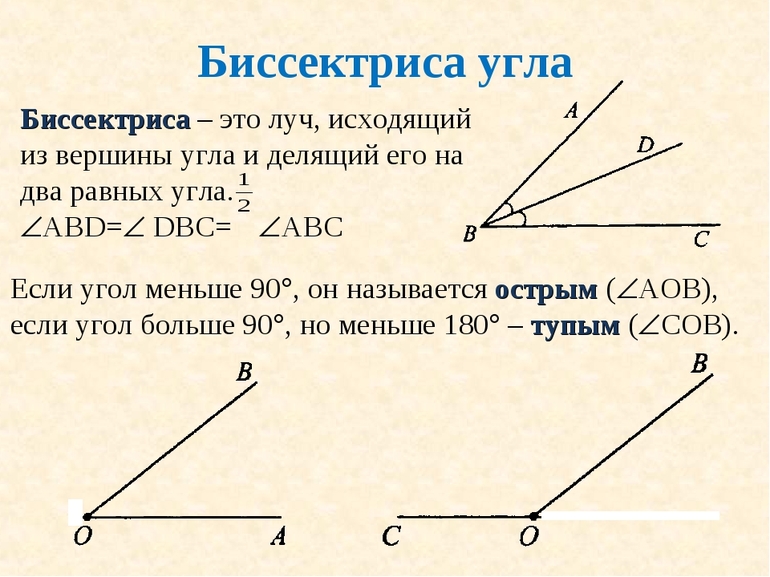
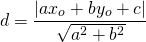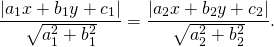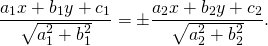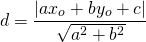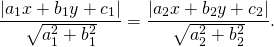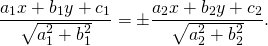Уравнение биссектрисы угла

Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.

Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0.

Расстояние от точки (x_o;y_o) до прямой ax+by+c=0 определяется по формуле

По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.

Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0, находится от этих прямых на одинаковом расстоянии, то есть

Это равенство можно записать в виде

Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.

Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.

В формулу уравнения биссектрис подставляем данные прямых:

Составить уравнение биссектрис углов образованных двумя прямыми

Составить уравнение биссектрисы острого угла между прямыми

Решение

Найдем точку пересечения двух прямых

Направляющий вектор первой прямой есть , второй , так как их скалярное произведение положительно , поэтому найдем уравнение биссектрисы между векторами , проходящую через точку

Направляющий вектор биссектрисы угла равен сумме нормированных направляющих векторов сторон

Так как точка лежит на этой биссектрисе, то

Задание 8

Составить уравнение плоскости, которая проходит через точку параллельно плоскости

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9987 – | 7776 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.

Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0.

Расстояние от точки (x_o;y_o) до прямой ax+by+c=0 определяется по формуле

По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.

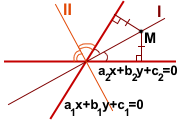
Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0, находится от этих прямых на одинаковом расстоянии, то есть

Это равенство можно записать в виде

Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.

Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.

В формулу уравнения биссектрис подставляем данные прямых:

Что ты хочешь узнать?

Ответ

Проверено экспертом

Даны прямые: 11x-2y+5=0 и 4x+8y-7=0

Уравнения биссектрис углов между прямыми Ax + By + C = 0 и A₁x + B₁y + C₁ = 0:

Знак + или – выбирается в зависимости от того, нужно уравнение биссектрисы острого или тупого углов.

Подставив коэффициенты заданных прямых в приведенную формулу, получим уравнения биссектрис:

В приближённом варианте у ≈ 1,3541х + 1,3772.

Задача 34288 Составить уравнение биссектрисы угла.

Условие

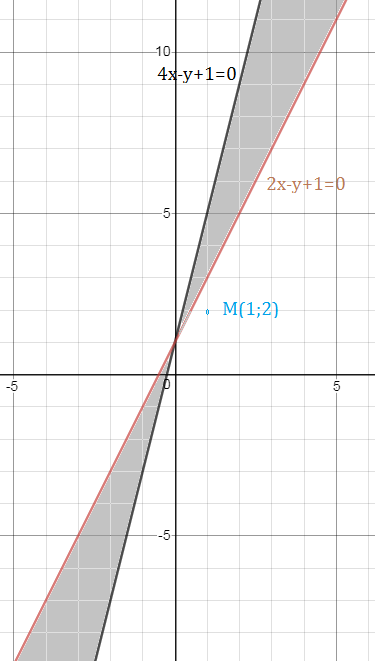
Составить уравнение биссектрисы угла между прямыми l1(4x–y+1=0) и l2(2x–y+1=0) смежного с углом, содержащим точку M(1;2)

Решение

Пусть точка Р(х;у) лежит на биссектрисе угла между прямыми.
Это значит, что расстояние d_(1) это точки до прямой l_(1) равно
расстоянию d_(2) это точки до прямой l_(2)

Прямая 4x–y+1=0 разбивает плоскость хОу на две области:
4x–y+1>0 или 4x–y+1 0 – верно;
Прямая 2x–y+1=0 разбивает плоскость хОу на две области:
2x–y+1>0 или 2x–y+1 0 – верно;

Значит точка M принадлежит области
4x–y+1>0
2x–y+1>0
а смежные области задаются неравенствами противоположных знаков.

Поэтому в (#) знак модуля раскрывается так:
(4x-y+1)/sqrt(4^2+1^2) =- (2x-y+1)/sqrt(2^2+1^2)

Делим на (sqrt(5)+sqrt(17))

((2sqrt(17)+4sqrt(5))/(sqrt(17)+sqrt(5))) * x – y + 1=0

Избавляемся от иррациональности в знаменателе

[b]((7 – sqrt(85))/6)*x – y + 1 = 0[/b]

[spoiler title=”источники:”]

http://4apple.org/sostavit-uravnenie-bissektris-uglov-obrazovannyh/

http://reshimvse.com/zadacha.php?id=34288

[/spoiler]

Пусть
имеем две прямые:

,
её
вектор нормали
=
и :

,
её
вектор нормали
=.
Будем предполагать, что векторы

и

всегда располагаются внутри одного из
углов, образуемых пересекающимися
прямыми (векторы

и
–
свободные!).
В общем случае прямые при пересечении
образуют один угол острый, а второй
тупой. Возникает классическая
задача:
найти уравнение биссектрисы тупого и
острого углов.

Существует
несколько способов решения задачи. В
каждом из них на первом шаге уста­навливается
факт: векторы

и

располага­ются в области тупого угла
или в области ост­рого. На этот вопрос
достаточно просто отве­чает скалярное
произведение векторов: а)
∙
> 0 – векторы расположены в области
тупого угла; б)
∙
< 0 – векторы расположены в области
острого угла. Далее рассмотрим наиболее
ин­тересные способы решения поставленной
задачи.

Способ–1.
Пусть векторы

и

располагаются в области тупого угла.
Учтём, что для точек, расположенных
внутри тупого угла с векторами

и

отклонения от прямых
и
положи­тельно: >0,
>0.
Это значит, что для точек биссектрисы
тупого угла выполняется равенство:

или: =. ()

Если бы
теперь нужно было построить биссектрису
острого угла, то уравнение нужно за­писать
в виде: =
–. ()

Если бы
векторы

и

располагались в области острого угла,
то биссектриса острого угла определялась
бы выражением ,
а биссектриса тупого –
выражением .

Способ–2.
В этом случае примем схему решения
задачи: а) находим точку

пересече­ния прямых
и ;
б) находим направление биссектрис ;
в) проводим прямую через заданную точку
в заданном направлении.

Для
определения направления биссектрис

построим единичные векторы:

и
,
затем суммы:
=+–определяет
направление биссектрисы угла, содержащего
векторы
,;

=––определяет
направление биссектрисы угла, смежного
первому.

Используя
угловой коэффициент вектора
,
строим биссектрису угла, содержащего
векторы
,;
если использовать угловой коэффициент
век­тора
,
построим биссектрису смежного угла.

Замечание: на
самом деле, достаточно найти толь­ко
один вектор:
для первой биссек­трисы он играет
роль направляющего вектора, а для второй
– роль вектора нормали.

Способ–3.
Воспользуемся уравнением пучка прямых:

и вектором
,
который будет иг­рать роль направляющего
или нормального, в зависимости от
конкретного задания.

Интересно рассмотреть
один и тот же пример, решив его сразу
всеми тремя способами: это позволит
сравнить их трудоёмкости!

☺☺

Пример
3–27:
Составить уравнение биссектрисы тупого
угла, образованного прямыми::;:.

Решение:

Имеем:

=(3,–4)
и
=(12,
5). Вычис­лим:
∙=>0
– векторы рас­по­ло­жены в области
тупого угла. Далее рас­смотрим решения
поставленной задачи тре­мя способами.

Способ–1.
Воспользуемся формулой

при условии равенства отклонений

произвольной точки
биссектрисы от
и :
=,
откуда получаем уравнение биссектрисы
выделенного угла: .

Способ–2.
В этом случае примем схему решения
задачи: а) находим точку
,
в которой пересекаются прямые
и ;
б) находим направление бис­сектрис
;
в) проводим прямую через заданную точку
в заданном направлении.

Координаты
точки
находим из системы урав­нений:
→

=.

Для
определения направления искомой
биссектрисы

построим единичные векторы
=(3,–4)
и
=(12,5),
затем вектор суммы:
=–=–(3,11)
– нормаль биссектрисы угла, содержащего
векторы
,.
Примем:
=(3,11).
Тогда уравнение биссек­трисы запишем
в виде: 3+11=0,
или .

Способ–3.
Воспользуемся уравнением пучка :

+=0,
или в виде:
=0
и направляющим вектором
=(11,–3).
Вектору

соответствует угловой коэффициент

=–.
Тогда:
===–.
Получаем уравнение искомой биссектрисы:
.

Ответ:
искомая
биссектриса: .

Замечание: трудоёмкость
рассмотренных способов различна;
одновременное использование разных
способов полезно наблюдением одинакового
окончательного результата.

☻

Соседние файлы в папке ЛА и АГ пособие

• #
• #
• #
• #
• #
• #

We will learn how to find
the equations of the bisectors of the angles between two straight lines.

Prove that the equation of the bisectors of the angles
between the lines a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0 are given by (frac{a_{1}x + b_{1}y +
c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = ±(frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2}
+ b_{2}^{2}}}).

Let us assume the two given straight lines be PQ and RS whose equations are a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0 respectively, where c(_{1}) and c(_{2}) are of the same symbols.

First we will find the equations of the bisectors of the angles between the lines a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0.

Now, let us
assume that the two straight lines PQ and RS intersect
at T and ∠PTR contains origin O.

Again, let us assume that TU is the bisector of ∠PTR and Z(h, k) is any point on TU. Then the origin O and the point Z are on the same side of both the lines PQ and RS.

Therefore, c(_{1}), and (a(_{1})h + b(_{1})k + c(_{1})) are of the same symbols and c(_{2}) and (a(_{2})h + b(_{2})k + c(_{2})) are also of the same symbols.

Since, we already assumed that c(_{1}), and c(_{2}), are of the same symbols, thus, (a(_{1})h + b(_{1})k + c(_{1})) and (a(_{2})h + b(_{2})k + c(_{2})) shall be of the same symbols.

Therefore, the lengths of the perpendiculars from Z upon PQ and RS are of the same symbols. Now, if ZA ⊥ PQ and ZB ⊥ RS then it implies that ZA = ZB.

⇒ (frac{a_{1}h + b_{1}k + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = (frac{a_{2}h + b_{2}k + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})

Therefore, the equation to the locus of Z (h, k) is,

(frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = (frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})………… (i), which is the equation of the bisector of the angle containing the origin.

Algorithm to find the bisector of the angle containing the origin:

Let the equations of the two lines be a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0.

To find the bisector of the angle containing the origin, we proceed as follows:

Step I: First check whether the constant terms c(_{1}) and c(_{2}) in the given equations of two straight lines are positive or not. Suppose not, then multiply both the sides of the equations by -1 to make the constant term positive.

Step II: Now obtain the bisector corresponding to the positive symbol i.e. 

(frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = + (frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}}), which is the required bisector of the angle containing the origin.

Note:

The bisector of the angle containing the origin means the
bisector of that angle between the two straight lines which contains the origin within it.

Again, ∠QTR does
not contain the origin. Suppose, TV be the bisector of ∠QTR and Z'(α, β) be any point on TV then the origin O and Z’ are on
the same side of the straight line (PQ) but they are on opposite sides
of the straight line RS.

Therefore, c(_{1}) and (a(_{1})α + b(_{1})β + c(_{1})) are of the same symbols but c(_{2}) and (a(_{2})α + b(_{2})β + c(_{2})), are of opposite symbols.

Since, we already assumed that, c(_{1}), and c(_{2}),
are of the same symbols, thus, (a(_{1})α + b(_{1})β + c(_{1})) and (a(_{2})α + b(_{2})β + c(_{2})) shall be of opposite symbols.

Therefore, the lengths of the perpendiculars from Z’ upon PQ and RS are of opposite symbols. Now, if Z’W ⊥ PQ and Z’C ⊥
RS then it readily follows that Z’W = -Z’C

⇒ (frac{a_{1}α +
b_{1}β + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = – (frac{a_{2}α + b_{2}β +
c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}}) 

Therefore, the equation to the locus of Z’ (α, β) is

(frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} +
b_{1}^{2}}}) = – (frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}}) ………… (ii), which is the
equation of the bisector of the angle not containing the origin.

From (i) and (ii) it is seen that the equations of the
bisectors of the angles between the lines a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0 are (frac{a_{1}x +
b_{1}y + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = ±(frac{a_{2}x + b_{2}y +
c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}}).

Note: The bisectors (i) and (ii) are perpendicular to each
other.

Algorithm to find the
bisectors of acute and obtuse angles between two lines:

Let the equations of the two lines be a(_{1})x + b(_{1})y + c(_{1}) = 0 and a(_{2})x + b(_{2})y + c(_{2}) = 0. To separate the bisectors of the obtuse and acute angles
between the lines we proceed as follows:

Step I: First check whether the constant terms c(_{1}) and c(_{2})
in the two equations are positive or not. Suppose not, then multiply both the sides
of the given equations by -1 to make the constant terms positive.

Step II: Determine the symbols of the expression a(_{1})a(_{2})
+ b(_{1})b(_{2}).

Step III: If a(_{1})a(_{2}) + b(_{1})b(_{2}) > 0,
then the bisector corresponding to “ + “ symbol gives the obtuse angle bisector
and the bisector corresponding to “ – “ is the bisector of the acute angle
between the lines i.e.

(frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} +
b_{1}^{2}}}) = + (frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})
and (frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = – (frac{a_{2}x
+ b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})

are the bisectors of obtuse and acute angles respectively.

If a(_{1})a(_{2}) + b(_{1})b(_{2}) < 0, then the
bisector corresponding to “ + “ and “ – “ symbol give the acute and obtuse
angle bisectors respectively i.e.

(frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} +
b_{1}^{2}}}) = + (frac{a_{2}x + b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})
and (frac{a_{1}x + b_{1}y + c_{1}}{sqrt{a_{1}^{2} + b_{1}^{2}}}) = – (frac{a_{2}x
+ b_{2}y + c_{2}}{sqrt{a_{2}^{2} + b_{2}^{2}}})

are the bisectors of acute and obtuse angles respectively.

Solved examples to find the equations of the bisectors of
the angles between two given straight lines:

1. Find the equations of the bisectors of the angles between
the straight lines 4x – 3y + 4 = 0 and 6x + 8y – 9 = 0.

Solution:

The equations of the bisectors of the angles between 4x – 3y
+ 4 = 0 and 6x + 8y – 9 = 0 are

(frac{4x – 3y + 4}{sqrt{4^2} + (-3)^{2}}) = ± (frac{6x
+ 8y – 9}{sqrt{6^2} + 8^{2}})

⇒ (frac{4x – 3y + 4}{5}) = ±(frac{6x + 8y – 9}{10})

⇒ 40x – 30y + 40 = ±(30x + 40y – 45)

Taking positive sign, we get,

⇒ 40x – 30y + 40 = +(30x + 40y – 45)

⇒ 2x – 14y + 17 = 0

Taking negative sign, we get,

⇒ 40x – 30y + 40 = -(30x + 40y – 45)

⇒ 40x – 30y + 40 = -30x – 40y + 45

⇒ 70x + 10y – 5 = 0

Therefore the equations of the bisectors of the angles
between the straight lines 4x – 3y + 4 = 0 and 6x + 8y – 9 = 0 are 2x – 14y +
17 = 0 and 70x + 10y – 5 = 0.

2. Find the equation of the obtuse angle bisector of lines 4x
– 3y + 10 = 0 and 8y – 6x – 5 = 0.

Solution:

First we make the constant terms positive in the given two
equations.

Making positive terms positive, the two equations becomes

4x – 3y + 10 = 0 and 6x – 8y + 5 = 0

Now, a(_{1})a(_{2}) + b(_{1})b(_{2}) = 4 × 6 + (-3) ×
(-8) = 24 + 24 = 48, which is positive. Hence, “+” symbol gives the obtuse
angle bisector. The obtuse angle bisector is

⇒ (frac{4x – 3y + 10}{sqrt{4^2} + (-3)^{2}}) = + (frac{6x
– 8y + 5}{sqrt{6^2} + (-8)^{2}})

⇒ (frac{4x – 3y + 10}{5}) = +(frac{6x – 8y + 5}{10})

⇒ 40x – 30y + 100 = 30x – 40y – 50

⇒ 10x + 10y + 150 = 0

x + y + 15 = 0, which is the required obtuse angle bisector.

● The Straight Line

• Straight Line
• Slope of a Straight Line
• Slope of a Line through Two Given Points
• Collinearity of Three Points
• Equation of a Line Parallel to x-axis
• Equation of a Line Parallel to y-axis
• Slope-intercept Form
• Point-slope Form
• Straight line in Two-point Form
• Straight Line in Intercept Form
• Straight Line in Normal Form
• General Form into Slope-intercept Form
• General Form into Intercept Form
• General Form into Normal Form
  
• Point of Intersection of Two Lines
  
• Concurrency of Three Lines
• Angle between Two Straight Lines
• Condition of Parallelism of Lines
• Equation of a Line Parallel to a Line
• Condition of Perpendicularity of Two Lines
• Equation of a Line Perpendicular to a Line
• Identical Straight Lines
• Position of a Point Relative to a Line
• Distance of a Point from a Straight Line
• Equations of the Bisectors of the Angles between Two Straight Lines
• Bisector of the Angle which Contains the Origin
• Straight Line Formulae
• Problems on Straight Lines
• Word Problems on Straight Lines
• Problems on Slope and Intercept

Составить уравнение биссектрис углов образованных двумя прямыми

Составить уравнение биссектрисы острого угла между прямыми

Решение

Найдем точку пересечения двух прямых

Направляющий вектор первой прямой есть , второй , так как их скалярное произведение положительно , поэтому найдем уравнение биссектрисы между векторами , проходящую через точку

Направляющий вектор биссектрисы угла равен сумме нормированных направляющих векторов сторон

Так как точка лежит на этой биссектрисе, то

Задание 8

Составить уравнение плоскости, которая проходит через точку параллельно плоскости

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9987 – | 7776 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.

Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0.

Расстояние от точки (x_o;y_o) до прямой ax+by+c=0 определяется по формуле

По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.

Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0, находится от этих прямых на одинаковом расстоянии, то есть

Это равенство можно записать в виде

Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.

Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.

В формулу уравнения биссектрис подставляем данные прямых:

Что ты хочешь узнать?

Ответ

Проверено экспертом

Даны прямые: 11x-2y+5=0 и 4x+8y-7=0

Уравнения биссектрис углов между прямыми Ax + By + C = 0 и A₁x + B₁y + C₁ = 0:

Знак + или – выбирается в зависимости от того, нужно уравнение биссектрисы острого или тупого углов.

Подставив коэффициенты заданных прямых в приведенную формулу, получим уравнения биссектрис:

В приближённом варианте у ≈ 1,3541х + 1,3772.

Уравнение биссектрисы угла

Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.

Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0.

Расстояние от точки (x_o;y_o) до прямой ax+by+c=0 определяется по формуле

По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.

Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0, находится от этих прямых на одинаковом расстоянии, то есть

Это равенство можно записать в виде

Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.

Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.

В формулу уравнения биссектрис подставляем данные прямых:

Уравнение биссектрисы в треугольнике — формула, свойства и решение задач

Прямая на плоскости

Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:

1. На плоскости, где достаточно двух координат для описания любых геометрических объектов.
2. В трехмерном пространстве, где любая точка имеет три координаты.

Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:

1. Общий. Он также называется универсальным. Прямая представляет собой следующую математическую запись: A*x + B*y + C = 0. Здесь A, B, C — числовые коэффициенты, x и y — переменные, являющиеся координатами. Сразу нужно отметить, что эта форма представления прямой используется для составления уравнения биссектрисы угла. Для удобства геометрического изображения общую форму записи часто представляют в виде y = f (x). Нужно понимать, что указанной форме в пространстве соответствует не прямая, а плоскость.
2. Канонический или уравнение в отрезках. Имеет оно такой вид: y/p + x/q = 1. Здесь p, q — это координаты, в которых прямая пересекает оси y и x, соответственно, поэтому удобно ее изображать в координатной системе.
3. Векторный. Это один из важных типов представления прямой как на плоскости, так и в пространстве. По сути, он является исходным представлением, из которого можно получить все остальные. Математически он записывается так: (x, y) = (x0, y0) + α*(v1, v2). Где (x0, y0) — координаты произвольной точки, которая лежит на прямой, (v1, v2) — направляющий вектор, он параллелен заданной прямой, α — произвольное число, параметр.
4. Параметрический. Этот тип представляет собой систему уравнений, которую удобно использовать во время преобразования одного вида прямой в другой. Представляет он собой следующую математическую запись: x = x0 + α*v1; y = y0 + α*v2. Несложно понять, что, выражая параметр α, можно получить уравнения общего вида и в отрезках. Объединяя же систему уравнений в одно выражение, получается векторная форма записи прямой.

Делящая пополам угол линия

Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.

Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.

Способы построения

В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:

1. С помощью транспортира. Для этого следует измерить заданный угол в градусах, разделить его пополам. Полученное значение отметить в виде точки. Затем соединить вершину угла и поставленную точку внутри него. Получится искомый элемент.
2. С использованием циркуля и линейки. Эти инструменты еще проще применять для построения биссектрисы, чем транспортир. Сначала необходимо установить в вершину угла ножку циркуля и отметить дугами пересечение окружности со сторонами. Затем, в точки пересечения поставить ножку циркуля и провести две окружности. Соединив две точки их пересечения одной прямой, можно получить биссектрису.

Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.

В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.

Основные свойства

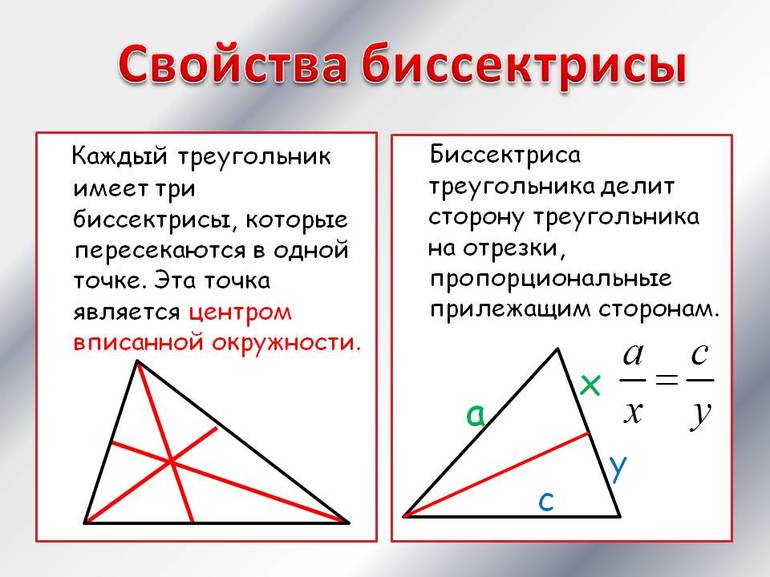
Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.

Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.

Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.

В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:

Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.

Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:

Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.

Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.

Уравнение биссектрисы треугольника

Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.

В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):

1. Сначала требуется определить уравнения двух сторон угла по их координатам. Это легко сделать в векторной форме, а затем, преобразовать ее в выражение общего типа.
2. Далее, необходимо найти уравнение биссектрис первого координатного угла, прировняв расстояния от ее точек до соответствующей стороны. Рабочая формула имеет вид: |A1*x + B1*y + C|/(A1 2 + B1 2 )^0,5 = |A2*x + B2*y + C|/(A2 2 + B2 2 )^0,5. Следует обратить внимание на наличие двух различных решений этого равенства, поскольку в числителе стоит модульное выражение. Два полученных уравнения говорят о наличии взаимно перпендикулярных биссектрис для углов треугольника внутреннего и внешнего.
3. Для внутреннего угла искомое уравнение можно найти, если определить точку пересечения соответствующей прямой с противоположной исходному углу стороной треугольника. Та точка, сумма расстояний от которой до концов отрезка будет равна длине стороны, принадлежит искомой биссектрисе.

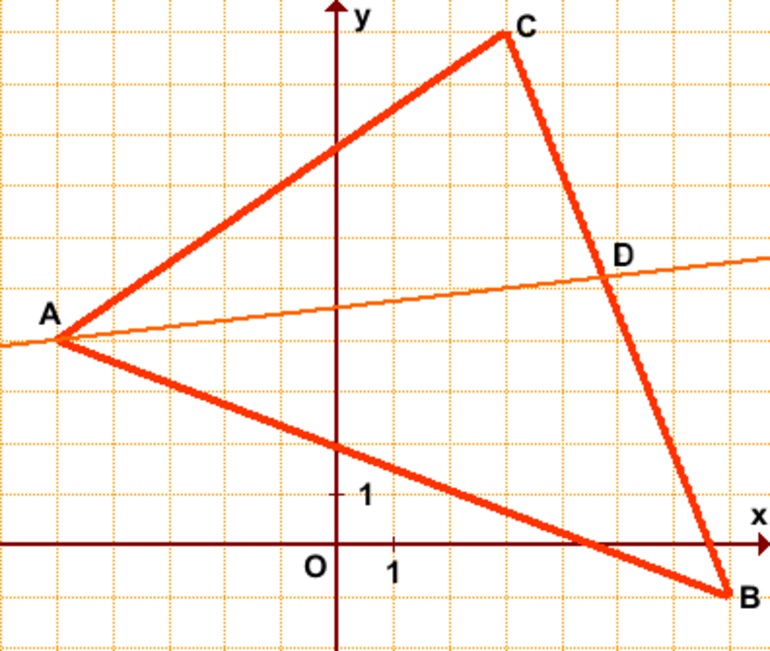
Пример решения задачи

Пусть, треугольник задан координатами A (1, -1), B (0, -2), C (3,0). Следует уравнение биссектрисы найти для угла B и ее длину вычислить.

Сначала нужно написать уравнения прямых для сторон AB и CB, получается:

• AB: (x, y) = (1, -1) + α*(-1, -1) ==> y — x + 2 = 0;
• CB: (x, y) = (3, 0) + α*(-3, -2) ==> 3*y — 2*x + 6 = 0.

Составить уравнения биссектрис можно так:

| y — x + 2 |/(2)^0,5 = | 3*y — 2*x + 6 |/(13)^0,5.

Решение этого уравнения приводит к следующим двум выражениям для взаимно перпендикулярных биссектрис:

• y*(6−3*3 0,5 ) + x*(3*3 0,5 −4)+12−6*3 0,5 = 0;
• y*(3*3 0,5 +6) -x*(4+3*3 0,5 )+12+6*3 0,5 = 0.

Чтобы определить, какая из двух прямых является искомой для треугольника заданного, следует точку пересечения каждой из них со стороной AC найти. Уравнение для AC имеет вид:

Подставляя его в каждое из выражений для биссектрис, можно получить две точки пересечения:

При этом длина основания AC составляет 2,236 единицы через единичный вектор. Расстояние от точек D1 и D2 до A, C равно:

• D1A = 1,4; D1C = 3,635;
• D2A = 0,621; D2C = 1,614.

Видно, что точка пересечения второй прямой D2 лежит между A и C, поэтому соответствующее ей уравнение биссектрисы является ответом на задачу. Ее длину можно вычислить по формуле для модуля вектора BD2:

BD2 = 2,014 единицы.

Таким образом, для определения в треугольнике биссектрисы уравнения по координатам следует уметь находить векторную форму выражений для прямой по координатам двух точек. Также нужно знать свойства делящей пополам угол линии.

Как найти уравнение биссектрисы

Пусть даны две пересекающиеся прямые, заданные своими уравнениями. Требуется найти уравнение прямой, которая, проходя через точку пересечения этих двух прямых, делила бы точно пополам угол между ними, то есть являлась бы биссектрисой.

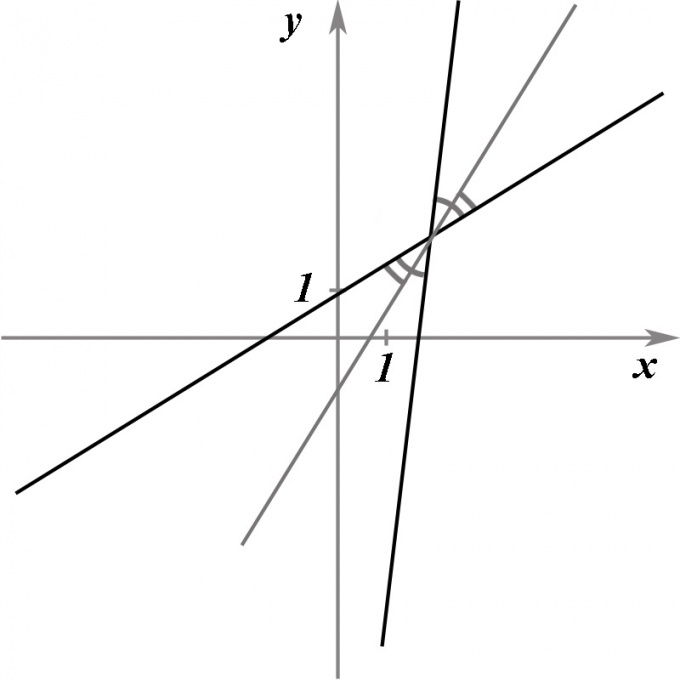
Инструкция

Предположим, что прямые заданы своими каноническими уравнениями. Тогда A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0. При этом A1/B1 ≠ A2/B2, иначе прямые параллельны и задача не имеет смысла.

Поскольку очевидно, что две пересекающиеся прямые образуют между собой четыре попарно равных угла, то должны существовать ровно две прямые, удовлетворяющие условию задачи.

Эти прямые будут перпендикулярны друг другу. Доказательство этого утверждения достаточно просто. Сумма четырех углов, образованных пересекающимися прямыми, будет всегда равна 360°. Поскольку углы попарно равны, то эту сумму можно представить в виде:
2a + 2b = 360° или, что очевидно, a + b = 180°.
Поскольку первая из искомых биссектрис делит пополам угол a, а вторая — угол b, то угол между самими биссектрисами всегда равен a/2 + b/2 = (a + b)/2 = 90°.

Биссектриса, по определению, делит угол между прямыми пополам, а значит, для любой точки, лежащей на ней, расстояния до обеих прямых будут одинаковыми.

Если прямая задана каноническим уравнением, то расстояние от нее до некоторой точки (x0, y0), не лежащей на этой прямой:
d = |(Ax0 + By0 + C)/(√(A^2 + B^2))|.
Следовательно, для любой точки, лежащей на искомой биссектрисе:
|(A1*x + B1*y + C1)/√(A1^2 + B1^2)| = |(A2*x + B2*y + C2)/√(A2^2 + B2^2)|.

Из-за того, что в обеих частях равенства стоят знаки модуля, оно описывает сразу обе искомые прямые. Чтобы превратить его в уравнение только одной из биссектрис, нужно раскрыть модуль либо со знаком +, либо со знаком -.
Таким образом, уравнение первой биссектрисы:
(A1*x + B1*y + C1)/√(A1^2 + B1^2) = (A2*x + B2*y + C2)/√(A2^2 + B2^2).
Уравнение второй биссектрисы:
(A1*x + B1*y + C1)/√(A1^2 + B1^2) = -(A2*x + B2*y + C2)/√(A2^2 + B2^2).

Например, пусть заданы прямые, определенные каноническими уравнениями:
2x + y -1 = 0,

x + 4y = 0.
Уравнение их первой биссектрисы получается из равенства:
(2x + y -1)/√(2^2 + 1^2) = (x + 4y + 0)/√(1^2 + 4^2), то есть
(2x + y – 1)/√5 = (x + 4y)/√15.
Раскрывая скобки и переводя уравнение в канонический вид:
(2*√3 – 1)*x + (√3 – 4)*y – √3 = 0.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?