Как найти биссектрису угла на клетчатой бумаге

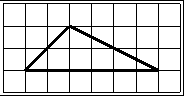
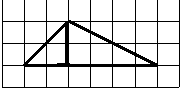
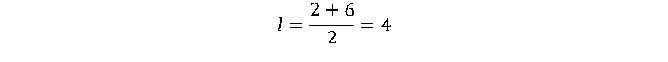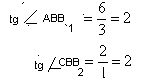Рассмотрим, каким образом может быть найдена биссектриса треугольника по рисунку на клетчатой бумаге.

Задача

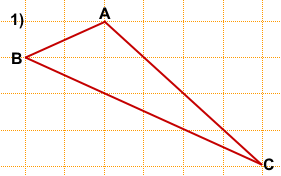
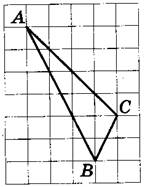
На клетчатой бумаге с размером клетки 1×1 изображен треугольник ABC.

Найдите длину его биссектрисы, проведённой из вершины B.

Решение:

1) Треугольник ABD — равнобедренный с основанием AD.

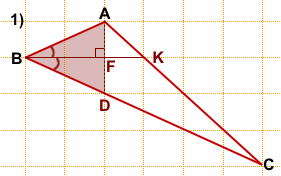
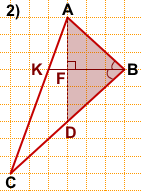
Отрезок BF, перпендикулярный основанию AD — высота, медиана и биссектриса треугольника ABD (по свойству равнобедренного треугольника).

Таким образом, ∠ABF=∠DBF.

Продолжим BF до пересечения со стороной AC. На пересечении BF и AC отметим точку K.

BK — биссектриса треугольника ABC, проведённая из вершины B.

Длину BK считаем по клеточкам. BF=3.

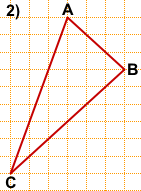
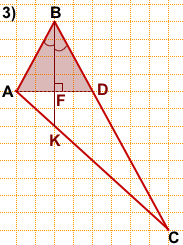
2) Треугольник ABD — равнобедренный с основанием AD.

AF — его высота, медиана и биссектриса.

Продлеваем AF до пересечения со стороной AC в точке K.

BK — искомая биссектриса треугольника ABC.

Длину BK находим по клеточкам: BK=4.

3) В равнобедренном треугольнике ABD

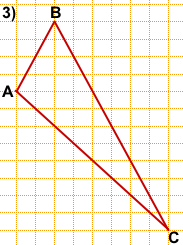
AF — высота, медиана и биссектриса.

Продолжим BF. На пересечении со стороной AC получим точку K.

BK — биссектриса треугольника ABC, длину которой нам нужно найти.

По клеточкам BK=6.

Задания

Версия для печати и копирования в MS Word

Задание 3. ЕГЭ. Найти длину биссектрисы треугольника

Задание. На клетчатой бумаге с размером клетки 1 × 1 изображен треугольник ∆АВС. Найдите длину его биссектрисы, проведенной из вершины В.

Решение:

Проведем DC, тогда треугольник ΔBCD — равнобедренный треугольник с основанием DС. Высота, проведенная из вершины В равнобедренного треугольника ΔBCD, является  биссектрисой этого треугольника.

Следовательно, ВК — биссектриса угла В и ВК — биссектриса треугольника ΔАВС. Получим ВК = 6.

Ответ: 6

Первым делом я вспомнил школьный курс, хотя было это сорок лет назад – десять классов я закончил в 1982-м году. И припомнилось мне одно весёлое определение, очень доступно объясняющее, что такое “биссектриса” на самом деле. говорили, что “биссектриса – это такая крыса, которая ходит по всем углам и делит их ровно пополам”.

Что касается конкретного вопроса, то в данном случае абсолютно случайно или преднамеренно задача поставлена так, что для её решения не требуется никаких компьютеров или даже калькуляторов.

Главное – правильно определить направление и хотя бы мысленно провести черту – отрезок, соединяющий вершину треугольника B и сторону AC. В данном случае это окажется банальная вертикаль, длина которой составит те самые три клетки, которые по условиям задания соответствуют трём сантиметрам.

Почему так? Всё довольно просто. Также мысленно проведите горизонталь от точки C до стороны треугольника AB. Пусть там будет точка D. Согласитесь, мы получим равнобедренный треугольник BCD? Так где же ещё проходить биссектрисе из угла B, если не на равном расстоянии между точками C и воображаемой D? Между ними всего две клеточки. Стало быть, черту следует проводить на удалении в одну клетку от B и C. Для движения в том же направлении остаётся всего навсего одна клетка, которая и добавляет длине третий сантиметр. В итоге мы имеем 3 сантиметра для длины биссектрисы треугольника из угла B.

Сам вопрос мне понравился именно тем, что он из серии “на сообразительность” и не требует применения правил высшей математики или начертательной геометрии.

---

Квадратная решетка и координатная плоскость

---

В задании №3 профильного уровня ЕГЭ по математике мы будем работать с фигурами на квадратных решетках – вычислять параметры фигур – стороны или площади, а также расстояния между точками. Приступим непосредственно к разбору типовых вариантов.

---

Разбор типовых вариантов заданий №3 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите площадь.

[/su_note]

Алгоритм решения:

1. Подсчитываем длину основания и высоты.
2. Записываем формулу вычисления площади.
3. Вычисляем площадь.
4. Записываем ответ.

Решение:

1. Подсчитываем длины основания и высоты:

основание = 6,

высота = 2.

2. Записываем формулу площади треугольника: S= ah|2.

3. Вычисляем площадь: S= 6∙2/2=6

Ответ: 6.

---

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

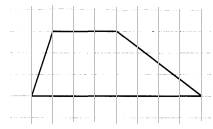
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

[/su_note]

Алгоритм решения:

1. Подсчитываем длину каждого основания и высоты трапеции.
2. Записываем формулу длины средней линии трапеции.
3. Вычисляем среднюю линию.
4. Записываем ответ.

Решение:

1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 3, большее – 4.

2. Длина средней линии трапеции находится по формуле

, где a и b – длина верхнего и нижнего оснований трапеции.

3. Имеем:

.

4. Значит, средняя линия равна 3,5.

Ответ: 3,5.

---

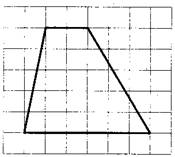
Третий вариант задания (из Ященко, №2)

[su_note note_color=”#defae6″]

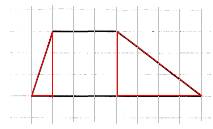
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

[/su_note]

Алгоритм решения:

1. Подсчитываем длину каждого основания и высоты трапеции.
2. Записываем формулу длины средней линии трапеции.
3. Вычисляем среднюю линию.
4. Записываем ответ.

Решение:

1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 2, большее – 6.

2. Длина средней линии трапеции находится по формуле

, где a и b – длина верхнего и нижнего оснований трапеции.

3. Имеем:

4. Значит, средняя линия равна 4.

Ответ: 4.

---

Четвертый вариант задания (из Ященко, №4)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины В.

[/su_note]

Алгоритм решения:

1. Проведем перпендикуряры из вершин Аи С.
2. Построим биссектрису угла В.
3. Покажем, что биссектриса параллельна высотам.
4. Измерим длину биссектрисы.
5. Запишем ответ.

Решение:

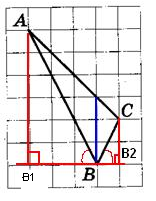
1. Проведем из вершин А и С отрезки АВ₁ иСВ₂, перпендикулярные прямой, содержащей вершину В на рисунке.

2. Построим биссектрису угла B.

3. Рассмотрим треугольники АВВ₁ иВВ₂С. Они прямоугольные, тогда из соотношений в прямоугольных треугольниках

Это означает, что углы АВB₁ и СВB₂ равны, так как равны тангенсы этих углов.

Раз равны углы, то стороны AB и BC расположены под одним углом относительно вертикали (На рисунке она проведена синим). Эта вертикаль является биссектрисой. Длина биссектрисы по рисунку равна 3.

Ответ: 3.

---

Пятый вариант задания (из Ященко, №7)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

[/su_note]

Алгоритм решения:

1. Рассмотрим рисунок и измерим основания.
2. Проведем высоту.
3. Запишем формулу площади трапеции.
4. Вычислим площадь по формуле.

Решение:

1. На рисунке основания равны 3 и 8.

2. Опустим высоту. Она рана 3.

3. Формула трапеции: S=h(a+b)/2, где a,b – основания, h – высота.

4. Вычислим площадь, подставив значения: S=3∙(3+8)/2=16,5

Следовательно, площадь данной трапеции равна 16,5.

Ответ: 16,5.

Даниил Романович | Просмотров: 12.3k