Как найти биссектрису в треугольнике 7 класс - Сайт, где вы сможете решить свои вопросы

Перпендикуляр от точки к прямой

Отрезок (AC) называется перпендикуляром, проведённым из точки (A) прямой (a), если прямые (AC) и (a) перпендикулярны.

Точка (C) называется основанием перпендикуляра.

От точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Докажем, что от точки (A), не лежащей на прямой (BC), можно провести перпендикуляр к этой прямой.

Допустим, что дан угол

∠ABC

Отложим от луча (BC) угол, равный данному, и совместим эти углы накладыванием (представим, что сложим лист бумаги с равными углами по стороне (BC)).

Сторона (BA) совместится со стороной

BA1

При этом точка (A) наложится на некоторую точку

Следовательно, совмещается угол

∠ACB

∠A1CB

Но углы

∠ACB

∠A1CB

— смежные, значит, каждый из них прямой.

Прямая

AA1

перпендикулярна прямой (BC), а отрезок (AC) является перпендикуляром от точки (A) к прямой (BC).

Если допустить, что через точку (A) можно провести ещё один перпендикуляр к прямой (BC), то он бы находился на прямой, пересекающейся с

AA1

. Но две к одной и той же прямой перпендикулярные прямые должны быть параллельны и не могут пересекаться.

Это противоречие, что означает: через данную точку к прямой можно провести только один перпендикуляр.

Медианы, биссектрисы и высоты треугольника

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Поэтому для построения медианы необходимо выполнить следующие действия:
1) найти середину стороны;
2) соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком — это и будет медиана.

У треугольника три стороны, следовательно, можно построить три медианы.

Все медианы пересекаются в одной точке.

Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.

Поэтому для построения биссектрисы необходимо выполнить следующие действия:
1) построить биссектрису какого-либо угла треугольника (биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части);
2) найти точку пересечения биссектрисы угла треугольника с противоположной стороной;
3) соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса треугольника.

У треугольника три угла и три биссектрисы.

Все биссектрисы пересекаются в одной точке.

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону.

Поэтому для построения высоты необходимо выполнить следующие действия:
1) провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);
2) из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к ней (перпендикуляр — это отрезок, проведённый из точки к прямой, составляющей с ней угол 90°) — это и будет высота.

Так же как медианы и биссектрисы, треугольник имеет три высоты.

Высоты треугольника пересекаются в одной точке.

Но, как выше упомянуто, для некоторых видов треугольников построение высот и точки их пересечения отличаются.

Если треугольник с прямым углом, то стороны, образующие прямой угол, можно назвать высотами, так как они перпендикулярны одна к другой. Точкой пересечения высот является общая вершина перпендикулярных сторон.

Если треугольник с тупым углом, то высоты, опущенные с вершин острых углов, выходят вне треугольника к продолжениям сторон. Прямые, на которых расположены высоты, пересекаются вне треугольника.

Обрати внимание!

Если из одной и той же вершины провести медиану, биссектрису и высоту, то медиана окажется самым длинным отрезком, а высота — самым коротким отрезком.

Равнобедренный треугольник

Если у треугольника две стороны равны, то такой треугольник называют равнобедренным.

Равные стороны называют боковыми, а третью сторону — основанием.

(AB = BC) — боковые стороны , (AC) — основание.

Если у треугольника все три стороны равны, то такой треугольник является равносторонним.

Равнобедренный треугольник имеет некоторые свойства, которые не имеют треугольники с разными сторонами.

1. В равнобедренном треугольнике углы при основании равны.

2. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

3. В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.

4. В равнобедренном треугольнике высота, проведённая к основанию, является биссектрисой и медианой.

Первое и второе свойство можно доказать, если докажем равенство двух треугольников, которые образуются, если из угла напротив основания провести биссектрису (BD).

Рассмотрим равнобедренный треугольник (ABC) с основанием (AC) и докажем, что

ΔABD=ΔCBD

Пусть (BD) — биссектриса треугольника (ABC).

ΔABD=ΔCBD

по первому признаку равенства треугольников ((AB = BC) по условию, (BD) — общая сторона,

∠ABD=∠CBD

, так как (BD) — биссектриса).

У равных треугольников равны все соответствующие элементы:

∠A=∠C

— доказано, что прилежащие основанию углы равны.

2. (AD = DC) — доказано, что биссектриса является медианой.

∠ADB=∠CDB

— так как смежные углы, сумма которых

180°

, равны, то каждый из них равен

90°

, то есть медиана является высотой.

Можно очень легко самостоятельно доказать и третье, и четвёртое свойства.

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Треугольники
Биссектрисы треугольника

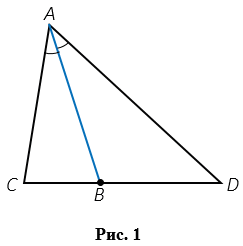
Биссектриса треугольника – это отрезок биссектрисы угла, который соединяет вершину треугольника с точкой противоположной стороны. На Рис.1 АВ – биссектриса треугольника АСD (соединяет вершину А с точкой В, лежащей на стороне СD).

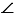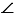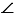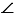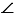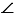Любой треугольник имеет три биссектрисы. На Рис.2, АВ, СК, DМ – биссектрисы треугольника АСD. Биссектриса АВ соединяет вершину А с точкой В, лежащей на стороне СD ( САВ = ВАD); биссектриса СК соединяет вершину С с точкой К, лежащей на стороне AD ( АСК = КСD); биссектриса DM соединяет вершину D с точкой M, лежащей на стороне AC ( СDM = MDA).

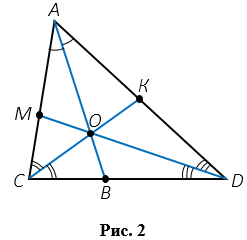
Замечательное свойство биссектрис треугольника: в любом треугольнике биссектрисы пересекаются в одной точке. На Рис.2 биссектрисы треугольника АDС пересекаются в точке О.

Советуем посмотреть:

Треугольник

Равенство треугольников

Первый признак равенства треугольников

Перпендикуляр к прямой

Медианы треугольника

Высоты треугольника

Равнобедренный треугольник

Свойства равнобедренного треугольника

Второй признак равенства треугольников

Третий признак равенства треугольников

Окружность

Построения циркулем и линейкой

Треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 230,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 272,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 275,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 317,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 334,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 535,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 537,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 852,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 872,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 900,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Определение биссектрисы угла треугольника
Свойства биссектрисы треугольника
- Свойство 1 (теорема о биссектрисе)
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
Пример задачи

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

BD – биссектриса угла ABC;
α = β.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

СD – внешняя биссектриса угла, смежного с ∠ACB;
α = β.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD² = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

CD – внутренняя биссектриса ∠ACB;
CE – биссектриса угла, смежного с ∠ACB;
∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC² = AB² + AC² = 6² + 8² = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD² = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Следовательно, AD ≈ 4,85 см.

Источник

Геометрия

7 класс

Урок № 12

Медианы треугольника. Биссектрисы треугольника. Высоты треугольника

Перечень рассматриваемых вопросов:

Понятие медианы, биссектрисы, высоты треугольника.
Построение медианы, высоты, биссектрисы.
Точки пересечения медианы, высоты и биссектрисы в треугольнике.
Создание представления о замечательных точках в треугольнике.

Тезаурус:

Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.

Биссектриса угла треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Основная литература:

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Дополнительная литература:

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Вы уже знакомы с такими понятиями как треугольник, угол, биссектриса угла.

Разберем, как построить биссектрису треугольника, а также узнаем, что такое медиана и высота треугольника.

Начнём с понятия биссектриса угла треугольника. Это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. AF – биссектриса ∠A треугольника ABC.

AA₁, BB₁, CC₁ _– биссектрисы ∆АВС

В любом треугольнике биссектрисы пересекаются в одной точке.

Введём понятие медианы треугольника.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

BM – медиана треугольника ABC.

AA₁, BB₁, CC₁– медианы ∆АВС.

В любом треугольнике медианы пересекаются в одной точке.

Введём понятие высоты треугольника.

Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

AH – высота треугольника ABC.

AH₁, BH_2, CH₃– высоты ∆АВС.

В любом треугольнике высоты или их продолжения пересекаются в одной точке.

Итак, сегодня мы узнали, какие отрезки называются медианой, биссектрисой, высотой треугольника, и научились их изображать с помощью чертёжных инструментов.

Рассмотрим, как можно решить задачу на доказательство, используя понятие «медиана треугольника».

На рисунке изображён треугольник ABC, при этом AD – медиана ∆ABC продолжена за сторону BC, так что AD = DE.

Докажем, что треугольники ABD и CED равны.

Дано:

АD – медиана ∆ABC.

AD = DE.

Доказать:

∆ABD = ∆CED.

Доказательство:

По условию в треугольниках ABD и CED: сторона AD равна стороне DE. Т. к. АD – медиана ∆ABC, то, по определению медианы, BD = DC.

∠ADB = ∠CDE (по свойству вертикальных углов).

Следовательно, ∆ABD = ∆CED (по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны).

Что и требовалось доказать.

Разбор решения заданий тренировочного модуля.

Задача 1.

В треугольнике ABC проведены биссектрисы AD и BM, которые пересекаются в точке O. Найдите углы треугольника ABO, если ∠BAC = 50°, ∠ABC = 80°, а сумма углов треугольника ABO равна 180°.