Ученик
(68),
закрыт
12 лет назад
KazeZlat
Профи
(849)
12 лет назад
2^3 бит = 1 байт
2^13 бит = 2^10 байт = 1 килобайт
2^23 бит = 2^20 байт = 2^10 килобайт = 1 мегабайт
2^33 бит = 2^30 байт = 2^20 килобайт = 2^10 мегабайт = 1 гигабайт
2^43 бит = 2^40 байт = 2^30 килобайт = 2^20 мегабайт = 2^10 гигабайт = 1 терабайт
и так далее.
двойка – основное значение в компьютере, т. к. его алфавит состоит из 2 значений (0 и 1)
т. е. если у тя 8 бит, то это 1 байт, а если у тебя 50331648 бит то это 6*(2^23) бит, а это 6 мегабайт.
|
Информатика. Какую можно сделать наглядную таблицу для перевода одной единицы измерения информации в другую (бит, байт, килобайт, мегабайт, гигабайт, терабайт, петабайт)? Для измерения объема информации существуют специальные единицы измерения – байты, биты. Бит – минимальная единица измерения информации. При двоичной системе счисления бит соответствует 1 двоичной цифре. Байт состоит из 8 бит. Для запоминания и перевода байтов в биты, гигабайты, мегабайты можно пользоваться таблицами. Они представлены ниже. система выбрала этот ответ лучшим Ксарфакс 3 года назад Самыми маленькими единицами измерения количества информации являются биты и байты. Думаю, все помнят, что в 1 байте содержится 8 бит. Килобайты, мегабайты, гигабайты и т.д. – это единицы, являющееся производными от байта. Они образуются с помощью специальных приставок (“кило”, “мега”, “гига” и т.д.), и каждая последующая единица равна произведению предыдущей на 2 в степени 10. То есть в 1 килобайте будет 2^10 = 1024 байта, в 1 мегабайте будет 2^10 = 1024 килобайта и т.д. Таблицу битов, байтов, килобайтов, мегабайтов, гигабайтов, терабайтов, петабайтов можно составить такую: Допустим, как посмотреть в этой таблице соотношение гигабайта с другими единицами измерения информации? Находим столбец с заголовком “1 Гигабайт”, а затем берём строку с нужной единицей. На их пересечении будет соответствующая цифра. То есть 1 Гигабайт – это 2^30 байтов, 2^20 килобайтов, 2^10 мегабайтов. ** Стоит отметить, что биты обычно соотносят не с производными байта, а с производныими бита – килобиты, мегабиты, гигабиты и т.д. Но смысл здесь тот же самый: килобит – это 2^10 бит, мегабит – это 2^20 бит и т.д. Также приведу схему, где наглядно отображено, как переводить из одних единиц измерения информации в другие. Возьмём для примера мегабайты. 1 мегабайт > 1 килобайта, поэтому для перевода мегабайтов в килобайты нужно количество мегабайт умножить на 2^10 (или 1024). Например, 10 мегабайт – это 10 * 1024 = 10240 килобайта. 1 мегабайт < 1 гигабайта, поэтому для перевода мегабайтов в гигабайты нужно количество мегабайт разделись на 2^10 (или 1024). Например, 100 мегабайт – это 100 / 1024 = 0,098 гигабайт. Nastya Chuk 3 года назад Итак, для измерения длины есть различные единицы : миллиметр, сантиметр, метр и т.п.Наш же компьютер работает непосредственно с самой информацией и как раз таки для измерения ее объема также имеются соответствующие единицы измерения : байты, килобайты, мегабайты и так далее.Соотношение этих единиц измерения приведены в таблице ниже. Цепочка имеет закономерную последовательность и оборачиваемость, что позволяет более структурировано запомнить школьнику или студенту в своей голове.Минимальной единицей в нашей табличке – это бит, а наибольшая – это эксабайт.Я полагаю, что это не все единицы измерения, но здесь приведены самые часто используемые в информатике. smile6008 3 года назад Составить таблицу соотношения величин не сложно, для этого нужно понимать, что 1 байт равен 8 битам и так далее. Каждая следующая еденица будет равно десятой степени предыдущей. Составим таблицу. В столбик слева напишем все необходимое нам показатели :байт, бит, килобайт, мегабайт, гигобайт, терабайт и петабайт. В верхней строке, начиная со второй, напишем все указанные ранее показатели, только добавим еденицу измерения один. Получим 1 бит, 1 байт и т. д. Пересечение этих значений в таблице и будет ответом на вопрос. Например, 1 килобайт равен 2 битам в тринадцатой степени или 2 еденицам байтов в десятой степени. При знании мер и сколько они составляют по отношению друг к другу вы сможете составить таблицу соотношения мер измерения информации. Мой колега указывал таблицу выше и я с ней соглашаюсь: Здесь действительно есть условное обозначение единиц информации, являющихся основными и используются в информатике. Это – таблица инженерного характера: Алиса в Стране 3 года назад Хорошо иметь такую таблицу перед глазами (кому часто нужна информация из этой таблицы) или под рукой, чтобы легко и быстро можно было ее найти, потому что вот я, например, постоянно в них путаюсь, ну не запоминаются они у меня, хотя вот математику то я люблю, но это несколько другое все же. Мне сложно даже запомнить что в 1 байте 8 битов. А дальше уже по возрастанию идут килобайты, мегабайты, гигабайты и т.д., и ладно бы еще там разница между ними была в 1000 раз, но ведь нет же, система то счисления там другая, двоичная, поэтому: 1 килобайт = 2 в 10 степени байтов 1 мегабайт = 2 в 10 степени килобайтов и т.д. Вот вроде все понятно, но не могу запомнить. Поэтому картинка вот для таких же как я: А если нужна именно таблица, то вот для байтов: Для битов: Марина Вологда 3 года назад Проще всего сделать именно в виде таблицы.Составляем таблицу в виде 10 строк и 7 столбиков. Но вы можете сами определить, что будете вносить в таблицу, а что нет. Вы на свое усмотрение можете изменять таблицу, только основные данные должны быть внесены. В первом столбце писать исходную единицу, а дальше на увеличение, тогда будет все понятно. Сначала пишем бит, затем байт. Указываем, что 1 байт равен 8 битам. Визуально таблица может выглядеть вот так: Если вы не умеете делать таблицы, можно записать в строчку. Первым опять пишем бит. Можно представить в виде вот такой таблицы, здесь она больше выглядит как схема, но все наглядно видно, когда надо делить, а когда умножать: Лара Изюминка 3 года назад Все достаточно просто. Во-первых заучить, что 1 байт = 8 бит Далее рассказывается, что так как в информатике принята не десятичная а двоичная система счисления, то приставка кило у нас означает не тысяча, а 1024, так как это 2 в 10 степени, число максимально близкое к 1000. 1кбайт=1024байт=1024*8бит 1мбайт=1024кбайт=1024*1024байт 1гбайт=1024мбайт=1024*1024*1024байт 1тбайт=1024гбайт=1024*1024*1024*1024байт Дальше обычно в школьном курсе не изучается, но для особо одаренных сообщается, что есть и петабайт и эксабайт и зеттабайт и йоттабайт, причем каждая последующая единица отличается от предыдущей в 1024 раза или 2 в 10 степени. Задание по предмету Информатика, составить таблицу соотношения мер измерения информации, делается просто если вы знаете эти меры и сколько они составляют по отношению друг к другу. Можно сделать вот такую простенькую таблицу и этого будет достаточно – В этой таблице имеется условное обозначение основных единиц информации, используемых в рамках информатики средней школы, и их отношение друг к другу. А вот таблица ниже носит более информативный характер, можно сказать “инженерный” и пятерка с плюсом за это задание вам обеспечена. Но и при ее нанесении (расчерчивании) и заполнении тоже придется потрудиться. 127771 более года назад Стоит сказать, что бит это наименьшая единица измерения. Мне удалось найти отличную таблицу, посмотрев которую, станет все понятно: Чтобы в этом разобраться, нужно знать, что один байт равен восемь битов. Один килобайт равен 1024 байтов. Стоит также также различать байты и биты. Один килобит равен 2^10 битов. Ниже представлена таблица для битов: Ниже представлена таблица для байтов: Знаете ответ? |
Как найти биты в информатике
Содержание
- Алфавитный подход к определению количества информации
- РЕШЕНИЕ ЗАДАЧ
- Информация.
- Теория:
- Теория:
- Теория:
- Теория:
- Заполняем пробелы – расширяем горизонты!
- Таблица байтов:
- Продолжение следует…
Алфавитный подход к определению количества информации
РЕШЕНИЕ ЗАДАЧ
При хранении и передаче информации с помощью технических устройств информацию следует рассматривать как последовательность символов — знаков (букв, цифр, кодов цветов точек изображения и т.д.).
| N=2 i | i | Информационный вес символа, бит |
| N | Мощность алфавита | |
| I=K*i | K | Количество символов в тексте |
| I | Информационный объем текста |
Возможны следующие сочетания известных (Дано) и искомых (Найти) величин:
| Тип | Дано | Найти | Формула |
|---|---|---|---|
| 1 | i | N | N=2 i |
| 2 | N | i | |
| 3 | i,K | I | I=K*i |
| 4 | i,I | K | |
| 5 | I, K | i | |
| 6 | N, K | I | Обе формулы |
| 7 | N, I | K | |
| 8 | I, K | N |
Задача 1. Получено сообщение, информационный объем которого равен 32 битам. чему равен этот объем в байтах?
Решение: В одном байте 8 бит. 32:8=4
Ответ: 4 байта.
Задача 2. Объем информацинного сообщения 12582912 битов выразить в килобайтах и мегабайтах.
Решение: Поскольку 1Кбайт=1024 байт=1024*8 бит, то 12582912:(1024*8)=1536 Кбайт и
поскольку 1Мбайт=1024 Кбайт, то 1536:1024=1,5 Мбайт
Ответ:1536Кбайт и 1,5Мбайт.
Задача 3. Компьютер имеет оперативную память 512 Мб. Количество соответствующих этой величине бит больше:
1) 10 000 000 000бит 2) 8 000 000 000бит 3) 6 000 000 000бит 4) 4 000 000 000бит Решение: 512*1024*1024*8 бит=4294967296 бит.
Ответ: 4.
Задача 4. Определить количество битов в двух мегабайтах, используя для чисел только степени 2.
Решение: Поскольку 1байт=8битам=2 3 битам, а 1Мбайт=2 10 Кбайт=2 20 байт=2 23 бит. Отсюда, 2Мбайт=2 24 бит.
Ответ: 2 24 бит.
Задача 5. Сколько мегабайт информации содержит сообщение объемом 2 23 бит?
Решение: Поскольку 1байт=8битам=2 3 битам, то
2 23 бит=2 23 *2 23 *2 3 бит=2 10 2 10 байт=2 10 Кбайт=1Мбайт.
Ответ: 1Мбайт
Задача 6. Один символ алфавита “весит” 4 бита. Сколько символов в этом алфавите?
Решение:
Дано:
| i=4 | По формуле N=2 i находим N=2 4 , N=16 |
| Найти: N — ? |
Ответ: 16
Задача 7. Каждый символ алфавита записан с помощью 8 цифр двоичного кода. Сколько символов в этом алфавите?
Решение:
Дано:
| i=8 | По формуле N=2 i находим N=2 8 , N=256 |
| Найти:N — ? |
Ответ: 256
Задача 8. Алфавит русского языка иногда оценивают в 32 буквы. Каков информационный вес одной буквы такого сокращенного русского алфавита?
Решение:
Дано:
| N=32 | По формуле N=2 i находим 32=2 i , 2 5 =2 i ,i=5 |
| Найти: i— ? |
Ответ: 5
Задача 9. Алфавит состоит из 100 символов. Какое количество информации несет один символ этого алфавита?
Решение:
Дано:
| N=100 | По формуле N=2 i находим 32=2 i , 2 5 =2 i ,i=5 |
| Найти: i— ? |
Ответ: 5
Задача 10. У племени “чичевоков” в алфавите 24 буквы и 8 цифр. Знаков препинания и арифметических знаков нет. Какое минимальное количество двоичных разрядов им необходимо для кодирования всех символов? Учтите, что слова надо отделять друг от друга!
Решение:
Дано:
| N=24+8=32 | По формуле N=2 i находим 32=2 i , 2 5 =2 i ,i=5 |
| Найти: i— ? |
Ответ: 5
Задача 11. Книга, набранная с помощью компьютера, содержит 150 страниц. На каждой странице — 40 строк, в каждой строке — 60 символов. Каков объем информации в книге? Ответ дайте в килобайтах и мегабайтах
Решение:
Дано:
| K=360000 | Определим количество символов в книге 150*40*60=360000. Один символ занимает один байт. По формуле I=K*iнаходим I=360000байт 360000:1024=351Кбайт=0,4Мбайт |
| Найти: I— ? |
Ответ: 351Кбайт или 0,4Мбайт
Задача 12. Информационный объем текста книги, набранной на компьютере с использованием кодировки Unicode, — 128 килобайт. Определить количество символов в тексте книги.
Решение:
Дано:
| I=128Кбайт,i=2байт | В кодировке Unicode один символ занимает 2 байта. Из формулыI=K*i выразимK=I/i,K=128*1024:2=65536 |
| Найти: K— ? |
Ответ: 65536
Задача 13.Информационное сообщение объемом 1,5 Кб содержит 3072 символа. Определить информационный вес одного символа использованного алфавита
Решение:
Дано:
| I=1,5Кбайт,K=3072 | Из формулы I=K*i выразимi=I/K,i=1,5*1024*8:3072=4 |
| Найти: i— ? |
Ответ: 4
Задача 14.Сообщение, записанное буквами из 64-символьного алфавита, содержит 20 символов. Какой объем информации оно несет?
Решение:
Дано:
| N=64, K=20 | По формуле N=2 i находим 64=2 i , 2 6 =2 i ,i=6. По формуле I=K*i I=20*6=120 |
| Найти: I— ? |
Ответ: 120бит
Задача 15. Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если его объем составил 1/16 часть мегабайта?
Решение:
Дано:
| N=16, I=1/16 Мбайт | По формуле N=2 i находим 16=2 i , 2 4 =2 i ,i=4. Из формулы I=K*i выразим K=I/i, K=(1/16)*1024*1024*8/4=131072 |
| Найти: K— ? |
Ответ: 131072
Задача 16. Объем сообщения, содержащего 2048 символов,составил 1/512 часть мегабайта. Каков размер алфавита, с помощью которого записано сообщение?
Решение:
Дано:
Примеры решения задач по информатике
Информация.
Теория:
1 Кб = 1024 байта
Переведите 2 Мб в Кб, байты, биты.
2 Мб * 1024 Кб = 2048 Кб
2 Мб * 1024 Кб * 1024 байт = 2097152 байт
2 Мб * 1024 Кб * 1024 байт * 8 бит = бит
2 Мб * 1024 Кб = 2048 Кб
2048 Кб * 1024 байт = 2097152 байт
2097152 байт * 8 бит = бит
Переведите бит в Мб, Кб, байты
бит : 8 бит = 3407872 байта
бит : 8 бит : 1024 байта = 3328 Кб
бит : 8 бит : 1024 байта : 1024 Кб = 3,25 Мб
бит :8 бит = 3407872 байта
3407872 байта : 1024 байта = 3328 Кб
3328 Кб : 1024 Кб = 3,25 Мб
Теория:
По умолчанию (если в задаче не указано специально) при решении задачи указывается 256-символьный алфавит – таблица ASCII (мощность алфавита = 256 символов). Значит, на один символ (букву, цифру, знак, знак препинания, пробел) приходится 8 бит информации или 1 байт.
Определить количество информации, которое содержится на печатном листе бумаги (двусторонняя печать), если на одной стороне умещается 40 строк по 67 символов в строке.
Определим количество символов на одной стороне листа:
40 строк * 67 символов = 2680 символов
Определим количество символов на 2-х сторонах листа:
2680 символов * 2 = 5360 символов
Количество информации = 5360 символов * 1 байт = 5360 байт
Переводим в Кб: 5360 байт : 1024 байт = 5,23 Кб
Если бы необходимо было получить ответ в бит, то
Количество информации = 5360 символов * 8 бит = 42880 бит
Переводим в байты 42880 бит : 8 бит = 5360 байт
Переводим в Кб 5360 байт : 1024 байт = 5,23 Кб
Теория:

где i – количество информации в бит, N – количество символов, количество событий
Символом является и знак препинания, и цифра, и специальные знаки. И пробел!
Какое количество информации будет содержаться на странице печатного текста при использовании 32-х символьного алфавита (на странице 60 строк по 56 символов).
Количество символов на странице = 60 строк * 56 символов = 3360 символов
По условию используется 32-х символьный алфавит (т. е. мощность алфавита = 32 символа).
Тогда 
Количество информации, содержащееся на странице = 3360 символов * 5 бит = 16800 бит
Переводим в байты: 16800 бит : 8 бит = 2100 байт
Переводим в Кб 2100 байт : 1024 байт = 2,05 Кб
общее количество символов на одной странице
количество бит информации, приходящейся на один символ
I
(количество информации)
Единицы измерения информации правой и левой части должны быть одинаковыми.
Какое количество символов содержится на странице энциклопедического словаря, если в памяти компьютера эта страница занимает 13 Кб?
По умолчанию количество бит информации, приходящейся на один символ, равно 8 бит.
Переведем 13 Кб в биты:
13 Кб * 1024 байт * 8 бит = 106496 бит
Используя данные предыдущей задачи и зная, что в одной строке находится 85 знаков, определить количество строк на странице.
Общее число символов на странице (по предыдущей задаче) = 13312 символов
Общее число символов 13312 символов
Количество символов в одной строке 85 знаков
Сколько бит содержится в слове ИНФОРМАЦИЯ?
Т. к. по умолчанию количество бит информации, приходящейся на 1 символ = 8 бит
(256-символьный алфавит, 
10 букв * 8 бит = 80 бит = 10 байт
В каком алфавите одна буква несет в себе больше информации, в русском или латинском? Примечание: в русском языке 33 буквы, в латинском – 26 букв.
Русский язык: 

Латинский язык: 
Количество бит информации одного символа русского языка больше на 1, чем в латинском языке.
Теория:
При форматировании дискеты 3.5 (А) ее физический размер составляет 1.44 Мб. Тем не менее, доступно для записи непосредственно самой информации пользователя только 1.37 Мб, т. к. 71,7 Кб отводится на создание каталога диска и нулевую дорожку.
Сколько дискет объемом 1.37 Мб необходимо для сохранения информации с винчестера объемом 40 Гб? А сколько CD-дисков?
Переводим единицы измерения информации к одному виду.
40 Гб * 1024 Мб = 40960 Мб
Количество дискет = 40960 Мб : 1.37 Мб =дискет.
Т. е. примерно 30 тыс. дискет 3.5 (А)!
Один CD-диск содержит примерно 700 Mb информации, тогда 40960 Mb / 700Mb = 58,51? Т. е. примерно 59 компакт-дисков CD-R объемом по 700 Мб.
Допустим, в вашем классе 27 человек.

Точной степени для этого уравнения нет (

В первом случае мы угадаем только из 16 человек, во втором из 32-х.
Значит, чтобы угадать из 27 человек необходимо получить 5 бит информации,
т. е. задать 5 вопросов.
Сколько символов содержится в алфавите, при помощи которого написана книга из 20 страниц, на каждой из которых содержится 15 строк по 20 символов и занимает в памяти компьютера вся книга 5,86 Кб.
Количество символов на одной странице — 15 строк * 20 символов = 300 символов
Всего символов в книге n = 300 символов * 20 страниц = 6000 символов
Общее количество информации I = бит в 1 символе * n символов
5,86 Кб = 48005,12 бит
Определим сколько бит в 1 символе:
x =


N=256 символов в алфавите
В алфавите некоторого формального языка всего два знака буквы. Каждое слово этого языка состоит обязательно из 7 букв. Какое максимальное число слов возможно записать в этом языке?
Т. к. для записи слов используется только 2 знака-буквы, при N-перемещениях существует

Решить уравнение 
Приведем выражение к общему основанию и общим единицам измерения.

x =
Какое количество информации несет в себе экран SVGA – монитора (16-bit кодирование, размер экрана 800*600)?
Определим, сколько всего пиксел содержится на всем экране:
* 16 бит = 7 бит = байт = 937,5 Кб = 0,9 Мб
Сколько цветов содержит рисунок размером 100*150 пиксел и объемом 29,3 Кб
Количество точек по вертикали
I
(количество информации)
Глубина цвета в бит
Количество точек по горизонтали
Количество цветов =
Тогда, 29,3 Кб = 30003,2 байт = 6 бит
Общее число точек = 100*150 =
Глубина цвета =
Тогда количество цветов =
256-цветный рисунок содержит 120 байт информации. Из скольких точек он состоит?
Т. к. рисунок содержит 256 цветов, то 
I = кол-во точек * глубину цвета
Количество точек = 
Достаточно ли видеопамяти объемом 256 Кб для работы монитора в режиме 640*480 точек и палитрой в 16 цветов.
Т. к. используется 16 цветов, значит глубина цвета = 4 бита (
640*480 = всего точек
Необходимое количество видеопамяти:
2 бит дано изначально
* 4 бита = 1 занимает экран

Заполняем пробелы – расширяем горизонты!
-
CompGramotnost.ru » Кодирование информации » Единицы измерения объема информации
Для измерения длины есть такие единицы, как миллиметр, сантиметр, метр, километр. Известно, что масса измеряется в граммах, килограммах, центнерах и тоннах. Бег времени выражается в секундах, минутах, часах, днях, месяцах, годах, веках. Компьютер работает с информацией и для измерения ее объема также имеются соответствующие единицы измерения.
Мы уже знаем, что компьютер воспринимает всю информацию через нули и единички.
Бит – это минимальная единица измерения информации, соответствующая одной двоичной цифре («0» или «1»).
Байт состоит из восьми бит. Используя один байт, можно закодировать один символ из 256 возможных (256 = 2 8 ). Таким образом, один байт равен одному символу, то есть 8 битам:
1 символ = 8 битам = 1 байту.
Буква, цифра, знак препинания – это символы. Одна буква – один символ. Одна цифра – тоже один символ. Один знак препинания (либо точка, либо запятая, либо вопросительный знак и т.п.) – снова один символ. Один пробел также является одним символом.
Изучение компьютерной грамотности предполагает рассмотрение и других, более крупных единиц измерения информации.
Таблица байтов:
1 Кб (1 Килобайт) = 2 10 байт = 2*2*2*2*2*2*2*2*2*2 байт =
= 1024 байт (примерно 1 тысяча байт – 10 3 байт)
1 Мб (1 Мегабайт) = 2 20 байт = 1024 килобайт (примерно 1 миллион байт – 10 6 байт)
1 Гб (1 Гигабайт) = 2 30 байт = 1024 мегабайт (примерно 1 миллиард байт – 10 9 байт)
1 Тб (1 Терабайт) = 2 40 байт = 1024 гигабайт (примерно 10 12 байт). Терабайт иногда называют тонна.
1 Пб (1 Петабайт) = 2 50 байт = 1024 терабайт (примерно 10 15 байт).
1 Эксабайт = 2 60 байт = 1024 петабайт (примерно 10 18 байт).
1 Зеттабайт = 2 70 байт = 1024 эксабайт (примерно 10 21 байт).
1 Йоттабайт = 2 80 байт = 1024 зеттабайт (примерно 10 24 байт).
В приведенной выше таблице степени двойки (2 10 , 2 20 , 2 30 и т.д.) являются точными значениями килобайт, мегабайт, гигабайт. А вот степени числа 10 (точнее, 10 3 , 10 6 , 10 9 и т.п.) будут уже приблизительными значениями, округленными в сторону уменьшения. Таким образом, 2 10 = 1024 байта представляет точное значение килобайта, а 10 3 = 1000 байт является приблизительным значением килобайта.
Такое приближение (или округление) вполне допустимо и является общепринятым.
Ниже приводится таблица байтов с английскими сокращениями (в левой колонке):
10 3 b = 10*10*10 b= 1000 b – килобайт
10 6 b = 10*10*10*10*10*10 b = 1 000 000 b – мегабайт
10 9 b – гигабайт
10 12 b – терабайт
10 15 b – петабайт
10 18 b – эксабайт
10 21 b – зеттабайт
10 24 b – йоттабайт
Выше в правой колонке приведены так называемые «десятичные приставки», которые используются не только с байтами, но и в других областях человеческой деятельности. Например, приставка «кило» в слове «килобайт» означает тысячу байт, также как в случае с километром она соответствует тысяче метров, а в примере с килограммом она равна тысяче грамм.
Продолжение следует…
Возникает вопрос: есть ли продолжение у таблицы байтов? В математике есть понятие бесконечности, которое обозначается как перевернутая восьмерка: ∞.
Понятно, что в таблице байтов можно и дальше добавлять нули, а точнее, степени к числу 10 таким образом: 10 27 , 10 30 , 10 33 и так до бесконечности. Но зачем это надо? В принципе, пока хватает терабайт и петабайт. В будущем, возможно, уже мало будет и йоттабайта.
Напоследок парочка примеров по устройствам, на которые можно записать терабайты и гигабайты информации.
Есть удобный «терабайтник» – внешний жесткий диск, который подключается через порт USB к компьютеру. На него можно записать терабайт информации. Особенно удобно для ноутбуков (где смена жесткого диска бывает проблематична) и для резервного копирования информации. Лучше заранее делать резервные копии информации, а не после того, как все пропало.
Флешки бывают 1 Гб, 2 Гб, 4 Гб, 8 Гб, 16 Гб, 32 Гб , 64 Гб и даже 1 терабайт.
CD-диски могут вмещать 650 Мб, 700 Мб, 800 Мб и 900 Мб.
DVD-диски рассчитаны на большее количество информации: 4.7 Гб, 8.5 Гб, 9.4 Гб и 17 Гб.
Упражнения по компьютерной грамотности
Статья закончилась, но можно еще прочитать:
Содержание
- Степени двойки
- Степени двойки таблица
- Двоичная система для чайников
- Нейронные сети. Формулы обратного распространения
- Нейронные сети. Обратное распространение ошибки
- Нейронные сети. Градиентный спуск: как учатся нейронные сети
- Нейронные сети. Просто о сложном
- Карты наук
- За день до экзамена
- Степени двойки информатика 7 класс
- Степени двойки таблица
- Как пользоваться таблицей степеней числа два?
- Примеры использования таблицы степеней числа два
- Калькулятор степеней
- Таблица степеней от 1 до 10
- Таблица степеней от 1 до 10
- Теория
- Таблица степеней 2 (двойки) от 0 до 32
- Как пользоваться таблицей степеней числа два?
- Примеры использования таблицы степеней числа два
Степени двойки
Этот вспомогательный материал, который может быть полезен для подготовки к ГИА по информатике, в частности задач 15 ГИА, задач 1 ГИА, B10 ЕГЭ по информатике
Степени двойки таблица
| 2 0 | 1 |
| 2 1 | 2 |
| 2 2 | 4 |
| 2 3 | 8 |
| 2 4 | 16 |
| 2 5 | 32 |
| 2 6 | 64 |
| 2 7 | 128 |
| 2 8 | 256 |
| 2 9 | 512 |
| 2 10 | 1024 |
| 2 11 | 2048 |
| 2 12 | 4096 |
| 2 13 | 8192 |
| 2 14 | 16384 |
| 2 15 | 32768 |
| 2 16 | 65536 |
| 2 17 | 131072 |
| 2 18 | 262144 |
| 2 19 | 524288 |
| 2 20 | 1048576 |
Автор: Александр Чернышов
Оцените статью, это очень поможет развитию сайта.
Источник
Двоичная система для чайников
Я решил сделать серию постов по информатике для чайников.
Если первый пост пойдёт хорошо, то будет еще несколько в том же духе.
Чтобы провести хирургическую операцию, анатомию знать не обязательно, но вот результаты будут непредсказуемы. Точно так же, чтобы программировать, не обязательно знать, как компьютер устроен изнутри, но иногда такое незнание может привести к душераздирающим последствиям.
Основа основ современного компьютера – ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ (2-СС). Звучит угрожающе. Чтобы понять, что такое ДСС, и научиться с ней работать, надо уметь складывать, умножать и возводить числа в степень. Ок, даю шпаргалку.
Пусть у нас есть какое-то число. Допустим, 5. И мы хотим прибавить к нему другое число. Допустим, 3. Как нам это сделать? Давайте, представим число 5 как пять палочек:
А число 3 как три палочки:
Чтобы сложить их, сначала нарисуем пять палочек, потом допишем к ним еще три:
Теперь пересчитаем – получилось 8.
Зря смеётесь! Когда считаем палочками – в Википедии это называется (ВНИМАНИЕ! НЕНОРМОТИВНАЯ ЛЕКСИКА!) «Единичная непозиционная система счисления с единичным весовым коэффициентом». Ну, или попросту будем называть УНАРНАЯ СИСТЕМА СЧИСЛЕНИЯ (1-СС).
В обычной жизни мы (люди) пользуемся ДЕСЯТЕРИЧНОЙ СИСТЕМОЙ СЧИСЛЕНИЯ (10-СС). Она так называется, потому что у нас есть десять цифр. К тому же, она еще и ПОЗИЦИОННАЯ, что означает, что значение (вес) цифры зависит от её положения в записи числа, например, в числах 2, 21 и 211 цифра 2 означает, соответственно, единицы, десятки и сотни.
Десятичная система счисления
Как мы складываем в 10-СС? Например, столбиком:
Сначала складываем единицы: 2+9 = 11, т.е. при сложении двух единичных чиселок появился новый десяток. Ясное дело, что из них может появиться только один десяток, потому что самое большое, что можно сложить – это 9+9 = 18. Таким образом, разбиваем сложение на кусочки: вместо 12+99 мы делаем 2+9 + 10+90, т.е. единицы и десятки (а потом и сотни) складываем отдельно друг от друга:
12 + 99 = [разобьем на разряды]
= (2+9) + (10+90) = [сложим первые разряды]
= 11 + (10+90) = [снова разобьем на десятки и единицы]
= (1 + 10) + (10 + 90) = [снова перегруппируем, чтобы отделить десятки от единиц]
= 1 + (10 + 10 + 90) = [сложим десятки]
= 1 + (110) = [разобьем на сотни и десятки]
Ясно, что получится 111, но давайте остановимся и посмотрим на эту полученную форму записи:
Фишка в том, что любое число можно представить как сумму отдельно единиц, отдельно десятков, сотен и т.д., например:
564 = 500 + 60 + 4, 7031 = 7000 + 000 + 30 + 1
Особенность такой записи в том, что мы видим во всех разрядах одну значащую цифру (первую), все следующие за ней цифры – это нули. Запомните этот момент – это важно.
При этом вместо того, чтобы писать 1000, мы можем написать 10^3 (т.е. десять в третьей степени, что можно расшифровать как 10*10*10).
7000 = 7*1000 = 7 * 10^3
А всё число 7031 можно расписать так:
7031 = 7*10^3 + 0*10^2 + 3*10^1 + 1*10^0
Напомню, что любое число в нулевой степени даёт единицу, и 10^0 = 1, а любое число в первой степени даёт само себя 10^1 = 10. Еще напомню, что любое число умноженное на 0 даёт 0, т.е. 0*10^2 = 0.
Так вот, наша система счисления называется десятичной именно благодаря этой десятке, которую в степень возводим.
Краткое отступление. Дорогие мои! Не путайте числа и цифры! Путать цифры и числа – это как путать буквы и звуки. Цифра – это просто символ для записи чисел. А число – это абстрактная величина, обычно означающее количество чего-нибудь. Думаю, все поняли. 🙂
Двоичная система счисления
Теперь, поговорим о 2-СС. Её особенность в том, что в ней есть всего 2 символа для записи чисел: 0 и 1. Что интересно, при этом любое число, которое можно записать в 10-СС, так же можно записать и в 2-СС, и даже в 1-СС!
Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:
101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0
= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)
Теперь давайте поскладываем в двоичной системе.
Начнём с простого: 0+0 = 0, 1+0 = 1, 0+1 = 1
Ничего удивительного, в 10-СС это точно так же выглядит.
Теперь посложнее: 1 + 1 = 10
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Нет. Это не десять плюс один! Это два плюс один! В 10-СС это выглядит так: 2 + 1 = 3, а в 1-СС так: || + | = |||. Ясно –понятно?
Хм… сложновато? Давайте упростим! По той же схеме, что и 12 + 99. Не забываем, что всё это в двоичной системе!
11 + 1 = [разобьем на разряды]
= (10 + 1) + 1 = [перегруппируем]
= 10 + (1 + 1) = [О! “1+1” складывать умеем!]
= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]
Ну, сколько можно. Это не СТО. Если то же самое записать в 10-СС, то получим: 3 + 1 = 4. Т.е. это 100 в записи 2-СС – это ЧЕТЫРЕ.
Ну, и для закрепления материала сложим в 2-СС:
= (1000 + 100 + 00 + 1) + (1000 + 000 + 00 + 1)
= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)
= (10000) + (100) + (00) + (10)
= (10000) + (100) + (00 + 10)
А по-русски: 13 + 9 = 22
Большое спасибо! Очень хорошо объяснили. Всё понял.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи. И дальше нет объяснения почему и как. Естественно дальше идут примеры сложнее, но т.к. этот простой непонятен. Дальше залазить в дебри
поделитесь, пожалуйста, еще постами по информатике если есть
А теперь слушайте домашнее задание: построить синхрофазотрон.
Теперь посложнее: 1 + 1 = 10
Ой! Почему десять.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Я тебя разочарую, но это десять и есть.
Кстати цифровая схемотехника основана на двоичной системе счисления. На основных законах булевой алгебры. 1+1=1 1+0=1 1*1=1 1*1=0
На самом деле все еще проще.
Нейронные сети. Формулы обратного распространения
Представляем заключительную лекцию из курса по нейронным сетям от 3blue1brown. В этой лекции речь пойдет о формулах обратного распространения. Одной из важных тем, которая позволит разобраться с основными моментами дифференцирования сложных функций в контексте сетей.
Благодарим за создание выпуска:
Переводчика – Федора Труфанова;
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
Нейронные сети. Обратное распространение ошибки
Привет, Лига образования!
Мы продолжаем переводить легендарный курс по нейросетям от 3blue1brown.
В предыдущей лекции мы узнали о градиентном спуске. Сегодня речь пойдет о методе обратного распространения — главном алгоритме обучения нейронных сетей.
Благодарим за создание выпуска:
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
И бонус в комментариях, английский!
Нейронные сети. Градиентный спуск: как учатся нейронные сети
Обучение — сложный процесс не только для человека, но и для сущностей, порожденных разумом человека.
Мы подготовили долгожданное продолжение лекций по нейросетям. Градиентный спуск: как учатся нейронные сети.
Благодарим за участие в выпуске:
Редакторов – Дмитрия Титова, Михаила Коротеева, Дмитрия Мирошниченко;
Корректора – Дмитрия Мирошниченко;
Дикторов – Никифора Стасова, Дарью Яговкину;
Монтажера – Олега Жданова.
Разговор о системах счисления:
— Программист подарил своей женщине 5 роз, сказав «эта 101 роза тебе» (двоичная). Пещерный человек, подарил бы три розы, сказав «бери эти 111 роз» (унарная).
— То есть неандертальца от программиста отличает всего лишь ноль?
— Ну вообще введение 0 было огромным шагом для математики. Можно сказать первый мощный шаг к абстрактному мышлению. Так что в какой-то степени да, «0» — это переходная ступень между неандертальцем и программистом.
Нейронные сети. Просто о сложном
Привет, Пикабу. Сегодня у нас кое-что действительно классное для Лиги образования.
Мы договорились о переводе и озвучке с автором самых крутых на Youtube видео про математику-информатику-физику.
И наша первая озвучка — видео о том, что же такое нейросети.
За это отличную озвучку мы благодарим Александра Колдаева.
Если хочешь поучаствовать в переводе или озвучке — напиши нам в вк, телеграм или facebook.
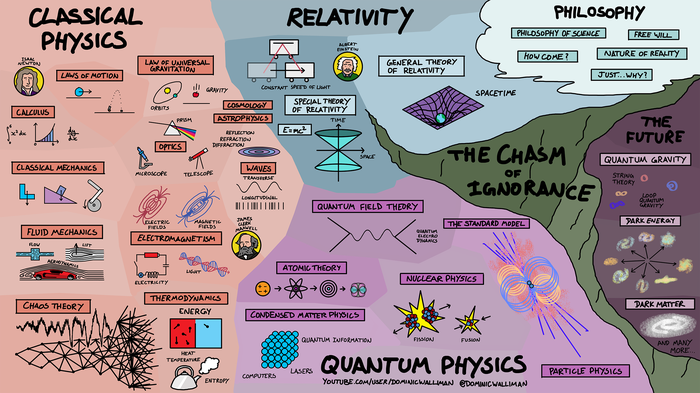
Карты наук
Выше был их автор. А вот и одна из его карт (по физике):
О карте, нарисованной выше, Dominic подробно рассказал в следующем видео. Он рассказал о ранней физике, об Эйнштейне и его теориях специальной и общей относительности, и о подвидах квантовой физики.
Кстати говоря, помимо карт наук, на его странице во flickr есть интересные постеры о том, как мы уже сейчас используем квантовые технологии.
Все его видео по картам наук публикуются в следующем плейлисте: https://www.youtube.com/playlist?list=PLOYRlicwLG3St5aEm02nc.
Они на английском, но уже есть и переводы.
Вот, например, по Computer Science:
А вот по математике:
Спасибо за внимание!
За день до экзамена
Ну, может и не сильно-то ждёт. Ну да ладно, всё равно любит. Наверное.
Источник
Степени двойки информатика 7 класс
Этот вспомогательный материал, который может быть полезен для подготовки к ГИА по информатике, в частности задач 15 ГИА, задач 1 ГИА, B10 ЕГЭ по информатике
Степени двойки таблица
2 0
| 1 | |
| 2 1 | 2 |
| 2 2 | 4 |
| 2 3 | 8 |
| 2 4 | 16 |
| 2 5 | 32 |
| 2 6 | 64 |
| 2 7 | 128 |
| 2 8 | 256 |
| 2 9 | 512 |
| 2 10 | 1024 |
| 2 11 | 2048 |
| 2 12 | 4096 |
| 2 13 | 8192 |
| 2 14 | 16384 |
| 2 15 | 32768 |
| 2 16 | 65536 |
| 2 17 | 131072 |
| 2 18 | 262144 |
| 2 19 | 524288 |
| 2 20 | 1048576 |
Автор: Александр Чернышов
Оцените статью, это очень поможет развитию сайта.
Ниже представлена таблица степеней числа 2. Она даст нам представление необходимого числа бит, которое нам необходимо для хранения чисел.
Как пользоваться таблицей степеней числа два?
| Степень двойки (n) | Значение степени двойки 2 n |
Максимальное число без знака, записанное с помощью n бит |
|
| 1 | – | – | |
| 1 | 2 | 1 | – |
| 2 | 4 | 3 | 1 |
| 3 | 8 | 7 | 3 |
| 4 | 16 | 15 | 7 |
| 5 | 32 | 31 | 15 |
| 6 | 64 | 63 | 31 |
| 7 | 128 | 127 | 63 |
| 8 | 256 | 255 | 127 |
| 9 | 512 | 511 | 255 |
| 10 | 1 024 | 1 023 | 511 |
| 11 | 2 048 | 2 047 | 1023 |
| 12 | 40 96 | 4 095 | 2047 |
| 13 | 8 192 | 8 191 | 4095 |
| 14 | 16 384 | 16 383 | 8191 |
| 15 | 32 768 | 32 767 | 16383 |
| 16 | 65 536 | 65 535 | 32767 |
| 17 | 131 072 | 131 071 | 65 535 |
| 18 | 262 144 | 262 143 | 131 071 |
| 19 | 524 288 | 524 287 | 262 143 |
| 20 | 1 048 576 | 1 048 575 | 524 287 |
| 21 | 2 097 152 | 2 097 151 | 1 048 575 |
| 22 | 4 194 304 | 4 194 303 | 2 097 151 |
| 23 | 8 388 608 | 8 388 607 | 4 194 303 |
| 24 | 16 777 216 | 16 777 215 | 8 388 607 |
| 25 | 33 554 432 | 33 554 431 | 16 777 215 |
| 26 | 67 108 864 | 67 108 863 | 33 554 431 |
| 27 | 134 217 728 | 134 217 727 | 67 108 863 |
| 28 | 268 435 456 | 268 435 455 | 134 217 727 |
| 29 | 536 870 912 | 536 870 911 | 268 435 455 |
| 30 | 1 073 741 824 | 1 073 741 823 | 536 870 911 |
| 31 | 2 147 483 648 | 2 147 483 647 | 1 073 741 823 |
| 32 | 4 294 967 296 | 4 294 967 295 | 2 147 483 647 |
Примеры использования таблицы степеней числа два
Например, нам необходимо узнать, в какую степень нужно возвести число 2, чтобы получить 256. Во втором столбце находим число 256 и считываем, что 256 это два в степени восемь.
Аналогично, 2 в 11 степени равно 2048.
2 в 13 степени равно 8,192.
2 в 15 степени равно 32,768
2 в 17 степени равно 131,072
Таблица степеней чисел с 1 до 10. Калькулятор степеней онлайн. Интерактивная таблица и изображения таблицы степеней в высоком качестве.
Калькулятор степеней
С помощью данного калькулятора вы сможете в режиме онлайн вычислить степень любого натурального числа. Введите число, степень и нажмите кнопку «вычислить».
Таблица степеней от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 n | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 n | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4 n | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5 n | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6 n | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7 n | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8 n | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9 n | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10 n | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Таблица степеней от 1 до 10
10 10 = 10000000000
Теория
Степень числа – это сокращенная запись операции многократного умножения числа самого на себя. Само число в данном случае называется – основанием степени, а количество операций умножения – показателем степени.
запись читается: «a» в степени «n».
«a» – основание степени
«n» – показатель степени
4 6 = 4 × 4 × 4 × 4 × 4 × 4 = 4096
Данное выражение читается: 4 в степени 6 или шестая степень числа четыре или возвести число четыре в шестую степень.
Источник
Таблица степеней 2 (двойки) от 0 до 32
Ниже представлена таблица степеней числа 2. Она даст нам представление необходимого числа бит, которое нам необходимо для хранения чисел.
Как пользоваться таблицей степеней числа два?
| Степень двойки (n) | Значение степени двойки 2 n |
Максимальное число без знака, записанное с помощью n бит |
|
| 0 | 1 | — | — |
| 1 | 2 | 1 | — |
| 2 | 4 | 3 | 1 |
| 3 | 8 | 7 | 3 |
| 4 | 16 | 15 | 7 |
| 5 | 32 | 31 | 15 |
| 6 | 64 | 63 | 31 |
| 7 | 128 | 127 | 63 |
| 8 | 256 | 255 | 127 |
| 9 | 512 | 511 | 255 |
| 10 | 1 024 | 1 023 | 511 |
| 11 | 2 048 | 2 047 | 1023 |
| 12 | 40 96 | 4 095 | 2047 |
| 13 | 8 192 | 8 191 | 4095 |
| 14 | 16 384 | 16 383 | 8191 |
| 15 | 32 768 | 32 767 | 16383 |
| 16 | 65 536 | 65 535 | 32767 |
| 17 | 131 072 | 131 071 | 65 535 |
| 18 | 262 144 | 262 143 | 131 071 |
| 19 | 524 288 | 524 287 | 262 143 |
| 20 | 1 048 576 | 1 048 575 | 524 287 |
| 21 | 2 097 152 | 2 097 151 | 1 048 575 |
| 22 | 4 194 304 | 4 194 303 | 2 097 151 |
| 23 | 8 388 608 | 8 388 607 | 4 194 303 |
| 24 | 16 777 216 | 16 777 215 | 8 388 607 |
| 25 | 33 554 432 | 33 554 431 | 16 777 215 |
| 26 | 67 108 864 | 67 108 863 | 33 554 431 |
| 27 | 134 217 728 | 134 217 727 | 67 108 863 |
| 28 | 268 435 456 | 268 435 455 | 134 217 727 |
| 29 | 536 870 912 | 536 870 911 | 268 435 455 |
| 30 | 1 073 741 824 | 1 073 741 823 | 536 870 911 |
| 31 | 2 147 483 648 | 2 147 483 647 | 1 073 741 823 |
| 32 | 4 294 967 296 | 4 294 967 295 | 2 147 483 647 |
Примеры использования таблицы степеней числа два
Например, нам необходимо узнать, в какую степень нужно возвести число 2, чтобы получить 256. Во втором столбце находим число 256 и считываем, что 256 это два в степени восемь.
Аналогично, 2 в 11 степени равно 2048.
2 в 13 степени равно 8,192.
2 в 15 степени равно 32,768
2 в 17 степени равно 131,072
Источник
Таблица степеней 2 (двойки) от 0 до 32
Приведенная таблица кроме степени двойки показывает максимальные числа, которые может хранить компьютер для заданного числа бит. Причем как для целых так и чисел со знаком.
Исторически сложилось, что компьютеры используют двоичную систему счисления, а, соответственно, и хранения данных. Таким образом, любое число можно представить как последовательность нулей и единиц (бит информации). Существует несколько способов представления чисел в виде двоичной последовательности.
Рассмотрим наиболее простой из них – это целое положительное число. Тогда чем больше число нам нужно записать, тем более длинная последовательность бит нам необходима.
Ниже представлена таблица степеней числа 2. Она даст нам представление необходимого числа бит, которое нам необходимо для хранения чисел.
Как пользоваться таблицей степеней числа два?
Первый столбец – это степень двойки, который одновременно, обозначает число бит, которое представляет число.
Второй столбец – значение двойки в соответствующей степени (n).
Пример нахождения степени числа 2. Находим в первом столбце число 7. Смотрим по строке вправо и находим значение два в седьмой степени (27) – это 128
Третий столбец – максимальное число, которое можно представить с помощью заданного числа бит (в первом столбце).
Пример определения максимального целого числа без знака. Если использовать данные из предыдущего примера, мы знаем, что 27 = 128. Это верно, если мы хотим понять, какое количество чисел, можно представить с помощью семи бит. Но, поскольку первое число – это ноль, то максимальное число, которое можно представить с помощью семи бит 128 – 1 = 127 . Это и есть значение третьего столбца.
| Степень двойки (n) |
Значение степени двойки 2n |
Максимальное число без знака,
записанное с помощью n бит
|
Максимальное число со знаком, записанное с помощью n бит |
| 0 | 1 | – | – |
| 1 | 2 | 1 | – |
| 2 | 4 | 3 | 1 |
| 3 | 8 | 7 | 3 |
| 4 | 16 | 15 | 7 |
| 5 | 32 | 31 | 15 |
| 6 | 64 | 63 | 31 |
| 7 | 128 | 127 | 63 |
| 8 | 256 | 255 | 127 |
| 9 | 512 | 511 | 255 |
| 10 | 1 024 | 1 023 | 511 |
| 11 | 2 048 | 2 047 | 1023 |
| 12 | 40 96 | 4 095 | 2047 |
| 13 | 8 192 | 8 191 | 4095 |
| 14 | 16 384 | 16 383 | 8191 |
| 15 | 32 768 | 32 767 | 16383 |
| 16 | 65 536 | 65 535 | 32767 |
| 17 | 131 072 | 131 071 | 65 535 |
| 18 | 262 144 | 262 143 | 131 071 |
| 19 | 524 288 | 524 287 | 262 143 |
| 20 | 1 048 576 | 1 048 575 | 524 287 |
| 21 | 2 097 152 | 2 097 151 | 1 048 575 |
| 22 | 4 194 304 | 4 194 303 | 2 097 151 |
| 23 | 8 388 608 | 8 388 607 | 4 194 303 |
| 24 | 16 777 216 | 16 777 215 | 8 388 607 |
| 25 | 33 554 432 | 33 554 431 | 16 777 215 |
| 26 | 67 108 864 | 67 108 863 | 33 554 431 |
| 27 | 134 217 728 | 134 217 727 | 67 108 863 |
| 28 | 268 435 456 | 268 435 455 | 134 217 727 |
| 29 | 536 870 912 | 536 870 911 | 268 435 455 |
| 30 | 1 073 741 824 | 1 073 741 823 | 536 870 911 |
| 31 | 2 147 483 648 | 2 147 483 647 | 1 073 741 823 |
| 32 | 4 294 967 296 | 4 294 967 295 | 2 147 483 647 |
Необходимо принять во внимание, что не все числа в компьютере представлены таким образом. Существуют и другие способы представления данных. Например, если мы хотим записывать не только положительные, но и отрицательные числа, то нам потребуется еще один бит для хранения значения “плюс/минус”. Таким образом, количество бит, предназначенных для хранения чисел у нас уменьшилось на один. Какое максимальное число может быть записано в виде целого числа со знаком можно посмотреть в четвертом столбце.
Для этого же самого примера ( 27 ) семью битами можно записать максимум число +63, поскольку один бит занят знаком “плюс”. Но мы можем хранить и число “-63“, что было бы невозможно, если бы все биты были бы зарезервированы под хранение числа.
Примеры использования таблицы степеней числа два
Например, нам необходимо узнать, в какую степень нужно возвести число 2, чтобы получить 256. Во втором столбце находим число 256 и считываем, что 256 это два в степени восемь.
Аналогично, 2 в 11 степени равно 2048.
2 в 13 степени равно 8,192.
2 в 15 степени равно 32,768
2 в 17 степени равно 131,072
0
Хранение и кодирование информации |
Описание курса
| Использование электронных таблиц Excel