|
Понятие “Кратность” означает делимость на определённое число. В нашем случае, числа, которые будут кратны 10, должны делиться на данное число без остатка. Вспомним признак делимости на 10 – число делится на 10 в том случае, если у него последняя цифра равна нулю. Поэтому все числа с последней цифрой “0” будут кратны 10. Примеры этих чисел Двухзначные числа: 10 (10*1), 20 (10*2), 30 (10*3), 40 (10*4), 50 (10*5), 60 (10*6), 70 (10*7), 80 (10*8), 90 (10*9). Трёхзначные числа: 100 (10*10), 110 (10*11), 120 (10*12), 200 (10*20), 300 (10*30)… Четырёхзначные числа: 1000 (10*100), 1500 (10*150), 2000 (10*200), 2500 (10*250), 3000 (10*300), 4000 (10*400)… Такие числа, как: миллион, миллиард или триллион также кратны 10. система выбрала этот ответ лучшим Ninaarc 5 лет назад Любое число можно разделить на другое число, при этом в результате деления может получиться либо целое число, либо дробное. Нас интересуют числа, которые делятся без остатка, поскольку понятие “кратность” как раз и предполагает делимость на какое-нибудь число без остатка. Теперь нам нужно вспомнить признаки делимости, в частности: признак делимости чисел на 10. Число может быть без остатка разделено на 10 только в том случае, если оно оканчивается на ноль. Отсюда следует, что числами, кратными 10, будут все те, которые имеют 0 в конце. А самым маленьким числом, кратным 10 является число 10. Примеры чисел, кратных 10: 50, 110, 370, 2740, 50100, 857000, 1600000. владсандрович 5 лет назад Кратность само по себе как определение, говорит о том, что такие числа, должны делиться на цифру десять, которая у нас есть в вопросе без остатка. А по законам математики, что бы такое было возможным, необходимо то, что бы эти числа, заканчивались на ноль, а именно : 20, 90, 50, 150, которые все будут делиться на десять без остатка. Nelli4ka 5 лет назад Что мы понимаем под словом “кратность”? Кратность – это способность одного числа делиться на другое число (в нашем случае это 10) так, чтобы не было остатка. Какие же числа кратны 10? Такие, на конце которых есть ноль. Они могут быть двухзначными (10, 20, 30 и так далее до 90), трехзначными (100, 200, 300 и так далее до 900), четырехзначными и так до бесконечности. Алиса в Стране 5 лет назад Мы все помним, что такое для числа быть кратным какому то другому числу. Это означает “способность” делится на него без остатка. Чисел, кратных 10 (десяти) существует огромное множество, начиная от самого этого числа – десять и до бесконечности, это все те числа, у которых справа есть хотя-бы один ноль: 10, 20, 30, …..10000, …..10000000 и так далее. Profilaktika 5 лет назад В десятичной системе счисления (как я понимаю, речь именно о ней) числа, кратные 10, определить очень просто – К тому же являются натуральными числами, это немаловажное уточнение. Они должны делиться на десять, не образуя остаток от деления, т.е. в результате должно получаться целое натуральное число. РУДЬКО 5 лет назад Касаемо того, какие числа кратны 10, то есть какие числа делятся без остатка на 10, то тут есть обычное простое правило, которое гласит, что все целые числа, которые заканчиваются на “0” кратны 10, то есть делятся на 10 без остатка. Например, 10, 20, 30, 450, 12450 и так далее и тому подобное. Кратны 10, то есть делятся без остатка на 10, те целые числа (положительные и отрицательные), которые при записи в десятичной системе счисления заканчиваются цифрой “0”. Для деления такого числа на 10 достаточно убрать этот последний ноль. Медвед 9 лет назад Натуральные числа кратные 10 – это натуральные числа, которые делятся на 10 без остатка. Такие числа нетрудно определить по внешнему виду: у натуральных чисел, кратных десяти, самая правая цифра всегда ноль. Кратны десяти все числа начиная от двузначных и больше, у которых правая цифра в числе (разряд единиц) равна нулю. Например: 10, 40, 560, 12300 и так далее. Кратно – это значит делится на 10 без остатка. Те числа которые делятся на 10 Эти сисла должны заканчиватся на 0 Это,к поимеру:210,370,580 670 и т.д. и т.п. Это числа,которые делятся на 10 Они должны оканчиватся на 0 К примеру: 100 120 130 500 450 И тд Сергей0 9 лет назад Все, что делится на 10 без остатка. 10, 100, 110, 1 000 010 и далее Oleg74 9 лет назад Числа , оканчивающиеся на цифру 0 и есть числа , кратные 10. То есть это такие числа : 10, 20, 30, 40, 50, 60, 70, 80, 90 , 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200 … 1000, 1110, 1120, 1130 … и т.д. Знаете ответ? |
Кратность – математический термин, который обозначает особое соотношение двух чисел между собой. При этом определенное число может быть кратным одному или одновременно нескольким числам.

Термин «кратность» относится к области математики: с точки зрения этой науки, он означает количество раз, которое определенное число входит в состав другого числа.
Упрощая приведенное определение, можно сказать, что кратность одного числа по отношению к другому показывает, во сколько раз первое число больше второго. Таким образом, тот факт, что одно число является кратным другому фактически означает, что большее из них способно быть разделенным на меньшее без остатка. Например, кратным числу 3 является 6.
Такое понимание термина «кратность» влечет за собой выведение из него нескольких важных следствий. Первое из них – то, что любое число может иметь неограниченное количество кратных ему чисел. Это связано с тем, что фактически для того, чтобы получить кратное некоторому числу другое число, необходимо первое из них умножить на любое целое положительное значение, которых, в свою очередь, имеется бесконечное множество. Например, кратными числу 3 являются числа 6, 9, 12, 15 и другие, получаемые умножением числа 3 на любое целое положительное число.
Второе важное свойство касается определения наименьшего целого числа, являющегося кратным рассматриваемому. Так, наименьшим кратным по отношению к любому числу является само это число. Это связано с тем, что наименьшим целым результатом деления одного числа на другое является единица, а именно деление числа само на себя и обеспечивает этот результат. Соответственно, число, кратное рассматриваемому, не может быть меньше, чем само это число. Например, для числа 3 наименьшим кратным числом будет 3. При этом определить наибольшее число, кратное рассматриваемому, фактически невозможно.
Числа, кратные 10, обладают всеми перечисленными свойствами наравне с другими кратными числами. Так, из перечисленных свойств следует, что наименьшим числом, кратным 10, является само число 10. При этом, поскольку число 10 является двузначным, можно сделать вывод, что кратным числу 10 могут быть только числа, состоящие не менее чем из двух знаков.
Для того чтобы получить другие числа, кратные 10, необходимо число 10 умножить на любое целое положительное число. Таким образом, в перечень чисел, кратных 10, войдут числа 20, 30, 40, 50 и так далее. Следует обратить внимание, что все полученные числа должны без остатка делиться на 10. При этом определить наибольшее число, кратное 10, как и в случаях с другими числами, невозможно.
Кроме того, обратите внимание, что существует простой практический способ определить, является ли конкретное рассматриваемое число кратным 10. Для этого следует выяснить, какова его последняя цифра. Так, если она равна 0, рассматриваемое число будет кратным 10, то есть может быть без остатка разделено на 10. В противном случае число не является кратным 10.
Источники:
- Делители и кратные числа
Кратные числа, калькулятор
Кратное число – это число, делащееся на данное целое число без остатка; например 12 кратно 3.
Найти, вычислить кратные с калькулятором
Кратное – это произведение целого числа на любое другое целое число. Например, первые шесть чисел, кратных 3: 3, 6, 9, 12, 15 и 18. Это легко проверить на примерах ниже:
3 x 1 = 3 ;
3 x 2 = 6 ;
3 x 3 = 9 ;
3 x 4 = 12 ;
3 x 5 = 15 ;
3 x 6 = 18.
Два и более чисел могут иметь общие кратные. Например, наименьшее общее кратное (НОК) 3 и 7 равно 21, т. е. произведению этих двух чисел.
Наглядная таблица чисел кратных 3
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
– Кратные 3
Термин «кратность» относится к области математики: с точки зрения этой науки, он означает количество раз, которое определенное число входит в состав другого числа.
Понятие кратности
Такое понимание термина «кратность» влечет за собой выведение из него нескольких важных следствий. Первое из них — то, что любое число может иметь неограниченное количество кратных ему чисел. Это связано с тем, что фактически для того, чтобы получить кратное некоторому числу другое число, необходимо первое из них умножить на любое целое положительное значение, которых, в свою очередь, имеется бесконечное множество. Например, кратными числу 3 являются числа 6, 9, 12, 15 и другие, получаемые умножением числа 3 на любое целое положительное число.
Второе важное свойство касается определения наименьшего целого числа, являющегося кратным рассматриваемому. Так, наименьшим кратным по отношению к любому числу является само это число. Это связано с тем, что наименьшим целым результатом деления одного числа на другое является единица, а именно деление числа само на себя и обеспечивает этот результат. Соответственно, число, кратное рассматриваемому, не может быть меньше, чем само это число. Например, для числа 3 наименьшим кратным числом будет 3. При этом определить наибольшее число, кратное рассматриваемому, фактически невозможно.
Числа, кратные 10
Числа, кратные 10, обладают всеми перечисленными свойствами наравне с другими кратными числами. Так, из перечисленных свойств следует, что наименьшим числом, кратным 10, является само число 10. При этом, поскольку число 10 является двузначным, можно сделать вывод, что кратным числу 10 могут быть только числа, состоящие не менее чем из двух знаков.
Для того чтобы получить другие числа, кратные 10, необходимо число 10 умножить на любое целое положительное число. Таким образом, в перечень чисел, кратных 10, войдут числа 20, 30, 40, 50 и так далее. Следует обратить внимание, что все полученные числа должны без остатка делиться на 10. При этом определить наибольшее число, кратное 10, как и в случаях с другими числами, невозможно.
Кроме того, обратите внимание, что существует простой практический способ определить, является ли конкретное рассматриваемое число кратным 10. Для этого следует выяснить, какова его последняя цифра. Так, если она равна 0, рассматриваемое число будет кратным 10, то есть может быть без остатка разделено на 10. В противном случае число не является кратным 10.
Признаки делимости на 10, 100, 1 000 и так далее: примеры, доказательства
Продолжаем разговор о признаках делимости. В этом материале мы изучим, по каким признакам можно определить делимость числа на 1000 , 100 и т.д. В первом пункте сформулируем их, возьмем несколько примеров, после чего приведем необходимые доказательства. Ближе к концу мы разберем доказательства делимости на 1000 , 100 , 10 с помощью математической индукции и формулы бинома Ньютона.
Формулировка признака делимости на 10 , 100 и т.д. с примерами
Сначала запишем формулировку признака делимости на десять:
Если число заканчивается на 0 , то его можно разделить на 10 без остатка, а если на любую другую цифру, то нельзя.
Теперь запишем признак делимости на 100 :
На 100 без остатка можно разделить такое число, которое заканчивается двумя нулями. Если хотя бы одна из двух цифр в конце не равна нулю, то такое число разделить на 100 без остатка нельзя.
Точно так же можно вывести признаки делимости на тысячу, 10 тысяч и так далее: в зависимости от количества нулей в делителе нам требуется соответствующее количество нулей в конце числа.
Отметим, что данные признаки нельзя распространить на 0 , поскольку 0 можно разделить на любое целое число – и на сто, и на тысячу, и на десять тысяч.
Эти признаки легко применять в решении задач, ведь подсчитать количество нулей в исходном числе несложно. Возьмем несколько примеров применения данных правил на практике.
Условие: определите, какие числа из ряда 500 , − 1 010 , − 50 012 , 440 000 300 000 , 67 893 можно разделить на 10 , 10 000 без остатка, а какие из них не делятся на 100 .
Решение
Согласно признаку делимости на 10 , мы можем совершить такое действие с тремя числами из указанных, а именно с − 1 010 , 440 000 300 000 , 500 , ведь они все заканчиваются нулями. А вот для − 50 012 и 67 893 такого деления без остатка мы осуществить не можем, поскольку у них в конце стоят 2 и 3 .
На 10 тысяч здесь можно разделить всего одно число – 440 000 300 000 , поскольку лишь в нем достаточно нулей в конце ( 4 ) . Зная признак делимости на 100 , можно сказать, что − 1 010 , − 50 012 и 67 893 на сотню не делятся, поскольку в конце у них нет двух нулей.
Ответ: на 10 можно разделить числа 500 , − 1 010 , 440 000 300 000 ; на 10 000 – число 440 000 300 000 ; на 100 не делятся числа 1 010 , − 50 012 и 67 893 .
Как доказать признаки делимости на 10 , 100 , 1000 и др.
Для доказательства нам потребуется вспомнить, как правильно умножать натуральные числа на 100 , 10 и т.д., а также вспомнить, что из себя вообще представляет понятие делимости и какими свойствами оно обладает.
Сначала приведем доказательство признака делимости числа на 10 . Для удобства запишем его в виде теоремы, то есть представим как необходимое и достаточное условие.
Чтобы определить, делится ли целое число на 10 , нужно посмотреть на его конечную цифру. Если она равна 0 , то такое деление без остатка возможно, если она представляет из себя другую цифру, то нет.
Начнем с доказательства необходимости данного условия. Допустим, нам известно, что некое число a можно разделить на 10 . Докажем, что в конце у него стоит 0 .
Поскольку a можно разделить на 10 , то согласно самому понятию делимости, должно существовать такое целое число q , при котором будет верным равенство a = 10 · q . Вспомним правило умножения на 10 : произведение 10 · q должно быть целым числом, запись которого можно получить, если дописать к q справа нуль. Значит, в записи числа a = 10 · q последним будет стоять 0 . Необходимость можно считать доказанной, далее нам нужно доказать достаточность.
Допустим, что у нас есть целое число с 0 на конце. Докажем, что оно делится на 10 . Если последняя цифра целого числа равна нулю, то исходя из правила умножения на 10 , его можно представить в виде a = a 1 · 10 . Здесь число a 1 получается из a , в котором убрали последнюю цифру. По определению делимости из равенства a = a 1 · 10 будет следовать делимость a на 10 . Таким образом мы доказали достаточность условия.
Точно так же доказываются и другие признаки делимости – на 100 , 1000 и т.д.
Прочие случаи делимости на 1000 , 100 , 10 и др.
В данном пункте мы расскажем о других способах определения делимости на 10 . Так, если изначально у нас задано не число, а буквенное выражение, то воспользоваться указанными выше признаками мы не можем. Здесь нужно применить другие методы решения.
Первым таким методом является использование формулы бинома Ньютона. Решим такую задачу.
Условие: определите, можно ли разделить 11 n + 20 n — 21 на 10 при любом натуральном значении n .
Решение
Cначала представим 11 как сумму 10 и единицы, а потом воспользуемся нужной формулой.
11 n + 20 n — 21 = ( 10 + 1 ) n + 20 n — 21 = = C n 0 · 10 n + C n 1 · 10 n — 1 · 1 + . . . + C n n — 2 · 10 2 · 10 n — 2 + C n n — 1 · 10 · 1 n — 1 + C n n · 1 n + + 20 n — 21 = = 10 n + C n 1 · 10 n — 1 · 1 + . . . + C n n — 2 · 10 2 · n · 10 + 1 + + 20 n — 21 = = 10 n + C n 1 · 10 n — 1 · 1 + . . . + C n n — 2 · 10 2 + 30 n — 20 = = 10 · 10 n — 1 + C n 1 · 10 n — 2 + . . . + C n n — 2 · 10 1 + 3 n — 2
Мы получили выражение, которое можно разделить на 10 ,поскольку там есть соответствующий множитель. Значение выражения в скобках будет представлять из себя натуральное число при любом натуральном значении n . Значит, исходное выражение 11 n + 20 n — 21 можно разделить на десять при любом натуральном n .
Ответ: данное выражение делится на 10 .
Еще один метод, который возможно применить в данном случае, – математическая индукция. Покажем на примере задачи, как это делается.
Условие: выясните, будет ли 11 n + 20 n — 21 делится на 10 при любом натуральном n .
Решение
Применим метод математической индукции. Если n будет равен единице, то у нас получится 11 n + 20 n — 21 = 11 1 + 20 · 1 — 21 = 10 . Деление десяти на десять возможно.
Допустим, что выражение 11 n + 20 n — 21 будет делиться на 10 при n = k , то есть 11 k + 20 k — 21 можно разделить на 10 .
Учитывая предположение, сделанное ранее, попробуем доказать, что выражение 11 n + 20 n — 21 делится на 10 при n = k + 1 . Для этого нам нужно преобразовать его следующим образом:
11 k + 1 + 20 · k + 1 — 21 = 11 · 11 k + 20 k — 1 = 11 · 11 k + 20 k — 21 — 200 k + 230 = = 11 · 11 k + 20 k — 21 — 10 · 20 k — 23
Выражение 11 · 11 k + 20 k — 21 в данной разности можно разделить на 10 , поскольку такое деление возможно и для 11 k + 20 k — 21 , а 10 · 20 k — 23 тоже делится на 10 , потому что это выражение содержит множитель 10 . Из этого мы можем заключить, что на 10 делится вся разность. Это и будет доказательством того, что 11 n + 20 n — 21 делится на 10 при любом натуральном значении n.
Если нам нужно проверить, делится ли на 10 многочлен с переменной n , допускается следующий подход: доказываем, что при n = 10 · m , n = 10 · m + 1 , … , n = 10 · m + 9 , где m – целое число, значение исходного выражения можно разделить на 10 . Это докажет нам делимость такого выражения при любом целом n . Несколько примеров доказательств, где используется такой способ, можно найти в статье о других случаях делимости на три.
Признаки делимости чисел
В данной публикации мы рассмотрим признаки делимости на числа от 2 до 11, сопроводив их примерами для лучшего понимания.
Признак делимости – это алгоритм, используя который можно сравнительно быстро определить, является ли рассматриваемое число кратным заранее заданному (т.е. делится ли на него без остатка).
- Признак делимости на 2
- Признак делимости на 3
- Признак делимости на 4
- Признак делимости на 5
- Признак делимости на 6
- Признак делимости на 7
- Признак делимости на 8
- Признак делимости на 9
- Признак делимости на 10
- Признак делимости на 11
Признак делимости на 2
Число делится на 2 тогда и только тогда, когда его последняя цифра является четной, т.е. также делится на два.
Примеры:
- 4, 32, 50, 112, 2174 – последние цифры этих чисел четные, значит они делятся на 2.
Признак делимости на 3
Число делится на 3 тогда и только тогда, когда сумма всех его цифр, также, делится на три.
Примеры:
- 18 – делится на 3, т.к. 1+8=9, а число 9 делится на 3 (9:3=3).
Признак делимости на 4
Двузначное число
Число делится на 4 тогда и только тогда, когда сумма удвоенной цифры в разряде его десятков и цифры в разряде единиц, также, делится на четыре.
- 64 – делится на 4, т.к. 6⋅2+4=16, а 16:4=4.
- 35 – не делится на 4, т.к. 3⋅2+5=11, а .
Число разрядов больше 2
Число кратно 4, когда две его последние цифры образуют число, делящееся на четыре.
- 344 – делится на 4, т.к. 44 кратно 4 (по алгоритму выше: 4⋅2+4=12, 12:4=3).
Примечание:
Число делится на 4 без остатка, если:
- в его последнем разряде стоят цифры 0, 4 или 8, а предпоследний разряд при этом является четным;
- в последнем разряде – 2 или 6, а в предпоследнем – нечетные цифры.
Признак делимости на 5
Число делится на 5 тогда и только тогда, когда его последняя цифра – это 0 или 5.
Примеры:
- 10, 65, 125, 300, 3480 – делятся на 5, т.к. оканчиваются на 0 или 5.
Признак делимости на 6
Число делится на 6 тогда и только тогда, когда он одновременно кратно и двум, и трем (см. признаки выше).
Примеры:
- 486 – делится на 6, т.к. делится на 2 (последняя цифра 6 – четная) и на 3 (4+8+6=18, 18:3=6).
- 712 – не делится на 6, т.к. оно кратно только 2.
- 1345 – не делится на 6, т.к. не является кратным ни 2, ни 3.
Признак делимости на 7
Число делится на 7 тогда и только тогда, когда сумма утроенного числа его десятков и цифры в разряде единиц, также, делится на семь.
- 91 – делится на 7, т.к. 9⋅3+1=28, а 28:7=4.
- 105 – делится на 7, т.к. 10⋅3+5=35, а 35:7=5 (в числе 105 – десять десятков).
- 812 – делится на 7. Здесь следующая цепочка: 81⋅3+2=245, 24⋅3+5=77, 7⋅3+7=28, а 28:7=4.
- 302 – не делится на 7, т.к. 30⋅3+2=92, 9⋅3+2=29, а число 29 на 7 не делится.
Признак делимости на 8
Трехзначное число
Число делится на 8 тогда и только тогда, когда сумма цифры в разряде единиц, удвоенной цифры в разряде десятков и учетверенной в разряде сотен делится на восемь.
- 264 – делится 8, т.к. 2⋅4+6⋅2+4=24, а 24:8=3.
- 716 – не делится 8, т.к. 7⋅4+1⋅2+6=36, а .
Число разрядов больше 3
Число делится на 8, когда три последние цифры образуют число, делящееся на 8.
- 2336 – делится на 8, т.к. 336 кратно 8.
- 12547 – не кратно 8, т.к. 547 не делится без остатка на восемь.
Признак делимости на 9
Число делится на 9 тогда и только тогда, когда сумма всех его цифр, также, делится на девять.
Примеры:
- 324 – делится на 9, т.к. 3+2+4=9, а 9:9=1.
- 921 – не делится на 9, т.к. 9+2+1=12, а
Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.
Примеры:
- 10, 110, 1500, 12760 – кратные 10 числа, последняя цифра – 0.
- 53, 117, 1254, 2763 – не делятся на 10.
Признак делимости на 11
Число делится на 11 тогда и только тогда, когда модуль разности сумм четных и нечетных разрядов равен нулю или делится на одиннадцать.
Rounding off numbers are discussed here, where we need to round a number. Rounding
can be done for every place value of a number.
(i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left.
(ii) If we purchase another thing and its cost is $15.78. The cost is rounded up to its nearest $16. 0.22 or 22¢ more is taken.
Similarly, any number is taken to its nearest convenient whole number. As 48 is nearer to 50 than 40, so 48 may be rounded up to 50. This is called rounding off the number. In the process of rounding of a number, it is taken to its closest whole number.
Rounding off a number makes it easier to estimate the answer in our daily life. It is also an easy way to check calculations mentally. Look at the number line below and observe how rounding of a number can be done using the number-line.
11 is closer to 10 than 20. Hence 11 is rounded down to 10.
28 is closer to 30 than 20. Hence 28 is rounded up to 30.
If the given number is between the two multiples of ten, it
is rounded up to the higher multiple. So 5 is rounded up to 10.
Note: To round off a number to the nearest tens, we round
off it to the nearest multiple of ten.
Consider the following examples:
Round off a Number to the Nearest Tens:
1. Round 78 to the nearest multiple of 10.
Solution:
To round off a number to the nearest tens, we round off it to the nearest multiple of ten.
78 is situated between 70 and 80. The middle of 70 and 80 is 75. 78 is nearer to 80 and farther from 70.
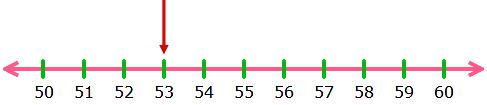
2. Round 53 to its nearest multiple of 10.
Solution:
53 is situated between 50 and 60. The middle number between 50 and 60 is 55.
53 is before 55, so it is rounded down to 50.
(When any number is situated half way or in the middle of two convenient
whole numbers, it is rounded up to the higher whole number)
55 is rounded up to 60, 75 is rounded up to 80
54 is rounded down to 50, 74 is rounded down to 70
3. 37 is
rounded up to 40 because 37 is closer to 40 than 30.
Round off a Number to the Nearest Hundreds:
To round
off a number to the nearest hundreds, we round off it to the nearest multiple
of hundred.
For Example:
225 is
nearer to 200 than 300. So, 225 is rounded down to 200.
Round off Number to the Nearest Thousands
To round
off number to the nearest thousands, we round off it to the nearest multiple of
thousand.
For example:
5431 is nearer
to 5000 than 6000. So, 5431 is rounded down to 5000.
Questions and Answers on Rounding off Numbers:
I. Round
off the following numbers to nearest tens:
(i) 39
(ii)
183
(iii) 102
(iv) 209
(v) 1268
(vi) 5186
(vii) 9549
(viii) 8911
Answers:
(i) 40
(ii) 180
(iii) 100
(iv) 210
(v) 127068
(vi) 5190
(vii) 9550
(viii) 8910
II. Round
off the following numbers to nearest hundreds:
(i) 3081
(ii) 5232
(iii) 4884
(iv) 6012
Answers:
(i) 3100
(ii) 5200
(iii) 4900
(iv) 6000
III. Round
off the following numbers to nearest thousands:
(i) 4128
(ii) 2854
(iii) 14585
(iv) 27102
Answers:
(i) 4000
(ii) 3000
(iii) 15000
(iv) 27000
IV. Using number line, round off following numbers to the
nearest tens:
(i) Round 72 to the nearest tens.
72 is closer to _______. Hence it is rounded down to
_______.
(ii) Round 39 to the nearest tens.
39 is closer to _______. Hence it is rounded down to
_______.
Answer:
IV. (i) 72 is closer to 70. Hence it is rounded down to 70.
(ii) 39 is closer to 40. Hence it is rounded up to 40.
V. Round the given numbers to the nearest tens:
(i) 42
(ii) 67
(iii) 89
(iv) 47
(v) 56
(vi) 78
Answer:
V. (i) 40
(ii) 70
(iii) 90
(iv) 50
(v) 60
(vi) 80
Related Concept
● Formation of Numbers.
● Finding Out the Numbers
● Names of the Numbers.
● Numbers Showing on Spike Abacus.
● 1 Digit Number on Spike Abacus.
● 2 Digits Number on Spike Abacus.
● 3 Digits Number on Spike Abacus.
● 4 Digits Number on Spike Abacus.
● 5 Digits Number on Spike Abacus.
● Large Number.
● Place Value Chart.
● Place Value.
● Problems Related to Place Value.
● Expanded form of a Number.
● Standard Form.
● Comparison of Numbers.
● Example on Comparison of Numbers.
● Successor and Predecessor of a Whole Number.
● Arranging Numbers.
● Formation of Numbers with the Given Digits.
● Formation of Greatest and Smallest Numbers.
● Examples on the Formation of Greatest and the Smallest Number.
● Rounding off Numbers.
4th Grade Math Worksheets
From Rounding off Numbers to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.