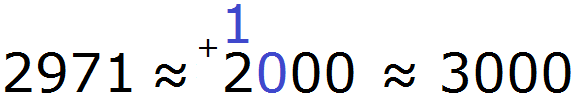Сегодня мы рассмотрим довольно скучную тему, без понимания которой двигаться дальше не представляется возможным. Эта тема называется «округление чисел» или по-другому «приближённые значения чисел».
Приближённые значения
Приближённые (или приблизительные) значения применяются тогда, когда точное значение чего-то найти невозможно, или же не важно чтобы это значение было точным для исследуемого предмета.
Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают. Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек.
Ещё пример. В девять утра начинаются занятия. Мы вышли из дома в 8:30. Через некоторое время по дороге мы встретили своего товарища, который спросил у нас сколько сейчас времени. Когда мы выходили из дома было 8:30, на дорогу мы потратили какое-то неизвестное время. Мы не знаем сколько сейчас времени, поэтому отвечаем товарищу: «сейчас приблизительно около девяти часов».
В математике приближенные значения указываются с помощью специального знака. Выглядит он следующим образом:
Читается как «приближённо (приблизительно) равно».
Чтобы указать приближённое (приблизительное) значение, прибегают к такому действию как округление чисел.
Округление чисел
Для нахождения приближенного значения применяется такое действие как округление чисел.
Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 100, 300, 700, 1000
Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.
Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.
На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.
Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).
Предстáвим числа от 10 до 20 с помощью следующего рисунка:
На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″
17 ≈ 20
Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.
Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:
На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10
12 ≈ 10
Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.
Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:
На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20
15 ≈ 20
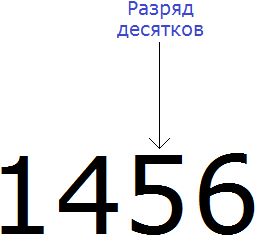
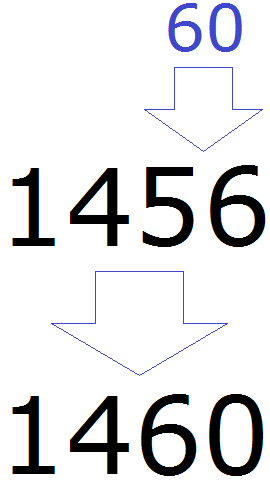
Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.
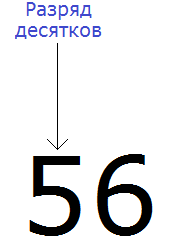
Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:
Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56
Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60
Значит при округлении числа 1456 до разряда десятков полýчим 1460
1456 ≈ 1460
Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.
Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.
После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.
Первое правило округления
В предыдущих примерах мы видели, что округляя число до определенного разряда, младшие разряды заменяются нулями. Цифры, которые заменяются нулями, называют отбрасываемыми цифрами.
Первое правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
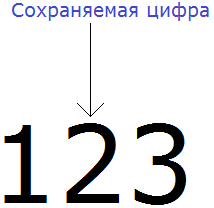
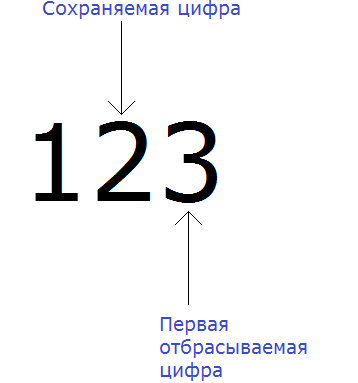
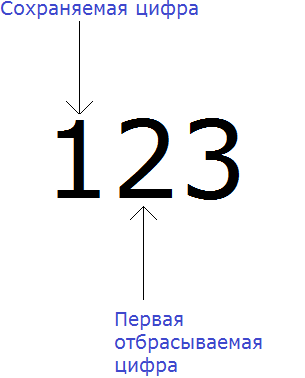
Например, округлим число 123 до разряда десятков.
В первую очередь находим сохраняемую цифру. Для этого надо прочитать самó задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 123 до разряда десятков.
Видим, что в разряде десятков нахóдится двойка. Значит сохраняемой цифрой является цифра 2
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после двойки это цифра 3. Значит цифра 3 является первой отбрасываемой цифрой.
Теперь применяем правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 2 заменяем нулями (точнее нулём):
123 ≈ 120
Значит при округлении числа 123 до разряда десятков, получаем приближённое ему число 120.
Теперь попробуем округлить то же самое число 123, но уже до разряда сотен.
Нам требуется округлить число 123 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 1, поскольку мы округляем число до разряда сотен.
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после единицы это цифра 2. Значит цифра 2 является первой отбрасываемой цифрой:
Теперь применим правило. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 1 заменяем нулями:
123 ≈ 100
Значит при округлении числа 123 до разряда сотен, получаем приближённое ему число 100.
Пример 3. Округлить число 1234 до разряда десятков.
Здесь сохраняемая цифра это 3. А первая отбрасываемая цифра это 4. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 3 без изменений, а всё что располагается после неё заменяем нулём:
1234 ≈ 1230
Пример 4. Округлить число 1234 до разряда сотен.
Здесь сохраняемая цифра это 2. А первая отбрасываемая цифра это 3. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 2 без изменений, а всё что располагается после неё заменяем нулями:
1234 ≈ 1200
Пример 3. Округлить число 1234 до разряда тысяч.
Здесь сохраняемая цифра это 1. А первая отбрасываемая цифра это 2. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 1 без изменений, а всё что располагается после неё заменяем нулями:
1234 ≈ 1000
Второе правило округления
Второе правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
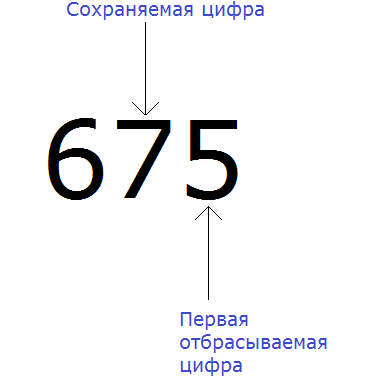
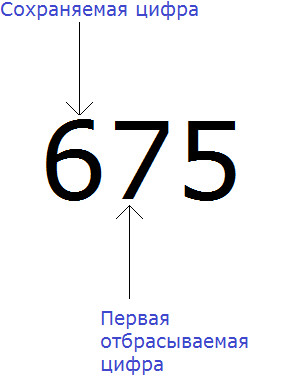
Например, округлим число 675 до разряда десятков.
В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 675 до разряда десятков.
Видим, что в разряде десятков находится семёрка. Значит сохраняемой цифрой является цифра 7
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой.
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 5. Значит мы должны увеличить на единицу сохраняемую цифру 7, а всё что следует после неё заменить нулём:
675 ≈ 680
Значит при округлении числа 675 до разряда десятков, получаем приближённое ему число 680.
Теперь попробуем округлить то же самое число 675, но уже до разряда сотен.
Нам требуется округлить число 675 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 6, поскольку мы округляем число до разряда сотен:
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после шестёрки это цифра 7. Значит цифра 7 является первой отбрасываемой цифрой:
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 7. Значит мы должны увеличить на единицу сохраняемую цифру 6, а всё что следует после неё заменить нулями:
675 ≈ 700
Значит при округлении числа 675 до разряда сотен, получаем приближённое ему число 700.
Пример 3. Округлить число 9876 до разряда десятков.
Здесь сохраняемая цифра это 7. А первая отбрасываемая цифра это 6. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 7, а всё что располагается после неё заменяем нулём:
9876 ≈ 9880
Пример 4. Округлить число 9876 до разряда сотен.
Здесь сохраняемая цифра это 8. А первая отбрасываемая цифра это 7. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 8, а всё что располагается после неё заменяем нулями:
9876 ≈ 9900
Пример 5. Округлить число 9876 до разряда тысяч.
Здесь сохраняемая цифра это 9. А первая отбрасываемая цифра это 8. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 9, а всё что располагается после неё заменяем нулями:
9876 ≈ 10000
Пример 6. Округлить число 2971 до сотен.
При округлении этого числа до сотен следует быть внимательным, поскольку сохраняемая цифра здесь 9, а первая отбрасываемая цифра это 7. Значит цифра 9 должна увеличиться на единицу. Но дело в том, что после увеличения девятки на единицу получится 10, а это цифра не вместится в разряд сотен нового числа.
В этом случае, в разряде сотен нового числа надо записать 0, а единицу перенести на следующий разряд и сложить с цифрой, которая там находится. Далее заменить все цифры после сохраняемой нулями:
2971 ≈ 3000
Округление десятичных дробей
При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:
Разряды целой части:
- разряд единиц;
- разряд десятков;
- разряд сотен;
- разряд тысяч.
Разряды дробной части:
- разряд десятых;
- разряд сотых;
- разряд тысячных
Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды. Очень важно не путать их:
Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.
Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков, а не разряда десятых. Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной.
Итак, мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):
123,456 ≈ 120
Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц. Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:
123,456 ≈ 123,0
Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:
123,456 ≈ 123,0 ≈ 123
Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,500
Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,460
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Округление чисел
- Правила округления
Числа, с которыми нам приходится иметь дело в реальной жизни, бывают двух типов. Одни в точности передают истинную величину, другие — только приблизительную. Первые называют точными, вторые — приближёнными.
В реальной жизни чаще всего пользуются приближёнными числами вместо точных, так как последние обычно не требуются. Например, приближённые значения используются при указании таких величин как длина или вес. Во многих же случаях точное число найти невозможно.
Правила округления
Для получения приближённого значения, полученное в результате каких-либо действий число нужно округлить, то есть заменить его ближайшим круглым
числом.
Числа всегда округляют до определённого разряда. Натуральные числа округляются до десятков, сотен, тысяч и т. д. При округлении чисел до десятков, их заменяют круглыми
числами, состоящими только из целых десятков, у таких чисел в разряде единиц стоят нули. При округлении до сотен, числа заменяются на более круглые
, состоящие только из целых сотен, то есть нули стоят уже и в разряде единиц, и в разряде десятков. И так далее.
Десятичные дроби можно округлять так же как и натуральные числа, то есть до десятков, сотен и т. д. Но также их можно округлять и до десятых, сотых, тысячных частей и т. д. При округлении десятичных знаков разряды не заполняются нулями, а просто отбрасываются. В обоих случаях округление производится по определённому правилу:
Если отбрасываемая цифра больше или равна 5, то предыдущую нужно увеличить на единицу, а если меньше 5, то предыдущая цифра не меняется.
Рассмотрим несколько примеров округления чисел:
- Округлить 43152 до тысяч. Здесь надо отбросить 152 единицы, так как справа от разряда тысяч стоит цифра 1, то предыдущую цифру отставляем без изменений. Приближённое значение числа 43152, округлённое до тысяч будет равно 43000.
- Округлить 43152 до сотен. Первая из отбрасываемых чисел 5, значит предыдущую цифру увеличиваем на единицу:
43152 ≈ 43200.
- Округлить 43152 до десятков:
43152 ≈ 43150.
- Округлить 17,7438 до единиц:
17,7438 ≈ 18.
- Округлить 17,7438 до десятых:
17,7438 ≈ 17,7.
- Округлить 17,7438 до сотых:
17,7438 ≈ 17,74.
- Округлить 17,7438 до тысячных:
17,7438 ≈ 17,744.
Знак ≈
называют знаком приближённого равенства, он читается — приближённо равно
.
Если при округлении числа результат получился больше начального значения, то полученное значение называется приближённым значением с избытком, если меньше — приближённым значением с недостатком:
7928 ≈ 8000,
число 8000 — приближённое значением с избытком,
5102 ≈ 5000,
число 5000 — приближённое значением с недостатком.
Человеку постоянно приходится сталкиваться с решением различных практических и теоретических задач, которые чаще всего связаны с нахождением числовых значений величин.
Измерить какую-либо величину- это значит сравнить ее с однородной величиной, принятой за единицу измерения.
В большинстве случаев полученные значения в результате вычислений и измерений получаются неточными, приближенными: немного больше или меньше истинного значения.
Точность- это степень приближения результата измерения (вычисления) к реальному значению.
Чем меньше точность, тем больше погрешность (расхождение истинного и полученного значения) и, соответственно, чем меньше погрешность, тем выше точность.
Точные измерения проблематичны в реальности по ряду причин:
Эта информация доступна зарегистрированным пользователям
- Несовершенство органов чувств человека.
- Неточность и несовершенство измерительных приборов.
- Характеристики самого измеряемого объекта, не позволяющие выполнить точные измерения и вычисления.
Так, например, невозможно точно до метра определить протяженность рек, гор, расстояние от Земли до Луны, с точностью до грамма проблематично определить массу грузовика и т.д.
Сегодня на уроке мы научимся находить приближенные значения с избытком и недостатком.
Эта информация доступна зарегистрированным пользователям
Познакомимся с правилом округления чисел до заданного разряда.
Рассмотрим несколько примеров округления чисел.
В настоящее время в различные сферы жизни человека все больше внедряются современные высокоточные устройства, которые позволяют быстро и точно производить измерения и вычисления.
Однако, порой нам даже нет необходимости знать точное значение величины.
Не раз нам приходилось встречать такие фразы: «около одного часа», «примерно один килограмм» или «приблизительно двадцать тысяч рублей» и т.п.
В подобных фразах синонимы: «около», «примерно», «приблизительно» и т.д. указывают на приближенность значений величины, на чуть большее или меньшее значение относительно реального.
Например, говоря о своем возрасте, мы чаще всего называем количество лет и месяцев, не упоминая о прожитых днях и часах.
На вопрос «который час?» мы скорее всего назовем сколько часов и минут в данный промежуток времени, не указывая секунды.
Числа, с которыми нам приходится встречаться и использовать в действительности, бывают двух типов:
- Точные (в истинности которых мы не сомневаемся).
Например, говоря о том, что у треугольника 3 стороны, число 3 представляет собой точным числом.
Эта информация доступна зарегистрированным пользователям
В утверждении о том, что стул имеет 4 ножки, число 4 так же является точным.
Эта информация доступна зарегистрированным пользователям
- Приближенные (близкие к истинному значению).
На практике, измеряя расстояние, массу, температуру, объем, площадь и другие величины, мы не можем определить их точные значения, а порой эти точные значения вовсе не требуется находить.
Эта информация доступна зарегистрированным пользователям
Поэтому важно знать (заранее установить) с какой точностью необходимо выполнить измерения и вычисления, т.е. необходимо выяснить какие доли единицы измерения необходимо принять во внимание, а какими можно пренебречь.
Приближенные значения делят на:
- Приближенные значения с недостатком.
- Приближенные значения с избытком.
Рассмотрим поясняющий пример.
Обратите внимание на рисунок.
Эта информация доступна зарегистрированным пользователям
Улитка проползла некоторое расстояние и остановилась, данное расстояние обозначим как х (см).
Заметим, что улитка смогла преодолеть больше 7 см, но не смогла доползти до отметки 8 см.
Получается, что расстояние, которое проползла улитка больше 7 см, но меньше 8 см:
7 < x < 8
В данном случае число 7, 8– это приближенные значения числа х.
Путь, который проползла улитка, изображен в виде отрезка МN.
Конец отрезка MN заключен между отметками 7 см и 8 см.
Если А< x < В (число х больше числа А, но меньше числа В), то А называют приближенным значением числа х с недостатком, а число В– приближенным значением числа х с избытком.
Получаем в нашем случае 7 см- это приближенное значение длины отрезка MN с недостатком, а 8 см- это приближенное значение длины отрезка MN с избытком.
Так, если бы улитка проползла х = 6,3 см, то 6 см являлось бы приближенным значением пути улитки с недостатком, а значение 7 см было бы приближенным значением пути с избытком.
Рассмотрим пару заданий, в которых необходимо произвести оценку величины.
Задание №1.
Из предложенных чисел 2,1; 2,7; 4,1; 3,2; 2,4; 3,5 выберите те, для которых 2,3 является приближенным значением числа с недостатком, а число 3,7 является приближенным значением числа с избытком.
Для искомых чисел должно выполняться условие 2,3 < x < 3,7.
Такому условию удовлетворяют следующие десятичные дроби:
2,4 так как 2,3 < 2,4 < 3,7
2,7 так как 2,3 < 2,7 < 3,7
3,2 так как 2,3 < 3,2 < 3,7
3,5 так как 2,3 < 3,5 < 3,7
Задание №2.
Определите между какими двумя ближайшими натуральными числами расположена дробь 2,4.
К какому натуральному числу ближе заданная десятичная дробь 2,4?
С помощью координатного луча мы можем оценить расположение десятичной дроби.
Отметим на координатном луче число 2,4 (две целых четыре десятых).
Разложим заданное число по разрядам.
2,4 = 2 + 0,4
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Эта информация доступна зарегистрированным пользователям
Отложим два целых единичных отрезка от начала координат, получим две целых единицы.
Чтобы отметить дробь 0,4, третий единичный отрезок разделим на десять долей, каждая такая доля будет равна (mathbf{frac{1}{10} = 0,1}).
От точки с координатой 2 отложим вправо четыре доли единичного отрезка ОЕ, получим точку 2,4.
Если мы посмотрим на координатный луч, то заметим, что десятичная дробь 2,4 находится между натуральными числами 2 и 3, причем десятичная дробь 2,4 удалена от точки 2 всего на четыре доли единичного отрезка, а точка 3 удалена от точки 2,4 на шесть таких долей, следовательно, десятичная дробь 2,4 расположена ближе к натуральному числу 2.
2 < 2,4 < 3
Эта информация доступна зарегистрированным пользователям
Чтобы найти приближенное значение числа, используют математическое действие- округление чисел (замена числа его ближайшим «круглым» числом).
«Круглым» числом называют число, оканчивающееся одним или несколькими нулями.
Округление- это математическая операция, с помощью которой можно уменьшить количество знаков в числе за счет замены этого числа его близким значением с определенной точностью.
Суть операции округления заключается в нахождении числа ближайшего по своему значению к истинному.
Округлить можно любое число до любого разряда.
Важно знать и помнить правильное название и расположение разрядов в числе.
Вспомним разряды десятичных дробей.
Эта информация доступна зарегистрированным пользователям
Замену числа ближайшим к нему натуральным числом или нулем называют округлением этого числа до целых.
Десятичные дроби возможно округлять так же как натуральные числа до единиц, десятков, сотен, тысяч и т.д.
При округлении числа до десятков число заменяют «круглым» числом, которое должно состоять из целых десятков, а вместо разряда единиц должен быть нуль.
Если необходимо округлить число, например, до сотен, это число заменяют «круглым» числом, в котором остается разряд сотен, а в разряде десятков и единиц должны стоять нули.
Пример.
Округлим 1,7 до целого.
Рассмотрим процесс округления десятичной дроби с помощью координатного луча.
Разложим заданное число по разрядам.
1,7 = 1 + 0,7
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Эта информация доступна зарегистрированным пользователям
Отметим на координатном луче точку с координатой 1,7.
Отложим один целый единичный отрезок от начала координат, получим одну целую единицу.
Чтобы отметить дробь 0,7, второй единичный отрезок разделим на десять долей, каждая такая доля будет равна (mathbf{frac{1}{10} = 0,1}).
От точки с координатой 1 отложим вправо семь долей единичного отрезка ОЕ, получим точку с координатой 1,7.
Обратим внимание, что точка 1,7 находится между натуральными числами 1 и 2.
Точка с координатой 1,7 удалена от точки Е(1) на семь долей единичного отрезка ОЕ, а от точки с координатой 2– всего на три доли единичного отрезка ОЕ.
Таким образом, можно утверждать, что точка с координатой 1,7 расположена ближе к точке с координатой 2.
Значит, при округлении числа 1,7 до целых получается число 2 (1,7 приближенно равно 2).
1,7 ≈ 2
Десятичные дроби так же можно округлять до определенного разряда, стоящего после десятичной запятой: до десятых, сотых, тысячных и т.д.
При округлении до какого-либо разряда все последующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их просто отбрасывают.
Округление чисел происходит по определенному правилу, рассмотрим его.
Чтобы округлить число до какого-либо разряда нужно:
Эта информация доступна зарегистрированным пользователям
Поясним на примерах.
Пример №1.
Округлим 83421 до сотен.
Решение:
Подчеркнем в числе цифру 4, так как она стоит в разряде сотен.
83421
За подчеркнутой цифрой стоит цифра 2, следовательно, необходимо действовать согласно Правила №1: оставить цифру 4 без изменения.
Все цифры, стоящие после разряда сотен (цифры 2 и 1), заменим нулями.
Эта информация доступна зарегистрированным пользователям
В итоге получим округление числа 83421 до 83400.
Результат запишем следующим образом: 83421 ≈ 83400.
Пример №2.
Округлим до разряда единиц число 316,52.
Решение:
Число 316,52 будем округлять до целых.
Известно, что десятичная дробь состоит из целой части (находящейся до десятичной запятой) и дробной части (находящейся после десятичной запятой).
В заданной десятичной дроби 316,52 в разряде единиц стоит цифра 6.
Подчеркнем цифру 6.
316,52
Цифра, стоящая справа от подчеркнутой цифры- это цифра 5, следовательно, необходимо действовать согласно Правила №2: к подчеркнутой цифре 6 прибавить единицу.
Получим в разряде единиц цифру 7, все цифры, стоящие следом за округляемым разрядом (стоящие после десятичной запятой), отбрасываем.
Эта информация доступна зарегистрированным пользователям
В итоге получим округление числа 316,52 до 317.
Результат запишем следующим образом: 316,52 ≈ 317.
Пример №2.
Округлим число 27,819 до разряда сотых.
Решение:
В заданной десятичной дроби 27,819 в разряде сотых стоит цифра 1, подчеркнем ее.
27,819
За подчеркнутым разрядом стоит цифра 9, следовательно, необходимо действовать согласно Правила №2: к подчеркнутой цифре 1 прибавить единицу.
Получим в разряде сотых цифру 2, все цифры, следующие за разрядом сотых, просто отбрасываем.
Эта информация доступна зарегистрированным пользователям
В итоге получим округление числа 27,819 до 27,82.
Результат запишем следующим образом: 27,819 ≈ 27,82.
Эта информация доступна зарегистрированным пользователям
Рассмотрим несколько примеров округления чисел при решении задач.
Задача №1.
Эта информация доступна зарегистрированным пользователям
В первый день продали 20,35 м ткани, во второй день еще 17,8 м ткани.
Сколько метров ткани продали за два дня?
Ответ округлите до десятых.
Решение:
Кратко запишем условие задачи.
Эта информация доступна зарегистрированным пользователям
Схематично изобразим условие задачи.
Эта информация доступна зарегистрированным пользователям
Сложим ткань, которую продали в первый и во второй день, в результате получим сколько метров ткани продали за два дня.
Эта информация доступна зарегистрированным пользователям
20,35 + 17,8 = 38,15 (м) ткани продали за два дня.
Округлим полученное число 38,15 до десятых.
В полученной десятичной дроби 38,15 в разряде десятых стоит цифра 1, подчеркнем ее.
38,15
За подчеркнутым разрядом стоит цифра 5, следовательно, необходимо действовать согласно Правила №2: к подчеркнутой цифре 1 прибавить единицу.
Получим в разряде десятых цифру 2, все цифры, следующие за подчеркнутой цифрой, просто отбрасываем.
Результат запишем следующим образом: 38,15 ≈ 38,2.
Ответ: 38,2 (м).
Задача №2.
Эта информация доступна зарегистрированным пользователям
В первый день автомобиль проехал 124,4 км, а во второй день на 31,2 км меньше.
Какой путь проехал автомобиль за эти два дня?
Ответ округлите до целых.
Решение:
Кратко запишем условие задачи.
Проехал в первый день- 124,4 км
Проехал во второй день- 124,4 – 31,2 км
Чтобы найти путь, который проехал автомобиль, необходимо сложить пройденный путь в первый и во второй день.
Составим выражение.
124,4 + (124,4 – 31,2)
Найдем значение полученного выражения.
Выражение содержит несколько арифметических операций и скобки.
1. Выполним действия в скобках (найдем разность двух десятичных дробей).
Эта информация доступна зарегистрированным пользователям
2. Сложим полученный результат и 124,4.
Эта информация доступна зарегистрированным пользователям
124,4 + 93,2 = 217,6 (км) автомобиль проехал за два дня.
Округлим полученный результат до целых.
В полученной десятичной дроби 217,6 в разряде единиц (в самом младшем разряде целой части десятичной дроби) стоит цифра 7, подчеркнем ее.
217,6
После подчеркнутой цифры стоит цифра 6, следовательно, чтобы верно округлить число, необходимо действовать согласно Правила №2: к подчеркнутой цифре 7 нужно прибавить единицу.
Получим в разряде единиц цифру 8, все цифры, следующие за подчеркнутой цифрой, просто отбрасываем.
Результат запишем следующим образом: 217,6 ≈ 218.
Ответ: 218 (км).
Задача №3.
Эта информация доступна зарегистрированным пользователям
За два дня было продано 45,35 (кг) конфет. В первый день продали 31,20 (кг).
На сколько больше конфет продали в первый день, чем во второй?
Ответ округлите до десятых.
Решение:
Кратко запишем условие задачи.
Эта информация доступна зарегистрированным пользователям
Первым действием найдем сколько конфет продали во второй день, для этого вычтем конфеты, проданные в первый день из общего количества конфет, проданных за два дня.
Эта информация доступна зарегистрированным пользователям
1. 45,35 – 31,20 = 14,15 (кг) конфет продали во второй день.
Следующим действием найдем на сколько килограммов конфет было продано больше в первый день, чем во второй.
Эта информация доступна зарегистрированным пользователям
2. 31,20 – 14,15 = 17,05 (кг)
Округлим полученный результат (десятичную дробь 17,05) до десятых.
В полученной десятичной дроби 17,05 в разряде десятых стоит цифра 0, подчеркнем ее.
17,05
За подчеркнутым разрядом стоит цифра 5, следовательно, необходимо действовать согласно Правила №2: к подчеркнутой цифре 0 прибавить единицу.
Получим в разряде десятых цифру 1, все цифры, следующие за подчеркнутой цифрой, просто отбрасываем.
Результат запишем следующим образом: 17,05 ≈ 17,1.
Ответ: в первый день продали на 17,1 кг конфет больше, чем во второй день.
Эта информация доступна зарегистрированным пользователям
Читайте также
Под каждым числом в таблице запиши ближайшее к нему число круглых сотен.
289, 305, 893, 917, 999, 401, 500, 152, 10.
Вы находитесь на странице вопроса Под каждым числом в таблице запиши ближайшее к нему число круглых сотен? из категории Математика.
Уровень сложности вопроса рассчитан на учащихся 1 – 4 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.
Приближённые (или приблизительные) значения применяются тогда, когда точное значение чего-либо найти невозможно, или же это значение не важно для исследуемого предмета.
Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают. Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек.
В математике приближенные значения указываются с помощью специального знака. Выглядит он следующим образом – ≈
И читается как «приблизительно равно». Чтобы указать приблизительное значение чего-либо, прибегают к такой операции, как округление чисел.
Округление чисел
Для нахождения приближенного значения применяется такая операция, как округление чисел. Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулем. Например, следующие числа являются круглыми – 10, 20, 30, 100, 300, 700, 1000
Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числа. Суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.
Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, от нас требуют найти ближайшее круглое число для числа 17. При этом, в ходе этого поиска возможно изменения коснутся и цифры, которая находится в разряде десятков в числе 17 (т.е единицы).
Представим, что все числа от 10 до 20 лежат на прямой линии. Понятно, что для числа 17 ближайшее круглое число это 20. Значит ответ к задаче таким и будет: 17 приблизительно равно 20
17 ≈ 20
Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.
Попробуем найти приближённое число для числа 12. Для этого снова представим, что все числа от 10 до 20 лежат на прямой линии. Ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приблизительно равно 10
12 ≈ 10
Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления.
Попробуем найти ближайшее число для числа 15. Снова представим, что все числа от 10 до 20 лежат на прямой линии. Число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать большее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20
15 ≈ 20
Округлять можно и большие числа. Естественно, для них рисовать прямую линию и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков. Разряд десятков начинается на пятёрке. Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56. Смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60. Значит при округлении числа 1456 до разряда десятков получим 1460
1456 ≈ 1460
Округлять числа можно не только до разряда десятков. Округлять можно также до разряда сотен, тысяч, десятков тысяч.
Становится понятно, что округление это ни что иное, как поиск ближайшего числа.