Как найти ближайшую прямую - Сайт, где вы сможете решить свои вопросы

Расстояние от точки до прямой на плоскости — это кратчайшее расстояние от точки до прямой в евклидовой геометрии. Расстояние равно длине отрезка, который соединяет точку с прямой и перпендикулярен прямой. Формула вычисления расстояния может быть получена и выражена несколькими способами.

Знание наименьшего расстояния от точки до прямой может быть полезно во многих случаях, например, для поиска кратчайшего пути для выхода на дорогу, определение разброса графа, и подобное. В регрессии Деминга, процедуре линейного сглаживания, если зависимые и независимые переменные имеют одну и ту же дисперсию, регрессия сводится к ортогональной регрессии, в которой степень приближения измеряется для каждой точки как расстояние от точки до регрессионной прямой.

Декартова система координат[править | править код]

Прямая задана уравнением[править | править код]

Когда прямая на плоскости задана уравнением ax + by + c = 0, где a, b и c — такие вещественные константы, что a и b не равны нулю одновременно, и расстояние от прямой до точки (x₀,y₀) равно ^[1]

${displaystyle operatorname {distance} (ax+by+c=0,(x_{0},y_{0}))={frac {|ax_{0}+by_{0}+c|}{sqrt {a^{2}+b^{2}}}}.}$

Точка на прямой, наиболее близкая к (x₀,y₀), имеет координаты ^[2]

${displaystyle x={frac {b(bx_{0}-ay_{0})-ac}{a^{2}+b^{2}}}}$

и ${displaystyle y={frac {a(-bx_{0}+ay_{0})-bc}{a^{2}+b^{2}}}.}$

Горизонтальные и вертикальные прямые

В общем уравнении прямой ax + by + c = 0 коэффициенты a и b не могут быть одновременно равны нулю пока c ненулевое, а в случае всех нулевых коэффициентов уравнение не задаёт прямую. Если a = 0, а b ≠ 0, прямая горизонтальна и имеет уравнение y = –c/b. Расстояние от (x₀, y₀) до этой прямой определяется вертикальным отрезком длины |y₀ — (-c/b)| = |by₀ + c| / |b| (согласно формуле). Аналогичным образом, для вертикальных прямых (b = 0) расстояние между той же точкой и прямой равно |ax₀ + c| / |a| и измеряется вдоль горизонтального отрезка.

Нормированное уравнение прямой

Нормированное уравнение прямой — это уравнение вида

{displaystyle xcos alpha +ysin alpha -p=0}

Нормированное уравнение получается из общего уравнения прямой ax + by + c = 0 делением всех членов на ${displaystyle {sqrt {a^{2}+b^{2}}}}$ .
Тогда расстояние от точки (x₀, y₀) до прямой равно абсолютному значению отклонения и вычисляется по формуле ^[3]^[4]

${displaystyle |d|=|x_{0}cos alpha +y_{0}sin alpha -p|}$

Прямая задана двумя точками[править | править код]

Если прямая проходит через две точки P₁=(x₁,y₁) и P₂=(x₂,y₂), и необходимо найти расстояние от ${displaystyle M=(x_{0},y_{0})}$ до прямой, то можно воспользоваться следующими способами:

Способ 1. Искомое расстояние равно

${displaystyle operatorname {distance} (P_{1},P_{2},(x_{0},y_{0}))={frac {|(y_{2}-y_{1})x_{0}-(x_{2}-x_{1})y_{0}+x_{2}y_{1}-y_{2}x_{1}|}{sqrt {(y_{2}-y_{1})^{2}+(x_{2}-x_{1})^{2}}}}.}$

Знаменатель этого выражения равен расстоянию между точками P₁ и P₂. Числитель равен удвоенной площади треугольника с вершинами (x₀,y₀), P₁ и P₂ (см. Общая формула площади треугольника в декартовых координатах). Выражение эквивалентно ${textstyle h={frac {2A}{b}}}$ , что может быть получено преобразованием стандартной формулы площади треугольника: ${textstyle A={frac {1}{2}}bh}$ , где b — длина стороны, а h — высота на эту сторону из противолежащей вершины.

Способ 2. Сначала находится ближайшая точка на прямой к точке по формуле

${displaystyle M_{p}=P_{1}+{overrightarrow {P_{1}P_{2}}}*{({overrightarrow {P_{1}P_{2}}},{overrightarrow {P_{1}M}}) over lVert {overrightarrow {P_{1}P_{2}}}rVert ^{2}}}$ .

Тогда искомое расстояние равно

${displaystyle operatorname {distance} (P_{1},P_{2},M)=lVert {overrightarrow {MM_{p}}}rVert }$ .

Доказательства[править | править код]

Алгебраическое доказательство[править | править код]

Это доказательство верно, только когда прямая не является ни вертикальной, ни горизонтальной. То есть мы предполагаем, что ни a, ни b в уравнении не равны нулю.

Прямая с уравнением ax + by + c = 0 имеет наклон –a/b, так что любая прямая, перпендикулярная к заданной, имеет наклон b/a. Пусть (m, n) — точка пересечения прямой ax + by + c = 0 и перпендикулярной прямой, проходящей через точку (x₀, y₀). Прямая, проходящая через эти две точки, перпендикулярна исходной прямой, так что

${displaystyle {frac {y_{0}-n}{x_{0}-m}}={frac {b}{a}}.}$

Таким образом,
${displaystyle a(y_{0}-n)-b(x_{0}-m)=0,}$
и после возведения в квадрат получим:

${displaystyle a^{2}(y_{0}-n)^{2}+b^{2}(x_{0}-m)^{2}-2ab(y_{0}-n)(x_{0}-m)=0.}$

Рассмотрим,

${displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=a^{2}(x_{0}-m)^{2}+2ab(y_{0}-n)(x_{0}-m)+b^{2}(y_{0}-n)^{2}=(a^{2}+b^{2})((x_{0}-m)^{2}+(y_{0}-n)^{2})}$

Здесь использовано возведённое в квадрат выражение. Но

${displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=(ax_{0}+by_{0}-am-bn)^{2}=(ax_{0}+by_{0}+c)^{2}}$

так как точка (m, n) расположена на прямой ax + by + c = 0.
Таким образом,

${displaystyle (a^{2}+b^{2})((x_{0}-m)^{2}+(y_{0}-n)^{2})=(ax_{0}+by_{0}+c)^{2}}$

Из этого получаем длину отрезка между этими двумя точками:

${displaystyle d={sqrt {(x_{0}-m)^{2}+(y_{0}-n)^{2}}}={frac {|ax_{0}+by_{0}+c|}{sqrt {a^{2}+b^{2}}}}.}$

^[5].

Геометрическое доказательство[править | править код]

Это доказательство верно, только когда прямая не является ни вертикальной, ни горизонтальной. Баллантин и Джерберт^[6] не упомянули это ограничение в своей статье.

Опустим перпендикуляр из точки P с координатами (x₀, y₀) на прямую с уравнением Ax + By + C = 0. Обозначим основание перпендикуляра буквой R. Проведём вертикальную прямую через P и обозначим пересечение этой вертикальной прямой с исходной прямой буквой S. В произвольной точке T на прямой нарисуем прямоугольный треугольник TVU, катеты которого являются горизонтальными и вертикальными отрезками, а длина горизонтального отрезка равна |B| (см. рисунок). Вертикальный катет треугольника ∆TVU будет иметь длину |A|, поскольку наклон прямой равен –A/B.

Треугольники ∆SRP и ∆UVT подобны, так как они оба прямоугольные и ∠PSR ≅ ∠VUT, поскольку являются соответственными углами двух параллельных прямых PS и UV (вертикальные прямые) и секущей (исходная прямая)^[7]. Выпишем отношения сторон этих треугольников:

${displaystyle {frac {|{overline {PR}}|}{|{overline {PS}}|}}={frac {|{overline {TV}}|}{|{overline {TU}}|}}.}$

Если точка S имеет координаты (x₀,m), то |PS| = |y₀ — m| и расстояние от P до прямой равно:

${displaystyle |{overline {PR}}|={frac {|y_{0}-m||B|}{sqrt {A^{2}+B^{2}}}}.}$

Поскольку S находится на прямой, мы можем найти значение m,

${displaystyle m={frac {-Ax_{0}-C}{B}},}$

и получаем: ^[6]

${displaystyle |{overline {PR}}|={frac {|Ax_{0}+By_{0}+C|}{sqrt {A^{2}+B^{2}}}}.}$

Другой вариант этого доказательства — поместить точку V в точку P и вычислить площадь треугольника ∆UVT двумя способами, после чего получим ,
где D — высота треугольника ∆UVT на гипотенузу из точки P. Формула расстояния может быть использована, чтобы выразить , и в терминах координат P и коэффициентов уравнения исходной прямой, в результате чего получим требуемую формулу.

Доказательство с помощью проекции вектора[править | править код]

Пусть P — точка с координатами (x₀, y₀) и пусть исходная прямая имеет уравнение ax + by + c = 0. Пусть Q = (x₁, y₁) — любая точка на прямой и n — вектор (a, b) с началом в точке Q. Вектор n перпендикулярен прямой, и расстояние d от точки P до прямой равно длине ортогональной проекции на n. Длина этой проекции равна:

${displaystyle d={frac {|{overrightarrow {QP}}cdot mathbf {n} |}{|mathbf {n} |}}.}$

Теперь

${displaystyle {overrightarrow {QP}}=(x_{0}-x_{1},y_{0}-y_{1}),}$

так что ${displaystyle {overrightarrow {QP}}cdot mathbf {n} =a(x_{0}-x_{1})+b(y_{0}-y_{1})}$

и ${displaystyle |mathbf {n} |={sqrt {a^{2}+b^{2}}}.}$

Тогда

${displaystyle d={frac {|a(x_{0}-x_{1})+b(y_{0}-y_{1})|}{sqrt {a^{2}+b^{2}}}}.}$

Поскольку Q лежит на прямой, ${displaystyle c=-ax_{1}-by_{1}}$ , а тогда ^[8]^[9]^[10]

${displaystyle d={frac {|ax_{0}+by_{0}+c|}{sqrt {a^{2}+b^{2}}}}.}$

Другие формулы[править | править код]

Можно получить другие выражения для кратчайшего расстояния от точки до прямой. Эти выводы тоже требуют, чтобы прямая не была вертикальной или горизонтальной.

Пусть точка P задана координатами ( ${displaystyle x_{0},y_{0}}$ ).
Пусть прямая задана уравнением y=mx+k . Уравнение прямой, перпендикулярной исходной прямой и проходящей через точку P, задаётся уравнением ${displaystyle y={frac {x_{0}-x}{m}}+y_{0}}$ .

Точка, в которой эти две прямые пересекаются, является ближайшей точкой на исходной прямой для точки P. Тогда:

${displaystyle mx+k={frac {x_{0}-x}{m}}+y_{0}.}$

Мы можем решить это уравнение по x,

${displaystyle x={frac {x_{0}+my_{0}-mk}{m^{2}+1}}.}$

Координату y точки пересечения можно найти, подставив значение x в уравнение исходной прямой,

${displaystyle y=m{frac {(x_{0}+my_{0}-mk)}{m^{2}+1}}+k.}$

Подставив полученные значения в формулу расстояния ${displaystyle d={sqrt {(X_{2}-X_{1})^{2}+(Y_{2}-Y_{1})^{2}}}}$ , получим формулу кратчайшего расстояния от точки до прямой:

${displaystyle d={sqrt {left({{frac {x_{0}+my_{0}-mk}{m^{2}+1}}-x_{0}}right)^{2}+left({m{frac {x_{0}+my_{0}-mk}{m^{2}+1}}+k-y_{0}}right)^{2}}}.}$

Если заметить, что m = –a/b и k = –c/b для уравнения ax + by + c = 0, после небольших выкладок получим стандартное выражение^[2].

Формулировка с помощью векторов[править | править код]

Иллюстрация формулировки с помощью векторов.

Запишем прямую в векторном виде:

{displaystyle mathbf {x} =mathbf {a} +tmathbf {n} }

где x — вектор, задающий координаты любой точки на прямой, n — единичный вектор в направлении прямой, a — вектор, задающий две координаты точки на прямой, а t — скаляр. То есть для получения точки x на прямой начинаем с точки a на прямой и двигаемся на расстояние t вдоль прямой.

Расстояние от произвольной точки p до прямой задаётся формулой

{displaystyle operatorname {distance} (mathbf {x} =mathbf {a} +tmathbf {n} ,mathbf {p} )=|(mathbf {a} -mathbf {p} )-((mathbf {a} -mathbf {p} )cdot mathbf {n} )mathbf {n} |.}

Эта формула геометрически строится следующим образом: — это вектор из p в точку a на прямой. Тогда — это длина проекции на прямую, а тогда

{displaystyle ((mathbf {a} -mathbf {p} )cdot mathbf {n} )mathbf {n} }

— это вектор, являющийся проекцией на прямую. Тогда

{displaystyle (mathbf {a} -mathbf {p} )-((mathbf {a} -mathbf {p} )cdot mathbf {n} )mathbf {n} }

является компонентой вектора , перпендикулярной прямой. Следовательно, расстояние от точки до прямой равно норме этого вектора^[11]. Эта формула может быть использована и в более высоких размерностях.

Другая формулировка с помощью векторов[править | править код]

Если векторное пространство ортонормально, а прямая (d ) проходит через точку B и имеет вектор направления^[en] vec u , то расстояние от точки A до прямой (d) равно

${displaystyle d(mathrm {A} ,(d))={frac {left|{overrightarrow {mathrm {BA} }}wedge {vec {u}}right|}{|{vec {u}}|}}}$

где — векторное произведение векторов и vec u , а — норма вектора vec u .

Обобщения[править | править код]

Расстояние от точки в трёхмерном пространстве до плоскости задаётся аналогичной формулой^[12]:

${displaystyle operatorname {distance} (ax+by+cz+d=0,(x_{0},y_{0},z_{0}))={frac {|ax_{0}+by_{0}+cz_{0}+d|}{sqrt {a^{2}+b^{2}+c^{2}}}}.}$

См. также[править | править код]

Пересечение двух прямых^[en]
Расстояние между двумя прямыми
Расстояние между скрещивающимися прямыми

Примечания[править | править код]

↑ Larson, Hostetler, 2007, p. 452.
↑ ¹ ² Larson, Hostetler, 2007, p. 522.
↑ Привалов, 1966, с. 67.
↑ Делоне, Райков, 1948, с. 195.
↑ Laudanski, 2014.
↑ ¹ ² Ballantine, Jerbert, 1952, с. 242–243.
↑ Если два треугольника окажутся по разные стороны от исходной прямой, эти углы будут накрест лежащими, а потому опять равными.
↑ Anton, 1994, с. 138-9.
↑ Федотов, Карпов, 2005, с. 86.
↑ Моденов, 1967, с. 152.
↑ Sunday, Dan. Lines and Distance of a Point to a Line. // softSurfer. Дата обращения: 6 декабря 2013. Архивировано 14 декабря 2017 года.
↑ OnlineMSchool. Дата обращения: 2 декабря 2020. Архивировано 17 января 2021 года.

Литература[править | править код]

Делоне Б. Н., Райков Д. А. . Аналитическая геометрия. T. 1. — М., Л.: ОГИЗ, 1948. — 456 с.
Моденов П. С. . Аналитическая геометрия. — М.: Изд-во Моск. ун-та, 1967. — 697 с.
Привалов И. И. . Аналитическая геометрия. 13-е изд. — М.: Наука, 1966. — 272 с.
Федотов А. Г., Карпов Б. В. . Аналитическая геометрия. — М.: МГИЭМ, 2005. — 158 с. — ISBN 5-94506-116-6.
Anton H. . Elementary Linear Algebra. 7th ed. — Somerset: John Wiley & Sons, 1994. — ISBN 0-471-58742-7.
Ballantine J. P., Jerbert A. R. Distance from a Line or Plane to a Point // American Mathematical Monthly. — 1952. — Vol. 59. — P. 242—243. — doi:10.2307/2306514.
Larson R., Hostetler R. . Precalculus: A Concise Course. — Boston: Houghton Mifflin, 2007. — xvii + 526 + 102 p. — ISBN 0-618-62719-7.
Laudański L. M. . Between Certainty and Uncertainty: Statistics and Probability in Five Units with Notes on Historical Origins and Illustrative Numerical Examples. — Berlin; Heidelberg: Springer Verlag, 2014. — x + 318 p. — (Intelligent Systems Reference Library, vol. 31). — ISBN 978-3-642-25696-7.

Дополнительная литература[править | править код]

Deza M. M., Deza E. . Encyclopedia of Distances. 2nd ed. — Berlin; Heidelberg: Springer Verlag, 2013. — xviii + 650 p. — ISBN 978-3-642-30957-1. — P. 86.

Источник

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

Re: Помогите найти Ближайшую прямую к точке

03.09.2009, 12:13

Заслуженный участник

11/05/08
32162

Точка лежит на прямой значи она делит

прямую на два луча

Да пусть себе делит. Жалко, что ли?…

gris

Re: Помогите найти Ближайшую прямую к точке

03.09.2009, 12:14

Заслуженный участник

13/08/08
14195

Надо повторить определения параллельных прямых, расстояния от точки до прямой, ближайшей прямой. Вопрос весьма не такой простой, как кажется. Надо доказать, что расстояние до второй прямой не может быть нулевым.

irok	Re: Помогите найти Ближайшую прямую к точке 03.09.2009, 12:17
03/09/09 10	Уважаемые господа математики дайте плиз ответ, а то у меня мозг взарвется от этой тупо-простой задачи

master

Re: Помогите найти Ближайшую прямую к точке

03.09.2009, 12:17

Заблокирован

12/08/09
∞
1284
Самодуровка

нет нежалко :lol:
но для самой этой точки есть луч с одной стороны и луч сдругой
а для любой другой точки не лежащей на прямой есть прямая

ewert

Re: Помогите найти Ближайшую прямую к точке

03.09.2009, 12:18

Заслуженный участник

11/05/08
32162

Вопрос весьма не такой простой, как кажется.

Не пудрите мозги человеку. Расстояние между двумя разными точками — по определению ненулевое.

irok	Re: Помогите найти Ближайшую прямую к точке 03.09.2009, 12:20
03/09/09 10	Тогда скиньте ссылку на аксиому, теорему что это доказывает

master

Re: Помогите найти Ближайшую прямую к точке

03.09.2009, 12:21

Заблокирован

12/08/09
∞
1284
Самодуровка

если точка касается прямой растояние между прямой иточкай равно 0

ewert

Re: Помогите найти Ближайшую прямую к точке

03.09.2009, 12:21

Заслуженный участник

11/05/08
32162

но для самой этой точки есть луч с одной стороны и луч сдругой

, а ещё для неё есть и она сама. “Палка, палка, огуречик — вот и вышел человечек…”

— Чт сен 03, 2009 13:22:36 —

если точка касается прямой

Точка не может касаться прямой. Точка вообще ничего не может “касаться”.

meduza

Re: Помогите найти Ближайшую прямую к точке

03.09.2009, 12:23

Заслуженный участник

03/06/09
1497

Напишите задачу дословно, если возможно. Много буков ниочем. Расстояние между точкой на прямой и самой этой прямой равно 0, но врядли кто мог придумать такую глупую задачу. Может вам нужно расстояние между прямыми найти?

irok	Re: Помогите найти Ближайшую прямую к точке 03.09.2009, 12:33
03/09/09 10	Дословная задача. Нарисуйте на клетчатой бумаге, где находятся точки, расстояние от которых до ближайшей горизонтальной линии сетки не больше, чем до ближайшей вертикальной. Я ее решила это форма песочных часов в клетке но не знаю основание писочных часов совпадает с горизонталами или они отступают о горизонталей в центр квадрата на расстояние в минус бесконечнрости? — Чт сен 03, 2009 13:36:09 — спасибо за ответ Может у кого есть другие варианты?

gris

Re: Помогите найти Ближайшую прямую к точке

03.09.2009, 12:37

Заслуженный участник

13/08/08
14195

Упс… Вот оно что. Ну если так, то совпадают. Даже в углах.

Мне, правда, больше нравится представление ответа в виде ромбиков. Поприкольнее как-то

ewert

Re: Помогите найти Ближайшую прямую к точке

03.09.2009, 12:38

Заслуженный участник

11/05/08
32162

или они отступают о горизонталей в центр квадрата на расстояние в минус бесконечнрости?

Неудачная шутка.

П.С. Учтите, что по условию задачи рисунок обязан периодически повторяться.

П.П.С. Выделение красным цветом запрещено правилами форума.

AKM

Re: Помогите найти Ближайшую прямую к точке

03.09.2009, 16:17

Заблокирован по собственному желанию

18/05/09
3612

!	irok, выделение красным цветом запрещено (зарезервировано для модераторских дел). Если Вы впервые на этом форуме, то просим обратить внимание на наши правила.

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

Данная статья рассказывает о теме «расстояния от точки до прямой», рассматриваются определения расстояния от точки к прямой с иллюстрированными примерами методом координат. Каждый блок теории в конце имеет показанные примеры решения подобных задач.

Расстояние от точки до прямой – определение

Расстояние от точки до прямой находится через определение расстояния от точки до точки. Рассмотрим подробней.

Пусть имеется прямая a и точка М1, не принадлежащая заданной прямой. Через нее проведем прямую b, расположенную перпендикулярно относительно прямой a. Точка пересечения прямых возьмем за Н1. Получим, что М1Н1 является перпендикуляром, который опустили из точки М1 к прямой a.

Определение 1

Расстоянием от точки М1 к прямой a называется расстояние между точками М1 и Н1.

Бывают записи определения с фигурированием длины перпендикуляра.

Определение 2

Расстоянием от точки до прямой называют длину перпендикуляра, проведенного из данной точки к данной прямой.

Определения эквивалентны. Рассмотрим рисунок, приведенный ниже.

Известно, что расстояние от точки до прямой является наименьшим из всех возможных. Рассмотрим это на примере.

Если взять точку Q, лежащую на прямой a, не совпадающую с точкой М1, тогда получим, что отрезок М1Q называется наклонной, опущенной из М1 к прямой a. Необходимо обозначить, что перпендикуляр из точки М1 является меньше, чем любая другая наклонная, проведенная из точки к прямой.

Чтобы доказать это, рассмотрим треугольник М1Q1Н1, где М1Q1 является гипотенузой. Известно, что ее длина всегда больше длины любого из катетов. Значим, имеем, что M1H1<M1Q. Рассмотрим рисунок, приведенный ниже.

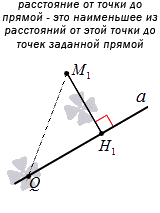
Расстояние от точки до прямой на плоскости – теория, примеры, решения

Исходные данные для нахождения от точки до прямой позволяют использовать несколько методов решения: через теорему Пифагора, определения синуса, косинуса, тангенса угла и другими. Большинство заданий такого типа решают в школе на уроках геометрии.

Когда при нахождении расстояния от точки до прямой можно ввести прямоугольную систему координат, то применяют метод координат. В данном пункте рассмотрим основных два метода нахождения искомого расстояния от заданной точки.

Первый способ подразумевает поиск расстояния как перпендикуляра, проведенного из М1 к прямой a. Во втором способе используется нормальное уравнение прямой а для нахождения искомого расстояния.

Если на плоскости имеется точка с координатами M1(x1, y1), расположенная в прямоугольной системе координат, прямая a, а необходимо найти расстояние M1H1, можно произвести вычисление двумя способами. Рассмотрим их.

Первый способ

Если имеются координаты точки H1, равные x2, y2, тогда расстояние от точки до прямой вычисляется по координатам из формулы M1H1=(x2-x1)2+(y2-y1)2.

Теперь перейдем к нахождению координат точки Н1.

Известно, что прямая линия в Оху соответствует уравнению прямой на плоскости. Возьмем способ задания прямой a через написание общего уравнения прямой или уравнения с угловым коэффициентом. Составляем уравнение прямой, которая проходит через точку М1 перпендикулярно заданной прямой a. Прямую обозначим буковой b. Н1 является точкой пересечения прямых a и b, значит для определения координат необходимо воспользоваться статьей, в которой идет речь о координатах точек пересечения двух прямых.

Видно, что алгоритм нахождения расстояния от заданной точки M1(x1, y1) до прямой a проводится согласно пунктам:

Определение 3

нахождение общего уравнения прямой a, имеющее вид A1x+B1y+C1=0 ,или уравнение с угловым коэффициентом, имеющее вид y=k1x+b1;
получение общего уравнения прямой b, имеющее вид A2x+B2y+C2=0 или уравнение с угловым коэффициентом y=k2x+b2, если прямая b пересекает точку М1 и является перпендикулярной к заданной прямой a;
определение координат x2, y2 точки Н1_,являющейся точкой пересечения a и b, для этого производится решение системы линейных уравнений A1x+B1y+C1=0A2x+B2y+C2=0 или y=k1x+b1y=k2x+b2;
вычисление искомого расстояния от точки до прямой, используя формулу M1H1=(x2-x1)2+(y2-y1)2.

Второй способ

Теорема способна помочь ответить на вопрос о нахождении расстояния от заданной точки до заданной прямой на плоскости.

Теорема

Прямоугольная система координат имеет Оху имеет точку M1(x1, y1), из которой проведена прямая а к плоскости, задаваемая нормальным уравнением плоскости, имеющее вид cos α·x+cos β·y-p=0, равно по модулю значению, получаемому в левой части нормального уравнения прямой, вычисляемому при x=x1, y=y1, значит, что M1H1=cos α·x1+cos β·y1-p.

Доказательство

Прямой а соответствует нормальное уравнение плоскости, имеющее вид cos α·x+cos β·y-p=0, тогда n→=(cos α, cos β) считается нормальным вектором прямой a при расстоянии от начала координат до прямой a с p единицами. Необходимо изобразить все данные на рисунке, добавить точку с координатами M1(x1, y1), где радиус-вектор точки М1 – OM1→=(x1, y1). Необходимо провести прямую от точки до прямой, которое обозначим M1H1. Необходимо показать проекции М2 и Н2 точек М1 и Н2 на прямую, проходящую через точку O с направляющим вектором вида n→=(cos α, cos β), а числовую проекцию вектора обозначим как OM1→=(x1, y1) к направлению n→=(cos α, cos β) как npn→OM1→.

Вариации зависят от расположения самой точки М1. Рассмотрим на рисунке, приведенном ниже.

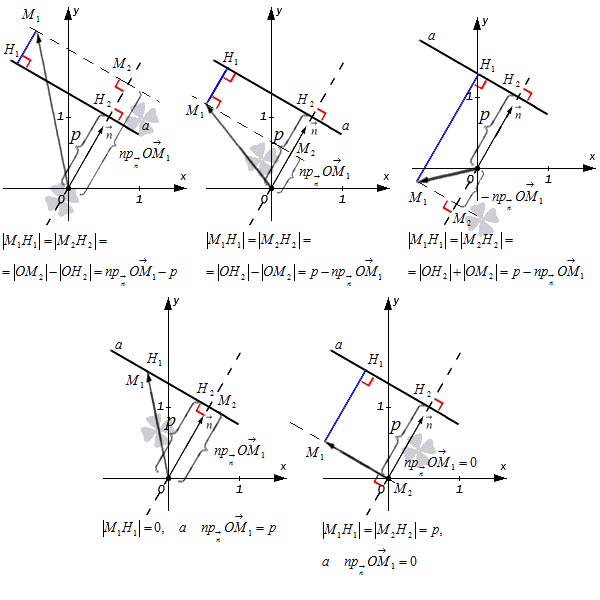
Результаты фиксируем при помощи формулы M1H1=npn→OM→1-p. После чего приводим равенство к такому виду M1H1=cos α·x1+cos β·y1-p для того, чтобы получить npn→OM→1=cos α·x1+cos β·y1.

Скалярное произведение векторов в результате дает преобразованную формулу вида n→, OM→1=n→·npn→OM1→=1·npn→OM1→=npn→OM1→, которая является произведением в координатной форме вида n→, OM1→=cos α·x1+cos β·y1. Значит, получаем, что npn→OM1→=cos α·x1+cos β·y1. Отсюда следует, что M1H1=npn→OM1→-p=cos α·x1+cos β·y1-p. Теорема доказана.

Получаем, что для нахождения расстояния от точки M1(x1, y1) к прямой a на плоскости необходимо выполнить несколько действий:

Определение 4

получение нормального уравнения прямой a cos α·x+cos β·y-p=0, при условии, что его нет в задании;
вычисление выраженияcos α·x1+cos β·y1-p, где полученное значение принимает M1H1.

Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости

Применим данные методы на решении задач с нахождением расстояния от точки до плоскости.

Пример 1

Найти расстояние от точки с координатами M1(-1, 2) к прямой 4x-3y+35=0.

Решение

Применим первый способ для решения.

Для этого необходимо найти общее уравнение прямой b, которая проходит через заданную точку M1(-1, 2), перпендикулярно прямой 4x-3y+35=0. Из условия видно, что прямая b является перпендикулярной прямой a, тогда ее направляющий вектор имеет координаты, равные(4, -3). Таким образом имеем возможность записать каноническое уравнение прямой b на плоскости, так как имеются координаты точки М1, принадлежит прямой b. Определим координаты направляющего вектора прямой b. Получим, что x-(-1)4=y-2-3⇔x+14=y-2-3. Полученное каноническое уравнение необходимо преобразовать к общему. Тогда получаем, что

x+14=y-2-3⇔-3·(x+1)=4·(y-2)⇔3x+4y-5=0

Произведем нахождение координат точек пересечения прямых, которое примем за обозначение Н1. Преобразования выглядят таким образом:

4x-3y+35=03x+4y-5=0⇔x=34y-3543x+4y-5=0⇔x=34y-3543·34y-354+4y-5=0⇔⇔x=34y-354y=5⇔x=34·5-354y=5⇔x=-5y=5

Из выше написанного имеем, что координаты точки Н1равны (-5;5).

Необходимо вычислить расстояние от точки М1 к прямой a. Имеем, что координаты точек M1(-1, 2) и H1(-5, 5), тогда подставляем в формулу для нахождения расстояния и получаем, что

M1H1=(-5-(-1)2+(5-2)2=25=5

Второй способ решения.

Для того, чтобы решить другим способом, необходимо получить нормальное уравнение прямой. Вычисляем значение нормирующего множителя и умножаем обе части уравнения 4x-3y+35=0. Отсюда получим, что нормирующий множитель равен -142+(-3)2=-15, а нормальное уравнение будет вида -15·4x-3y+35=-15·0⇔-45x+35y-7=0.

По алгоритму вычисления необходимо получить нормальное уравнение прямой и вычислить его со значениями x=-1, y=2. Тогда получаем, что

-45·-1+35·2-7=-5

Отсюда получаем, что расстояние от точки M1(-1, 2) к заданной прямой 4x-3y+35=0 имеет значение -5=5.

Ответ: 5.

Видно, что в данном методе важно использование нормального уравнения прямой, так как такой способ является наиболее коротким. Но первый метод удобен тем, что последователен и логичен, хотя имеет больше пунктов вычисления.

Пример 2

На плоскости имеется прямоугольная система координат Оху с точкой M1(8, 0) и прямой y=12x+1. Найти расстояние от заданной точки до прямой.

Решение

Решение первым способом подразумевает приведение заданного уравнения с угловым коэффициентом к уравнению общего вида. Для упрощения можно сделать иначе.

Если произведение угловых коэффициентов перпендикулярных прямых имеют значение -1, значит угловой коэффициент прямой перпендикулярной заданной y=12x+1 имеет значение 2. Теперь получим уравнение прямой, проходящее через точку с координатами M1(8, 0). Имеем, что y-0=-2·(x-8)⇔y=-2x+16.

Переходим к нахождению координат точки Н1, то есть точкам пересечения y=-2x+16 и y=12x+1. Составляем систему уравнений и получаем:

y=12x+1y=-2x+16⇔y=12x+112x+1=-2x+16⇔y=12x+1x=6⇔⇔y=12·6+1x=6=y=4x=6⇒H1(6, 4)

Отсюда следует, что расстояние от точки с координатами M1(8, 0) к прямой y=12x+1 равно расстоянию от точки начала и точки конца с координатами M1(8, 0) и H1(6, 4). Вычислим и получим, что M1H1=6-82+(4-0)220=25.

Решение вторым способом заключается в переходе от уравнения с коэффициентом к нормальному его виду. То есть получим y=12x+1⇔12x-y+1=0, тогда значение нормирующего множителя будет -1122+(-1)2=-25. Отсюда следует, что нормальное уравнение прямой принимает вид -25·12x-y+1=-25·0⇔-15x+25y-25=0. Произведем вычисление от точки M18, 0 к прямой вида -15x+25y-25=0. Получаем:

M1H1=-15·8+25·0-25=-105=25

Ответ: 25.

Пример 3

Необходимо вычислить расстояние от точки с координатами M1(-2, 4) к прямым 2x-3=0 и y+1=0.

Решение

Получаем уравнение нормального вида прямой 2x-3=0:

2x-3=0⇔12·2x-3=12·0⇔x-32=0

После чего переходим к вычислению расстояния от точки M1-2, 4 к прямой x-32=0. Получаем:

M1H1=-2-32=312

Уравнение прямой y+1=0 имеет нормирующий множитель со значением равным -1. Это означает, что уравнение примет вид -y-1=0. Переходим к вычислению расстояния от точки M1(-2, 4) к прямой -y-1=0. Получим, что оно равняется -4-1=5.

Ответ: 312 и 5.

Подробно рассмотрим нахождение расстояния от заданной точки плоскости к координатным осям Ох и Оу.

В прямоугольной системе координат у оси Оу имеется уравнение прямой, которое является неполным имеет вида х=0, а Ох – y=0. Уравнения являются нормальными для осей координат, тогда необходимо найти расстояние от точки с координатами M1x1, y1 до прямых. Это производится, исходя из формул M1H1=x1 и M1H1=y1. Рассмотрим на рисунке, приведенном ниже.

Пример 4

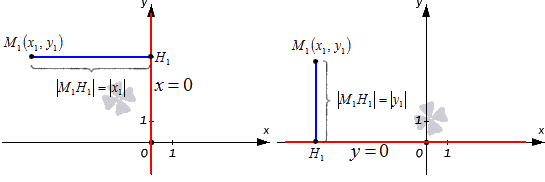
Найти расстояние от точки M1(6, -7) до координатных прямых, расположенных в плоскости Оху.

Решение

Так как уравнение у=0 относится к прямой Ох, можно найти расстояние от M1 с заданными координатами, до этой прямой, используя формулу. Получаем, что 6=6.

Так как уравнение х=0 относится к прямой Оу, то можно найти расстояние от М1 к этой прямой по формуле. Тогда получим, что -7=7.

Ответ: расстояние от М1к Ох имеет значение 6, а от М1к Оу имеет значение 7.

Расстояние от точки до прямой в пространстве – теория, примеры, решения

Когда в трехмерном пространстве имеем точку с координатами M1(x1, y1, z1), необходимо найти расстояние от точки A до прямой a.

Рассмотрим два способа, которые позволяют производить вычисление расстояние от точки до прямой a, расположенной в пространстве. Первый случай рассматривает расстояние от точки М1 к прямой, где точка на прямой называется Н1 и является основанием перпендикуляра, проведенного из точки М1 на прямую a. Второй случай говорит о том, что точки этой плоскости необходимо искать в качестве высоты параллелограмма.

Первый способ

Из определения имеем, что расстояние от точки М1_,расположенной на прямой а, является длиной перпендикуляра М1Н1_,тогда получим, что при найденных координатах точки Н1 , тогда найдем расстояние между M1(x1, y1, z1) и H1(x1, y1, z1), исходя из формулы M1H1=x2-x12+y2-y12+z2-z12.

Получаем, что все решение идет к тому, чтобы найти координаты основания перпендикуляра, проведенного из М1 на прямую a. Это производится следующим образом: Н1 является точкой, где пересекаются прямая a с плоскостью, которая проходит через заданную точку.

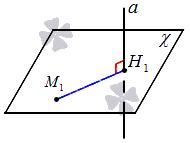
Значит, алгоритм определения расстояния от точки M1(x1, y1, z1) к прямой a пространства подразумевает несколько пунктов:

Определение 5

составление уравнение плоскости χ в качестве уравнения плоскости, проходящего через заданную точку, находящуюся перпендикулярно прямой;
определение координат (x2, y2, z2), принадлежавших точке Н1, которая является точкой пересечения прямой a и плоскости χ;
вычисление расстояния от точки до прямой при помощи формулы M1H1=x2-x12+y2-y12+z2-z12.

Второй способ

Из условия имеем прямую a, тогда можем определить направляющий вектор a→=ax, ay, az с координатами x3, y3, z3 и определенной точки М3_,принадлежащей прямой a. При наличии координат точек M1(x1, y1) и M3x3, y3, z3 можно произвести вычисление M3M1→:

M3M1→=(x1-x3, y1-y3, z1-z3)

Следует отложить векторы a→=ax, ay, az и M3M1→=x1-x3, y1-y3, z1-z3 из точки М3, соединим и получим фигуру параллелограмма. М1Н1 является высотой параллелограмма.

Рассмотрим на рисунке, приведенном ниже.

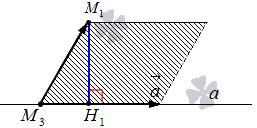
Имеем, что высота М1Н1 является искомым расстоянием, тогда необходимо найти его по формуле. То есть ищем M1H1.

Обозначим площадь параллелограмма за букву S, находится по формуле, используя вектор a→=(ax, ay, az) и M3M1→=x1-x3. y1-y3, z1-z3. Формула площади имеет вид S=a→×M3M1→. Также площадь фигуры равняется произведению длин его сторон на высоту, получим, что S=a→·M1H1 с a→=ax2+ay2+az2, являющимся длиной вектора a→=(ax, ay, az), являющейся равной стороне параллелограмма. Значит, M1H1 является расстоянием от точки до прямой. Ее нахождение производится по формуле M1H1=a→×M3M1→a→.

Для нахождения расстояния от точки с координатами M1(x1, y1, z1) до прямой a в пространстве, необходимо выполнить несколько пунктов алгоритма:

Определение 6

определение направляющего вектора прямой a – a→=(ax, ay, az);
вычисление длины направляющего вектора a→=ax2+ay2+az2;
получение координат x3, y3, z3, принадлежавших точке М₃, находящейся на прямой а;
вычисление координат вектора M3M1→;
нахождение векторного произведения векторов a→(ax, ay, az) и M3M1→=x1-x3, y1-y3, z1-z3 в качестве a→×M3M1→=i→j→k→axayazx1-x3y1-y3z1-z3 для получения длины по формуле a→×M3M1→;
вычисление расстояния от точки до прямой M1H1=a→×M3M1→a→.

Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве

Пример 5

Найти расстояние от точки с координатами M12, -4, -1 к прямой x+12=y-1=z+55.

Решение

Первый способ начинается с записи уравнения плоскости χ, проходящей через М1и перпендикулярно заданной точке. Получаем выражение вида:

2·(x-2)-1·(y-(-4))+5·(z-(-1))=0⇔2x-y+5z-3=0

Нужно найти координаты точки H1, являющейся точкой пересечения с плоскостью χ к заданной по условию прямой. Следует переходить от канонического вида к пересекающемуся. Тогда получаем систему уравнений вида:

x+12=y-1=z+55⇔-1·(x+1)=2·y5·(x+1)=2·(z+5)5·y=-1·(z+5)⇔x+2y+1=05x-2z-5=05y+z+5=0⇔x+2y+1=05x-2z-5=0

Необходимо вычислить систему x+2y+1=05x-2z-5=02x-y+5z-3=0⇔x+2y=-15x-2z=52x-y+5z=3 по методу Крамера, тогда получаем, что:

∆=12050-22-15=-60∆x=-12050-23-15=-60⇔x=∆x∆=-60-60=1∆y=1-10552235=60⇒y=∆y∆=60-60=-1∆z=12-15052-13=0⇒z=∆z∆=0-60=0

Отсюда имеем, что H1(1, -1, 0).

Необходимо рассчитать расстояние между точками с координатами M1(2, -4, -1) и H1(1, -1, 0) по формуле:

M1H1=1-22+-1–42+0–12=11

Второй способ необходимо начать с поиска координат в каноническом уравнении. Для этого необходимо обратит внимание на знаменатели дроби. Тогда a→=2, -1, 5 является направляющим вектором прямой x+12=y-1=z+55. Необходимо вычислить длину по формуле a→=22+(-1)2+52=30.

Понятно, что прямая x+12=y-1=z+55 пересекает точку M3(-1, 0, -5), отсюда имеем, что вектор с началом координат M3(-1, 0, -5) и его концом в точке M12, -4, -1 является M3M1→=3, -4, 4. Находим векторное произведение a→=(2, -1, 5) и M3M1→=(3, -4, 4).

Мы получаем выражение вида a→×M3M1→=i→j→k→2-153-44=-4·i→+15·j→-8·k→+20·i→-8·j→=16·i→+7·j→-5·k→

получаем, что длина векторного произведения равняется a→×M3M1→=162+72+-52=330.

Имеются все данные для использования формулы вычисления расстояния от точки для прямлой, поэтому применим ее и получим:

M1H1=a→×M3M1→a→=33030=11

Ответ: 11.

Источник

9 / 9 / 6

Регистрация: 16.10.2011

Сообщений: 423

На прямой найти точку ближайшую к точке

22.01.2015, 19:36. Показов 22270. Ответов 11

Дана прямая $https://www.cyberforum.ru/cgi-bin/latex.cgi?l:frac{x}{1}=frac{y+7}{2}=frac{z-3}{-1}$ . Необходимо найти на ней точку ближайшую к точке А(3,2,6). Составил парам. ур-ие этой прямой $https://www.cyberforum.ru/cgi-bin/latex.cgi?begin{cases} & x=t \ & y=2t-7 \ & z=-t+3 end{cases}$ , а вот что делать дальше не знаю. Была идея написать ур-ие перпендикуляра и найти точку пересечения плоскостей, но реализовать не получилось.

1765 / 969 / 180

Регистрация: 24.02.2013

Сообщений: 2,783

Записей в блоге: 12

22.01.2015, 20:07

Сообщение было отмечено serega006 как решение

Решение

Через точку А проведите плоскость перпендикулярную заданной прямой.Найдите точку пересечения прямой и плоскости, получите искомую точку.

9 / 9 / 6

Регистрация: 16.10.2011

Сообщений: 423

22.01.2015, 21:12

[ТС]

Перевел прямую в общий вид 2x-y+2z-13=0, снял вектор нормали n(2;-1;2), составил уравнение прямой перпендикулярной данной. $https://www.cyberforum.ru/cgi-bin/latex.cgi?frac{x-3}{2}=frac{y-2}{-1}=frac{z-6}{2}$ . Составил систему $https://www.cyberforum.ru/cgi-bin/latex.cgi?begin{cases} & 2x-y+2z-13=0 \ & frac{x-3}{2}=frac{y-2}{-1} \ & frac{y-2}{-1}=frac{z-6}{2} end{cases}$ => $https://www.cyberforum.ru/cgi-bin/latex.cgi?begin{cases} & 2x-y+2z-13=0 \ & x+2y-7=0\ & -2y-z+10=0end{cases}$ . Решив эту систему получил x=7/3 y=7/3 z=16/3. Спасибо.

1765 / 969 / 180

Регистрация: 24.02.2013

Сообщений: 2,783

Записей в блоге: 12

22.01.2015, 22:00

Вы неверно записали уравнение плоскости, проходящей через точку А, перпендикулярно заданной прямой.
Правильно будет x+2y-z-1=0

9 / 9 / 6

Регистрация: 16.10.2011

Сообщений: 423

22.01.2015, 22:07

[ТС]

Сообщение от Nacuott

x+2y-z-1=0

я составил не плоскость, а прямую перпендикулярную моей прямой. А потом представил ее как пересечение двух плоскостей и имея три уравнения плоскости составил систему и нашел точку.

1765 / 969 / 180

Регистрация: 24.02.2013

Сообщений: 2,783

Записей в блоге: 12

22.01.2015, 22:34

Вот верное решение

Миниатюры

9 / 9 / 6

Регистрация: 16.10.2011

Сообщений: 423

22.01.2015, 23:16

[ТС]

Не могу понять откуда у вас взялось 3 ур-ие $https://www.cyberforum.ru/cgi-bin/latex.cgi?frac{y+z}{2}=frac{z-3}{-1}$ ? разве не $https://www.cyberforum.ru/cgi-bin/latex.cgi?frac{y+7}{2}=frac{z-3}{-1}$ должно быть?

6353 / 4062 / 1509

Регистрация: 09.10.2009

Сообщений: 7,550

Записей в блоге: 4

22.01.2015, 23:33

Сообщение было отмечено serega006 как решение

Решение

Nacuott, если решать по-олдскульному, то у меня вышла точка
Проверка:
1) Точка лежит на данной прямой, ибо $https://www.cyberforum.ru/cgi-bin/latex.cgi?frac{3}{1}=frac{-1+7}{2}=frac{0-3}{-1}=3$
2) Вектор из этой проекции в данную точку А(3;2;6) равен и он перпендикулярен направляющему вектору данной прямой – , значит, найденная точка лежит на перпендикуляре от А к данной прямой.

1765 / 969 / 180

Регистрация: 24.02.2013

Сообщений: 2,783

Записей в блоге: 12

22.01.2015, 23:35

Сообщение было отмечено serega006 как решение

Решение

Ясно-описка.Должно быть так.

Миниатюры

9 / 9 / 6

Регистрация: 16.10.2011

Сообщений: 423

22.01.2015, 23:45

[ТС]

Я уж испугался что ответов не сколько Спасибо огромное

8717 / 6316 / 3394

Регистрация: 14.01.2014

Сообщений: 14,496

23.01.2015, 09:01

Задачу можно было решить чисто алгебраически через минимум расстояния от заданной точки до точки на прямой: , который достигается в точке $https://www.cyberforum.ru/cgi-bin/latex.cgi?t_0=frac{36}{2cdot 6}=3$ отсюда искомая точка

1765 / 969 / 180

Регистрация: 24.02.2013

Сообщений: 2,783

Записей в блоге: 12

23.01.2015, 22:06

Ну, давайте запустим снаряд по-мощнее – метод Лагранжа с условным экстремумом (не надо переходить к параметрическому уравнению прямой

Миниатюры

IT_Exp

Эксперт

87844 / 49110 / 22898

Регистрация: 17.06.2006

Сообщений: 92,604

23.01.2015, 22:06

Помогаю со студенческими работами здесь

Найти точку Q, симметричную точке Р относительно прямой
Помогите с задачкой

Найти точку Q, симметричную точке Р относительно прямой

Найти точку А1, симметричную точке А (8,1,4)относительно прямой
Найти точку А1, симметричную точке А (8,1,4) относительно прямой g:x+7/1=y+5/4=z/1

Найти точку, симметричную заданной точке относительно прямой
найти точку Р, симметричную точке М(8,-9)относительно прямой ,проходящей через точки А(3,-4), и…

Найти точку N, симметричную точке M относительно данной прямой
Задача 3. Найти точку N, симметричную точке M(0;-3;-2) относительно данной прямой….

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

Источник

Пересечение окружности и прямой

Дана окружность (координатами своего центра и радиусом) и прямая (своим уравнением). Требуется найти точки их пересечения (одна, две, либо ни одной).

Решение

Вместо формального решения системы двух уравнений подойдём к задаче с геометрической стороны (причём, за счёт этого мы получим более точное решение с точки зрения численной устойчивости).

Предположим, не теряя общности, что центр окружности находится в начале координат (если это не так, то перенесём его туда, исправив соответствующе константу C в уравнении прямой). Т.е. имеем окружность с центром в (0,0) радиуса r и прямую с уравнением Ax + By + C = 0.

Сначала найдём ближайшую к центру точку прямой – точку с некоторыми координатами (x₀,y₀). Во-первых, эта точка должна находиться на таком расстоянии от начала координат:

Во-вторых, поскольку вектор (A,B) перпендикулярен прямой, то координаты этой точки должны быть пропорциональны координатам этого вектора. Учитывая, что расстояние от начала координат до искомой точки нам известно, нам нужно просто нормировать вектор (A,B) к этой длине, и мы получаем:

(здесь неочевидны только знаки ‘минус’, но эти формулы легко проверить подстановкой в уравнение прямой – должен получиться ноль)

Зная ближайшую к центру окружности точку, мы уже можем определить, сколько точек будет содержать ответ, и даже дать ответ, если этих точек 0 или 1.

Действительно, если расстояние от (x₀, y₀) до начала координат (а его мы уже выразили формулой – см. выше) больше радиуса, то ответ – ноль точек. Если это расстояние равно радиусу, то ответом будет одна точка – (x₀,y₀). А вот в оставшемся случае точек будет две, и их координаты нам предстоит найти.

Итак, мы знаем, что точка (x₀, y₀) лежит внутри круга. Искомые точки (ax,ay) и (bx,by), помимо того что должны принадлежать прямой, должны лежать на одном и том же расстоянии d от точки (x₀, y₀), причём это расстояние легко найти:

Заметим, что вектор (-B,A) коллинеарен прямой, а потому искомые точки (ax,ay) и (bx,by) можно получить, прибавив к точке (x₀,y₀) вектор (-B,A), нормированный к длине d (мы получим одну искомую точку), и вычтя этот же вектор (получим вторую искомую точку).

Окончательное решение такое:

Если бы мы решали эту задачу чисто алгебраически, то скорее всего получили бы решение в другом виде, которое даёт бОльшую погрешность. Поэтому “геометрический” метод, описанный здесь, помимо наглядности, ещё и более точен.

Реализация

Как и было указано в начале описания, предполагается, что окружность расположена в начале координат.

Поэтому входные параметры – это радиус окружности и коэффициенты A,B,C уравнения прямой.

Планиметрия (прямая и окружность)

Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).

Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.

1.1 Построить угол 60° с заданой стороной

1.2 Построить серединный перпендикуляр к отрезку

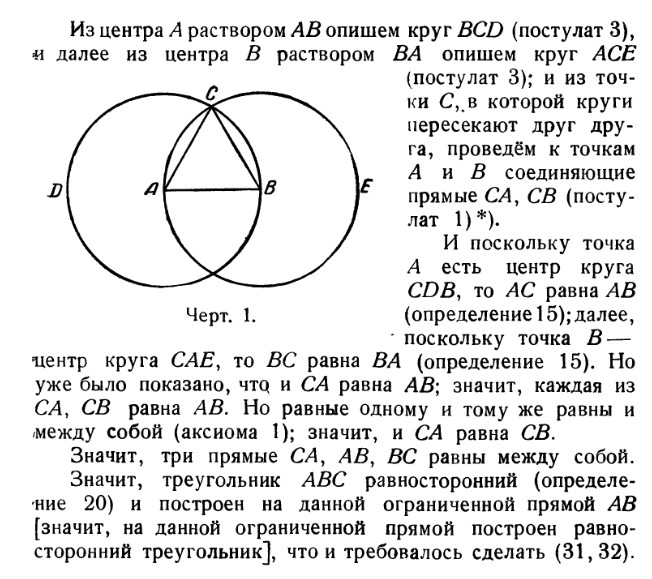
На данной ограниченной прямой построить равносторонний треугольник

1.3 Середина отрезка

всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.

Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.

любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.

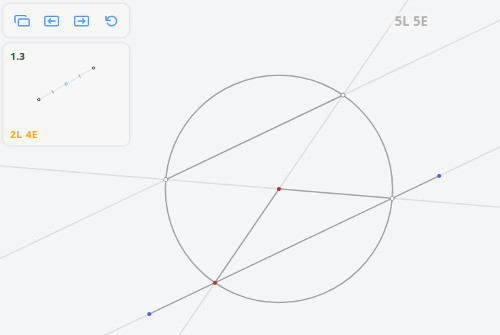
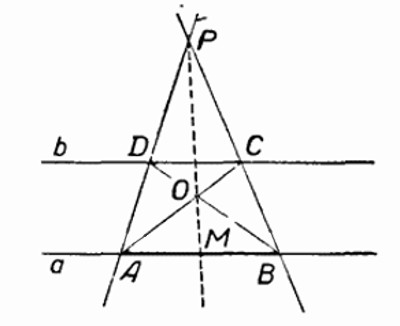
Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.

Решением задачи 1.3 по методу Штейнера-Понеселе будет:

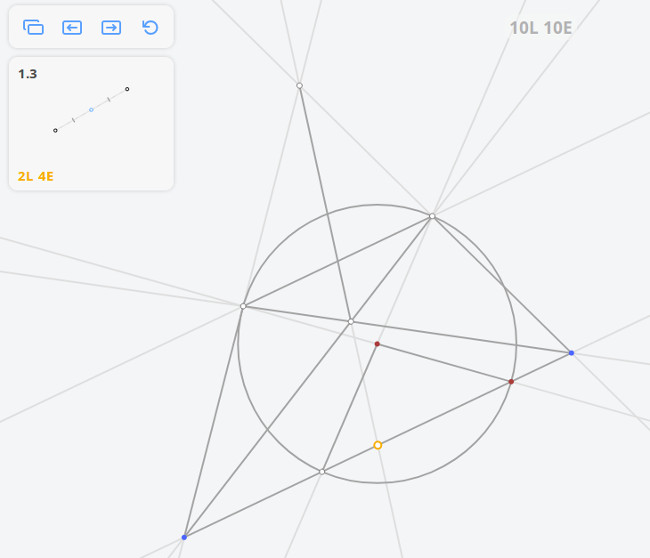
1.4 Окружность, вписанная в квадрат

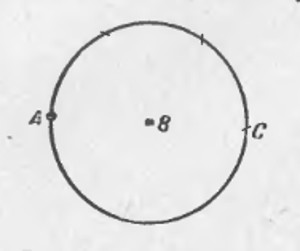
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.

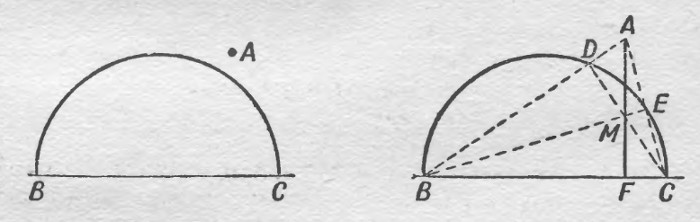
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.

И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой

1.6 Найти центр окружности

Плоский угол, опирающийся на диаметр окружности, — прямой.

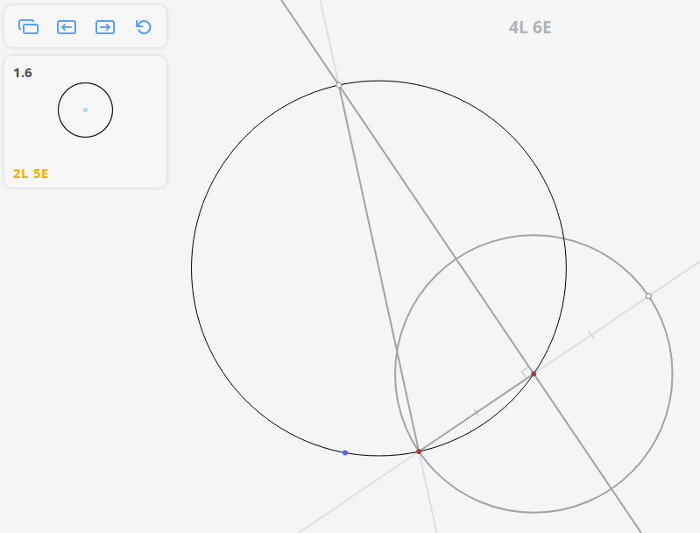
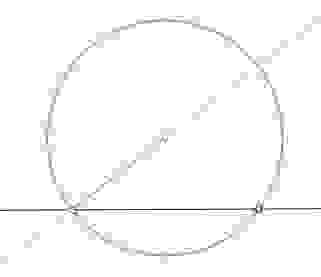
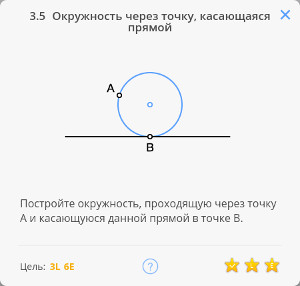
Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса

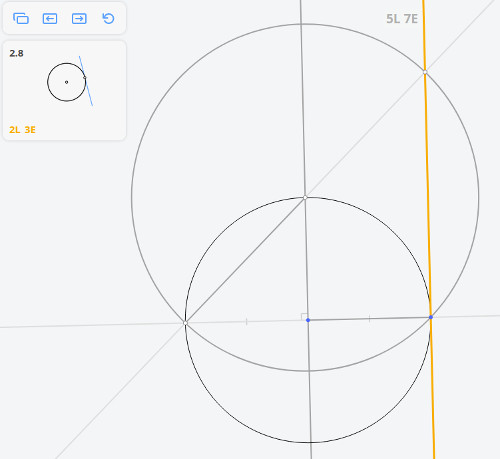
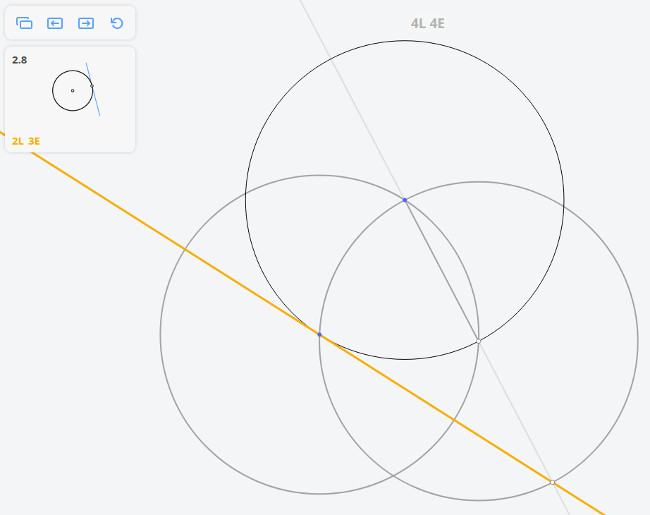
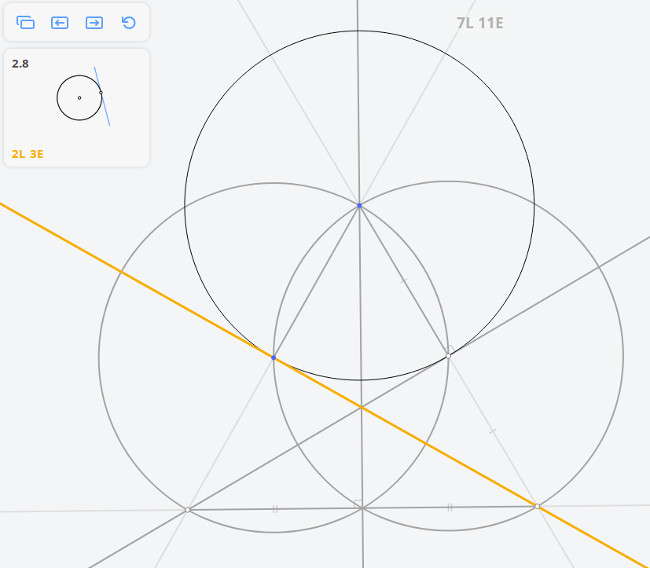
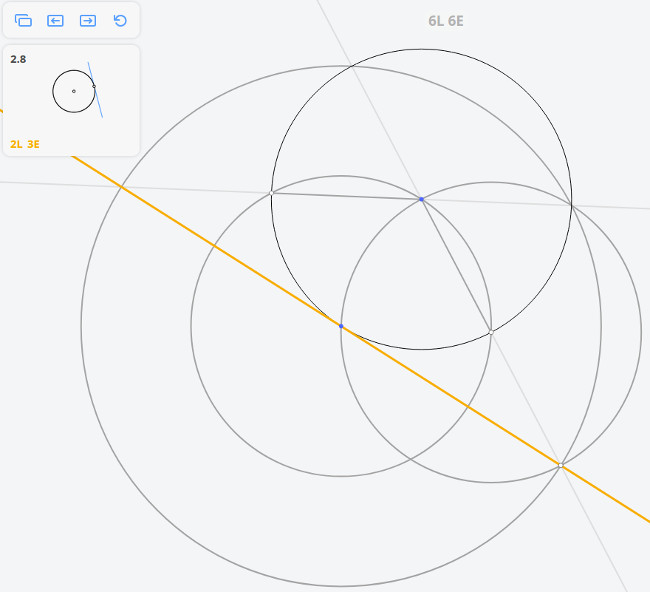
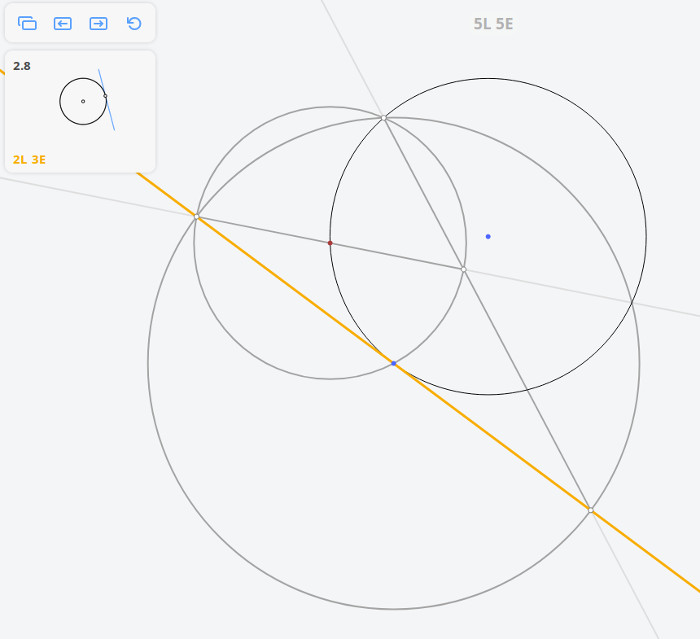
Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.

Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка

1.7 Квадрат, вписанный в окружность

Задача Наполеона

Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом

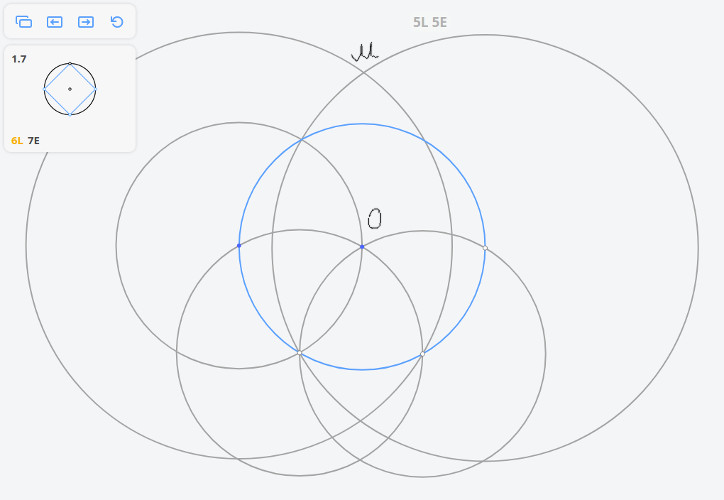
В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом

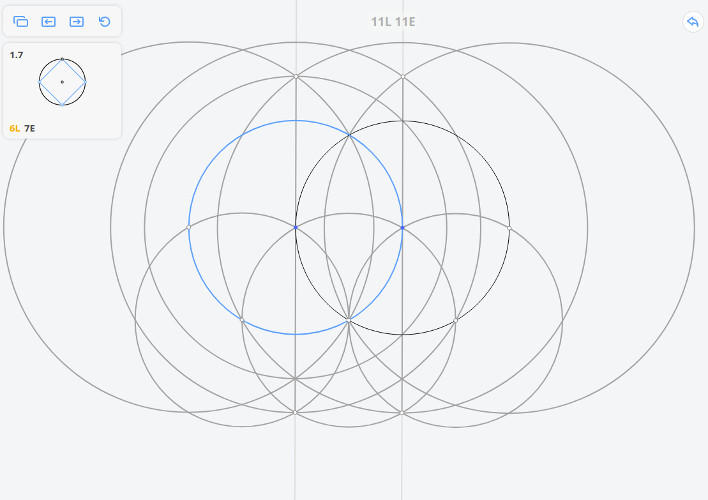
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО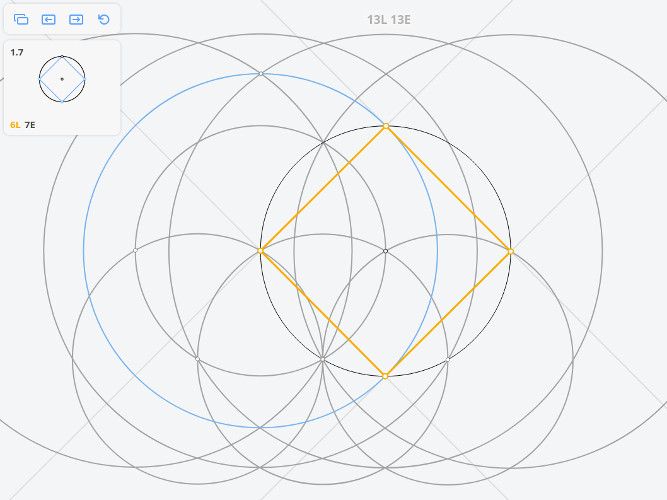

Пересечение окружности и прямой.Координаты.

Элементы окружности или координаты

x^2+y^2+ x+ y+ =0

Элементы прямой линии

Уравнение окружности

Уравнение прямой к угловым коэффициентом

Координаты пересечения окружности и прямой

Рассмотрим более подробно задачу пересечения окружности и прямой. В принципе само решение есть уже в общем виде Пересечение прямой и кривой второго порядка, но мы рассмотрим и выведем формулы точек пересечения этих двух геометрических объектов.

Уравнение прямой, как мы знаем из материала Расчет параметров прямой линии по заданным параметрам могут быть заданы в нескольких видах:

– с угловым коэффициентом

– в нормальном виде

Что бы решить нашу первоначальную задачу, использовать будем уравнение прямой с угловым коэффициентом которое имеет вид

Уравнение окружности тоже может быть выражена в различных видах

Например в общем виде оно имеет вид

Подставим в уравнение окружности, уравнение прямой

Мы получили стандартное квадратное уравнение, решив котрое мы получим два значения, которые и будут являтся абсциссами точек пересечения прямой и окружности.

Подставим эти координаты в уравнение прямой, мы получим две ординаты точек пересечения.

Таким образом решение найдено.

Для упрощения, для сверки результатов – калькулятор помогает Вам рассчитать эти точки. Интересная особенность состоит в том, что прямая может быть задана в любом виде, хоть виде двух точек.

А уравнение окружности может быть не только введено с помощью коэффицентов, но и в виде пары трех координат через которые, эта окружность будет проходить.

[spoiler title=”источники:”]

http://habr.com/ru/post/478410/

http://abakbot.ru/online-16/230-peresechenie-okruzhnosti-i-pryamoj

[/spoiler]

Источник

Декартова система координат[править | править код]

Прямая задана уравнением[править | править код]

Прямая задана двумя точками[править | править код]

Доказательства[править | править код]

Алгебраическое доказательство[править | править код]

Геометрическое доказательство[править | править код]

Доказательство с помощью проекции вектора[править | править код]

Другие формулы[править | править код]

Формулировка с помощью векторов[править | править код]

Другая формулировка с помощью векторов[править | править код]

Обобщения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Дополнительная литература[править | править код]

Правила форума

Кто сейчас на конференции

Расстояние от точки до прямой – определение

Расстояние от точки до прямой на плоскости – теория, примеры, решения

Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости

Расстояние от точки до прямой в пространстве – теория, примеры, решения

Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве

На прямой найти точку ближайшую к точке

Решение

Решение

Решение

Пересечение окружности и прямой

Решение

Реализация

Планиметрия (прямая и окружность)

1.1 Построить угол 60° с заданой стороной

1.2 Построить серединный перпендикуляр к отрезку

1.3 Середина отрезка

1.4 Окружность, вписанная в квадрат

1.6 Найти центр окружности

1.7 Квадрат, вписанный в окружность

Задача Наполеона

Пересечение окружности и прямой.Координаты.

Вам также может понравиться

Как найти залипшую клавишу на ноутбуке

Как составить облако мыслей

Как найти искаженный лес в аду

Добавить комментарий Отменить ответ