Пирамида – это объемная многогранная геометрическая фигура, состоящая из основания и треугольных
граней, собирающихся в одной точке. У нее есть: вершина, ребра (боковые и основные), боковые грани,
основание, высота и апофема – прямая, соединяющая вершину с границей вписанной в основание
окружности. Правильная пирамида –та, у которой все боковые ребра равны и находятся под одним углом к
основанию, а вершина проецируется на центр окружности, описанной вокруг основания. Тетраэдр –
частный случай правильной пирамиды, в которой боковые ребра равны основным и между собой.
Боковые ребра правильной пирамиды – выходящие из ее вершины, общие для боковых граней стороны. Длина
бокового ребра обозначается латинской буквой «b». Это одно из базовых значений, через которое можно
найти остальные элементы пирамиды. Во многих математических задачах требуется вычислить его или
подставить в формулы.
- Боковое ребро правильной треугольной пирамиды через высоту
и ребро основания - Боковое ребро правильной треугольной пирамиды через высоту
и радиус описанной окружности вокруг правильной треугольной пирамиды - Ребро основания правильной треугольной пирамиды через обьём
и высоту
Ребро основания правильной треугольной пирамиды через объём и высоту
Та часть пространства, которую занимает правильная треугольная пирамида называется ее объемом.
Является физической величиной. Его можно найти через, например, через высоту и сторону основания.
Если нам известен объем и высота правильной треугольной пирамиды, то не составит особого труда найти
ребро основания. Для этого используется формула:
a = √((V * 4 * √3) / H)
где V — объём, H — высота.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретную задачу. Необходимо найти ребро основания, зная что
высота H равна 56 см, a объем 268 см³, подставив все в формулу получим следующий результат: a = √((V * 4 * √3) / H) = √((268 * 4 * √3) / 56) = 5,76 см. Боковое
ребро (b) = 5,76 см.
Боковое ребро правильной треугольной пирамиды через высоту и ребро основания
Боковое ребро правильной пирамиды можно найти по теореме Пифагора, поскольку высота, опущенная в
основание пирамиды, опускается в центр вписанной и описанной окружности для данного многоугольника.
Таким образом формула для нахождения бокового ребра правильной треугольной пирамиды через высоту и
ребро основания будет следующей:
b = √(H² + (a / 2 sin (60º)²))
где H — высота, a — ребро основания.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретные данные. Пусть высота H равна 44 мм, a ребро основания
a равно 63 мм, подставив все в формулу получим следующий результат: b = √(H² + (a / 2 sin (60º)²)) = √(44² + (63 / 2 sin (60º)²)) = 57,09 мм.
Боковое ребро (b) = 57.08765 мм.
Боковое ребро правильной треугольной пирамиды через высоту и радиус описанной окружности вокруг
правильной треугольной пирамиды
Если пирамида вписана в окружность, то ее называют описанной вокруг пирамиды. Около пирамиды можно
описать сферу тогда и только тогда, когда около основания пирамиды можно описать
окружность. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее
основания, является центром описанной около основания окружности. Если нам известна высота и радиус
этой описанной окружности, то мы сможем найти боковое ребро. Формула подходит только для правильной
треугольной пирамиды:
b = √(H² + R²)
где H — высота правильной треугольной пирамиды, R — радиус описанной вокруг
окружности.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретные данные. Пусть высота H равна 73 мм, a радиус описанной
вокруг окружности 114 мм, подставив все в формулу получим следующий результат: b = √(H² + R²) = √(73² + 114²) = 135 мм. Боковое
ребро (b) = 135 мм.
Почти все формулы пирамиды основываются на теореме Пифагора. Таким образом, можно вывести боковое
ребро правильной треугольной пирамиды через высоту и радиус описанной окружности, опираясь на
прямоугольный треугольник, гипотенуза которого является искомой величиной. По одному из основных
свойств правильной пирамиды, ее высота соединяет вершину с центрами окружностей, вписанных и
описанных вокруг пирамиды. Так внутри формируются 2 треугольника с углом 90°. Один состоит из
высоты, бокового ребра и соединяет их с радиусом описанной окружности, другой составляет высота и
апофема, соединённые с радиусом вписанной окружности.
Правильная пирамида – это геометрическое тело, образованное правильным многоугольником, лежащим в основании и боковыми ребрами, подымающимися в одну вершину из всех углов основания. Такая пирамида является типовой, поскольку обладает множеством свойств за счет своего основания. Помимо того, что все боковые грани представляют собой конгруэнтные треугольники, а все боковые ребра равны (также как и ребра в основании между собой), высота правильной пирамиды опускается ровно в центр вписанной и описанной окружностей для заданного многоугольника. Поэтому в такой пирамиде возникает сразу два прямоугольных треугольника во внутреннем пространстве, один из них соединяет высоту с апофемой радиусом вписанной окружности, а второй соединяет высоту с боковым ребром радиусом описанной окружности.
Таким образом, для того, чтобы найти боковое ребро пирамиды, необходимо знать лишь сторону основания, общее количество сторон этого же многоугольника и высоту. По теореме Пифагора, боковое ребро является гипотенузой и, следовательно, находится сложением:

Подставив в формулу значение радиуса описанной окружности для правильного многоугольника, получаем окончательный ее вид:

Задания
Версия для печати и копирования в MS Word
Тип 2 № 76763 
i
В правильной четырехугольной пирамиде высота равна 4, объем равен 280. Найдите боковое ребро этой пирамиды.
Решение.
Это задание ещё не решено, приводим решение прототипа.
В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
Объем пирамиды с площадью основания S и высотой h равен откуда площадь основания
Сторона основания тогда
а диагональ
Боковое ребро найдем по теореме Пифагора:
Ответ: 13.
Аналоги к заданию № 27178: 76715 76717 76719 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Прототип задания
·
Видеокурс
Пирамида и ее боковые ребра. Формулы. Боковое ребро пирамиды Хеопса

Одной из геометрических фигур, свойства которых изучают в школах в курсе стереометрии, является пирамида. Рассмотрим, что собой представляет эта фигура, а также подробно охарактеризуем важный линейный параметр – боковое ребро пирамиды.
Пирамида как фигура геометрии
Прежде чем рассматривать понятие о боковом ребре пирамиды, следует дать определение этой пространственной фигуры. Если говорить коротко, то пирамида представляет собой поверхность, ограниченную одним n-угольником и n треугольниками. Рисунок ниже показывает один из возможных вариантов этой фигуры.
С геометрической точки зрения получить пирамиду можно таким способом: взять n-угольник и соединить все его углы с некоторой точкой в пространстве, которая не должна лежать в плоскости n-угольника.
Заметим, что, независимо от количества сторон n в исходном многоугольнике, всегда при соединении его углов с единственной точкой получаются треугольники. Их совокупность образует боковую поверхность пирамиды, а исходный многоугольник является ее основанием. Точка, в которой соединяются все треугольники, получила название вершины пирамиды.
Элементы пирамиды
Каждая пирамида образована тремя главными элементами:
- гранями;
- ребрами;
- вершинами.
Граней или сторон у фигуры всегда n + 1. Это легко видеть на приведенном в предыдущем пункте рисунке. Шестиугольное основание является одной гранью. Оставшиеся 6 сторон представляют собой треугольники, опирающиеся на стороны основания и пересекающиеся в вершине пирамиды.
Ребра представляют собой совокупность точек пересечения соседних граней. Фигура имеет два типа этих элементов:
- ребра основания;
- боковые ребра пирамиды.
Их количества, независимо от числа сторон n основания, всегда равны друг другу, то есть фигура имеет 2 × n ребер. Если с ребрами основания все понятно (они являются сторонами n-угольника), то для боковых ребер следует уточнить, что они представляют собой отрезки, соединяющие углы основания с высотой рассматриваемой фигуры.
Наконец, третьим типом элементов пирамиды будут вершины. У фигуры имеется n + 1 вершина. Однако n из них образованы основанием и двумя боковыми гранями. Лишь одна единственная вершина не связана с основанием. Она играет важную роль при изучении количественных характеристик пирамиды, например, ее высоты или апофемы.
Правильные пирамиды
Пирамиды могут быть наклонными и прямыми, правильными и неправильными, выпуклыми и вогнутыми. Все названные типы фигур отличаются друг от друга многоугольным основанием и особенностями поведения высоты.
Предположим, что имеется пирамида, у которой высота (опущенный из вершины к основанию перпендикуляр) падает на многоугольник точно в его геометрическом центре. В этом случая фигура называется прямой. Если же многоугольник является равносторонним, то помимо прямой, пирамида также будет правильной. Напомним, что центр геометрический плоской фигуры аналогичен центру масс в физике. Для квадрата он совпадает с точкой пересечения диагоналей, а для треугольника – с точкой, где медианы пересекаются.
Пирамиды правильные удобно изучать ввиду их симметрии. Так, боковые ребра правильной пирамиды и ее боковые грани равны друг другу. Частным случаем является ситуация, когда боковые грани будут образованы равносторонними треугольниками.
Далее рассмотрим, какими формулами следует пользоваться, чтобы определить размеры боковых ребер пирамид — правильной четырехугольной и треугольной.
Треугольная пирамида
Существуют четыре линейных параметра, которые описывают размеры правильной пирамиды. К ним относятся сторона основания a, боковое ребро b, высота h и апофема hb. Ниже приведем формулы, которые позволяют рассчитать длину бокового ребра для треугольной пирамиды правильной. Основание этой фигуры представляет треугольник с равными сторонами, что позволяет записать следующие равенства:
Обе формулы являются следствием теоремы Пифагора для треугольников, в которых боковое ребро b является гипотенузой.
Четырехугольная пирамида
Эта фигура, пожалуй, является самой известной среди остальных пирамид благодаря величественным древним египетским сооружениям. Боковое ребро пирамиды четырехугольной правильной можно определить по таким формулам:
Как и в предыдущем случае, эти выражения являются следствием свойства катетов и гипотенузы прямоугольного треугольника.
Отметим, что формула расчета бокового ребра правильной пирамиды четырехугольной через ее апофему и сторону основания аналогична таковой для треугольной фигуры. Это совпадение не является случайным, поскольку боковые грани обеих пирамид – это равнобедренные треугольники.
Задача на определение бокового ребра пирамиды Хеопса

Каждый человек знает, что первое чудо света – пирамида Хеопса, обладает головокружительными размерами. Она является самой большой из всех пирамид, находящихся в египетской Гизе. Стороны ее основания образуют квадрат с точностью до нескольких десятков сантиметров. Средняя длина стороны пирамиды оценивается в 230,363 метра. Высота пирамиды в настоящее время составляет около 137 метров, однако исходная высота каменного гиганта была 146,50 метров.
Воспользуемся приведенными выше цифрами, чтобы определить, чему равно боковое ребро правильной пирамиды четырехугольной, посвященной фараону Хеопсу.
Поскольку нам известна высота h и длина стороны a монумента, то следует применить такую формулу для b:
Подставляя в нее известные данные, получаем, что боковое ребро правильной четырехугольной пирамиды равно 273 метра, что немногим меньше периметра футбольного поля (300 метров).
Формулы и свойства правильной треугольной пирамиды. Усеченная треугольная пирамида
Объемной фигурой, которая часто появляется в геометрических задачах, является пирамида. Самая простая из всех фигур этого класса – треугольная. В данной статье разберем подробно основные формулы и свойства правильной пирамиды треугольной.
Геометрические представления о фигуре
Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.
Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.
 Вам будет интересно: Лихой – это: значение и синонимы
Вам будет интересно: Лихой – это: значение и синонимы
Она состоит из 4-х сторон, причем все они являются треугольниками. Точки, в которых соединяются три грани, называются вершинами. Их у фигуры также четыре. Линии пересечения двух граней – это ребра. Ребер у рассматриваемой пирамиды 6. Рисунок ниже демонстрирует пример этой фигуры.

Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.
Правильная пирамида
Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.
Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.
Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.
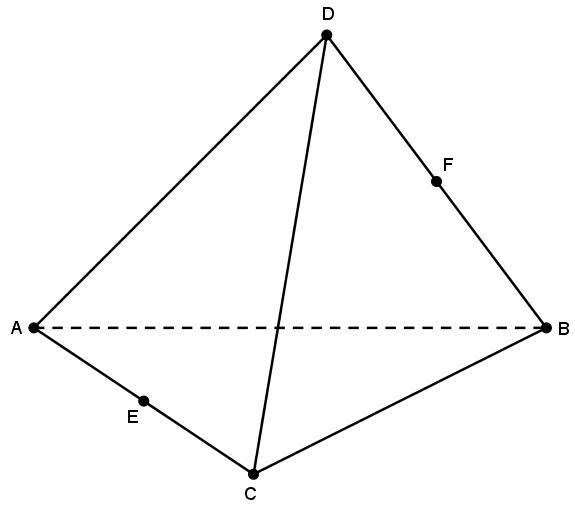
Сторона основания, высота, боковое ребро и апотема
Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.
Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.
Для высоты h получаем выражение:
Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.
Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:
Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.
Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.
Объем фигуры
Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:
Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:
Где высота правильной треугольной пирамиды равна h, а ее сторона основания – a.
Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:
То есть он определяется длиной стороны a однозначно.
Площадь поверхности
Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.
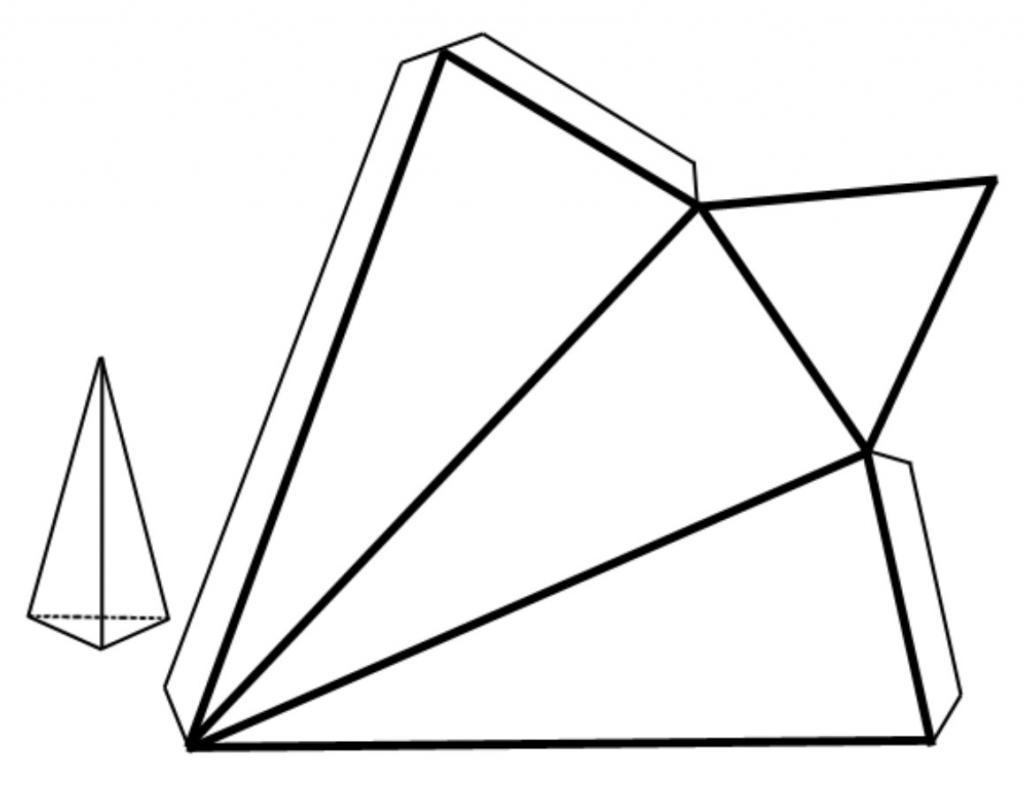
Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:
Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.
Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:
Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.
Полная площадь поверхности фигуры равна:
S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a
Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:
Свойства правильной усеченной пирамиды треугольной
Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.
В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.
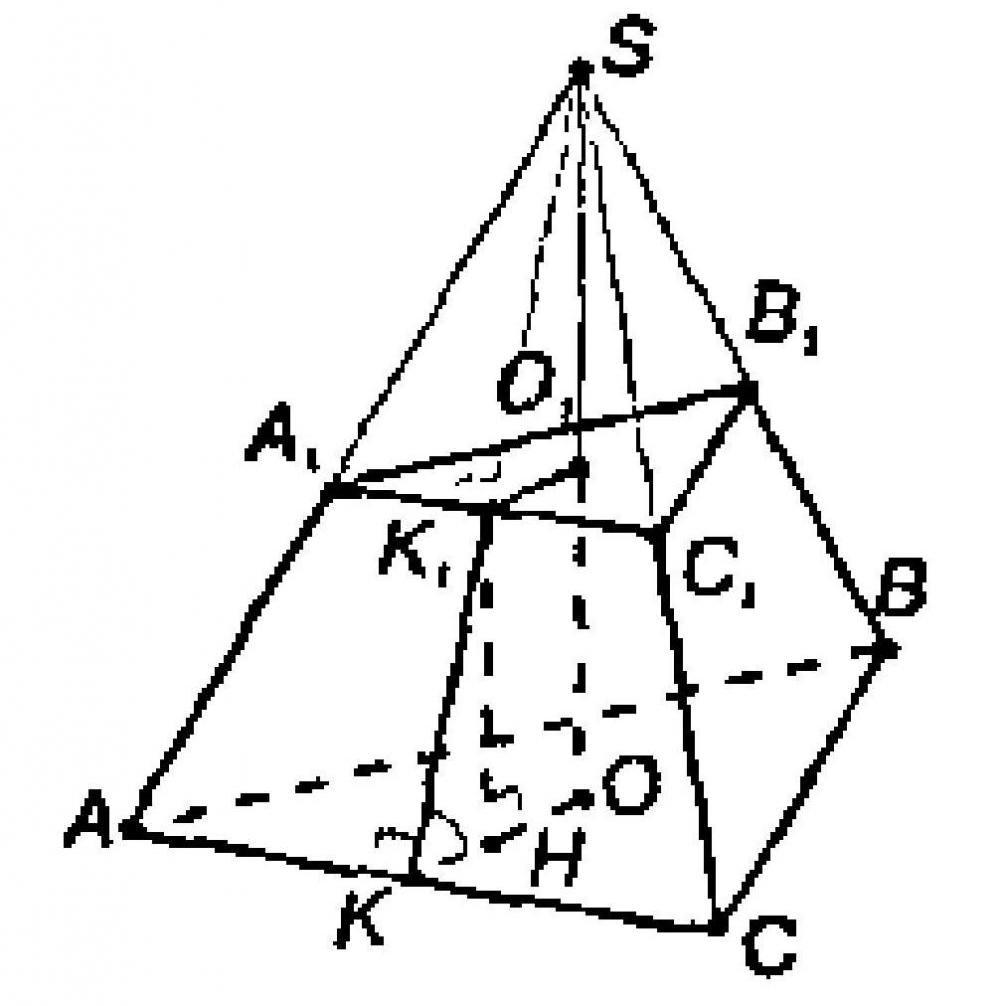
Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.
Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:
S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)
Здесь первое слагаемое – это площадь боковой поверхности, второе слагаемое – площадь треугольных оснований.
Объем фигуры рассчитывается следующим образом:
V = √3/12*h*(a12 + a22 + a1*a2)
Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.
Геометрические фигуры. Правильная пирамида.
Правильная пирамида – когда основанием пирамиды является правильный многоугольник, а высота проецируется в центр основания (или проходит через него).
В правильной пирамиде все боковые ребра имеют одинаковую величину, и каждая боковая грань является равнобедренными треугольниками одного размера.

Правильная пирамида обладает следующими свойствами:
Формулы для правильной пирамиды.
V – объем пирамиды,
S – площадь основания пирамиды,
h – высота пирамиды,
Sb – площадь боковой поверхности пирамиды,
a – апофема (не путать с α) пирамиды,
P – периметр основания пирамиды,
n – число сторон основания пирамиды,
b – длина бокового ребра пирамиды,
α – плоский угол при вершине пирамиды.
Ниже указанная формула определения объема используется лишь для правильной пирамиды:

V – объем правильной пирамиды,
h – высота правильной пирамиды,
n – количество сторон правильного многоугольника, основания правильной пирамиды,
a – длина стороны правильного многоугольника.
Боковое ребро правильной пирамиды находят по формуле:

где b — боковое ребро правильной пирамиды (SA, SB, SC, SD либо SE),
n — количество сторон правильного многоугольника (основание правильной пирамиды),
a — сторона правильного многоугольника (AB, BC, CD, DE либо EA) – основания правильной пирамиды,
h — высота правильной пирамиды (OS).
Указания к решению задач. Свойства, которые мы перечислили выше, помогают при практическом решении. Когда нужно определить углы наклона граней, их поверхность и так далее, значит общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для определения отдельных элементов пирамиды, так как большинство элементов оказываются общими для нескольких фигур.
Нужно разбить всю объемную фигуру на отдельные элементы – треугольники, квадраты, отрезки. Дальше, к отдельным элементам применяем знания из курса планиметрии, что очень упрощает определение ответа.
Правильная треугольная пирамида.
Правильная треугольная пирамида – это пирамида, у которой основанием оказывается правильный треугольник, а вершина опускается в центр основания.

Формулы для правильной треугольной пирамиды.
Формула для нахождения объема правильной треугольной пирамиды:

V – объем правильной пирамиды, которая имеет в основании правильный (равносторонний) треугольник,
h – высота правильной пирамиды,
a – длина стороны основания правильной пирамиды.
Так как правильная треугольная пирамида – это частный случай правильной пирамиды, значит, формулы, верные для правильной пирамиды, оказываются верными и для правильной треугольной.
Еще одним частным случаем правильно пирамиды является тетраэдр.
[spoiler title=”источники:”]
http://1ku.ru/obrazovanie/41519-formuly-i-svojstva-pravilnoj-treugolnoj-piramidy-usechennaja-treugolnaja-piramida/
http://www.calc.ru/Geometricheskiye-Figury-Pravilnaya-Piramida.html
[/spoiler]

{V= S cdot h}
На этой странице собраны формулы и калькуляторы для нахождения объема пирамиды. Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
Содержание:
- калькулятор объема пирамиды
- формула объема пирамиды
- объем правильной треугольной пирамиды
- объем правильной четырехугольной пирамиды
- объем правильной шестиугольной пирамиды
- объем правильной n-угольной пирамиды
- объем тетраэдра
- примеры задач
Формула объема пирамиды
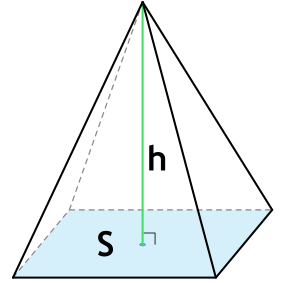
{V= dfrac{1}{3} S cdot h}
S – площадь основания пирамиды
h – высота пирамиды
Формула объема правильной треугольной пирамиды
Правильная треугольная пирамида – пирамида, в основании которой лежит равносторонний треугольник, а грани являются равнобедренными треугольниками.
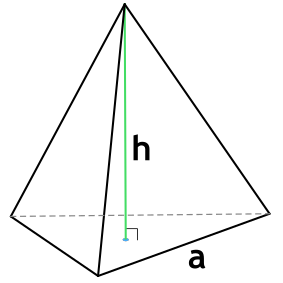
{V= dfrac{h cdot a^2}{4 sqrt{3}}}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной четырехугольной пирамиды
Правильная четырехугольная пирамида – пирамида, в основании которой лежит квадрат, а грани являются равнобедренными треугольниками.
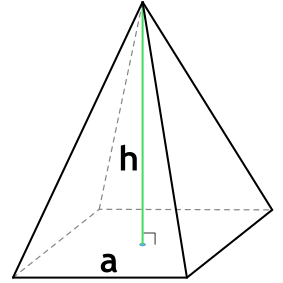
{V= dfrac{1}{3} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной шестиугольной пирамиды
Правильная шестиугольная пирамида – пирамида, в основании которой лежит правильный шестиугольник, а грани являются равнобедренными треугольниками.
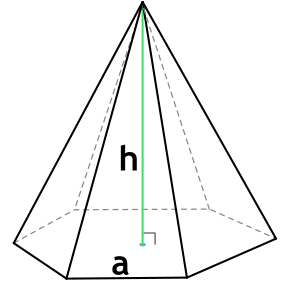
{V= dfrac{sqrt{3}}{2} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной n-угольной пирамиды
Правильная пирамида имеет в основании правильный многоугольник (все стороны и углы равны между собой), а высота проходит через центр этого основания.

{V= dfrac{n cdot h cdot a^2}{12 cdot tg(dfrac{180°}{n} )}}
a – длина стороны основания пирамиды
h – высота пирамиды
n – число сторон многоугольника в основании пирамиды
Формула объема тетраэдра
Тетраэдр – правильный многогранник (четырехгранник), имеющий четыре грани, каждая из которых является правильным треугольником. У тетраэдра кроме четырех граней также 4 вершины и 6 ребер.
{V= dfrac{sqrt{2} a^3}{12}}
a – длина стороны тетраэдра
Примеры задач на нахождение объема пирамиды
Задача 1
Найдите объем пирамиды с высотой 2м, а основанием ее служит квадрат со стороной 3м.
Решение
Так как в основании пирамиды лежит квадрат, то воспользуемся формулой объема правильной четырехугольной пирамиды и подставим в нее значения высоты и стороны основания.
V= dfrac{1}{3} cdot h cdot a^2 = dfrac{1}{3} cdot 2 cdot 3^2 = dfrac{1}{3} cdot 2 cdot 9 = dfrac{1}{3} cdot 18 = 6 : м^3
Ответ: 6 м³
Используем калькулятор для проверки полученного ответа.
Задача 2
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1см, а высота равна √3см.
Решение
Из условия следует, что пирамида правильная треугольная. Это значит, что для решения задачи необходимо воспользоваться формулой для правильной треугольной пирамиды. Подставим в нее значения и рассчитаем объем.
V= dfrac{h cdot a^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1}{4 sqrt{3}} = dfrac{sqrt{3}}{4 sqrt{3}} = dfrac{cancel{sqrt{3}}}{4 cancel{sqrt{3}}} = dfrac{1}{4} = 0.25 : м^3
Ответ: 0.25 см³
Для проверки с помощью калькулятора извлечем квадратный корень из 3: √3 = 1.73205. Теперь можем подставить значения в калькулятор и проверить полученный ответ.
