План урока
- Усечённая пирамида
Цели урока
- Знать, какая фигура называется усечённой пирамидой;
- Знать, какая усечённая пирамида называется правильной;
- Знать и уметь доказывать теорему о площади боковой поверхности усечённой пирамиды.
Разминка
- Что такое пирамида?
- Какую пирамидой называют правильной?
- Какую фигуру на плоскости называют трапецией?
- Что называют расстоянием между плоскостями?
Усечённая пирамида
Определение 1
Усечённая пирамида
— часть пирамиды, заключенная между её основанием, боковыми гранями и сечением этой пирамиды плоскостью, параллельной основанию.
На рисунке 1 изображена пирамида SA1A2A3…An, основание которой лежит в плоскости α. Плоскость β, параллельная плоскости α, пересекает боковые рёбра пирамиды в точках B1, B2, B3, …, Bn и разбивает пирамиду на два многогранника. Один из многогранников заключён между основанием A1A2A3…An, боковыми гранями исходной пирамиды и многоугольником B1B2B3…Bn.
Этот многогранник является усечённой пирамидой и обозначается A1A2A3…AnB1B2B3…Bn.
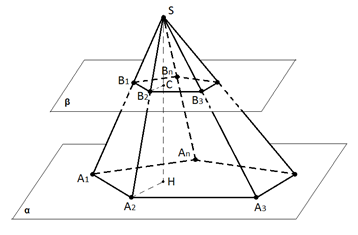
Рис. 1. Усечённая пирамида A1A2A3…AnB1B2B3…Bn
Многоугольники A1A2A3…An и B1B2B3…Bn называются основаниями усечённой пирамиды.
Многоугольники A1A2B2B1, A2A3B3B2, …, AnA1B1Bn называются боковыми гранями усечённой пирамиды.
Отрезки A1B1, A2B2, …, AnBn называются боковыми рёбрами усечённой пирамиды.
На рисунке также показана высота SH исходной пирамиды и высота CH усечённой пирамиды.
Определение 2
Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется
высотой усечённой пирамиды
.
Боковые грани усечённой пирамиды являются трапециями. Докажем, например, что боковая грань A1A2B2B1 – трапеция (рис. 1). Стороны A1A2 и B1B2 параллельны, так как лежат на прямых, по которым плоскость SA1A2 пересекается с параллельными плоскостями α и β. Другие две стороны A1B1 и A2B2 этой грани не параллельны, поскольку прямые, которым принадлежат эти стороны, пересекаются в точке S. Таким образом, в четырёхугольнике A1A2B2B1 две противоположные стороны параллельны, а две другие стороны не параллельны. Значит, A1A2B2B1 – трапеция. Аналогично доказывается, что и остальные грани – трапеции.
Введём понятие правильной усечённой пирамиды.
Определение 3
Правильной усеченной пирамидой
называется усеченная пирамида, полученная сечением правильной пирамиды плоскостью, параллельной основанию.
Основания усечённой пирамиды – правильные многоугольники, а боковые грани – равные между собой равнобедренные трапеции. Высоты этих трапеций называются
апофемами
.
Теорема 1
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
Доказательство
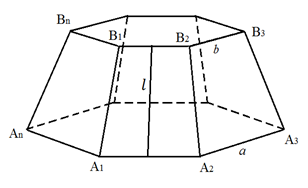
Рис. 2. К доказательству теоремы 1
Боковые грани правильной усечённой пирамиды – равные между собой равнобедренные трапеции с одним и тем же верхним основанием a, нижним b и высотой (апофемой) l (рис. 2). Поэтому площадь одной грани равна 12·(a+b)·l. Площадь всех граней, т.е. боковая поверхность, равна 12·(an+bn)·l, где
n – число вершин у основания пирамиды, an и bn – периметры оснований пирамиды.
Теорема доказана.
Пример 1
Высота правильной четырёхугольной усечённой пирамиды равна 7 см. Стороны оснований равны 10 см и 2 см. Найдите боковое ребро пирамиды.
Решение
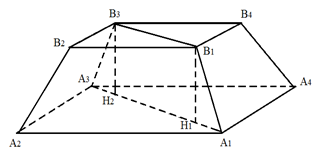
Рис. 3. К примеру 1
Пусть квадраты A1A2A3A4 и B1B2B3B4 являются основаниями правильной четырёхугольной усечённой пирамиды (рис. 3).
По условию A1A2=10 см, B1B2=2 см.
Диагональное сечение этой призмы A1A3B3B1 является равнобедренной трапецией с основаниями A1A3 и B1B3.
Найдём эти основания.
A1A3=A2A32+A1A22=102+102=200=102,
B1B3=B2B32+B1B22=22+22=8=22.
По условию высота пирамиды равна 7 см. Значит, в прямоугольном треугольнике A1B1H1 катет B1H1 равен 7 см. Найдём катет A1H1.
A1H1=A1A3-B1B32=102-222=42.
Найдём теперь боковое ребро усечённой пирамиды A1B1, которое является гипотенузой прямоугольного треугольника A1B1H1.
A1B1=A1H12+B1H12=422+72=32+49=81=9 см.
Ответ: 9 см.
Пример 2
Стороны оснований правильной усечённой треугольной пирамиды 4 дм и 1 дм. Боковое ребро 2 дм. Найдите высоту пирамиды.
Решение
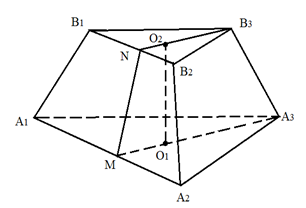
Рис. 4. К примеру 2
Центры оснований O1 и O2 правильной треугольной пирамиды A1A2A3B1B2B3 (рис. 4) делят медианы оснований A3M и B3N в отношении 2:1 считая от вершин A3 и B3. Отрезок O1O2 является высотой пирамиды.
Найдём сначала медианы равносторонних треугольников A1A2A3 и B1B2B3 (они также являются и высотами этих треугольников).
A3M=A2A32-A2M2=42-22=16-4=12=23 дм;
B3N=B2B32-B2N2=12-122=1-14=34=32 дм.
Теперь найдём отрезки A3O1 и B3O2.
A3O1=23·A3M=23·23=433 дм;
B3O2=23·B3N=23·32=33 дм.
Рассмотрим прямоугольную трапецию O1A3B3O2. Проведём высоту B3H.
B3H=O1O2.
A3H=A3O1-B3O2=433-33=3 дм.
По условию A3B3=2 дм.
Тогда по теореме Пифагора получим
B3H=A3B32-A3H2=22-32=4-3=1 дм.
Таким образом, мы нашли высоту усечённой пирамиды O1O2=1 дм.
Ответ: 1 дм.
Упражнение 1
1. В правильной усеченной четырёхугольной пирамиде высота равна 2 см, а стороны оснований 3 см и 5 см. Найдите диагональ этой пирамиды.
2. Стороны оснований усечённой правильной треугольной пирамиды 2 см и 6 см. Боковая грань образует с большим основанием угол 60o. Найдите высоту.
3. Высота правильной четырёхугольной усечённой пирамиды равна 4 см. Стороны оснований равны 2 см и 8 см. Найдите площади диагональных сечений.
4. В правильной четырёхугольной усечённой пирамиде стороны оснований 8 м и 2 м. Высота пирамиды равна 4 м. Найдите площадь полной поверхности.
Контрольные вопросы
- Сформулируйте определение усечённой пирамиды.
- Какая усечённая пирамида называется правильной?
- Сформулируйте и докажите теорему о площади боковой поверхности правильной усечённой пирамиды.
Ответы
Упражнение 1
- 6 см;
- 2 см;
- 202 см2;
- 168 м2.
Зная стороны оснований усеченной пирамиды, можно вычислить внутренний угол оснований, представленных правильными многоугольниками, периметры и площади оснований усеченной пирамиды, а также радиусы вписанной и описанной около оснований окружностей, воспользовавшись формулами для правильных многоугольников.
γ=180°(n-2)/n
P=n(a+b+d)
S_a=(na^2)/(4 tan〖(180°)/n〗 )
S_b=(nb^2)/(4 tan〖(180°)/n〗 )
r_a=a/(2 tan〖(180°)/n〗 )
r_b=b/(2 tan〖(180°)/n〗 )
R_a=a/(2 sin〖(180°)/n〗 )
R_b=a/(2 sin〖(180°)/n〗 )
Боковое ребро усеченной пирамиды дает возможность рассчитать через трапеции во внутреннем и боковом пространстве пирамиды апофему и высоту, а также углы между ними и основаниями.
Чтобы найти апофему усеченной пирамиды, рассмотрим боковую грань, представляющую собой равнобедренную трапецию, разделенную апофемой на две конгруэнтные прямоугольные трапециями, основаниями которых являются половины сторон оснований самой пирамиды. Исходя из этого апофема равна по теореме Пифагора квадратному корню из разности квадрата бокового ребра и квадрата разности половин сторон оснований пирамиды. (рис. 50.2)
f=√(d^2-(b/2-a/2)^2 )=√(d^2-(b-a)^2/4)
Чтобы найти высоту усеченной пирамиды, рассмотрим трапецию во внутреннем пространстве тела, между высотой и боковым ребром. Основаниями такой трапеции служат половины радиусов описанных окружностей вокруг оснований усеченной пирамиды. Следовательно, формула высоты по аналогии с апофемой выглядит следующим образом. (рис. 50.3)
h=√(d^2-(R_b-R_a )^2 )
Чтобы рассчитать углы при основаниях усеченной пирамиды и боковом ребре, можно воспользоваться в этой же трапеции/прямоугольном треугольнике тригонометрическими отношениями и принципом суммы углов трапеции.
cosδ=(R_b-R_a)/d
ε=180°-δ
Углы при основаниях и апофеме усеченной пирамиды можно вычислить в трапеции, которую апофема образует с высотой пирамиды подобным образом, через радиусы вписанных в основания окружностей. (рис. 50.4)
cosβ=(r_b-r_a)/f
α=180°-β
Площадь боковой поверхности усеченной пирамиды состоит из n-ного количества равнобоких трапеций, площадь каждой из которых равна произведению полусуммы оснований трапеции на ее высоту, то есть, перекладывая на измерения пирамиды – полусуммы сторон оснований пирамиды на ее апофему. Чтобы найти площадь полной поверхности, нужно прибавить к полученному значению обе площади оснований усеченной пирамиды.
S_(б.п.)=nf (a+b)/2
S_(п.п.)=S_(б.п.)+S_(осн.1,2)=n(f (a+b)/2+a^2/(4 tan〖(180°)/n〗 )+b^2/(4 tan〖(180°)/n〗 ))
Объем усеченной пирамиды, зная стороны оснований и боковое ребро, можно найти через высоту и площади оснований, найденные по указанным выше формулам.
V=1/3 h(S_осн1+S_осн2+√(S_осн1 S_осн2 ))
Материал урока.
На прошлых уроках
мы работали с пирамидами. Давайте вспомним, какой многогранник называется
пирамидой, что такое правильная пирамида, вспомним свойства правильной пирамиды.
Многогранник, составленный из -угольника и
треугольников, называется пирамидой.
Пирамида называется правильной,
если ее основание – правильный многоугольник.
Площадь боковой поверхности правильной
пирамиды равна половине произведения периметра основания на апофему.
Все боковые ребра правильной пирамиды
равны, а боковые грани являются равными равнобедренными треугольниками.
Пусть нам дана
пирамида PA1A2…An. Проведем секущую плоскость β,
параллельную плоскости основания пирамиды и пусть эта плоскость пересекает
боковые ребра в точках B1,B2,…,
Bn.
Плоскость β
разбивает пирамиду на две фигуры: пирамиду PB1B2…Bn и многогранник. Многогранник, гранями которого являются n-угольники A1A2…An и B1B2…Bn, расположенные в параллельных плоскостях и n четырехугольников A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называется
усеченной пирамидой.
Вокруг нас много
примеров усеченных пирамид. Вытяжка над кухонной плитой имеет форму усеченной
пирамиды.клавиши клавиатуры и другие предметы.
N-угольники
A1A2…An и B1B2…Bn называются соответственно верхним и нижним основанием.
Четырехугольники A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называются боковыми
гранями.
Отрезки A1B1,…, AnBn называются боковыми рёбрами
усеченной пирамиды.
Усеченную пирамиду
обозначают так A1A2…AnB1B2…Bn. Возьмем на верхнем основании произвольную
точку C и из этой точки опустим перпендикуляр на нижнее
основание. Этот перпендикуляр называется высотой усеченной пирамиды.
Теперь давайте
докажем, что боковые грани усеченной пирамиды – это трапеции.
Для доказательства
рассмотрим грань A1A2B2B1. Понятно,
что для других боковых граней доказательство будет проводится аналогично.
Поскольку секущая
плоскость проводилась параллельно плоскости основания, то можно записать, что A1A2
параллельно B1B2.
Очевидно, что две другие стороны четырехугольника A1A2B2B1 не параллельны (они пересекаются в точке P). Получаем, что этот четырехугольник – трапеция. Очевидно,
что все остальные боковые грани тоже будут трапециями.
Как и в случае с
пирамидой, усеченная пирамида тоже может быть правильной.
Усеченная пирамида
называется правильной, если она получена сечением правильной пирамиды
плоскостью, параллельной основанию.
Основаниями
усеченной пирамиды являются правильные многоугольники, а боковые грани –
равнобедренные трапеции.
Высоты этих трапеций
называются апофемами.
Объединение боковых граней называется боковой
поверхностью усеченной пирамиды, а объединение всех граней называется полной
поверхностью усеченной пирамиды. Тогда площадью боковой поверхности
пирамиды называется сумма площадей ее боковых граней.
А площадью полной поверхности пирамиды называется
сумма площадей всех ее граней.
Теперь давайте
сформулируем и докажем теорему о площади боковой поверхности правильной
усеченной пирамиды.
Площадь боковой
поверхности правильной усеченной пирамиды равна произведению полусуммы
периметров основания на апофему.
Доказательство.
Запишем формулу для
нахождения площади боковой поверхности усеченной пирамиды.
Поскольку усеченная
пирамида правильная, значит, ее гранями будут равнобедренные трапеции.
Площадь равнобедренной
трапеции равна произведению полусуммы оснований на высоту. Высота боковой грани
есть ничто иное как апофема усеченной пирамиды.
Подставим все в
исходную формулу, вынесем половину апофемы за скобки, а в скобках сгруппируем
стороны по основаниям. Тогда получим, что площадь боковой поверхности будет
равна произведению полусуммы периметров оснований усеченной пирамиды на
апофему.
Что и
требовалось доказать.
Решим несколько
задач.
Задача. Стороны
оснований правильной усеченной четырехугольной пирамиды равны
и
. Высота пирамиды
равна . Найти площадь
боковой поверхности.
Решение.
Ответ. 120
см2
Решим еще одну
задачу.
Задача. Пирамида
пересечена плоскостью, параллельной основанию. Доказать что боковые ребра и
высота пирамиды делятся этой плоскостью на пропорциональные части.
Решение.
Что и
требовалось доказать.
Решим еще одну
задачу.
Задача. Правильная
треугольная пирамида с высотой
и стороной основания
равной рассечена плоскостью
, проходящей через
середину высоты
параллельно
основанию . Найти площадь
боковой поверхности полученной усеченной пирамиды.
Решение.
Ответ.
135 см2.
Подведем итоги
урока. Сегодня на уроке мы познакомились с такими понятиями как усеченная
пирамида, правильная усеченная пирамида. Рассмотрели свойства правильной
усеченной пирамиды. Решили несколько задач.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
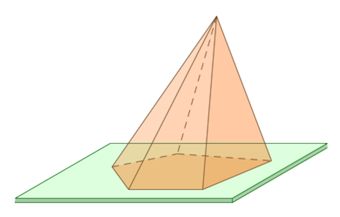
По числу углов основания различают пирамиды треугольные, четырехугольные и т. д.
Вершина пирамиды – точка, соединяющая боковые ребра и не лежащая в плоскости основания.
Основание – многоугольник, которому не принадлежит вершина пирамиды.
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины. В правильной пирамиде длина апофемы выражается формулой (m = sqrt {{b^2} – largefrac{{{a^2}}}{4}normalsize}).
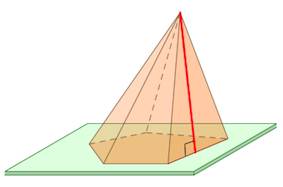
Высота – отрезок перпендикуляра, проведенного через вершину пирамиды к плоскости ее основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра). В правильной пирамиде высота равна (h = largefrac{{sqrt {4{b^2}{{sin }^2}frac{pi }{n} – {a^2}} }}{{2sin frac{pi }{n}}}normalsize), где (b) − боковое ребро, (a) − сторона основания, (n) − число сторон многоугольника в основании.
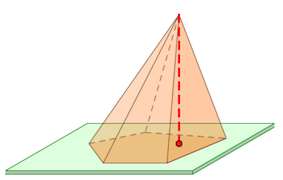
Диагональное сечение пирамиды – сечение пирамиды, проходящее через вершину и диагональ основания.
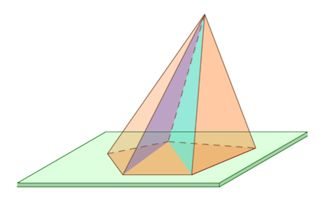
Некоторые свойства пирамиды
1. Если все боковые ребра равны, то около основания пирамиды можно описать окружность, причем вершина пирамиды проецируется в ее центр.
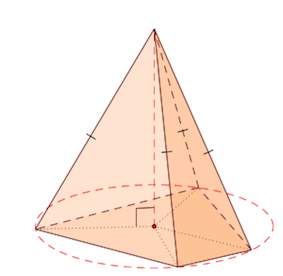
Боковые ребра образуют с плоскостью основания равные углы.
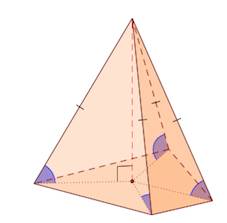
Верно и обратное.
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причем вершина пирамиды проецируется в ее центр, то все боковые ребра пирамиды равны.
2. Если все грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, причем вершина пирамиды проецируется в ее центр.
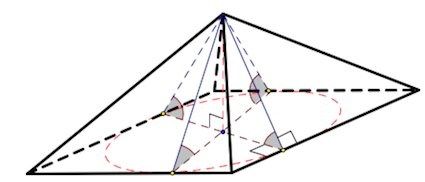
Виды пирамид
Пирамида называется правильной, если основанием ее является правильный многоугольник, а вершина проецируется в центр основания.
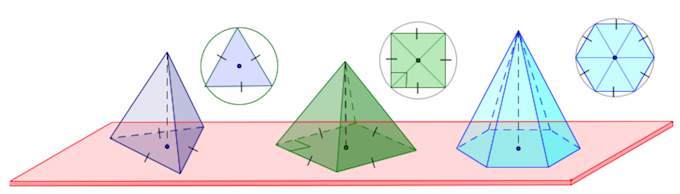
Для правильной пирамиды справедливо:
- боковые ребра правильной пирамиды равны;
- в правильной пирамиде все боковые грани – равные равнобедренные треугольники;
- в любую правильную пирамиду можно вписать сферу;
- около любой правильной пирамиды можно описать сферу;
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Пирамида называется прямоугольной, если одно из боковых ребер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.
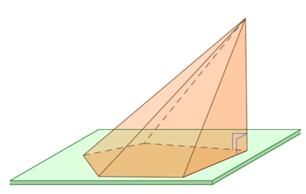
Усеченной пирамидой называется многогранник, заключенный между основанием пирамиды и секущей плоскостью, параллельной ее основанию.
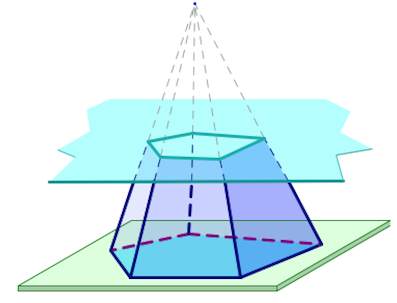
Усеченная пирамида является правильной, если она представляет собой часть правильной пирамиды.
Свойства усеченной пирамиды:
- Каждая боковая грань правильной усеченной пирамиды является равнобокими трапециями одной величины.
- Основания усеченной пирамиды являются подобными многоугольниками.
- Боковые ребра правильной усеченной пирамиды имеют равную величину и один наклонен по отношению к основанию пирамиды.
- Боковые грани усеченной пирамиды являются трапециями.
- Двугранные углы при боковых ребрах правильной усеченной пирамиды имеют равную величину.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
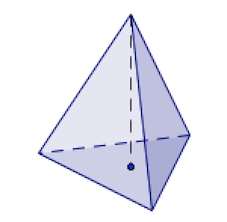
В правильном тетраэдре все четыре грани являются равносторонними треугольниками.
Соотношение между длиной ребра и высотой в правильном тетраэдре: (h = asqrt {largefrac{2}{3}}normalsize).
