1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании
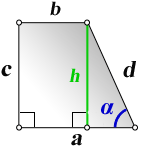
a – нижнее основание
b – верхнее основание
d – боковая сторона
α – угол при нижнем основании
h – высота трапеции
c – боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с) :

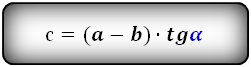
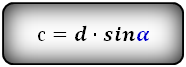
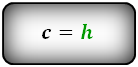
2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
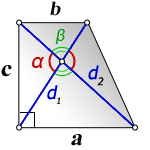
a – нижнее основание
b – верхнее основание
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
c – боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с):
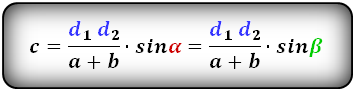
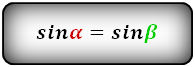
3. Формулы боковой стороны (с) прямоугольной трапеции через площадь
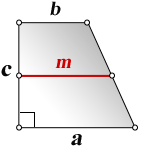
a – нижнее основание
b – верхнее основание
m – средняя линия трапеции
c – боковая сторона под прямым углом к основаниям
Формула длины боковой стороны (с) :
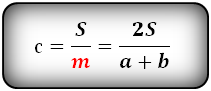
4. Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
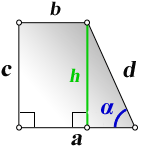
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
α – угол при нижнем основании
h – высота трапеции
d – боковая сторона
Формулы длины боковой стороны (d) :

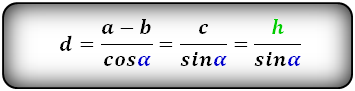
5. Формула боковой стороны (d) прямоугольной трапеции через площадь
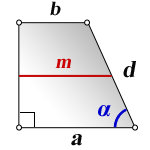
a – нижнее основание
b – верхнее основание
m – средняя линия трапеции
α – угол при нижнем основании
d – боковая сторона
Формула длины боковой стороны (d) :
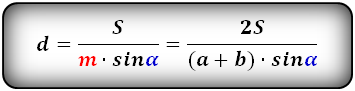
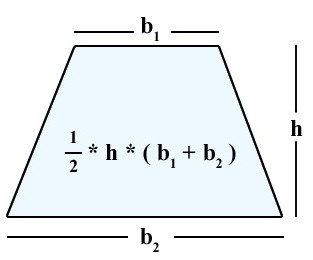
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 17 октября 2013
-
Обновлено: 13 августа 2021

Как найти боковую сторону трапеции
Геометрия – наука, которую начинают изучать еще в школе. Ошибочно думать, что она никак не пригодится в жизни. Иногда необходимы точные размеры фигур, чтобы сделать, к примеру, WEB-дизайн помещения. А фигуры встречаются разные, в том числе и трапеции. Часто надо найти значения их боковых сторон или основания. Давайте в подробностях рассмотрим, как найти боковую сторону данного четырехугольника различной формы, если известны его углы, основания, диагонали, площадь и т.п.
1
Как найти боковую сторону трапеции, если известны основания?
Трапеция – это четырёхугольник, у которого параллельны лишь две стороны. И эти не пересекающиеся отрезки называются основаниями данной фигуры. Трапеции бывают различных вариантов:
- Равнобокие – это те, у которых боковые стороны равны.
- Прямоугольные – имеют у основания один прямой угол.
- Остроугольные, разносторонние – с двумя острыми углами у основания.
- Тупоугольные, разносторонние – с одним тупым углом у основания.
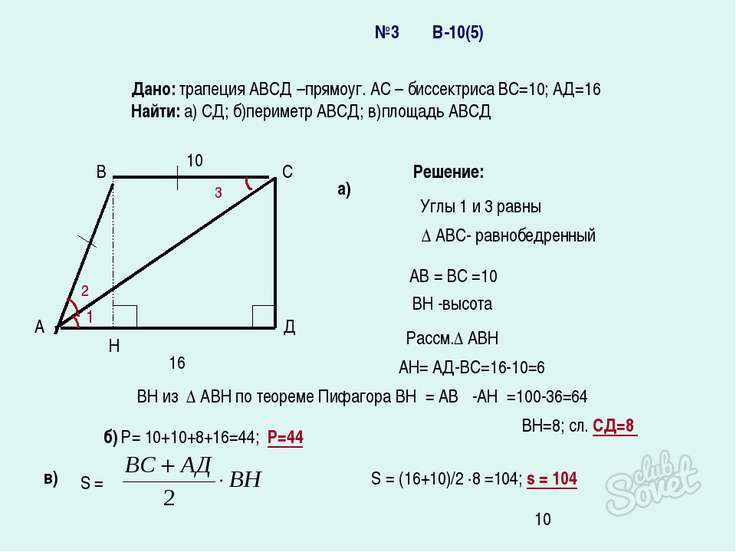
Рассмотрим вариант нахождения боковой стороны (высоты) прямоугольной трапеции, если вам даны значения оснований.
Чтобы решить данную задачу, вам понадобится сделать следующее:
- Проведите вторую высоту – ВН в четырехугольнике.
- Получившийся отрезок ВН = СД, так как основание ВС параллельно АД.
- Образовавшийся треугольник АВС – равнобедренный, ведь АС – биссектриса, соответственно углы у основания равны и АВ = СВ = 10 см.
- Рассмотрим треугольник АВН, фактически у нас известны две стороны его: ВА и АН. АН = АД – CD = 16 – 10 = 6 см.
- Отсюда по теореме Пифагора: ВН² = АВ² – НА² = 64; ВН = 8 см, соответственно и СД тоже равно 8 сантиметров.
Кроме того, если вам известен угол ВАД, то СД = (АД – ВС) • tg α либо СД = АВ • sin α.
Большая боковая сторона рассчитывается по следующим формулам:
- АВ² = СД² + (АД – ВС)²
- АВ = (АД – ВС)/cos ∠ВАН
- АВ = CД/sin ∠ВАН
2
Как найти боковую сторону прямоугольной трапеции, если известны диагонали, площадь, средняя линия?
Если обозначить высоту трапеции – b, большую боковую сторону – c, основания – a и к, диагонали – d1 и d2. Больший угол между ними β, меньший – α, то высоту (боковую сторону трапеции) можно найти по следующим формулам:
b = d2 • d1/ (a + к) • sin α;
или же b = d2 • d1/ (a + к) • sin β
Для того чтоб определить b – меньшую сторону прямоугольной трапеции, с – большую сторону фигуры, с известными данными S – площадью, n – средней линией, применяйте следующие расчеты:
b = S/n = 2S/ (a + к)
с = S/n • sin α = 2S/ (a + к) • sin α

3
Как найти боковые стороны равнобедренной трапеции?
Итак, у равнобокой трапеции АВ = DC. Если вам даны различные величины, то боковые стороны можно найти по нижеприведенным формулам:
- если известны высота – h и угол – α, то АВ = DC = h/ sin α;
- если даны значения оснований и угол – α , то АВ = DC = (a – b)/ cos α;
- если даны диагонали d и основания, то АВ² = DC² = d² – b • a;
- если известны значения средней линии – l, площадь – S, углы – α либо – β (вверху возле основания b, то АВ = DC = S/ l • sin α = S/ l • sin α.
или же:
АВ = DC = S/ (b + a) • sin α = S/ (b + a) • sin β
В дальнейшем, если вы выучите формулы и научитесь верно рисовать чертежи данных фигур, то решить задачку по геометрии вам не составит труда. Ведь по правильной картинке ответ задачи практически виден сразу.
Как найти боковую сторону прямоугольной трапеции
У каждой трапеции имеются две боковые стороны и два основания. Для того, чтобы узнать площадь, периметр или другие параметры этой фигуры, нужно знать хотя бы одну из боковых сторон. Также нередко по условиям задач требуется находить боковую сторону прямоугольной трапеции.

Инструкция
Начертите прямоугольную трапецию ABCD. Боковые стороны этой фигуры обозначьте, соответственно, как AB и DC. Первая боковая сторона DC совпадает с высотой трапеции. Она перпендикулярна двум основаниям прямоугольной трапеции.
Существует несколько способов нахождения боковых сторон. Так например, если в задаче дана вторая боковая сторона BA и угол ABH=60, то первую высоту найдите наиболее простым из способов, проведя высоту BH:
BH=AB*sinα
Поскольку BH=CD, то СD=AB*sinα=√3AB/2
Если, наоборот, дана сторона трапеции, обозначенная, как CD, а требуется найти ее же сторону AB, такая задача решается несколько иным образом. Так как BH=CD, и при этом, BH представляет собой катет треугольника ABH, можно сделать вывод, что сторона AB равна:
AB=BH/sinα=2BH/√3
Задачу можно решить и в том случае, если значения углов неизвестны, при условии, что даны два основания и боковая сторона AB. Однако, в этом случае можно найти только сторону CD, которая является высотой трапеции. Первоначально, зная значения оснований, найдите длину отрезка AH. Он равен разности большего и меньшего оснований, поскольку известно, что BH=CD:
AH=AD-BC
Затем, используя теорему Пифагора, найдите высоту BH, равную стороне CD:
BH=√AB^2-AH^2
Если у прямоугольной трапеции есть диагональ BD и угол 2α, как показано на рисунке 2, то сторону AB можно найти также по теореме Пифагора. Для этого, сначала вычислите длину основания AD:
AD=BD*cos2α
Затем найдите сторону AB следующим образом:
AB=√BD^2-AD^2
После этого докажите подобие треугольников ABD и BCD. Так как у этих треугольников одна общая сторона – диагональ, и при этом, два угла равны, как видно из рисунка, то эти фигуры подобны. На основании этого доказательства найдите вторую боковую сторону. Если известно верхнее основание и диагональ, то сторону найдите обычным образом с использованием стандартной теоремы косинусов:
c^2=а^2+b^2-2ab cos α, где а, b, с – стороны треугольника, α – угол между сторонами а и b.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
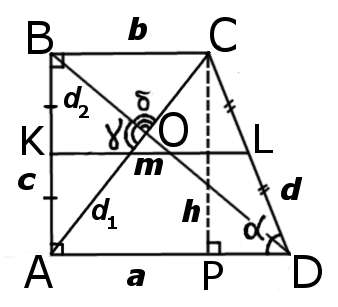
Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции
Определение.
Прямоугольная трапеция — это трапеция у котрой одна из боковых стороны перпендикулярна основам.
 |
| Рис.1 |
Признаки прямоугольной трапеции
Трапеция будет прямоугольной если выполняется одно из этих условий:
1. В тапеции есть два смежных прямых угла:
∠BAD = 90° и ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
AB ┴ BC, AB ┴ AD
Основные свойства прямоугольной трапеции
1. В трапеции есть два смежных прямых угла:
∠BAD = ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
AB ┴ BC ┴ AD
3. Высота равна меньшей боковой стороне:
h = AB
Стороны прямоугольной трапеции
Формулы длин сторон прямоугольной трапеции:
1. Формулы длины оснований через стороны и угол при нижнем основании:
a = b + d cos α = b + c ctg α = b + √d 2 – c2
b = a – d cos α = a – c ctg α = a – √d 2 – c2
2. Формулы длины оснований через стороны, диагонали и угол между ними:
| a = | d1d2 | · sin γ – b = | d1d2 | · sin δ – b |
| c | c |
| b = | d1d2 | · sin γ – a = | d1d2 | · sin δ – a |
| c | c |
3. Формулы длины оснований трапеции через площадь и другие стороны:
| a = | 2S | – b b = | 2S | – a |
| c | c |
4. Формула боковой стороны через другие стороны и угол при нижнем основании:
c = √d 2 – (a – b)2 = (a – b) tg α = d sin α
5. Формулы боковой стороны через основы, диагонали и угол между ними:
| c = | d1d2 | · sin γ = | d1d2 | · sin δ |
| a + b | a + b |
6. Формулы боковой стороны через площадь, основы и угол при нижнем основании:
| d = | S | = | 2S |
| m sin α | (a + b) sin α |
7. Формула боковой стороны через другие стороны, высоту и угол при нижнем основании:
| d = | a – b | = | c | = | h | = √c2 + (a – b)2 |
| cos α | sin α | sin α |
Средняя линия прямоугольной трапеции
Формулы длины средней линии прямоугольной трапеции:
1. Формулы средней линии через основание, высоту (она же равна стороне c ) и угол α при нижнем основании:
| m = | a – h · | ctg α | = | b + h · | ctg α |
| 2 | 2 |
2. Формулы средней линии через основания и боковые стороны сторону:
| m = | a – | √d 2 – c2 | = | b + | √d 2 – c2 |
| 2 | 2 |
Задачи с трапецией не кажутся сложными в ряде фигур, которые изучены ранее. Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
Определение прямоугольной трапеции и ее свойства
У произвольной трапеции основания параллельны, а боковые стороны могут иметь произвольное значение углов к ним. Если рассматривается прямоугольная трапеция, то в ней одна из сторон всегда перпендикулярна основаниям. То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
Другие углы в прямоугольной трапеции − это всегда острый и тупой. Причем их сумма всегда будет равна 180 градусам.
Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Какие обозначения приняты в представленных формулах?
Все величины, используемые в разных выражениях, которые описывают трапецию, удобно сразу оговорить и представить в таблице:
| Величина | Ее обозначение |
| a | большее основание |
| b | меньшее основание прямоугольной трапеции |
| c, h | перпендикулярная к основаниям боковая сторона, высота |
| d | наклонная боковая сторона |
| α | острый угол |
| β | тупой угол |
| м | средняя линия трапеции |
| д1 | меньшая диагональ |
| д2 | большая диагональ |
Формулы, которые описывают элементы прямоугольной трапеции
Самая простая из них связывает высоту и меньшую боковую сторону:
c = h.
Еще несколько формул для этой стороны прямоугольной трапеции:
с = d *sinα;
c = (a – b) * tg α;
c = √ (d2 – (a – b)2).
Первая вытекает из прямоугольного треугольника. И говорит о том, что катет к гипотенузе дает синус противолежащего угла.
В том же треугольнике второй катет равен разности двух оснований. Поэтому справедливо утверждение, которое приравнивает тангенс угла к отношению катетов.
Из того же треугольника можно вывести формулу, основываясь на знании теоремы Пифагора. Это третье записанное выражение.
Можно записать формулы для другой боковой стороны. Их тоже три:
d = (a – b) /cosα;
d = c / sin α;
d = √ (c2 + (а – b)2).
Первые две опять получаются из соотношения сторон в том же прямоугольном треугольнике, а вторая выводится из теоремы Пифагора.
Какой формулой можно воспользоваться для расчета площади?
Той, что дана для произвольной трапеции. Только нужно учесть, что высотой является сторона, перпендикулярная к основаниям.
S = (a + b) * h / 2.
Эти величины не всегда даны явно. Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
Как быть, если нужно вычислить диагонали?
В этом случае нужно увидеть, что они образуют два прямоугольных треугольника. Значит, всегда можно воспользоваться теоремой Пифагора. Тогда первая диагональ будет выражаться так:
d1 = √ (с2 + b2)
или по-другому, заменив «с» на «h»:
d1 = √ (h2 + b2).
Аналогичным образом получаются формулы для второй диагонали:
d2 = √ (с2 + b2) или d2 = √ (h2 + а2).
Задача №1
Условие. Площадь прямоугольной трапеции известна и равна 120 дм2. Ее высота имеет длину 8 дм. Необходимо вычислить все стороны трапеции. Дополнительным условием является то, что одно основание меньше другого на 6 дм.
Решение. Поскольку дана прямоугольная трапеция, в которой известна высота, то сразу же можно сказать о том, что одна из сторон равна 8 дм, то есть меньшая боковая сторона.
Теперь можно сосчитать другую: d = √ (с2 + (а – b)2). Причем здесь сразу даны и сторона с, и разность оснований. Последнее равно 6 дм, это известно из условия. Тогда d будет равняться квадратному корню из (64 + 36), то есть из 100. Так найдена еще одна боковая сторона, равная 10 дм.
Сумму оснований можно найти из формулы для площади. Она будет равна удвоенному значению площади, разделенному на высоту. Если считать, то получается 240 / 8. Значит, сумма оснований — это 30 дм. С другой стороны, их разность равна 6 дм. Объединив эти уравнения, можно сосчитать оба основания:
а + b = 30 и а – b = 6.
Можно выразить а как (b + 6), подставить его в первое равенство. Тогда получится, что 2b будет равняться 24. Поэтому просто b окажется 12 дм.
Тогда последняя сторона а равна 18 дм.
Ответ. Стороны прямоугольной трапеции: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Задача №2
Условие. Дана прямоугольная трапеция. Ее большая боковая сторона равняется сумме оснований. Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Решение. Начать нужно с искомого. Нужная площадь определится как произведение a и b. Обе эти величины не известны.
Потребуется использовать дополнительные равенства. Одно из них построено на утверждении из условия: d = а + b. Необходимо воспользоваться третьей формулой для этой стороны, которая дана выше. Получится: d2 = с2 + (a – b)2 или (a + b)2 = с2 + (a – b)2.
Необходимо сделать преобразования, подставив вместо с его значение из условия – 12. После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
В начале решения шла речь о том, что а*b дает искомую площадь. Поэтому в последнем выражении можно заменить это произведение на S. Простой расчет даст значение площади. S = 36 см2.
Ответ. Искомая площадь 36 см2.
Задача №3
Условие. Площадь прямоугольной трапеции 150√3 см². Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Решение. Из свойства углов трапеции получается, что ее тупой угол равен 120º. Тогда диагональ делит его на равные, потому что одна его часть уже 60 градусов. Тогда и угол между этой диагональю и вторым основанием тоже 60 градусов. То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
Теперь нужно рассмотреть прямоугольный треугольник. В нем третий угол равен 30 градусам. Значит катет, лежащий против него, равен половине гипотенузы. То есть меньшее основание трапеции равно половине искомой диагонали: b = a/2. Из него же нужно найти высоту, равную боковой стороне, перпендикулярной основаниям. Сторона с здесь катет. Из теоремы Пифагора:
с = (a/2) * √3.
Теперь осталось только подставить все величины в формулу площади:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Решение этого уравнения дает корень 20
Ответ. Меньшая диагональ имеет длину 20 см.
