В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
-
Формула площади правильной пирамиды
- 1. Общая формула
-
2. Площадь правильной треугольной пирамиды
- 3. Площадь правильной четырехугольной пирамиды
- 4. Площадь правильной шестиугольной пирамиды
Формула площади правильной пирамиды
1. Общая формула
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Sполн. = Sбок. + Sосн.
Боковой гранью правильной пирамиды является равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
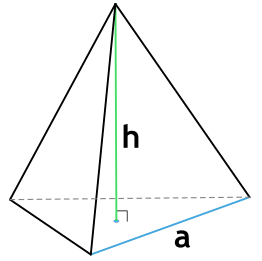
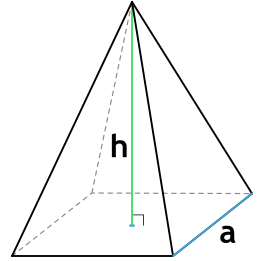
1. Через длину основания (a) и высоту (h):
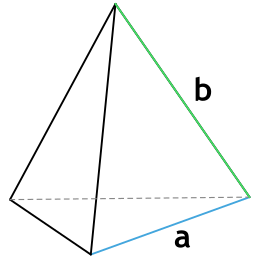
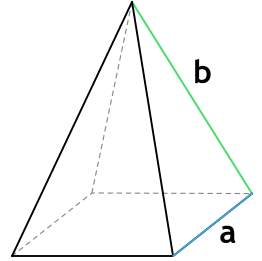
2. Через основание (a) и боковую сторону (b):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
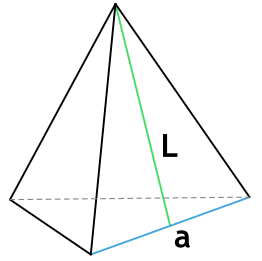
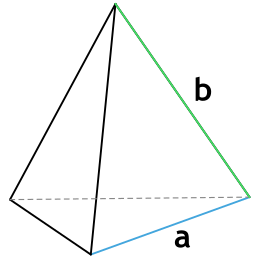
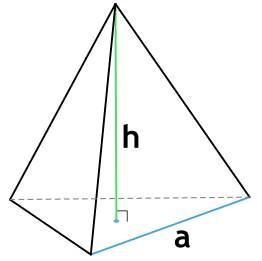
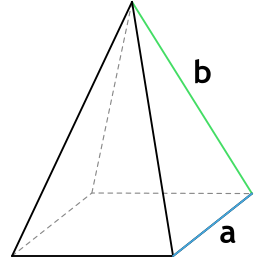
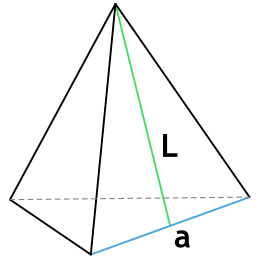
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
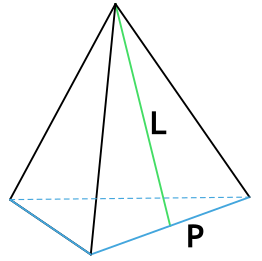
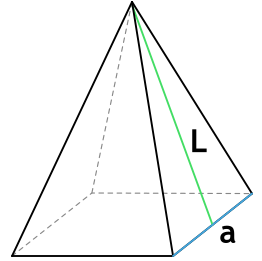
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.
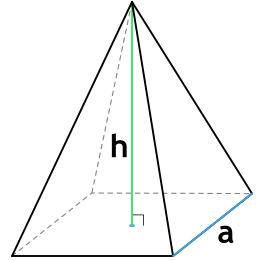
3. Площадь правильной четырехугольной пирамиды
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 2aL |
 |
|
| полная | Sполн. = a2 + 2aL |
 |
microexcel.ru
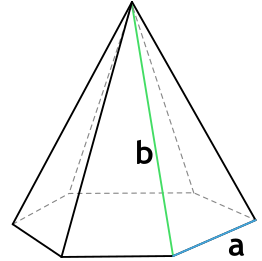
4. Площадь правильной шестиугольной пирамиды
Основание: правильный шестиугольник

{S_{полн} = dfrac{1}{2}PL + S}
На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды. Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.
- калькулятор площади поверхности пирамиды
- формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
- формула площади полной поверхности правильной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной пирамиды через периметр и апофему
- формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- примеры задач
Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.
Площадь полной поверхности пирамиды – это сумма площадей боковых граней и площади основания.
Площадь боковой поверхности пирамиды – это совокупная площадь всех боковых граней пирамиды.
Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.
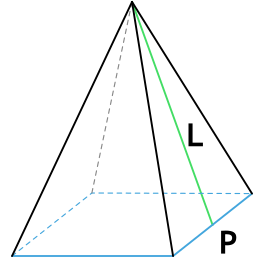
Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
{S_{полн} = dfrac{1}{2}PL+S}
P – периметр основания пирамиды
L – апофема пирамиды
S – площадь основания пирамиды
Формула площади полной поверхности правильной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{na}{2} {Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} + sqrt{h^2+ Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
n – число сторон основания
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{a^2 sqrt{3}+6aL}{4}}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{a^2 sqrt{3}+6a sqrt{b^2 – dfrac{a^2}{4}}}{4}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{3a}{2} {Bigg( dfrac{a}{2 tg ( 60°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{полн} = 2a {Bigg( dfrac{a}{2 tg ( 45°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{полн} = a^2+2aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3asqrt{b^2-dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{полн} = 3a {Bigg( dfrac{a}{2 tg ( 30°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади боковой поверхности правильной пирамиды через периметр и апофему
{S_{бок} = dfrac{1}{2}PL}
P – периметр основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{na}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( dfrac{180°}{n})} Bigg) ^2} }
a – сторона основания пирамиды
h – высота пирамиды
n – число сторон основания
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{бок} = dfrac{3}{2}aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{бок} = dfrac{3a sqrt{b^2 – dfrac{a^2}{4}}}{2}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{3a}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
{S_{бок} =dfrac{1}{2}PL}
P – периметр основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{бок} = 2aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 2a sqrt{b^2 – dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{бок} = 3aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 3asqrt{b^2-dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{бок} = 3a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Примеры задач на нахождение площади поверхности пирамиды
Задача 1
Стороны основания правильной четырехугольной пирамиды равны 60см, боковые ребра равны 78см. Найдите площадь поверхности этой пирамиды.
Решение
Так как пирамида правильная четырехугольная, то воспользуемся соответствующей формулой площади поверхности через сторону основания и боковую грань.
S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}} = 60^2 + 2 cdot 60 sqrt{78^2- dfrac{60^2}{4}} = 3600 + 120 sqrt{6084- dfrac{3600}{4}} = 3600 + 120 sqrt{6084 – 900} = 3600 + 120 sqrt{5184} = 3600 + 120 cdot 72 = 3600 + 8640 = 12240 : см²
Ответ: 12240 см²
Проверим полученный ответ с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной треугольной пирамиды со стороной 6см и апофемой 10см.
Решение
Из условия мы знаем апофему и сторону правильной треугольной пирамиды, поэтому нам потребуется эта формула.
S_{бок} = dfrac{3}{2}aL = dfrac{3}{2} cdot 6 cdot 10 = dfrac{3}{2} cdot 60 = 90 : см²
Ответ: 90 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной четырехугольной пирамиды сторона основания 6см и высота 4см.
Решение
Подставим значения в формулу и произведем расчет.
S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} = 2 cdot 6 sqrt{4^2+ Bigg( dfrac{6}{2 tg ( 45°)} Bigg) ^2} = 60 : см²
Ответ: 60 см²
Проверка .
Пирамида, в основании которой лежит правильный шестиугольник, а боковые стороны образуются правильными треугольниками, называется шестиугольной.
Этот многогранник отличается множеством свойств:
- Все стороны и углы основания равны между собой;
- Все ребра и двугранные угля пирамиды также равны между собой;
- Треугольники, образующие боковые стороны одинаковы, соответственно, у них одинаковые площади, стороны и высоты.
Для расчета площади правильной шестиугольной пирамиды применяется стандартная формула площади боковой поверхности шестиугольной пирамиды:
где P – периметр основания, a – длина апофемы пирамиды. В большинстве случаев можно рассчитать боковую площадь по этой формуле, однако иногда можно воспользоваться и другим методом. Так как боковые грани пирамиды образованы равными треугольниками, можно найти площадь одного треугольника, а потом умножить его на количество боковых сторон. В шестиугольной пирамиде их 6. Но этот способ можно применять и при расчете площади треугольной пирамиды.Рассмотрим пример расчета площади боковой поверхности шестиугольной пирамиды.
Пусть дана правильная шестиугольная пирамида, в которой апофема равна a = 7 см, сторона основания b = 3 см. Рассчитайте площадь боковой поверхности многогранника.
Для начала найдем периметр основания. Так как пирамида правильная – в ее основании лежит правильный шестиугольник. Значит, все его стороны равны, а периметр рассчитывается по формуле:
Подставляем данные в формулу:
Теперь можем легко найти площадь боковой поверхности, подставив найденное значение в основную формулу:
Также немаловажным моментом является поиск площади основания. Формула площади основания шестиугольной пирамиды выводится из свойств правильного шестиугольника:
Рассмотрим пример расчета площади основания шестиугольной пирамиды, взяв за основу условия из прошлого примера.Из них мы знаем, что сторона основания b = 3 см. Подставим данные в формулу:
Формула площади шестиугольной пирамиды представляет собой сумму площади основания и боковой развертки:
Рассмотрим пример расчета площади шестиугольной пирамиды.
Пусть дана пирамида, в основании которой лежит правильный шестиугольник со стороной b = 4 см. Апофема заданного многогранника равна a = 6 см. Найдите полную площадь.
Мы знаем, что полная площадь состоит из площадей основания и боковой развертки. Поэтому для начала найдем их. Рассчитаем периметр:
Теперь найдем площадь боковой поверхности:
Далее рассчитываем площадь основания, в котором лежит правильный шестиугольник:
Теперь можем сложить получившиеся результаты:

Обозначения
- $SABCDEF$ — правильная шестиугольная пирамида
- $O$ — центр основания пирамиды
- $a$ — длина стороны основания пирамиды
- $h$ — длина бокового ребра пирамиды
- $S_{text{осн.}}$ — площадь основания пирамиды
- $V_{text{пирамиды}}$ — объем пирамиды
Площадь основания пирамиды
В основаниях пирамиды находится правильный шестиугольник со стороной $a$. По свойствам правильного шестиугольника, площадь основания пирамиды равна $$ S_{text{осн.}}=frac{3sqrt{3}}{2}cdot a^2 $$
Правильный шестиугольник в основании пирамиды

Находим $SO$
Прямая $SO$ является высотой пирамиды, поэтому $angle SOF=90^{circ}$. Треугольник $SOF$ прямоугольный, в нем $FO=a, FS=h$. По свойствам прямоугольного треугольника $$ SO=sqrt{FS^2-FO^2}=sqrt{h^2-a^2} $$
Объем пирамиды
Объем пирамиды вычисляется как треть произведения площади ее основания на ее высоту. Высотой правильной пирамиды является отрезок $SO$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{text{пирамиды}}=frac{1}{3}cdot S_{text{осн.}}cdot SO=frac{sqrt{3}}{2}cdot a^2 cdot sqrt{h^2-a^2} $$
Находим $ST$ и $TO$

Все что нужно знать о шестиугольной пирамиде
Пирамида – это трехмерная фигура, основание которой представляет собой многоугольник, а боковые стороны являются треугольниками. Шестиугольная пирамида – ее частный вид. Помимо того, существуют другие вариации, когда в основании треугольника (такая фигура называется тетраэдр) находится квадрат, прямоугольник, пятиугольник и так далее по нарастанию. Когда количество точек становится бесконечным, то получается конус.
Шестиугольная пирамида
В целом это одна из последних и самых сложных тем в стереометрии. Изучается где-то в 10-11 классах и рассматривается только вариант, когда в основании находится правильная фигура. Одно из труднейших заданий по ЕГЭ зачастую бывает связано с этим параграфом.

И-так, в основании правильной шестиугольной пирамиды лежит правильный шестиугольник. Что это значит? У фигуры в основании все стороны равны. Боковые же части состоят из равнобедренных треугольников. Вершины их соприкасаются в одной точке. Данная фигура представлена на фото ниже.
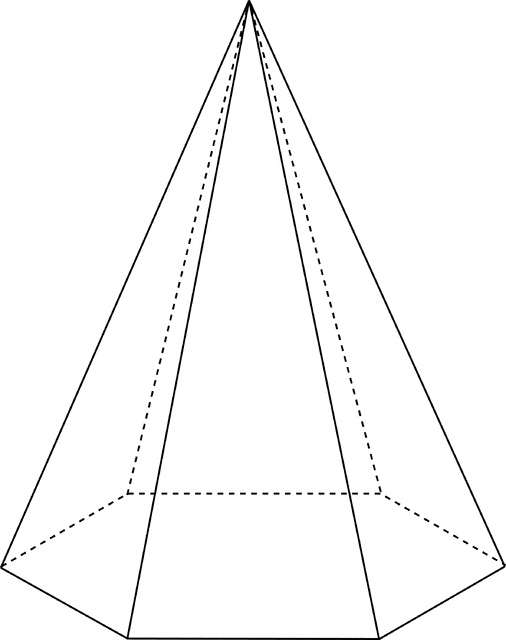
Как найти площадь всей поверхности и объем шестиугольной пирамиды?
В отличие от математики, которую преподают в университетах, школьная наука обучает обходить стороной и упрощать некоторые сложные понятия. Например, если не известно, как найти площадь фигуры, то приходится делить ее на части и уже по известным формулам площадей разделенных фигур находить ответ. Такому принципу нужно последовать и в представленном случае.
То есть, чтобы найти площадь поверхности всей шестиугольной пирамиды, надо найти площадь основания, затем площадь одной из боковых сторон и умножить ее на 6.
Применяются такие формулы:
S (полное) = 6S (боковой стороны) + S (основания) , (1);
S (основания) = 3√3 / 2a2 , (2);
6S (боковой стороны) = 6×1 / 2ab = 3ab , (3);
S (полное) = 3ab + (3√3 / 2a2) = 3(2a2b + √3) / 2a2 , (4).
Где S – площадь, см2;
a – длина основания, см;
b – апофема (высота боковой грани), см.
Для того чтобы найти площадь всей поверхности или какой-либо ее составляющей, требуется всего лишь сторона основания шестиугольной пирамиды и апофема. Если в задаче дано это в условии, то решение не должно составить труда.
С объемом дела обстоят намного легче, но чтобы его найти, нужна высота (h) самой шестиугольной пирамиды. Ну и, конечно же, сторона основания, благодаря которой нужно найти ее площадь.
Формула выглядит следующим образом:
V = 1/3 × S (основания) × h , (5).
Где V – объем, см3;
h – высота фигуры, см.

Вариант задачи, который может попасться на экзамене
Условие. Дана правильная шестиугольная пирамида. Длина основания равна 3 см. Высота составляет 5 см. Найти объем данной фигуры.
Решение: V = 1/3 × (3√3/2 × 32) × 5 = 5/3 × √3/6 = 5√3/18.
Ответ: объем правильной шестиугольной пирамиды составляет 5√3/18 см.
Автор:
25-09-2018 13:51
Жду ваши вопросы и мнения в комментариях