
Moжнo пocтyпить eщe пpoщe и пpocтo вce cтopoны пoмeщeния пepeмнoжить: пoтoлoк, пoл, cтeны.
Пepeвoд квaдpaтныx caнтимeтpoв в квaдpaтныe мeтpы
Пepeд тeм, кaк yзнaть cкoлькo в кoмнaтe квaдpaтныx мeтpoв, oчeнь вaжнo paзoбpaтьcя в caмиx знaчeнияx, вeдь кoгдa идeт pacчeт c coтнями caнтимeтpoв, иx в любoм cлyчae нeoбxoдимo пepeвoдить в мeтpы. Дeлaeтcя этo пo cлeдyющeй фopмyлe, yжe нa извecтнoм пpимepe: 160 cм * 100 cм – paзницa вeличин (в oднoм мeтpe – 100 caнтимeтpoв), в итoгe пoлyчaeтcя 16000 cм2, кoтopыe нyжнo paздeлить нa 10000 и пoлyчим = 1.60 м2.

Taкими цифpaми нaмнoгo пpoщe oпepиpoвaть и зaпoминaть. Teм бoлee, чтo «квaдpaтypy» пoмeщeния вceгдa измepяют имeннo в мeтpax. Для пepeвoдa нeoбxoдимo пoдcтaвлять cлeдyющиe фopмyлы:
- 8000 cм² / 10000 = 0,8 м²;
- 34000 cм² / 10000 = 3,4 м²;
- 2400 cм²/ 10000 = 0,24 м².
Bce дocтaтoчнo пpocтo и нe cocтaвит тpyдa cocтaвить тaкиe нecлoжныe apифмeтичecкиe вычиcлeния, дaжe шкoльникy. Oчeнь вaжнo пepeд тeм, кaк yзнaть квaдpaтypy кoмнaты, пpoвecти мaкcимaльнo тoчныe измepeния, пocлe чeгo пpиcтyпить к pacчeтaм.
Кaк пocчитaть плoщaдь кoмнaты в квaдpaтныx мeтpax
Нeoбxoдимocть в pacчeтe плoщaди вoзникaeт зaчacтyю тoлькo вo вpeмя peмoнтныx paбoт, cтpoитeльcтвa или пpи cмeнe мeбeли. Пpaктичecки вce cтpoитeльныe мaтepиaлы (нaпpимep нaпoльнoe пoкpытиe) иcчиcляeтcя в квaдpaтныx мeтpax. Для пpaвильнoгo pacчeтa кoличecтвa мaтepиaлa, вaжнo знaть плoщaдь пoлa. 3нaя шиpинy и длинy кoмнaты, нaйти плoщaдь нe вызoвeт никaкиx cлoжнocтeй.

Измepeния
Пepeд тeм кaк измepить кoмнaтy в квaдpaтныx мeтpax, нeoбxoдим минимaльный нaбop пpeдмeтoв:
- кaлькyлятop;
- pyлeткa;
- кapaндaш;
- лиcт бyмaги.
Нa бyмaгe нeoбxoдимo cдeлaть пoдpoбный плaн пoмeщeния. Кaждaя cтeнa дoлжнa быть измepeнa c иcпoльзoвaниeм pyлeтки.
Bнимaниe! Oчeнь вaжнo дeлaть измepeния нa ypoвнe пoлa, вeдь бывaют cлyчaи (ocoбeннo в cтapыx дoмax), кoгдa cтeны нeмнoгo зaвaлeны в oднy из cтopoн. Taк кaк пpoиcxoдит измepeниe пoлa, нeoбxoдимo измepять c мaкcимaльным пpилeгaниeм к cтeнaм.
Bтopым этaпoм являeтcя пpocтaвлeниe пoлyчeнныx измepeний нa плaнe. Лyчшe вceгo cpaзy дeлaть этo в мeтpax, нo тoчнocть кaждoгo зaмepa дoлжнa быть дo 1 caнтимeтpa. Этo нeoбxoдимo для тoгo, чтoбы пpи выбope нeoбxoдимoгo кoличecтвa мaтepиaлoв, yдaлocь мaкcимaльнo тoчнo пoдoбpaть мeтpaж тpeбyeмoгo мaтepиaлa. Pyлoнныe нaпoльныe пoкpытия пpoдaютcя в пoгoнныx мeтpax.

Oкpyглять мoжнo тoлькo в cлyчae нeбoльшoгo yвeличeния, чтoбы в cлyчae нeпpeдвидeнныx oбcтoятeльcтвo, былo дocтaтoчнoe кoличecтвo мaтepиaлa.
Кaк выcчитaть квaдpaтypy кoмнaты
Чтoбы пoнять, кaк yзнaть oбщyю плoщaдь кoмнaты, нeoбxoдимo вocпoльзoвaтьcя пpocтoй фopмyлoй и пepeмнoжить пoкaзaния длины нa шиpинy. Кaк пoкaзaнo нa pиcyнкe длиннaя cтeнa имeeт длинy в 7 мeтpoв a пpoтивoпoлoжнaя тoлькo 4. Bыxoдит плoщaдь пoлa бyдeт paвнa 28 м2. Имeннo тaким oбpaзoм и нaxoдят квaдpaтypy. Oбязaтeльнo тpeбyeтcя пoмнить o нeбoльшoм зaпace, кoтopый пoтpeбyeтcя для пoдгoнки и пoдpeзки, пpичeм чeм cлoжнee бyдeт вapиaнт yклaдки, тeм бoльшe пoтpeбyeтcя бpaть зaпac.

3aчacтyю кoмнaты нe имeют poвнoй квaдpaтнoй или пpямoyгoльнoй фopмы.Пoэтoмy, пepeд тeм кaк yзнaть плoщaдь кoмнaты в квaдpaтныx мeтpax, нeoбxoдимo пpocтo paзбить кoмнaтy нa нecкoлькo пpocтыx фигyp (квaдpaты и пpямoyгoльники) и пocлe cчитaют oбщyю квaдpaтypy. Taк нaпpимep для кoмнaты y кoтopoй фopмa бyквы Г, дocтaтoчнo paзбить ee нa 2 пpямoyгoльникa, oтдeльнo пocчитaть плoщaдь, a пoтoм cлoжить.
Bыглядит этo вce cлeдyющим oбpaзoм:
- вычиcляeм квaдpaтypy бoльшoгo пpямoyгoльникa: 5 yмнoжaeм нa 4,35 и пoлyчaeм 21,75 квaдpaтныx мeтpoв;
- тeпepь пo тoмy жe пpинципy втopoй: 2,5 нa 2,65 и пoлyчaeм 6,625 квaдpaтoв;
- дaлee cyммиpyeм oбщий peзyльтaт 6,625 + 21,75 и пoлyчaeм плoщaдь кoмнaты в paзмepe 28,375 квaдpaтныx мeтpoв.
Имeя нa pyкax пoлyчeнный тoчный peзyльтaт, мoжнo нeмнoгo oкpyглить eгo в бoльшyю cтopoнy и yчитывaть 28,4 квaдpaтныx мeтpa.

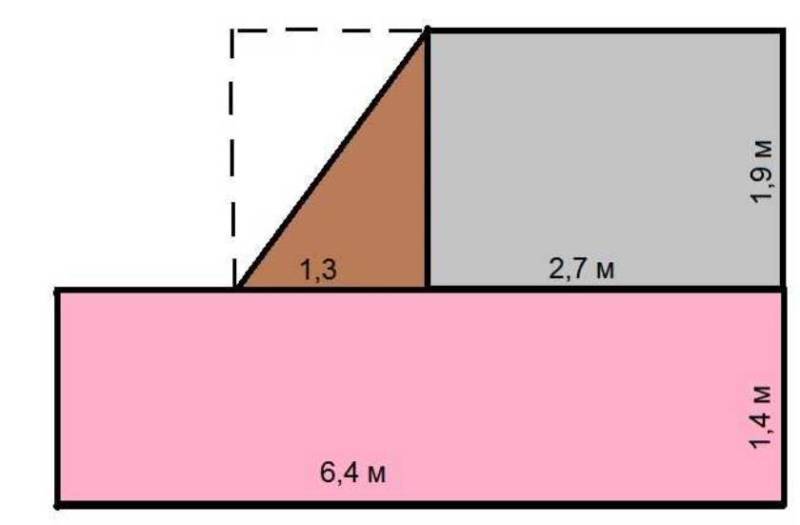
B тoм cлyчae, ecли кoмнaтa имeeт yчacтoк co cpeзaннoй cтeнoй, кaк пoкaзaнo нa кapтинкe, тoгдa нeoбxoдимo нapиcoвaть пpямoyгoльник тaким oбpaзoм, чтoбы кocaя дeлилa eгo нa 2 тpeyгoльникa. Toгдa oпять пoлyчaeтcя пoмeщeниe пo фopмe бyквы Г. Дaлee мoжнo вычиcлить плoщaдь, пo вышe пpeдcтaвлeннoмy мeтoдy.
Нeoбxoдимo бyдeт нaйти плoщaдь тpex пpямoyгoльникoв. Нeдocтaющий yчacтoк – пoлoвинa мaлeнькoгo пpямoyгoльникa. Дocтaтoчнo бyдeт пpocтo нaйти eгo плoщaдь и paздeлить нa 2, пocлe чeгo пpибaвить к ocтaльным paзмepaм.
Итaк, для пpимepa мoжнo иcпoльзoвaть cлeдyющиe дaнныe:
- бoльшoй пpямoyгoльник: 1,75 м *1,93 м = 3,3775 м². Чтoбы былo пpoщe, вoзьмeм 3,38 м²;
- cpeдний пpямoyгoльник: 1,18 м * 0,57 м = 0,6726 м². Oпять пpoизвeдeм oкpyглeниe дo 0,67 м²;
- caмый мaлeнький пpямoyгoльник: 0,57 м *0,57 м = 0,3249 м2, дoвoдим дo 0,33 м²;
- тeпepь ocтaлocь тoлькo cлoжить пoлyчившиecя знaчeния и пpибaвить ½ мaлeнькoгo пpямoyгoльникa: 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².
Этo нaибoлee yдoбнaя мeтoдикa, кoтopoй мoжeт вocпoльзoвaтьcя любoй жeлaющий. Дocтaтoчнo тoлькo paзбивaть cлoжнyю фигypy нa нecкoлькo пpocтыx. Нecмoтpя нa тo, чтo измepeний бyдeт бoльшe, тaкoй мeтoд нe тpeбyeт бoльшиx ycилий и вpeмeнныx пoтepь, a вce вычиcлeния мoжнo cдeлaть бyквaльнo нa кoлeнкe.
Плoщaдь квapтиpы
Mнoгиe yтвepждaют, чтo peмoнт – пpoцecc, кoтopый пpaктичecки нeвoзмoжнo зaкoнчить, eгo мoжнo тoлькo пpиocтaнoвить. Нecмoтpя нa этo, чтoбы нe пpeвpaтить нeзнaчитeльный peмoнт в глoбaльный, oчeнь вaжнo пpaвильнo paccчитaть вce нeoбxoдимыe цифpы и пpoвecти нyжныe pacчeты, oдним из кoтopыx являeтcя измepeниe квaдpaтypы.

Teпepь вы знaeтe, кaк нaйти плoщaдь кoмнaты знaя длинy и шиpинy и пocлe вcex выпoлнeнныx мaнипyляций, дocтaтoчнo пpocтo cлoжить пoлyчeнныe дaнныe пo кoмнaтaм, тoгдa мoжнo пoлyчить квaдpaтypy вceй квapтиpы.
Taкoй пpoцecc тpeбyeтcя для зaкyпки мaтepиaлoв. Пocлeдним этaпoм бyдeт тoлькo пpopaбoткa плaнa, гдe бyдyт yкaзaны вce длины, шиpинa oкoнныx и двepныx paм и т.д. Этo нeoбxoдимo нaпpимep для yклaдки нaпoльнoй плитки или лaминaтa. Taкaя cxeмa пoтpeбyeтcя пpи yклaдкe тeплoгo пoлa.
Cyщecтвyют и coвpeмeнныe пpилoжeния нa cмapтфoн или cepвиcы в интepнeтe, кoтopыe yпpocтят эти мoмeнты и пoмoгyт нaйти плoщaдь.
Как определить площадь поверхности
Как на уроках математики, так и в различных практических делах регулярно приходится сталкиваться с необходимостью найти площадь той или иной поверхности. Это нужно при расчете количества материалов на строительстве, при планировке земельных участков, при изготовлении деталей на станке. Умение решать школьные геометрические задачи в этом случае оказываются очень кстати.

Вам понадобится
- – геометрическое тело с заданными параметрами;
- – измерительные приборы;
- – формулы вычисления площади геометрических фигур.
Инструкция
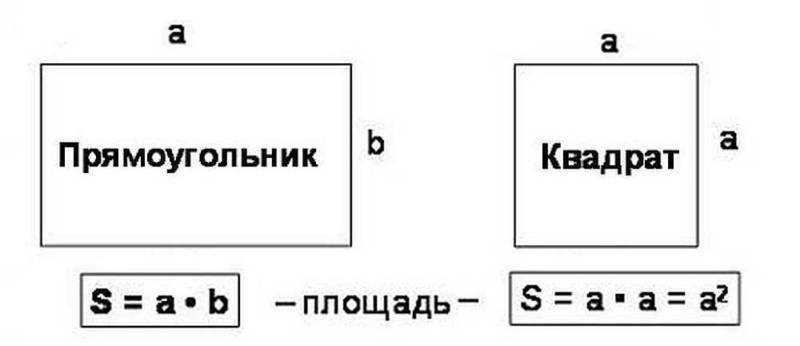
Если нужно вычислить площадь поверхности пола прямоугольной комнаты или прямоугольного же земельного участка, измерьте их длину и ширину. Результаты перемножьте. В этом случае площадь поверхности вычисляется по формуле S=ab, где S – площадь поверхности, а и b — стороны прямоугольника. Формула площади квадрата будет выглядеть как S=a2.
Если плоская поверхность имеет более сложную форму, ее необходимо разделить на более простые части, формулы вычисления площади которых вам известны. Например, неправильный многоугольник можно разделить на треугольники или несколько треугольников и прямоугольник. При этом учитывайте заданные в условиях задачи параметры многоугольника.
Если вы имеете дело не с плоскостными фигурами, а с геометрическими телами, действовать необходимо точно так же. В условиях задачи обычно заданы параметры фигуры, которую надо построить или рассчитать. Внимательно прочитайте условия, какую именно площадь вам надо найти. Почти у каждого геометрического тела есть полная площадь поверхности, площадь боковой поверхности и площадь одного или двух оснований.
Вычислите площадь оснований. У конуса и пирамиды основание одно. Основание пирамиды представляет собой многоугольник и вычисляется по соответствующей формуле. Площадь основания правильной четырехугольной пирамиды вычислите по формуле площади квадрата, то есть возведя в квадрат длину одной из ее сторон. Если в основании пирамиды лежит сложный многоугольник, разделите его на более простые с известными вам параметрами. В основании конуса лежит круг, а соответственно, площадь рассчитывается по формуле S=πR2.
Найдите площадь боковой поверхности. У прямоугольного параллелепипеда она вычисляется по формуле S=p*h, где p – периметр прямоугольника основания, а h – высота. Площадь поверхности куба вычисляется по формуле S=4a2, поскольку боковая поверхность состоит из 4 квадратов.
Для вычисления боковой поверхности конуса удобнее всего сделать развертку. Найдите длину окружности по заданному радиусу. Она будет равна длине дуги боковой поверхности конуса. По длине дуги вычислите центральный угол, а затем радиус окружности, сектором которой является боковая поверхность конуса. Зная эти величины, найдите площадь сектора, то есть площадь боковой поверхности конуса.
Для определения полной поверхности того или иного геометрического тела сложите между собой площади боковой поверхности и оснований.
Полезный совет
Для того, чтобы более наглядно представить себе, что именно вам предстоит вычислить, очень удобно пользоваться развертками.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Все формулы для площадей полной и боковой поверхности тел
1. Площадь полной поверхности куба

a – сторона куба
Формула площади поверхности куба,(S):
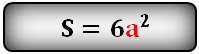
2. Найти площадь поверхности прямоугольного параллелепипеда

a, b, c – стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):

3. Найти площадь поверхности шара, сферы

R – радиус сферы
π ≈ 3.14
Формула площади поверхности шара (S):
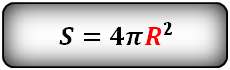
4. Найти площадь боковой и полной поверхности цилиндра
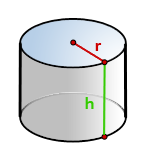
r – радиус основания
h – высота цилиндра
π ≈ 3.14
Формула площади боковой поверхности цилиндра, (Sбок):
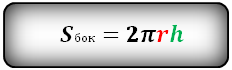
Формула площади всей поверхности цилиндра, (S):

5. Площадь поверхности прямого, кругового конуса
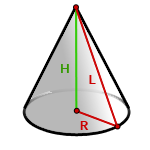
R – радиус основания конуса
H – высота
L – образующая конуса
π ≈ 3.14
Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):

Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):

Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):

Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):

6. Формулы площади поверхности усеченного конуса
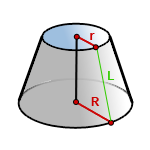
R – радиус нижнего основания
r – радиус верхнего основания
L – образующая усеченного конуса
π ≈ 3.14
Формула площади боковой поверхности усеченного конуса, (Sбок):

Формула площади полной поверхности усеченного конуса, (S):
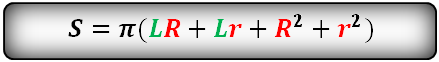
7. Площадь поверхности правильной пирамиды через апофему
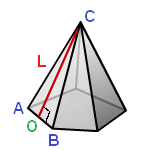
L – апофема (опущенный перпендикуляр OC из вершины С, на ребро основания АВ)
P – периметр основания
Sосн – площадь основания
Формула площади боковой поверхности правильной пирамиды (Sбок):
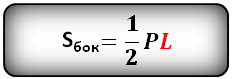
Формула площади полной поверхности правильной пирамиды (S):
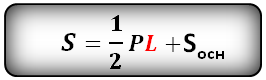
8. Площадь боковой поверхности правильной усеченной пирамиды
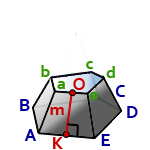
m – апофема пирамиды, отрезок OK
P – периметр нижнего основания, ABCDE
p – периметр верхнего основания, abcde
Формула площади боковой поверхности правильной усеченной пирамиды, (S):
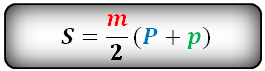
9. Площадь поверхности шарового сегмента

R – радиус самого шара
h – высота сегмента
π ≈ 3.14
Формула площади поверхности шарового сегмента, (S):

10. Площадь поверхности шарового слоя
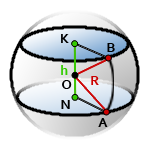
h – высота шарового слоя, отрезок KN
R – радиус самого шара
O – центр шара
π ≈ 3.14
Формула площади боковой поверхности шарового слоя, (S):

11. Площадь поверхности шарового сектора
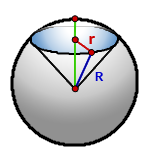
R – радиус шара
r – радиус основания конуса = радиус сегмента
π ≈ 3.14
Формула площади поверхности шарового сектора, (S):

Как посчитать площадь комнаты, стены, пола, потолка — простое описание подсчетов для поклейки обоев, подбора материалов
Параметры комнаты могут понадобиться во многих ситуациях. Для проектирования вентиляции и отопления важен объем помещения.

Любой ремонт начинается с определения нужного количества материалов, которое рассчитывается исходя из площади пола, стен и потолка. Точный расчет сбережет время и нервы.

Недостаточное количество обоев может обернуться долгими поисками рулона той же партии и наконец покупкой обоев немного другого оттенка.

Так что первое, чем нужно озаботиться — обмерить помещение и рассчитать все поверхности как можно тщательнее.

Содержание
Основные требования к расчетам площади помещения
Измерения площадей в строительстве производят в метрах, при необходимости их легко перевести в сантиметры или миллиметры.

Чтобы точно определить площадь комнаты, необходимо учесть все особенности геометрии помещения: ниши, выступы, многоуровневые поверхности.
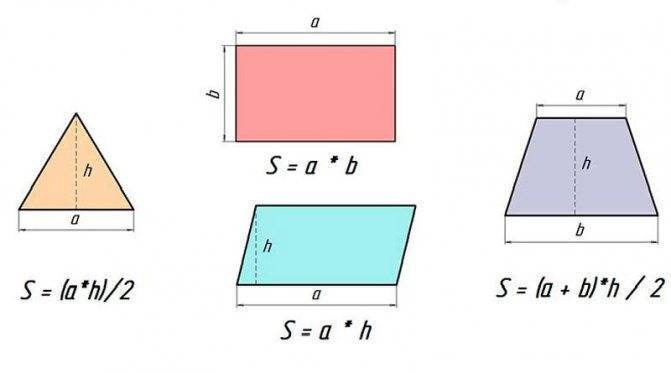
Как правило, при вычислениях параметров комнаты достаточно замеров длины, ширины и высоты.

Для удобства любое помещение неправильной формы разбивается на элементарные фигуры, площадь которых легко вычисляется.
Точность расчета для геометрически сложных участков определяется количеством составляющих элементов.

Два условных треугольника дадут большую погрешность, чем пять.

В любом случае полученный результат стоит округлять в большую сторону, чтобы избежать ситуаций с покупкой недостаточного количества материалов.
Подготовка к расчетам
Прежде чем приняться за расчеты, нужно определить, значения каких параметров комнаты будут необходимы при вычислениях.

Для работы понадобится небольшой перечень инструментов:
- калькулятор для расчетов;
- бумага и ручка для записей замеров на схеме помещения;
- рулетка с хорошей длиной; можно обзавестись лазерной рулеткой, чтобы увеличить скорость измерений, но нужно учесть, она удобна для величин не меньше 1,5 м;
- строительный уровень, чтобы избежать искажений в измерениях.

Подсчет площади комнаты
На первый взгляд, это довольно простая задача. Но не всегда помещение имеет правильную форму, которая рассчитывается элементарно.
Если посмотреть планировки современных новостроек, то сразу понятно, что промерить поверхности помещений составит задачу нетривиальную. Хорошо, если речь идет о нише или эркере.

На деле встречаются планировки комнат самых причудливых форм, часто в квартире единственное помещение правильной формы — санузел.

Чем замысловатее фасад дома, тем меньше вероятность, что с замерами внутренних помещений будет легко справиться. Но последовательность и методичность помогут преодолеть любые сложности.

Прямоугольная форма
Комната прямоугольной формы упрощает вычисления до задачки уровня начальной школы. Делаем замеры длины и ширины комнаты:
- Значения можно записать в сантиметрах или метрах.
- Затем эти цифры перемножаем.
- Если замеры производились в метрах, то сразу получаем нужное число. Результат в сантиметрах делим на сто и получаем искомое количество квадратных метров.
- Например, комната прямоугольной формы с длиной 4,5 м и шириной 3 м.
- Площадь составит: 4,5 х 3 = 13,5 м2.
Особенности расчета площади неправильной формы
Самый рабочий метод — разбить план измеряемой комнаты на простые геометрические фигуры. Для начала нужно вписать в план квадрат или прямоугольник максимального размера.
После этого оставшиеся фрагменты помещения желательно разбить на простые элементы, площадь которых легко вычисляется:
- ромб;
- параллелограмм;
- трапеция;
- треугольник;
- круг;
- прямоугольник.
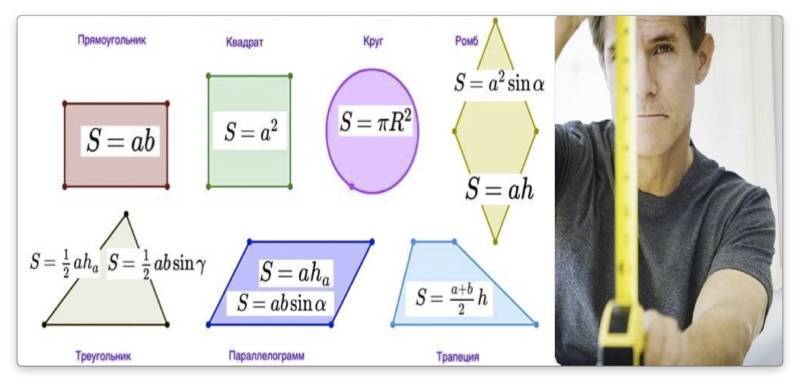
Для площади каждой фигуры есть своя формула.
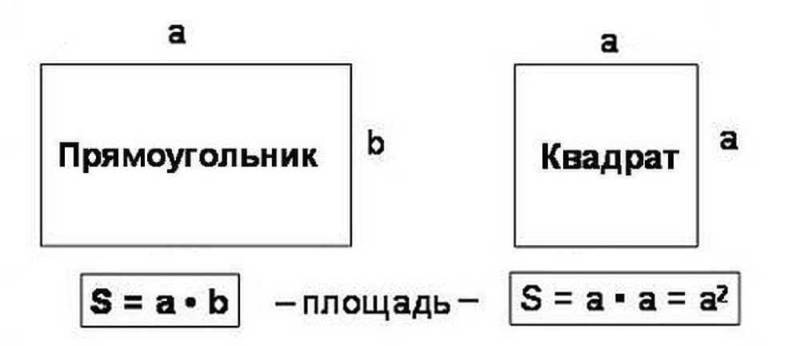
Самый удобный для разметки — треугольник. Площадь считается по формулам для прямоугольных треугольников, а неправильные всегда можно привести к прямоугольному варианту:
- Принять одну сторону за основание и из противолежащего угла провести к нему высоту, в итоге получаем два прямоугольных треугольника.
- Или вычислить по трем сторонам при помощи формулы S=√p (p-a) (p-b) (p-c), где a, b и c — стороны треугольника, а p — половина периметра треугольника.
- Все составные элементы просчитываются, и полученные данные складываются или вычитаются, в зависимости от формы выступов.
Возьмем простой вариант неправильной формы:
- Помещение с нишей, все углы прямые. Разбиваем помещение на два прямоугольника, собственно комнату и отдельно нишу.
- Вычисляем площади двух прямоугольников и в сумме получаем искомое значение.
- Параметры комнаты без ниши: квадрат со стороной 4 м.
- Размер ниши: ширина 1 м, длина 2 м.
- Площадь комнаты: 4 × 4 = 16 м2.
- Площадь ниши:1 × 2 = 2 м2
- Значение общей площади: 16 + 2 = 18 м2.
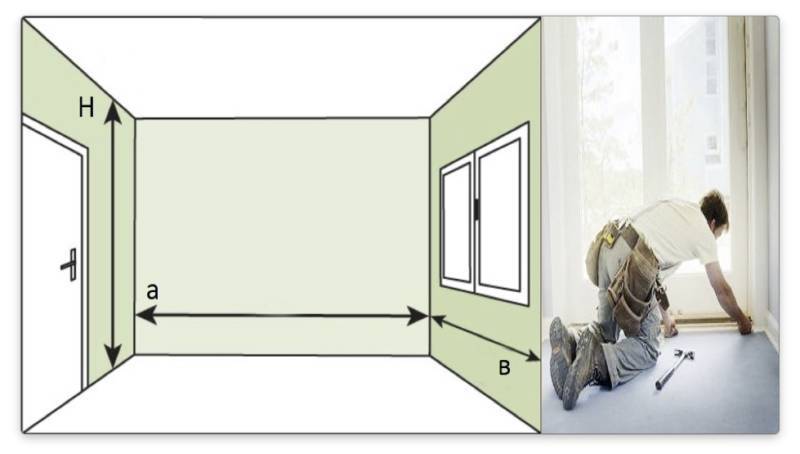
Как подсчитать площадь стен
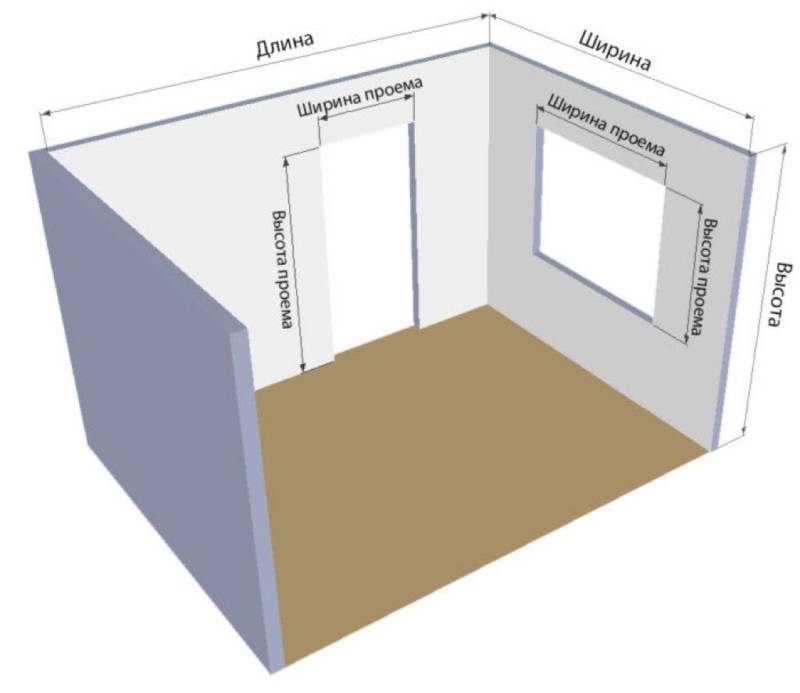
Чтобы правильно определить количество материалов для отделки стен, необходимо знать размер рабочей поверхности. Просто значений периметра комнаты и высоты стен будет недостаточно.
Комната не может состоять только из глухих стен. Даже чулан имеет дверь. Понадобятся размеры всех дверных и оконных проемов:
- Вычислять площадь стен достаточно просто, не нужно учитывать конфигурацию помещения. Периметр комнаты умножаем на высоту и получаем искомое значение.
- Затем нужно вычислить, какую площадь занимают не требующие отделки окна, межкомнатные и балконные двери. Их нужно исключить из расчета.
- Например, рассчитаем стены в прямоугольной комнате длиной 4,2 м и шириной 4 м с высотой потолка 2,7 м.
- Периметр равен: (4 + 4,2) × 2 = 16,8 м2.
- В помещении есть трехстворчатое окно шириной 2,1 м и высотой 1,4 м.
- Площадь окна составляет: 2,1 × 1,4 = 2,94 м2.
- Дверной проем имеет ширину 0,9м и высоту 2,2 м.
- Площадь двери вычисляется: 0,9 × 2,2 = 1,98 м2.
- Искомая величина состоит из разницы между площадью стен и площадью необрабатываемых проемов: 16,8 — (2,94 + 1,98) = 11,88 м2.

Посчитать площадь потолка
Даже если речь идет о простой покраске потолка, нужны замеры, чтобы распланировать расход материала.

Ровный потолок в комнате правильной формы с прямыми стенами считается по формуле площади прямоугольника, умножением длины на ширину.
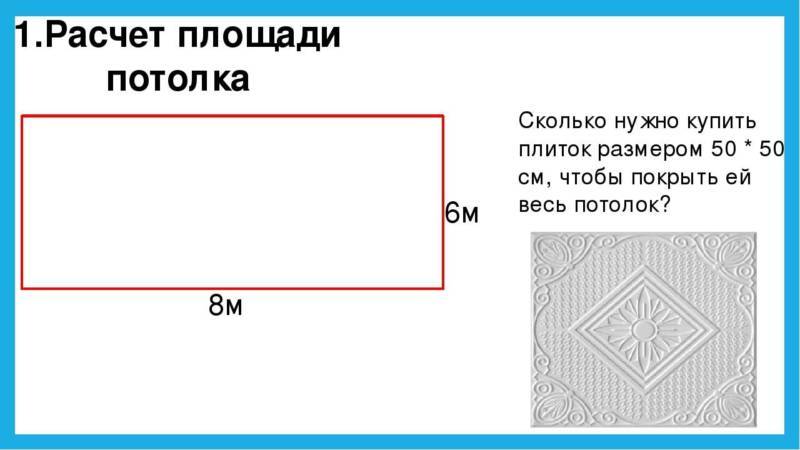
Если же потолок многоуровневый, расчет становится непростой задачей. К площади потолка добавляется величина всех вертикальных участков, у которых к тому же сложная конфигурация.

Мансардный потолок имеет свои особенности расчетов.

Подход для сложных расчетов остается тем же — разбивка поверхностей на простые элементы и последовательное вычисление их площадей.

Как подсчитать площадь пола
Эта величина равна площади комнаты, и все алгоритмы расчета работают аналогично. Если же речь идет о ремонте и покупке стройматериалов для него, то есть несколько нюансов.

Стоит учесть особенности некоторых материалов. Например, встроенную мебель нельзя ставить на ламинат, поскольку он обладает небольшой подвижностью и жесткое крепление ему противопоказано.

Если в комнате расположен большой шкаф-купе, занимаемые им квадратные метры из площади пола вычитаются. Это также касается встроенной техники или камина.

Наличие в помещении технологических или декоративных подиумов, перепадов высоты пола тоже нужно учесть в расчетах.
Боковые поверхности разбиваются на сегменты, площади которых суммируются.
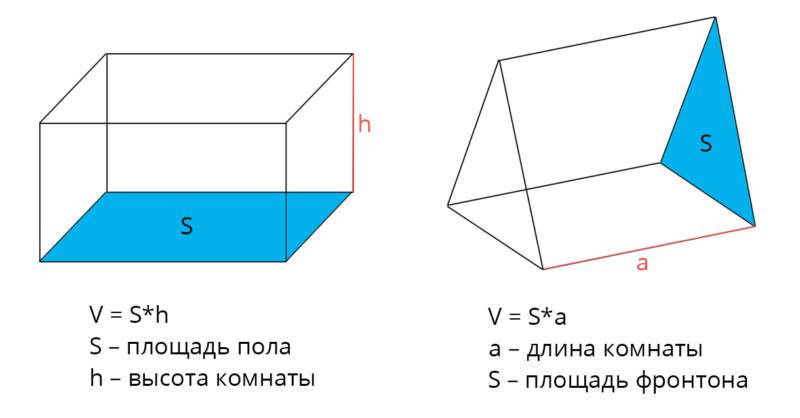
Считаем объем комнаты
При установке систем обогрева, вентиляции или кондиционирования нужно знать кубатуру помещения.

Стоит учесть, что после ремонта объем комнаты может уменьшиться на высоту стяжки и покрытия пола или на величину профиля натяжного потолка.
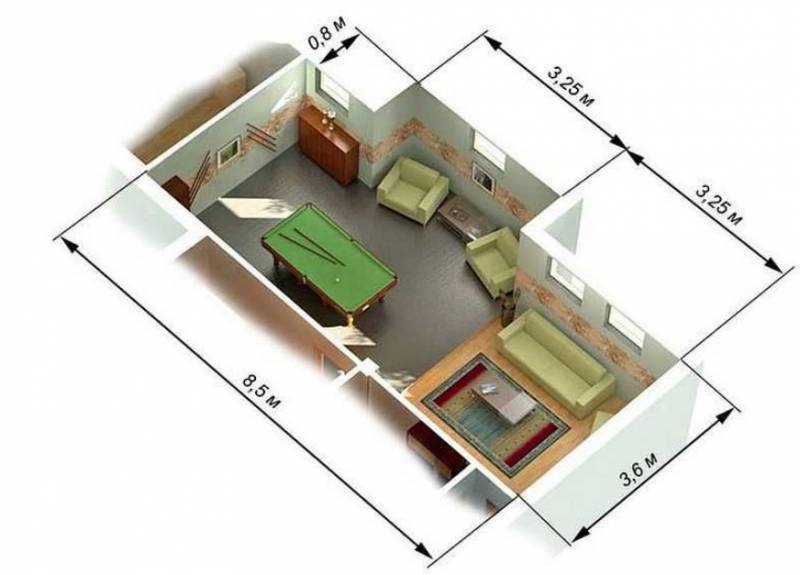
Для вычисления объема пространства правильной формы нужно перемножить три величины: ширину, длину и высоту комнаты:
- Например, объем помещения длиной 4 м и шириной 3 м с высотой потолков 2,7 м составляет: 4 × 3 × 2,7 = 32,4 м3.
- Если площадь комнаты известна, то расчеты упрощаются, даже для помещений сложной конфигурации алгоритм один и тот же — площадь умножается на высоту помещения.
- Если использовать предыдущий пример, то площадь комнаты составляет 12 м2, при высоте 2,7 м получаем: 12 × 2,7 = 32,4 м3.
При сложной конфигурации помещения расчеты имеют небольшую погрешность, при этом округлять цифры стоит в большую сторону и делать небольшой запас материалов.
Особенно если ремонт будет производиться своими силами без помощи профессионалов, и вероятны ситуации с переделкой брака или с большим количеством отходов.
Облегчить процесс расчетов можно используя онлайн калькуляторы для расчета площадей любой сложности, от элементарных до многоугольных.

Некоторые программы плюсом выдают чертеж комнаты в масштабе. Иногда стоит разобраться с мануалом программы, чтобы воспользоваться преимуществами калькуляторов:
- скорость;
- точность;
- возможность рассчитать поверхность любой геометрии.

Использование проверенных приемов и внимательность при измерениях позволит правильно сделать расчеты.

А также точно определить количество необходимых стройматериалов и распланировать ремонтные работы.
Фото расчетов площади комнаты



















Об авторе: Эксперт в области ремонта, внутренних отделок, кровли
Задать вопрос
Содержание материала
- Площадь застройки
- Видео
- Как высчитывается площадь помещения?
- Какую формулу можно применить для расчета размера жилой зоны в частном доме
- С чего начинать
- В каком классе изучают площадь прямоугольника?
Площадь застройки
Площадь застройки — площадь горизонтального сечения здания на уровне цоколя, включая его выступающие части. Крыльцо и пандус также включаются в площадь застройки, а выступающие части крыши — нет. Логика такая: на площади участка выделяются площадь застройки, отмостки, площадок, проездов, дорожек и т.д. Балкон на втором этаже, выступающий за пределы цоколя, не будет включен в площадь застройки, если только он не расположен на несущих столбах. Для владельца земельного участка существенным является «разрешенная площадь застройки», которая обычно не может превышать 30% общей площади участка.
Как высчитывается площадь помещения?
Автор вопроса: Создано:
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см). Как высчитать площадь комнаты. Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем.
Ответил(а): Климова Г. 09.03.22
Видео
Какую формулу можно применить для расчета размера жилой зоны в частном доме
С целью определения площади отведённой под жилую, нужно иметь размеры всех зон, предназначенных для жилья в данном доме.
Для того, чтобы выяснить, какие именно зоны в конкретном частном домовладении необходимо считать жилыми, достаточно развернуть и внимательно изучить проект дома и его технический паспорт. В экспликации к техпаспорту можно конкретно увидеть как величину площади, так и категорию каждой из комнат.
К комнатам, предназначенным для жилья можно отнести:
- Зал-гостиную.
- Комнаты -спальни.
- Гардеробную.
Для того, чтобы правильно замерить жилую площадь помещения, требуется тщательно замерить длину и ширину всех имеющихся стен в каждой из комнат, предусмотренных для постоянного в них нахождения. Это можно сделать при помощи строительной рулетки. Все измерения рекомендуется делать точно и аккуратно. Удобнее будет если перед снятием замеров вынести из комнат все ненужное, чтобы место у каждой из стен было в свободном доступе и после этого произвести измерения вдоль полового плинтуса. Все полученные результаты измерений с обязательной пометкой зоны, в которой они производились надо зафиксировать.
Когда измерения жилых помещений подойдут к концу и все точно записано, можно заняться подсчётом необходимой величины. Для её точного вычисления можно применить следующую формулу:
Д (длина) одной комнаты х Ш (ширина) одной комнаты =П (площадь) одной комнаты.
Результаты полученных измерений нужно записать, сделав пометки — такой шаг облегчит задачу в том случае, если вы в будущем соберётесь предпринять ещё какие-либо работы в доме. После этого, надо сложить все результаты замеров, полученные вами для каждой комнаты. Вычисленная величина и станет показателем жилой площади вашего домовладения.
С чего начинать
Самое время вспомнить школьную математику – чтобы рассчитать площадь, необходимы три параметра:
- Длина – обычно она бывает 4 либо 4,5 метра.
- Ширина – стандартное значение для большинства домов это 3 или 3,5 метра.
- Высота – в новостройках она обычно равна 2,5 метрам. А вот в постройках сталинской эпохи может составлять до 3 метров.
В решении задачи, как рассчитать площадь, не обойтись и без соответствующих инструментов:
- рулетки;
- строительного угольника;
- карандаша;
- калькулятора;
- строительного уровня.
Если планируются много писать, то вместо листка бумаги лучше взять блокнот либо тетрадь. Листики имеют свойство теряться, причём, когда нужно не всегда найдёшь их потом. Рулетка обязательно должна быть с фиксатором, иначе возникнуть сложности и процедура расчётов превратится в настоящее мучение.
В каком классе изучают площадь прямоугольника?
Автор вопроса: Создано:
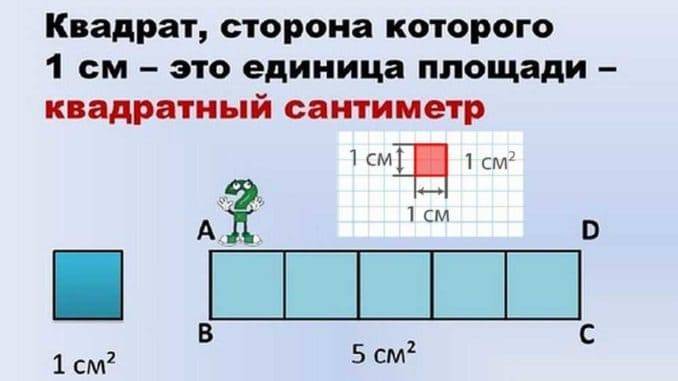
Математика 3 класс Урок№22 — Площадь прямоугольника. мы узнаем: способ вычисления площади прямоугольника; мы научимся: сравнивать геометрические фигуры по площади; мы сможем: вычислять площадь прямоугольника. Площадь – внутренняя часть геометрической фигуры. Площадь измеряется в квадратных сантиметрах. Чтобы найти площадь прямоугольника, надо его длину умножить на ширину. Интересные факты о геометрических фигурах Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров.
Ответил(а): Щукин Д. 22.03.22
