Как найти боковую поверхность наклонной треугольной призмы

Здесь вы найдёте: Объем правильной треугольной призмы понятие, Объем призмы треугольной формула нахождения, Площадь треугольной призмы

Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.

Призма треугольная — определение

Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

Элементы треугольной призмы

Треугольники ABC и A₁B₁C₁ являются основаниями призмы.

Четырехугольники A₁B₁BA, B₁BCC₁ и A₁C₁CA являются боковыми гранями призмы.

Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Виды треугольных призм

Треугольная призма бывает двух видов: прямая и наклонная.

У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)

Прямая треугольная призма

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.

Наклонная треугольная призма

Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.

Основные формулы для расчета треугольной призмы

Объем треугольной призмы

Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.

 Объем призмы = площадь основания х высота

или

V=S_осн ^. h

Площадь боковой поверхности призмы

Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.

Площадь боковой поверхности треугольной призмы = периметр основания х высота

или

S_бок=P_осн^.h 

Площадь полной поверхности призмы

Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.

так как S_бок=P_осн^.h, то получим:

S_{полн.пов.}=P_осн^.h+2S_осн

Правильная призма — прямая призма, основанием которой является правильный многоугольник.

Свойства призмы:

Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.

Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см², то высота должна быть выражена в сантиметрах, а объем — в см³ . Если площадь основания в мм², то высота должна быть выражена в мм, а объем в мм³ и т. д.

Пример призмы

В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2  · 6 · 8 · 5 = 120.

Задача 2.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение: 

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S₂ = S₁k² = S₁2² = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Таким образом, искомый объём равен 20.

При изучении стереометрии в старших классах школ рассматривают свойства фигур в пространстве. Одним из основных свойств является объем, однако иногда возникают геометрические проблемы, которые требуют вычисления площадей поверхностей фигур. В данной статье рассмотрим конкретный вопрос: по какой формуле площадь боковой поверхности треугольной призмы можно найти?

Треугольная призма

Для начала разберемся, какая фигура будет рассмотрена в статье. Призма – это такой геометрический объект, который состоит из двух одинаковых и параллельных многоугольных граней и нескольких произвольных параллелограммов, которые указанные грани соединяют между собой. Построить призму несложно. Для этого достаточно взять n-угольник плоский и параллельно самому себе перенести его в другую плоскость. В процессе переноса стороны n-угольника опишут все параллелограммы фигуры, совокупность которых образует боковую поверхность призмы. Сами же n-угольники называются ее основаниями.

Здесь мы не будем рассматривать все возможные виды призм, а сосредоточим свое внимание на треугольной фигуре. Несложно догадаться, что под ней понимают такую призму, n-угольные основания которой являются треугольниками. Причем треугольники могут быть самой разной формы, включая равнобедренные и равносторонние.

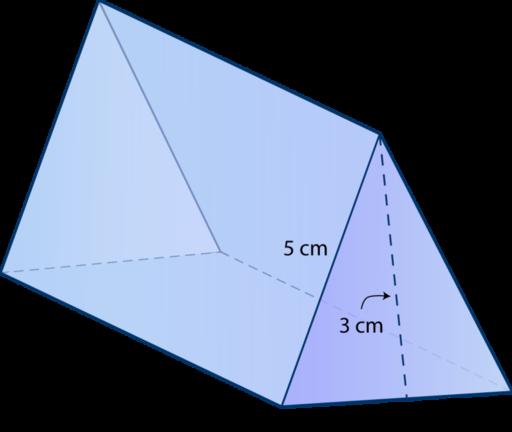
Таким образом, треугольная призма образована пятью гранями (2 треугольника и 3 параллелограмма). Фигура имеет 6 равноправных вершин и 9 ребер двух видов: ребра основания и ребра боковой поверхности. Выше показан пример такой призмы.

Виды призм треугольных

Рассматриваемая фигура является самой простой среди призм, поскольку треугольник – это основание с наименьшим возможным количеством сторон. Любая треугольная призма является выпуклой. В общем случае можно выделить три вида этой геометрической фигуры:

• наклонная;
• прямая;
• правильная.

Чтобы понимать разницу между указанными видами, следует обратить внимание на тип основания и боковых сторон. Так, если боковые стороны являются параллелограммами общей формы или ромбами, то призма однозначно будет наклонной. Если же боковые все грани образованы прямоугольниками или квадратами, то перед нами прямая призма. Последняя может быть также правильной, если все три прямоугольника являются одинаковыми. Другой критерий правильности прямой фигуры состоит в том, что у нее правильным является основание, то есть оно образовано треугольником с равными сторонами.

Далее рассмотрим формулы площади боковой поверхности треугольной призмы правильной, прямой, наклонной и отсеченной.

Наклонная призма

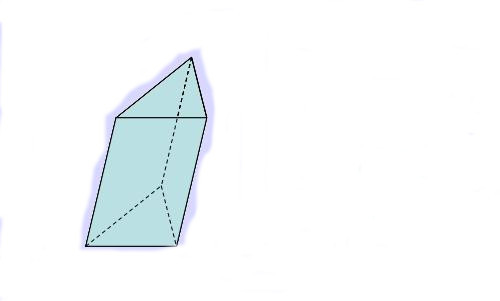
Речь идет о треугольной фигуре произвольного вида. Вычислить площадь боковой поверхности для нее сложнее всего, поскольку высота h фигуры (дистанция между основаниями) не совпадает с длиной бокового ребра b.

Если возникает задача определения площади поверхности (боковой) такой призмы, то поступают следующим образом: сначала делают воображаемый срез фигуры, который должен быть перпендикулярен всем боковым ребрам и граням. Затем рассчитывают периметр этого среза. В данном случае речь идет о периметре треугольника. Предположим, что он равен P_sr. Площадь боковой поверхности определяется путем умножения величины P_sr на сторону b, то есть имеет место следующая формула:

S_b = P_sr × b

Прямая призма

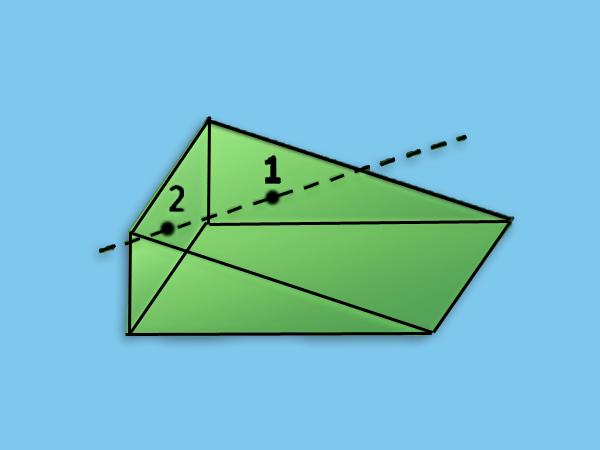
Как выше было сказано, поверхность боковая этой призмы образована тремя прямоугольниками. Две стороны этих прямоугольников являются одинаковыми, они равны длине бокового ребра b, которое также является высотой h фигуры. Что касается оставшихся двух сторон, то они могут отличаться. Эти стороны являются сторонами оснований. Обозначим их символом a_i, где i = 1, 2, 3. Тогда формула площади поверхности боковой прямой треугольной призмы запишется так:

S_b = b × ∑_i=1³a_i

Многие могли заметить, что данное выражение не отличается от аналогичного для призмы наклонной, ведь сумма трех сторон a_i является периметром основания. Это связано с тем, что для прямой фигуры основание является перпендикулярным боковым граням срезом.

Правильная фигура

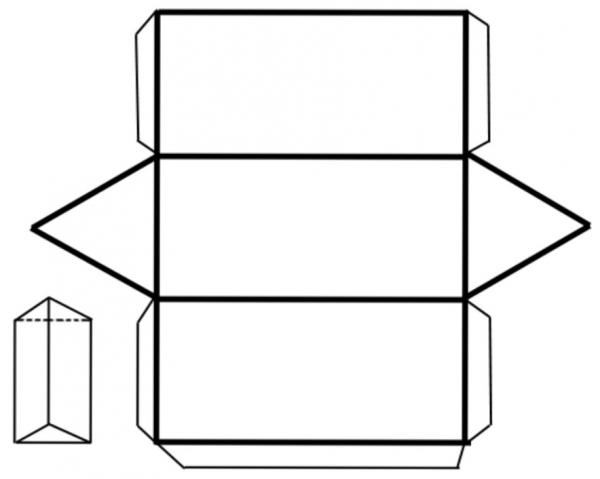
Формула площади поверхности боковой призмы треугольной правильной является самой простой по сравнению с выражениями выше. У правильной фигуры все боковые грани являются не просто прямоугольниками (квадратами в некоторых случаях), но еще они равны между собой. Эти геометрические факты позволяют записать формулу площади поверхности боковой призмы треугольной правильной в таком виде:

S_b = 3 × a × b

Здесь a – сторона основания (треугольника). Цифра 3 появляется потому, что боковая поверхность представлена тремя равными гранями. Напомним, что в данном выражении сторона b может быть заменена высотой h.

Очевидно, если боковые стороны представляют собой квадраты, то формула для S_b запишется так:

S_b = 3 × a²

Отсеченная фигура

Такая призма образуется, если с помощью плоскости отсечь ее часть. Если секущая плоскость параллельна основаниям, то формула площади боковой поверхности треугольной призмы отсеченной примет один из записанных в предыдущих пунктах вид. Действительно, при параллельном сечении мы получим аналогичную по форме исходной призме фигуру.

Если же секущая плоскость не будет параллельна основаниям, тогда для определения площади отсеченной призмы необходимо будет проводить специальный геометрический анализ, поскольку ее боковая поверхность будет представлена неправильными четырехугольниками.

• Задание 1
• Задание 2
• Задание 3

Другие уроки:

Многогранник, две грани которого равные -угольники, лежащие в параллельных плоскостях, а остальные  граней – параллелограммы, называют -угольной призмой. 

Два -угольника называют основаниями призмы, а параллелограммы – боковыми гранями. Стороны граней называют ребрами призмы, а концы ребер – вершинами призмы. 

На рисунке 9.41 изображена пятиугольная призма, на рисунке 9.42 – треугольная, а на рисунке 9.43 – четырехугольная. 

На рисунке 9.42 треугольники и – основания призмы , параллелограммы , , – боковые грани, отрезки , , – боковые ребра, отрезки ,  , , , , – ребра оснований, точки  ,  ,  ,  ,  ,  – вершины призмы.

Если грани призмы не имеют общего ребра, то их называют противоположными, если грани имеют общее ребро, то – смежными. На рисунке 9.43 грани  и ,  и , а также  и  являются противоположными, а, например, грани и  – смежными. 

Две вершины призмы, не принадлежащие одной грани, называют противоположными. Например, на рисунке 9.43 вершины  и  – противоположные. 

Диагональю призмы называют отрезок, соединяющий две противоположные вершины (например, диагональ  на рисунке 9.41). 

Треугольная призма не имеет противоположных граней, не имеет противоположных вершин и не имеет диагоналей.

Прямой призмой называют призму, боковые ребра которой перпендикулярны плоскостям ее оснований (рис. 9.42). Боковые грани прямой призмы – прямоугольники.

Наклонной призмой называют призму, боковые ребра которой являются наклонными к плоскостям ее оснований (рис. 9.41 и 9.43). Боковые грани наклонной призмы – параллелограммы (некоторые боковые грани могут быть и прямоугольниками).

Высотой призмы называют перпендикуляр, заключенный между основаниями призмы. Высота  прямой призмы равна длине ее бокового ребра (рис. 9.42), высота  наклонной призмы – не равна (рис. 9.41 и 9.43).

Диагональным сечением призмы называют сечение, содержащее диагональ призмы. На рисунке 9.44 построены диагональные сечения  и  четырехугольной призмы .

Параллелепипедом называют призму, основание которой – параллелограмм (рис. 9.44). 

Прямым параллелепипедом называют параллелепипед, боковые ребра которого перпендикулярны плоскостям его оснований (рис. 9.45). 

Прямоугольным параллелепипедом называют прямой параллелепипед, основанием которого является прямоугольник. На рисунке 9.46 изображен прямоугольный параллелепипед.

Свойство диагонали прямоугольного параллелепипеда: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений: 

 , (9.1)

где  ,  ,  – длины ребер, выходящих из одной вершины,  – диагональ параллелепипеда. 

Объем прямоугольного параллелепипеда находят по формуле: 

 . (9.2)

Кубом называют прямоугольный параллелепипед с равными ребрами. Все грани куба – квадраты (рис. 9.47).

Объем прямой призмы высоты  и периметром основания  находят по формуле: 

 . (9.6)

Площадь поверхности прямой призмы находят по формуле: 

 . (9.7)

Площадь боковой поверхности прямой призмы высоты  и периметром основания  находят по формуле:

 . (9.8)

Объем наклонной призмы можно вычислить по формуле:

 . (9.9) 

Площадь поверхности наклонной призмы можно вычислить по формуле:  

 , (9.10)

а также по формулам:

 , (9.9.1)

  , (9.10.1)

 где   сечение, перпендикулярное ребру   (рис. 9.48).

Правильной призмой называют прямую призму, основанием которой является правильный многоугольник. 

Пример 1. Найдите объем и площадь поверхности куба, зная, что его диагональ   см. 

Решение. Согласно формуле 9.5   и   см. По формуле 9.3  (), а по формуле 9.4  (). 

Ответ:    ;   . 

Пример 2. Найдите объем прямоугольного параллелепипеда, диагональ которого равна   , а его измерения относятся как  . 

Решение. Согласно условию задачи запишем измерения параллелепипеда:   ,   ,   .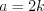

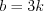Согласно свойству диагонали прямоугольного параллелепипеда 9.1, получим:  ,   , откуда   . Тогда   ,   ,   .

Зная три измерения параллелепипеда, по формуле 9.2 найдем его объем:   .

Ответ:   .

Пример 3. В основании прямой призмы лежит прямоугольный треугольник с катетами  см и  см. Высота призмы равна  см. Найдите площадь поверхности и объем призмы. 

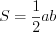Решение. 1. Площадь треугольника с катетами  и  найдем по формуле   . Получим:  ().

2. Гипотенузу  найдем по теореме Пифагора:  (см).

3. Площадь боковой поверхности призмы найдем по формуле 9.8 :   ().

4. Согласно формуле 9.7 , найдем площадь полной поверхности призмы: 

 ().

5. Объем призмы найдем по формуле 9.6 :

  ().

Ответ:   ;   . 

Пример 4. Объем наклонной треугольной призмы равен  , а боковое ребро   . Правильный треугольник   – сечение, перпендикулярное боковому ребру   (рис. 9.49). Найдите площадь боковой поверхности этой призмы. 

Решение. 1. Согласно формуле 9.9.1 запишем:   , откуда   .

2. Площадь правильного треугольника со стороной  находят по формуле   . Тогда   ,   ,   . 

3. Найдем периметр треугольника   :   . 

4. Согласно формуле 9.10.1 , найдем площадь боковой поверхности призмы:   . 

Ответ:   . 

Пример 5. Диагональ прямоугольного параллелепипеда равна  см, а диагонали его боковых граней равны  см и  см. Определите объем параллелепипеда.

Решение. Рассмотрим прямоугольный параллелепипед (рис. 9.50), где   ,   и   его измерения;  см – диагональ. 

Согласно свойству 9.1  . Рассмотрим треугольник  . Так как  см, то   . Рассмотрим треугольник . Так как  см, то   .

Запишем и решим систему уравнений  

Из второго уравнения системы выразим  и получим:   . Из третьего уравнения выразим  и получим:   . 

Подставим полученные значения   и   в первое уравнение системы и найдем значение :

 ,  ,  см.

Зная , определим значения   и  : 

 ,  см;  ,  см.

Согласно формуле 9.2  найдем объем параллелепипеда:  ().

Ответ:   . 

Пример 6. Определите объем правильной четырехугольной призмы, если ее диагональ образует с плоскостью боковой грани угол  , а сторона основания равна  .

Решение. Согласно условию задачи основанием призмы является квадрат со стороной  (рис. 9.51).

Так как отрезок   является проекцией диагонали призмы   на грань  , то угол   является углом наклона диагонали призмы к плоскости боковой грани и   .

Рассмотрим треугольник  . По свойству катета лежащего против угла  запишем  . 

Так как согласно свойству 9.1 диагонали прямоугольного параллелепипеда   , то   ,  ,   . 

Найдем объем призмы по формуле  9.9 :

 .

Ответ:   .

Пример 7. Найдите объем правильной шестиугольной призмы (рис. 9.52), зная, что большая диагональ призмы равна  и образует с плоскостью основания призмы угол   .

Решение. Рассмотрим большее диагональное сечение призмы  и прямоугольный треугольник 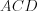. Поскольку диагональ призмы   и образует с плоскостью основания угол   , то катет , лежащий против угла   , равен половине гипотенузы, следовательно, высота призмы   .

Из теоремы Пифагора:  ,    ,   . 

Так как в основании призмы лежит правильный шестиугольник со стороной , то   и   . 

По формуле   найдем площадь основания призмы:   . 

По формуле 9.9 найдем объем призмы:   .

Ответ:   . 

1. Треугольная призма не имеет диагоналей.

2. Различайте прямую и наклонную призму: у наклонной призмы – боковые грани параллелограммы, у прямой призмы – боковые грани прямоугольники.

3. Если основание призмы – параллелограмм (ромб, прямоугольник, квадрат), то такую призму называют параллелепипедом. Длины ребер, выходящих из одной вершины параллелепипеда, называют его измерениями.

При изучении стереометрии в старших классах школ рассматривают свойства фигур в пространстве. Одним из основных свойств является объем, однако иногда возникают геометрические проблемы, которые требуют вычисления площадей поверхностей фигур. В данной статье рассмотрим конкретный вопрос: по какой формуле площадь боковой поверхности треугольной призмы можно найти?

Треугольная призма

Для начала разберемся, какая фигура будет рассмотрена в статье. Призма – это такой геометрический объект, который состоит из двух одинаковых и параллельных многоугольных граней и нескольких произвольных параллелограммов, которые указанные грани соединяют между собой. Построить призму несложно. Для этого достаточно взять n-угольник плоский и параллельно самому себе перенести его в другую плоскость. В процессе переноса стороны n-угольника опишут все параллелограммы фигуры, совокупность которых образует боковую поверхность призмы. Сами же n-угольники называются ее основаниями.

Вам будет интересно:Клонирование растений: этапы, примеры, плюсы и минусы

Здесь мы не будем рассматривать все возможные виды призм, а сосредоточим свое внимание на треугольной фигуре. Несложно догадаться, что под ней понимают такую призму, n-угольные основания которой являются треугольниками. Причем треугольники могут быть самой разной формы, включая равнобедренные и равносторонние.

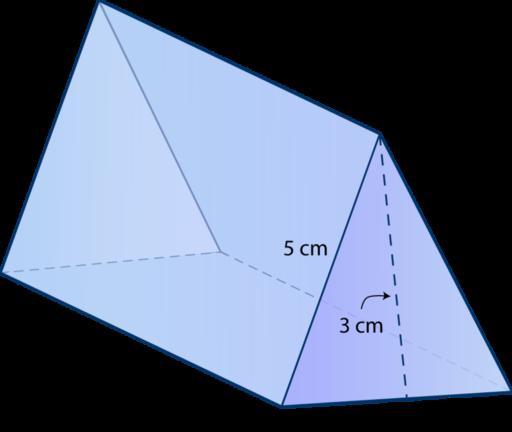
Таким образом, треугольная призма образована пятью гранями (2 треугольника и 3 параллелограмма). Фигура имеет 6 равноправных вершин и 9 ребер двух видов: ребра основания и ребра боковой поверхности. Выше показан пример такой призмы.

Виды призм треугольных

Рассматриваемая фигура является самой простой среди призм, поскольку треугольник – это основание с наименьшим возможным количеством сторон. Любая треугольная призма является выпуклой. В общем случае можно выделить три вида этой геометрической фигуры:

• наклонная;
• прямая;
• правильная.

Чтобы понимать разницу между указанными видами, следует обратить внимание на тип основания и боковых сторон. Так, если боковые стороны являются параллелограммами общей формы или ромбами, то призма однозначно будет наклонной. Если же боковые все грани образованы прямоугольниками или квадратами, то перед нами прямая призма. Последняя может быть также правильной, если все три прямоугольника являются одинаковыми. Другой критерий правильности прямой фигуры состоит в том, что у нее правильным является основание, то есть оно образовано треугольником с равными сторонами.

Далее рассмотрим формулы площади боковой поверхности треугольной призмы правильной, прямой, наклонной и отсеченной.

Наклонная призма

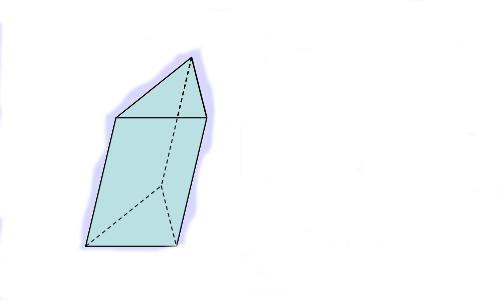
Речь идет о треугольной фигуре произвольного вида. Вычислить площадь боковой поверхности для нее сложнее всего, поскольку высота h фигуры (дистанция между основаниями) не совпадает с длиной бокового ребра b.

Если возникает задача определения площади поверхности (боковой) такой призмы, то поступают следующим образом: сначала делают воображаемый срез фигуры, который должен быть перпендикулярен всем боковым ребрам и граням. Затем рассчитывают периметр этого среза. В данном случае речь идет о периметре треугольника. Предположим, что он равен Psr. Площадь боковой поверхности определяется путем умножения величины Psr на сторону b, то есть имеет место следующая формула:

Sb = Psr × b

Прямая призма

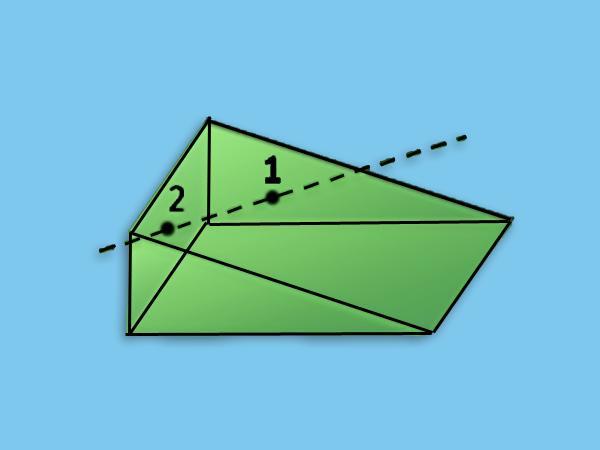
Как выше было сказано, поверхность боковая этой призмы образована тремя прямоугольниками. Две стороны этих прямоугольников являются одинаковыми, они равны длине бокового ребра b, которое также является высотой h фигуры. Что касается оставшихся двух сторон, то они могут отличаться. Эти стороны являются сторонами оснований. Обозначим их символом ai, где i = 1, 2, 3. Тогда формула площади поверхности боковой прямой треугольной призмы запишется так:

Sb = b × ∑i=13ai

Многие могли заметить, что данное выражение не отличается от аналогичного для призмы наклонной, ведь сумма трех сторон ai является периметром основания. Это связано с тем, что для прямой фигуры основание является перпендикулярным боковым граням срезом.

Правильная фигура

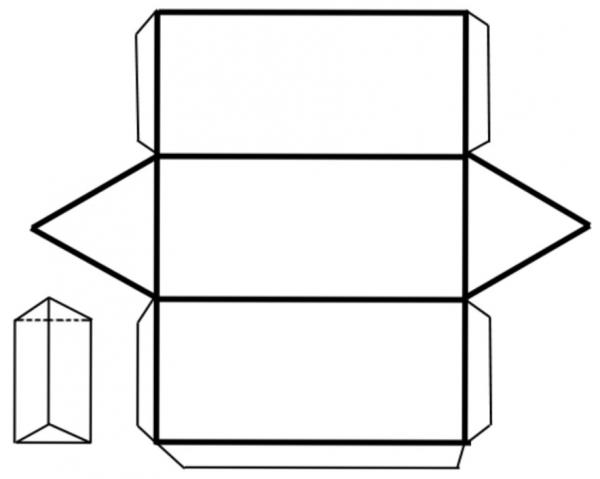
Формула площади поверхности боковой призмы треугольной правильной является самой простой по сравнению с выражениями выше. У правильной фигуры все боковые грани являются не просто прямоугольниками (квадратами в некоторых случаях), но еще они равны между собой. Эти геометрические факты позволяют записать формулу площади поверхности боковой призмы треугольной правильной в таком виде:

Sb = 3 × a × b

Здесь a – сторона основания (треугольника). Цифра 3 появляется потому, что боковая поверхность представлена тремя равными гранями. Напомним, что в данном выражении сторона b может быть заменена высотой h.

Очевидно, если боковые стороны представляют собой квадраты, то формула для Sb запишется так:

Sb = 3 × a2

Отсеченная фигура

Такая призма образуется, если с помощью плоскости отсечь ее часть. Если секущая плоскость параллельна основаниям, то формула площади боковой поверхности треугольной призмы отсеченной примет один из записанных в предыдущих пунктах вид. Действительно, при параллельном сечении мы получим аналогичную по форме исходной призме фигуру.

Если же секущая плоскость не будет параллельна основаниям, тогда для определения площади отсеченной призмы необходимо будет проводить специальный геометрический анализ, поскольку ее боковая поверхность будет представлена неправильными четырехугольниками.

Жду ваши вопросы и мнения в комментариях