Площадь боковой поверхности правильной пятиугольной призмы
Боковая поверхность правильной пятиугольной призмы складывается из пяти боковых граней:
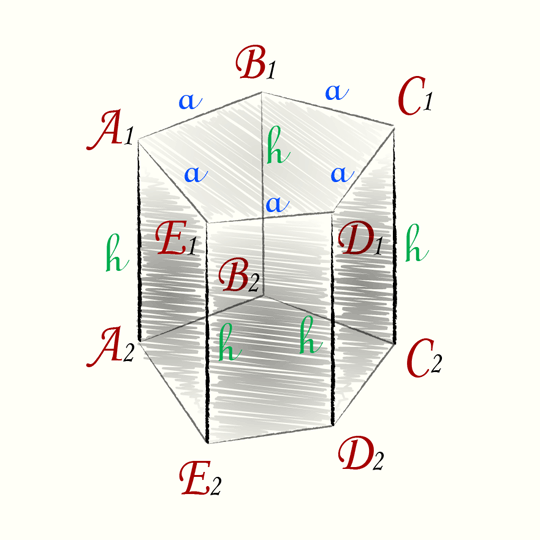
Площадь боковой поверхности правильной пятиугольной призмы
Пять боковых сторон представляют из себя прямоугольники со сторонами a и h
Таким образом площадь боковой поверхности правильной пятиугольной призмы есть сумма пяти площадей боковых граней.
[ S_{призмы} = 5S_{бок} ]
Подставим сюда формулу площади прямоугольника, получим:
[ S_{призмы} = 5ah ]
Вычислить, найти площадь боковой поверхности правильной пятиугольной призмы
площадь боковой поверхности правильной пятиугольной призмы |
стр. 338 |
|---|
In mathematics, a pentagonal prism is a three-dimensional geometric figure that has five lateral rectangular faces with two congruent and parallel pentagonal bases. A pentagonal prism is a type of heptahedron that belongs to the polyhedron family, which has seven plane faces. It has seven faces, ten vertices, and fifteen edges. The lateral, or side, faces of a pentagonal prism are rectangular-shaped and are connected by two identical pentagonal bases. There are three types of pentagonal prisms: regular pentagonal prism, right pentagonal prism, and oblique pentagonal prism. A pentagonal prism is called a regular pentagonal prism if it has sides that are of the same length. A right pentagonal prism is a prism that has congruent and parallel pentagonal faces perpendicular to the rectangular faces. An oblique pentagonal prism has pentagonal faces that are not exactly on top of each other, and the rectangular faces are not perpendicular to the pentagonal faces.

Pentagonal Prism
Surface Area of a Pentagonal Prism Formula
The surface area of a pentagonal prism is the total area occupied by all its surfaces. The surface area of the prism is equal to the area of its net. So, to determine the surface area of a pentagonal prism, we have to calculate the areas of each of its faces, and then add the resulting areas. A pentagonal prism has two types of surface areas: a lateral surface area and a total surface area.
So, the formula for calculating the lateral surface area (LSA) of a pentagonal prism is given as follows:
Lateral surface area of a pentagonal prism = 5as square units
where,
“a” is the apothem length of the pentagonal prism, and
“s” is the base length of the pentagonal prism.
The Total Surface Area of a Prism (TSA) = LSA + 2 × Base area
So, the formula for calculating the total surface area (TSA) of a pentagonal prism is given as follows:
Total surface area of a pentagonal prism = (5as + 5sh) square units
where,
“a” is the apothem length of the pentagonal prism
“s” is the base length of the pentagonal prism
“h” is the height of the prism.
Volume of a Pentagonal Prism Formula
The volume of a pentagonal prism is referred to as the space enclosed within a pentagonal prism. The formula for the volume of a pentagonal prism is equal to the product of its base area and its height.
Volume of a Pentagonal Prism (V) = Base Area × Height of the Prism
So, the formula for calculating the volume of a rectangular prism is given as follows:
Volume of a pentagonal Prism = (5/2) × a × s × h cubic units
where,
“a” is the apothem length of the pentagonal prism
“s” is the base length of the pentagonal prism
“h” is the height of the prism.
Solved Examples on Pentagonal Prism Formula
Example 1: Find the volume of a pentagonal prism whose apothem length is 5 cm, base length is 9 cm, and height is 12 cm.
Solution:
Given data:
Apothem length of the pentagonal prism (a) = 5 cm
The base length of the pentagonal prism (s) = 9 cm
Height of the pentagonal prism, h = 12 cm
We know that,
The volume of a pentagonal Prism = (5/2) × a × s × h cubic units
= 5/2 × (5 × 9 × 12)
= 5/2 × (540)
= 5 × 270 = 1,350
Therefore, the volume of the pentagonal prism is 1650 cm3.
Example 2: Find the height of the pentagonal prism if its volume is 1000 cu. in and its apothem length and base length are 4 in and 8 in, respectively.
Solution:
Given:
The volume of the pentagonal prism = 1000 cu. in
Apothem length of the pentagonal prism (a) = 4 in
The base length of the pentagonal prism (s) = 8 in
We know that,
The volume of a pentagonal Prism = (5/2) × a × s × h cubic units
⇒ 1000 = (5/2) × 4 × 8 × h
⇒ 1000 = 80h
⇒ h = 1000/80
⇒ h = 12.5 in
Therefore, the height of the pentagonal prism is 12.5 inches.
Example 3: Find the total surface area of the pentagonal prism whose apothem length is 6 in, base length is 10 in, and height is 13 in.
Solution:
Given data,
Apothem length of the pentagonal prism (a) = 6 in
The base length of the pentagonal prism (s) = 10 in
Height of the pentagonal prism, h = 13 in
We know that,
The total surface area of a pentagonal prism = 5as + 5sh square units
= 5 (6 × 10) + 5 (10 × 13)
= 5(60) + 5(150)
= 300 + 750
= 1050 sq. in
Therefore, the total surface area of a pentagonal prism is 1050 sq. inches.
Example 4: Find the lateral surface area of the pentagonal prism whose apothem length is 4 cm, base length is 7 cm, and height is 10 cm.
Solution:
Given data,
Apothem length of the pentagonal prism (a) = 6 in
The base length of the pentagonal prism (s) = 10 in
Height of the pentagonal prism, h = 13 in
We know that,
The lateral surface area of a pentagonal prism = 5as square units
= 5 × 4 × 10
= 200 sq. cm
Therefore, the lateral surface area of a pentagonal prism is 200 sq. cm.
Example 5: Find the volume of a pentagonal prism whose apothem length is 7 cm, base length is 11 cm, and height is 15 cm.
Solution:
Given data:
Apothem length of the pentagonal prism (a) = 7 cm
The base length of the pentagonal prism (s) = 11 cm
Height of the pentagonal prism, h = 15 cm
We know that,
The volume of a pentagonal Prism = (5/2) × a × s × h cubic units
= 5/2 × (7 × 11 × 15)
= 2,887.5 cm3
Therefore, the volume of the pentagonal prism is 2,887.5 cm3.
FAQs on Pentagonal Prism Formula
Question 1: What is a pentagonal prism?
Answer:
In mathematics, a pentagonal prism is a three-dimensional geometric figure that has five lateral rectangular faces with two congruent and parallel pentagonal bases. It has seven faces, ten vertices, and fifteen edges.
Question 2: What is the formula for calculating the total surface area of a pentagonal prism?
Answer:
The formula for calculating the total surface area (TSA) of a pentagonal prism is given as follows:
TSA = (5as + 5sh) square units
where,
“a” is the apothem length of the pentagonal prism
“s” is the base length of the pentagonal prism
“h” is the height of the prism.
Question 3: What is the formula for calculating the volume of a pentagonal prism?
Answer:
The volume of a pentagonal prism is referred to as the space enclosed within a pentagonal prism. The formula for calculating the volume of a rectangular prism is given as follows:
Volume of a pentagonal Prism = (5/2) × a × s × h cubic units
where,
“a” is the apothem length of the pentagonal prism
“s” is the base length of the pentagonal prism
“h” is the height of the prism.
Question 4: What is the formula for calculating the lateral surface area of a pentagonal prism?
Answer:
The formula for calculating the lateral surface area (LSA) of a pentagonal prism is given as follows:
LSA = 5as square units
where,
“a” is the apothem length of the pentagonal prism
“s” is the base length of the pentagonal prism
Question 5: What are the different types of a pentagonal prism?
Answer:
There are three types of pentagonal prisms: regular pentagonal prism, right pentagonal prism, and oblique pentagonal prism.
Related Resources
- Volume of Cone
- Surface Area of Sphere
- Volume of Cylinder
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
-
Формула площади правильной призмы
- 1. Общая формула
-
2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
- Примеры задач
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Sбок. = Pосн. ⋅ h
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы

Основание: равносторонний треугольник.
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 3ah |
| полная |  |
microexcel.ru
3. Площадь правильной четырехугольной призмы

Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 4ah |
| полная | Sполн. = 2a2 + 4ah |
microexcel.ru
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a2. А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a2.
4. Площадь правильной шестиугольной призмы

Основание: правильный шестиугольник
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 6ah |
| полная |  |
microexcel.ru
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:![]()
Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см2. Найдите ее высоту, если известно, что сторона основания равна 5 см.
Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:![]()
Боковая поверхность пятиугольной призмы
bgfn
Знаток
(266),
закрыт
11 лет назад
Помогите решить задачку по геометрии Т.Т
По ребру основания а и высоте b правильной пятиугольной призмы найдите ее боковую поверхность.
♑❇ɐʎlɐʇɐN❇♑
Высший разум
(827680)
11 лет назад
Боковые грани правильной призмы являются равными прямоугольниками.
Значит, площадь одной боковой грани S=ab
Сколько таких равных боковых граней в ПЯТИугольной призме? Пять
Значит, площадь всей боковой поверхности пятиугольной призмы равна площади одной боковой грани умноженной на 5.
S=5ab
Пятиугольная призма при решении задач по геометрии встречается гораздо реже, чем такие призмы, как треугольная, четырехугольная или шестиугольная. Тем не менее полезно рассмотреть основные свойства этой фигуры, а также узнать, как ее можно нарисовать.
Что собой представляет пятиугольная призма?
Речь идет об объемной фигуре, основания которой являются пятиугольниками, а боковые стороны – параллелограммами. Если каждый из этих параллелограммов будет перпендикулярен параллельным основаниям, то такая призма называется прямоугольной. Боковая поверхность прямоугольной пятиугольной призмы составлена из пяти прямоугольников. Причем прилегающая к основанию сторона каждого из них равна соответствующей длине стороны пятиугольника.
 Вам будет интересно:Формула для вычисления объема прямой призмы и примеры ее использования
Вам будет интересно:Формула для вычисления объема прямой призмы и примеры ее использования

Если пятиугольник будет правильным, то есть все его стороны и углы будут равны друг другу, тогда такая прямоугольная призма называется правильной. Далее в статье будем рассматривать свойства именно этой фигуры.
Элементы призмы
Для нее, как и для любой призмы, характерны следующие элементы:
- грани или стороны – это части плоскостей, ограничивающих фигуру в пространстве;
- вершины – точки пересечения трех сторон;
- ребра – отрезки пересечения двух сторон фигуры.
Числа всех названных элементов связаны друг с другом следующим равенством:
Число ребер = число вершин + число граней – 2
Это выражение носит название формулы Эйлера для полиэдра.
В пятиугольной призме количество сторон равно семи (два основания + пять прямоугольников). Число вершин составляет 10 (по пять для каждого основания). Число ребер в таком случае будет равно:
Число ребер = 10 + 7 – 2 = 15
Десять ребер принадлежат основаниям призмы, а пять ребер образованы прямоугольниками.
Как начертить пятиугольную призму?
Ответ на этот вопрос зависит от конкретной задачи. Если необходимо начертить произвольную призму, тогда следует изобразить любой пятиугольник. После этого провести пять параллельных отрезков равной длины из каждой вершины пятиугольника. Затем, соединить верхние концы отрезков. Получилась пятиугольная произвольная призма.
Если же следует начертить правильную призму, тогда вся сложность задачи сводится к получению правильного пятиугольника. Существует несколько способов начертить этот многоугольник. Здесь мы рассмотрим только два способа.

Первый способ заключается в построении окружности с помощью циркуля. Затем проводится произвольный диаметр окружности и от него отсчитывается с помощью транспортира пять углов по 72o (5*72o = 360o). При отсчете каждого угла делается насечка на окружности. Для построения прямоугольника остается соединить прямыми отрезками отмеченные насечки.
Второй способ предполагает использование только циркуля и линейки. Он является несколько сложным в сравнении с предыдущим. Ниже приводится видео, где подробно объясняется каждый шаг такого построения.

Заметим, что пятиугольник легко нарисовать, если соединить концы звезды. Если нет необходимости чертить точно правильный пятиугольник, тогда можно использовать способ со звездой, нарисованной от руки.
Как только пятиугольник изображен, следует из каждой его вершины провести пять одинаковых параллельных отрезков и соединить их вершины. Получится пятиугольная призма.
Площадь фигуры
Теперь рассмотрим вопрос, как найти площадь пятиугольной призмы. На рисунке ниже приведена ее развертка. Видно, что искомая площадь образована двумя одинаковыми пятиугольниками и пятью равными друг другу прямоугольниками.
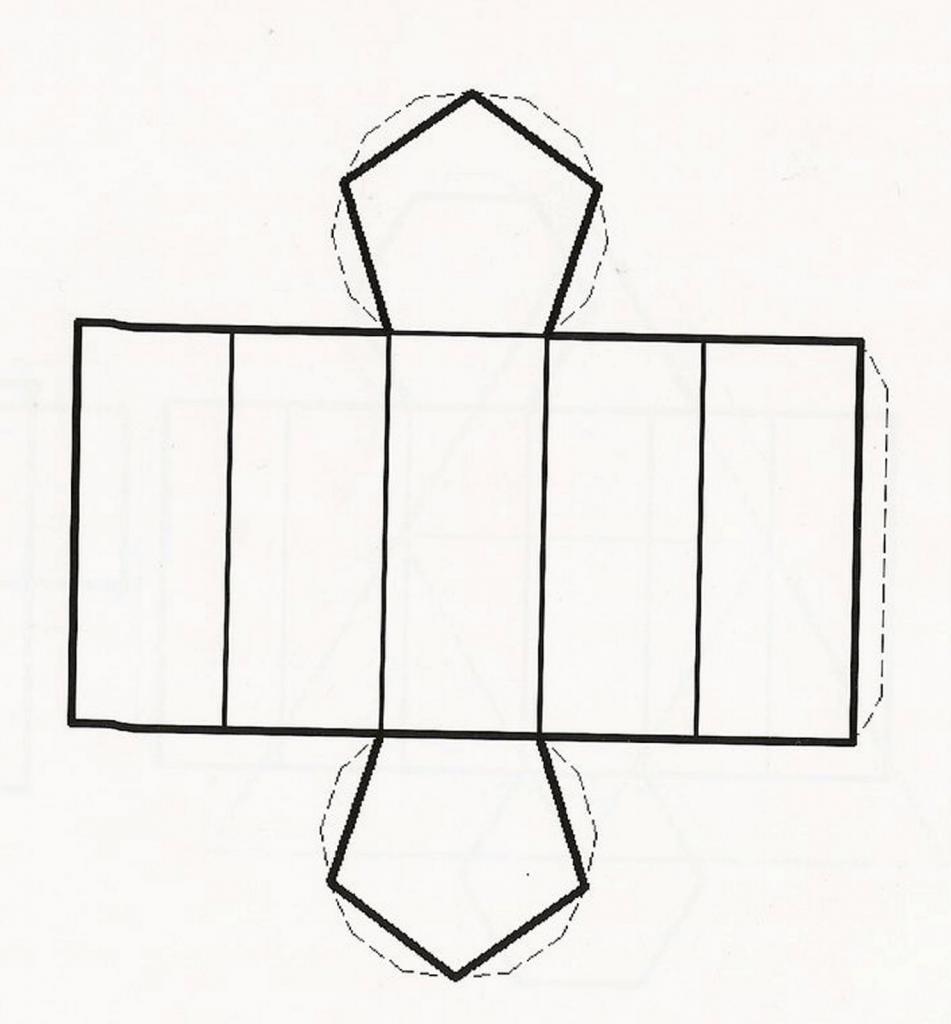
Площадь всей поверхности фигуры выразится формулой:
S = 2*So + 5*Sp
Здесь индексы o и p означают основание и прямоугольник соответственно. Обозначим длину стороны пятиугольника как a, а высоту фигуры как h. Тогда для прямоугольника запишем:
Sp = a*h
Чтобы вычислить площадь пятиугольника, воспользуемся универсальной формулой:
Sn = n/4*a2*ctg(pi/n)
Где n – число сторон многоугольника. Подставляя n = 5, получаем:
S5 = 5/4*a2*ctg(pi/5) ≈ 1,72*a2
Точность полученного равенства составляет 3 знака после запятой, что вполне достаточно для решения любых задач.
Теперь остается найти сумму полученных площадей основания и боковой поверхности. Имеем:
S = 2*1,72*a2 + 5*a*h = 3,44*a2 + 5*a*h
Следует помнить, что полученная формула справедлива только для прямоугольной призмы. В случае с косоугольной фигурой площадь ее боковой поверхности находят, исходя из знания периметра среза, который должен быть перпендикулярен всем параллелограммам.
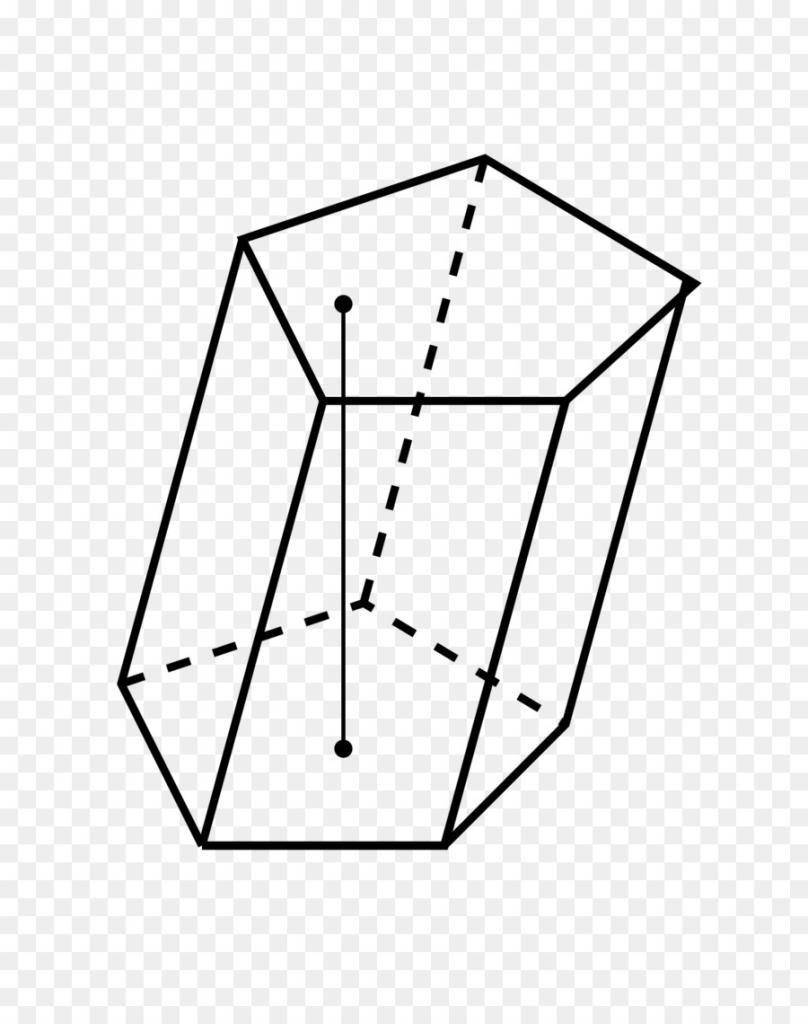
Объем фигуры
Формула расчета объема пятиугольной призмы ничем не отличается от аналогичного выражения для любой другой призмы или цилиндра. Объем фигуры равен произведению ее высоты на площадь основания:
V = So*h
Если рассматриваемая призма является прямоугольной, тогда высота в ней является длиной ребра, образованного прямоугольниками. Площадь правильного пятиугольника была вычислена выше с высокой точностью. Подставим это значение в формулу для объема и получим необходимое выражение для пятиугольной правильной призмы:
V = 1,72*a2*h
Таким образом, вычисление объема и площади поверхности пятиугольной правильной призмы возможно, если известна сторона основания и высота фигуры.
