Как найти боковую сторону имея 2 основания

Amaxar 777

Высший разум

(104705)


4 года назад

Меньшее основание: c1 = a
Большее основание: c2 = a + 2b
Тогда разность оснований: c2 – c1 = (a+2b)-a = 2b
Тогда: b = (c2-c1)/2
b – катет прямоугольного треугольника, прилежащий к острому углу, боковая сторона X – гипотенуза.
cos(ф) = b/X
X = b/cos(ф)
Т. к. sin(ф) ^2 + cos(ф) ^2 = 1:
cos(ф) = sqrt(1 – sin(ф) ^2) = sqrt(1 – 9/25) = 4/5
Тогда X = 5 b / 4
Или X = 5 (c2 – c1) / 8

Как посчитать стороны равнобедренного треугольника

Онлайн калькулятор

Чтобы вычислить длины сторон равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):

• длину основания (b) и угол α
• длину основания (b) и угол β
• длину основания (b) и высоту (h)

• длину двух равных сторон (a) и угол α
• длину двух равных сторон (a) и угол β
• длину двух равных сторон (a) и высоту (h)

Введите их в соответствующие поля и получите результат.

Как посчитать сторону a равнобедренного треугольника

Если известна сторона b и угол α

Чему равна сторона a равнобедренного треугольника если длина основания , а угол

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол α?

Формула

Пример

Если сторона b = 10 см, а ∠α = 30°, то:

Если известна сторона b и угол β

Чему равна сторона a равнобедренного треугольника если длина основания , а угол

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол β?

Формула

Пример

Если сторона b = 10 см, а ∠β = 30°, то:

a = 10 /_{2⋅sin 15} = 10/(2⋅0.2588) = 19.31см

Если известна сторона b и высота h

Чему равна сторона a равнобедренного треугольника если длина основания , а высота

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и высота h?

Формула

Пример

Если сторона b = 10 см, а высота h = 20 см, то:

a = √ 1 /_{10 2} + 20 2 = √ 0.01+400 = 20.61см

Как посчитать сторону b (основание) равнобедренного треугольника

Если известна сторона a и угол α

Чему равна сторона b равнобедренного треугольника если длина стороны , а угол

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол α?

Формула

Пример

Если сторона a = 10 см, а ∠α = 30°, то:

b = 2⋅10⋅cos 30° = 2⋅10⋅0.8660 = 17.32см

Если известна сторона a и угол β

Чему равна сторона b равнобедренного треугольника если длина стороны , а угол

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол β?

Формула

Пример

Если сторона a = 10 см, а ∠β = 40°, то:

Если известна сторона a и высота h

Чему равна сторона b равнобедренного треугольника если длина стороны , а высота

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и высота h?

Формула

b = 2⋅ √ a 2 – h 2 , h

Пример

Если сторона a = 10 см, а высота h = 5 см, то:

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника

α , β , γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b – катеты

c – гипотенуза

α , β – острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β , γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Стороны равнобедренного треугольника

Свойства

Равнобедренный треугольник имеет две равные по значению боковые стороны a и основание b. Это позволяет рассчитать любые параметры треугольника, необходимые для решения задачи. Периметр равнобедренного треугольника равен удвоенной боковой стороне в сумме с основанием. (рис.88.1) P=2a+b

Высота, проведенная к основанию равнобедренного треугольника, делит его на два конгруэнтных прямоугольных треугольника, с половиной основания в качестве второго катета и боковой стороной как гипотенузой. Такая высота одновременно является и медианой и биссектрисой. Найти ее можно по теореме Пифагора из прямоугольного треугольника. (рис.88.2) h_b=m_b=l_b=√(a^2-(b/2)^2 )=√(4a^2-b^2 )/2

Остальные две высоты равны друг другу и считаются через формулу с произведением разностей полупериметров и сторон, где приравнены боковые стороны. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a

Зная высоту, найти площадь равнобедренного треугольника можно, подставив полученное выражение в формулу, по которой площадь равна половине основания, умноженной на его высоту. S=hb/2=(b√(4a^2-b^2 ))/4

Углы в равнобедренном треугольнике распределяются следующим образом – углы при основании друг другу конгруэнтны, также как и боковые стороны, а в сумме все три угла дают 180 градусов, поэтому найти их можно двумя видами разности. α=(180°-β)/2 β=180°-2α

Если ни один из углов не дан, но есть все стороны, то можно воспользоваться теоремой косинусов, чтобы найти любой угол. cos⁡α=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cos⁡β=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 )

Медиана и биссектриса, опущенные на основание, вычисляются по формуле высоты, приведенной выше, а оставшиеся две медианы (равно как и две биссектрисы) равны друг другу, поскольку строятся на равных боковых сторонах. Вычислить медиану можно, упростив формулу произвольного треугольника. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2

В формуле биссектрисы аналогично приравниваются боковые стороны, и ее становится возможным вычислить по упрощенной схеме. (рис. 88.4) l_a=√(ab(2a+b)(a+b-a) )/(a+b)=(b√(a(2a+b) ))/(a+b)

Средняя линия равнобедренного треугольника, параллельная основанию, равна его половине, а средние линии, параллельные боковым сторонам, равны между собой и также равны половинам самих боковых сторон. (рис. 88.5) M_b=b/2 M_a=a/2

Радиус окружности, вписанной в равнобедренной треугольник, является производной формулы для произвольного треугольника, и рассчитать его можно, зная боковую сторону и основание. (рис. 88.6) r=b/2 √((2a-b)/(2a+b))

Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы и выглядит упрощенно следующим образом. (рис. 88.7) R=a^2/√(4a^2-b^2 )

[spoiler title=”источники:”]

http://www-formula.ru/2011-10-09-11-08-41

http://geleot.ru/education/math/geometry/calc/triangle/isosceles_triangle_sides

[/spoiler]

Трапеция — это выпуклый четырехугольник с двумя параллельными основами и двумя непараллельными
боковыми сторонами.

Иногда фигура определяется как четырёхугольник, у которого пара противолежащих сторон параллельна,
поэтому параллелограмм и прямоугольник являются частными случаями трапеции. Также это
четырехугольник, у которого одна пара противоположных сторон параллельна, а остальные стороны не
равны между собой.
Параллельные стороны называются основами, а остальные боковыми.

Вычисление стороны необходимо для нахождения периметра, площади трапеции, ее диагоналей и других
значимых параметров.

Длина основания через среднюю линию и известное основание

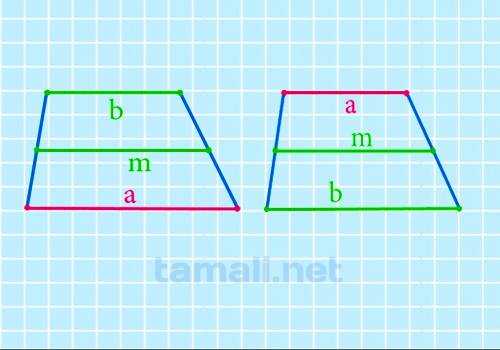
Средняя линия — отрезок, соединяющий середины боковых сторон фигуры. Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:

a = 2m – b

Например, средняя линия MN равна 6, а основание а – 9. Соответственно, значения, подставленные в
формулу, показывают, что b = 2*6 – 9 = 3.

Нижнее основание через верхнее основание, высоту и углы при нижнем основании

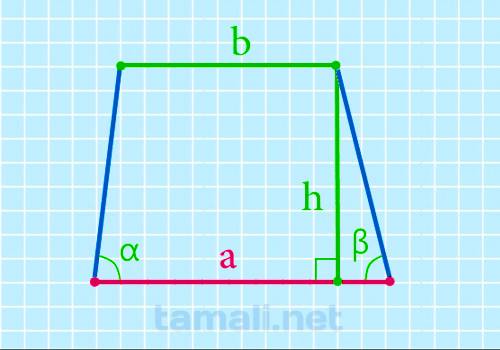
Высота h или BK – перпендикуляр, проведенный от одной основы к другой. Высота проводится в любой их
точке, но удобнее всего это делать из вершины углов при меньшей основе. Чтобы найти нижнее
основание, надо к верхнему прибавить произведение высоты на сумму котангенсов углов при нижнем:

a = b + h*(ctga + ctgb)

Дано верхнее основание 10, высота 6 и углы 30 и 45. По формуле а = 10 + 6*(3+1) = 10 + 63 + 6 = 16+63.
Для равнобедренного четырёхугольника выведены две формулы. В первой (a = 2S/h – b) основа выражена с
помощью формулы площади. Пример: Площадь равнобедренной трапеции ABCD = 18, высота = 6, а AD = 5.
Найти BC. BC = 2*18/6 – 5 = 6 – 5 = 1

Второе выражение сформулировано следующим образом: (a = b + 2h*ctga). Высота АН в трапеции ADEF =
10, DE = 4, а DAF = 45 градусам. Найти AF: AF = 4 + 10*2*1 = 24

Верхнее основание через нижнее основание, высоту и углы при нижнем основании

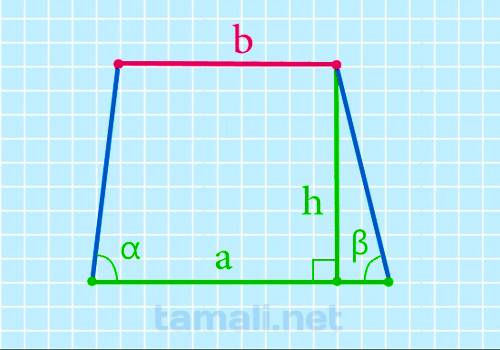
Чтобы найти верхнюю основу, надо из нижней вычесть произведение высоты на сумму котангенсов углов при
ней:

b = a – h*(ctg α + ctg β)

Дана трапеция с нижним основанием 15, высотой 8 и углами в 45 градусов. По формуле а = 15 + 8*(1+1) =
15 + 16 = 31

Формулы для равнобедренного четырёхугольника: b = 2S/h – a и b = a – 2h*ctga.

• Площадь трапеции KLMN = 44, KL=MN, высота равна 8, KN = 5. Найти LM: LM = 44*2/8 – 5 = 6
• Высота трапеции DEFG = 15, DG= 5, а EDG = 45 градусам. Найти EF: EF = 5 + 15*2*1 = 35

Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании

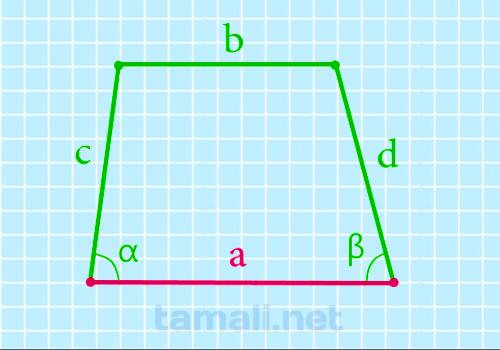
Для нахождения основы а нужно к основе b прибавить произведение одной и другой стороны и косинусов
углов при них

a = b + c * cos α + d * cos β

Дана равнобокая трапеция с верхним основанием 6, боковыми сторонами 5 и 11 и углами в 45 градусов.
Найти нижнее основание: а = 6 + 5*2/2 + 11*2/2 = 6 + 162/2 = 6 + 82

Отдельно для подобного типа фигур было выведено два выражения: a = (d1^2 – c^2)/b и a = b +
2c*cosa.

• трапеции ABCD AB = CD = 8, диагональ AC = 12, а BC = 4. Вычислить AD: AD = (12*12 – 8*8)/4
  = (144 – 64)/4 = 20
• В трапеции KLMN KL = MN = 4, LM = 7, а LKN равен 30 градусам. Вычислить KN: KN = 7 +
  4*2*3/2 = 7 + 43

Верхнее основание через боковые стороны, нижнее основание и углы при нем

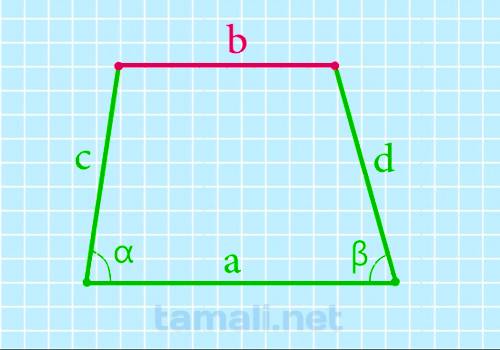
Для нахождения основы b нужно из основы а вычесть произведение одной и другой боковой стороны и углов
при них

b = a – c * cos α – d * cos β

Дана трапеция с нижним основанием 27, боковыми сторонами 20 и 14 и углами в 30 и 60 градусов. Найти
верхнее основание: b = 27 — 20*3/2 — 14*1/2 = 27 — 103 — 7 = 20 —
103. Формулы для равнобедренного типа: b = (d1^2 — c^2)/a и b = a — 2c*cosa.

• В трапеции DEFG DE и FG = 11, диагональ АС = 13, а EF = 12. Вычислить DG: DG = (13*13 –
  11*11)/12= (169 – 121)/12 = 4
• Боковые стороны трапеции BCDE BC и DE = 25, BE = 10, а CBE равен 60 градусам. Вычислить CD:
  CD = 25 – 10*2*1/2 = 15

Боковая сторона через высоту и угол при нижнем основании

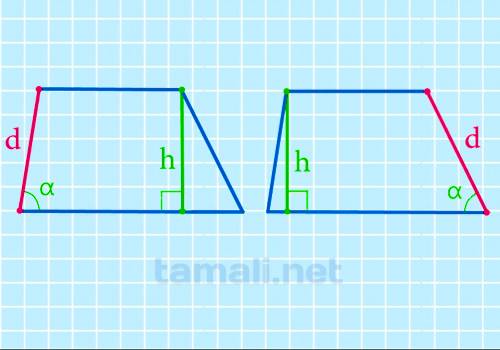
Чтобы найти боковую сторону, надо разделить высоту на синус угла при ней

d = h / sin α

Дана трапеция с высотой 12 и углами в 30 и 60 градусов. Найти боковые стороны: c = 12/0,5 =
24, d = 12/3/2 = 243

Для прямоугольного типа формулы несколько отличаются. Самая простая из них связывает высоту и меньшую
боковую сторону: c = h.
Для нее существует еще несколько формул: с = d*sina; c = (a – b)*tga; c
= (d^2 – (a – b)^2)

• В прямоугольной трапеции CDEF сторона EF равна 22, а прилежащий угол = 45. Найти CD. CD =
  22*2/2 = 112
• Прямоугольная трапеция MNOP имеет основания MP и NO, равные 32 и 19 соответственно. NMP равен 60
  градусам. Найти MP: MP = (32 – 19)*3 = 133
• В прямоугольной трапеции ABCD AD и BC равны 35 и 15 соответственно. Диагональ АС = 26. Найти AB.
  AB = (26^2 – (35 – 15)^2) = 676 – 400 = 276 = 269

Первая вытекает из прямоугольного треугольника и свидетельствует о том, что отношение катета к
гипотенузе равно синусу противолежащего угла. В этом треугольнике второй катет равен разности двух
оснований. Отсюда возникает утверждение, приравнивающее тангенс угла к отношению катетов. Третья
формула выведена на основании теоремы Пифагора.

Для второй боковой стороны выведено и записано три выражения: d = (a — b)/cosa; d = c/sina; d =
(c^2 — (a — b)^2). Первое и второе получаются из соотношения сторон в прямоугольном
треугольнике, а третье выводится из теоремы Пифагора.

• В прямоугольной трапеции KLMN KN = 28, LM = 13 а прилежащий угол = 30. Найти KL: KL = (28 –
  13)/3/2 = 103
• В прямоугольной трапеции EFGH EF равна 45. FEH равен 30 градусам. Найти GH: GH = 45/0,5 =
  90
• В прямоугольной трапеции NOPQ NQ и OP =.36 и 17. Диагональ равна 29. Найти NO: NO = (29^2 –
  (36 – 17)^2) = 841 – 361= 480 = 430

Для равнобокой трапеции существуют формулы c = d1^2 – ab; c = (a – b)/2cosa; c = S/m*sina; c =
2S/(a+b)*sina.

• В трапеции LMNO LM = NO. LO = 16, MN = 6, диагональ равна 10. Найти LM: LM = 10^2 – 16*6 =
  100 – 96 = 4
• Трапеция ABCD – равнобокая, AB = CD. AD = 18, BC = 4, а прилежащий угол равен 45 градусам. Найти
  AB: AB = (18 – 4)/2/2 = 14/2/2 = 14/2
• В трапеции BCDE BC=DE. Площадь фигуры равна 48, BE = 17, CD = 7, а CBE равен 30 градусам.
  Вычислить BC: m = (17 – 7)/2 = 5, BC = 48/5*1/2 = 96/5 = 19,2
• Площадь равнобедренной трапеции KLMN = 90, основания KN и LM = 32 и 18 соответственно, а LKN =
  60 градусов. Вычислить KL: KL = 2*90/(32 + 18)*3/2 = 360/503 = 129600/7500 = 17,28

Виды трапеций

Существуют следующие виды трапеций:

• Равнобедренная трапеция — фигура, у которой боковые стороны и углы при основании равны.
  Диагонали также равны. Треугольники, образованные диагоналями и основой, являются
  равнобедренными. Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
  разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
  фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб.
• Прямоугольная трапеция — фигура, у которой одна из боковых сторон перпендикулярна основам
  и равна высоте. Два угла будут равны 90 градусам, и они всегда принадлежат смежным вершинам, а
  другие всегда острый и тупой, их сумма всегда будет равна 180 градусам. Каждая диагональ
  образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из
  вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, другая прямоугольный
  треугольник.
• Разносторонняя трапеция — фигура, боковые стороны которой не равны и углы при основании не
  являются прямыми. Ее диагонали делят фигуру на четыре треугольника, два из которых подобны, а
  остальные — равновелики, то есть имеют одинаковые площади. Сумма углов при боковой стороне 180
  градусов.

Свойства трапеции

1. Средняя линия параллельна основаниям и равна их полусумме.
2. Любая биссектриса, выведенная из угла четырёхугольника, отсекает на основании (продолжении)
   отрезок с длиной боковой стороны.
3. Треугольники AOD и COD, образованные отрезками диагоналей и основами, подобны.
   Коэффициент
   подобия – k = AD/BC.
   Отношение площадей треугольников — k^2.
4. Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами, имеют одинаковую
   площадь.
5. В трапецию можно вписать окружность, если сумма оснований равняется сумме её боковых сторон.
6. Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений
   боковых сторон лежат на одной прямой.
7. Отрезок, соединяющий середины диагоналей, равняется половине разности основ и лежит на средней
   линии.

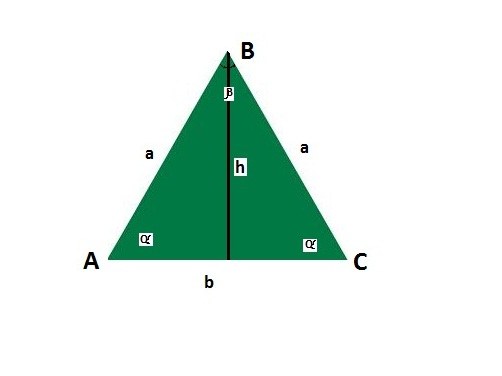
Как найти боковую сторону равнобедренного треугольника, если дано основание

Треугольник, который имеет две равные по длине стороны, называют равнобедренным. Эти стороны считаются боковыми, а третью именуют основанием. Одно из важных свойств равнобедренного треугольника: углы, противолежащие его равным сторонам, равны между собой.

Вам понадобится

• – таблицы Брадиса;
• – калькулятор;
• – линейка.

Инструкция

Обозначьте стороны и углы равнобедренного треугольника. Пусть основание будет b, боковая сторона a, углы между боковой стороной и основанием α, угол, противолежащий основанию β, высота h.

Найдите боковую сторону с помощью теоремы Пифагора, которая гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов – с^2=а^2+b^2. Если у равнобедренного треугольника помимо основания известна высота, то по свойствам равнобедренного треугольника она является его медианой и делит геометрическую фигуру на два равных прямоугольных треугольника.

Подставьте в уравнение нужные значения. Итак, в данном случае получится: а^2 = (b/2)^2+h^2. Решите уравнение: а = √(b/2)^2+h^2. Другими словами, боковая сторона равна квадратному корню, извлеченному из суммы половины основания, возведенного в квадрат, и высоты, которая также взята в квадрате.

Если равнобедренный треугольник – прямоугольный, углы при его основании равны 45°. Посчитайте размер боковой стороны с помощью теоремы синусов: a/sin 45°= b/sin 90°, где b – основание, а – боковая сторона, sin 90° равен единице. В итоге получается: a = b*sin 45°= b*√2/2. То есть, боковая сторона равна основанию, умноженному на корень из двух, деленный на два.

Используйте теорему синусов и в том случае, когда равнобедренный треугольник не прямоугольный. По основанию и прилежащему к нему углу α найдите боковую сторону: a = b*sinα/sinβ. Угол β вычислите с помощью свойства треугольников, которое гласит, что сумма всех углов треугольника равна 180°: β = 180°- 2*α.

Примените теорему косинусов, в соответствии с которой квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения данных сторон, умноженного на косинус угла между ними. По отношению к равнобедренному треугольнику приведенная формула выглядит таким образом: a = b/2cosα.

Источники:

• Найдите боковую сторону

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

1. Найти все стороны треугольника.
2. Найти все углы треугольника.
3. Найти площадь (S) и периметр (P) треугольника.
4. Найти радиус (r) вписанной окружности.
5. Найти радиус (R) описанной окружности.
6. Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
 

Сторона треугольника (или длина сторон) может быть найдена различными методами. 
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b – катеты, с – гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b – катеты, с – гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.

​​​​​Для равностороннего треугольника:

1) Найти сторону через площадь

где a – искомая сторона, S – площадь треугольника.

2) Найти сторону через высоту

где a – искомая сторона,h – высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a – искомая сторона,r – радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a – искомая сторона,R – радиус описанной окружности.

​​​​​Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a – искомая сторона, b – известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word