Трапеция — это выпуклый четырехугольник с двумя параллельными основами и двумя непараллельными
боковыми сторонами.
Иногда фигура определяется как четырёхугольник, у которого пара противолежащих сторон параллельна,
поэтому параллелограмм и прямоугольник являются частными случаями трапеции. Также это
четырехугольник, у которого одна пара противоположных сторон параллельна, а остальные стороны не
равны между собой.
Параллельные стороны называются основами, а остальные боковыми.
Вычисление стороны необходимо для нахождения периметра, площади трапеции, ее диагоналей и других
значимых параметров.
- Длина основания через среднию линию и другое известное
основание - Нижнее основание через верхнее основание, высоту и углы при
нижнем основании - Верхнее основание через нижнее основание, высоту и углы при
нижнем основании - Нижнее основание через боковые стороны, верхнее основание и
углы при нижнем основании - Верхнее основание через боковые стороны, нижнее основание и
углы при нижнем основании - Боковую сторону через высоту и угол при нижнем
основании
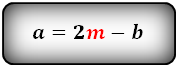
Длина основания через среднюю линию и известное основание
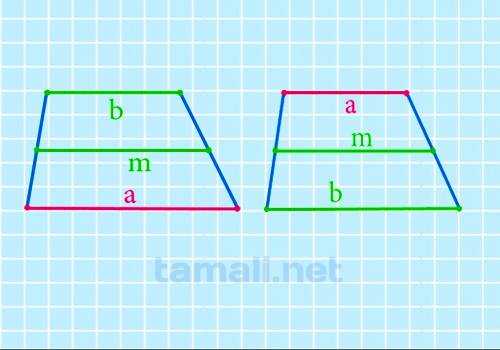
Средняя линия — отрезок, соединяющий середины боковых сторон фигуры. Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:
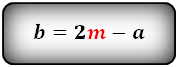
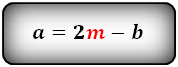
a = 2m – b
Цифр после
запятой:
Результат в:
Например, средняя линия MN равна 6, а основание а – 9. Соответственно, значения, подставленные в
формулу, показывают, что b = 2*6 – 9 = 3.
Нижнее основание через верхнее основание, высоту и углы при нижнем основании
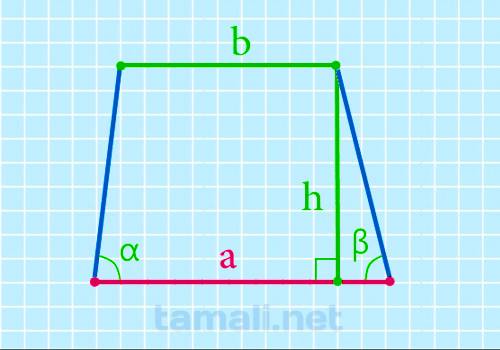
Высота h или BK – перпендикуляр, проведенный от одной основы к другой. Высота проводится в любой их
точке, но удобнее всего это делать из вершины углов при меньшей основе. Чтобы найти нижнее
основание, надо к верхнему прибавить произведение высоты на сумму котангенсов углов при нижнем:
a = b + h*(ctga + ctgb)
Цифр после
запятой:
Результат в:
Дано верхнее основание 10, высота 6 и углы 30 и 45. По формуле а = 10 + 6*(3+1) = 10 + 63 + 6 = 16+63.
Для равнобедренного четырёхугольника выведены две формулы. В первой (a = 2S/h – b) основа выражена с
помощью формулы площади. Пример: Площадь равнобедренной трапеции ABCD = 18, высота = 6, а AD = 5.
Найти BC. BC = 2*18/6 – 5 = 6 – 5 = 1
Второе выражение сформулировано следующим образом: (a = b + 2h*ctga). Высота АН в трапеции ADEF =
10, DE = 4, а DAF = 45 градусам. Найти AF: AF = 4 + 10*2*1 = 24
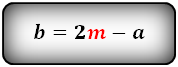
Верхнее основание через нижнее основание, высоту и углы при нижнем основании
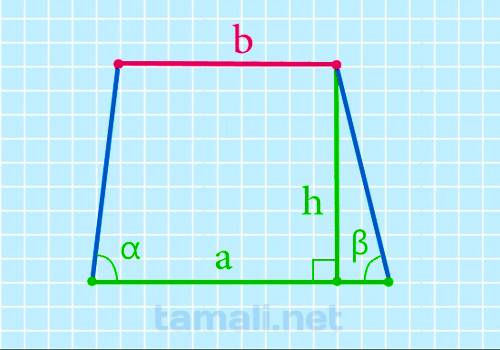
Чтобы найти верхнюю основу, надо из нижней вычесть произведение высоты на сумму котангенсов углов при
ней:
b = a – h*(ctg α + ctg β)
Цифр после
запятой:
Результат в:
Дана трапеция с нижним основанием 15, высотой 8 и углами в 45 градусов. По формуле а = 15 + 8*(1+1) =
15 + 16 = 31
Формулы для равнобедренного четырёхугольника: b = 2S/h – a и b = a – 2h*ctga.
- Площадь трапеции KLMN = 44, KL=MN, высота равна 8, KN = 5. Найти LM: LM = 44*2/8 – 5 = 6
- Высота трапеции DEFG = 15, DG= 5, а EDG = 45 градусам. Найти EF: EF = 5 + 15*2*1 = 35
Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании
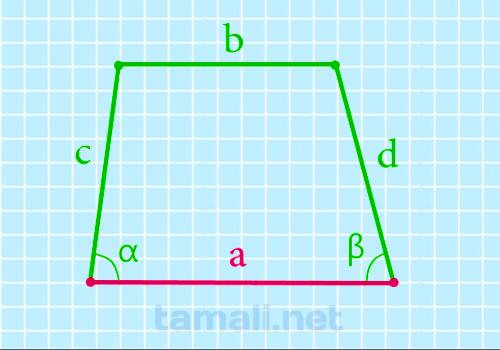
Для нахождения основы а нужно к основе b прибавить произведение одной и другой стороны и косинусов
углов при них
a = b + c * cos α + d * cos β
Цифр после
запятой:
Результат в:
Дана равнобокая трапеция с верхним основанием 6, боковыми сторонами 5 и 11 и углами в 45 градусов.
Найти нижнее основание: а = 6 + 5*2/2 + 11*2/2 = 6 + 162/2 = 6 + 82
Отдельно для подобного типа фигур было выведено два выражения: a = (d1^2 – c^2)/b и a = b +
2c*cosa.
- трапеции ABCD AB = CD = 8, диагональ AC = 12, а BC = 4. Вычислить AD: AD = (12*12 – 8*8)/4
= (144 – 64)/4 = 20 - В трапеции KLMN KL = MN = 4, LM = 7, а LKN равен 30 градусам. Вычислить KN: KN = 7 +
4*2*3/2 = 7 + 43
Верхнее основание через боковые стороны, нижнее основание и углы при нем
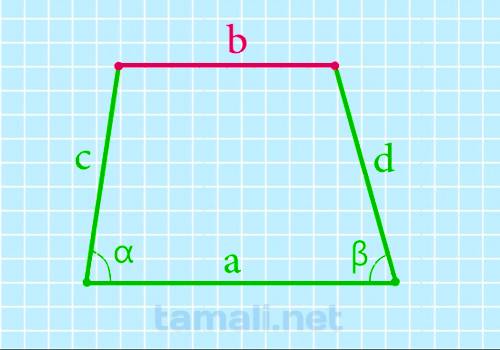
Для нахождения основы b нужно из основы а вычесть произведение одной и другой боковой стороны и углов
при них
b = a – c * cos α – d * cos β
Цифр после
запятой:
Результат в:
Дана трапеция с нижним основанием 27, боковыми сторонами 20 и 14 и углами в 30 и 60 градусов. Найти
верхнее основание: b = 27 — 20*3/2 — 14*1/2 = 27 — 103 — 7 = 20 —
103. Формулы для равнобедренного типа: b = (d1^2 — c^2)/a и b = a — 2c*cosa.
- В трапеции DEFG DE и FG = 11, диагональ АС = 13, а EF = 12. Вычислить DG: DG = (13*13 –
11*11)/12= (169 – 121)/12 = 4 - Боковые стороны трапеции BCDE BC и DE = 25, BE = 10, а CBE равен 60 градусам. Вычислить CD:
CD = 25 – 10*2*1/2 = 15
Боковая сторона через высоту и угол при нижнем основании
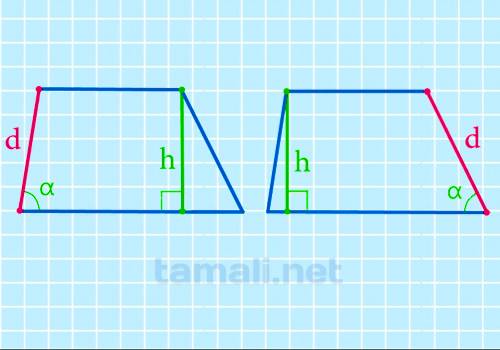
Чтобы найти боковую сторону, надо разделить высоту на синус угла при ней
d = h / sin α
Цифр после
запятой:
Результат в:
Дана трапеция с высотой 12 и углами в 30 и 60 градусов. Найти боковые стороны: c = 12/0,5 =
24, d = 12/3/2 = 243
Для прямоугольного типа формулы несколько отличаются. Самая простая из них связывает высоту и меньшую
боковую сторону: c = h.
Для нее существует еще несколько формул: с = d*sina; c = (a – b)*tga; c
= (d^2 – (a – b)^2)
- В прямоугольной трапеции CDEF сторона EF равна 22, а прилежащий угол = 45. Найти CD. CD =
22*2/2 = 112 - Прямоугольная трапеция MNOP имеет основания MP и NO, равные 32 и 19 соответственно. NMP равен 60
градусам. Найти MP: MP = (32 – 19)*3 = 133 - В прямоугольной трапеции ABCD AD и BC равны 35 и 15 соответственно. Диагональ АС = 26. Найти AB.
AB = (26^2 – (35 – 15)^2) = 676 – 400 = 276 = 269
Первая вытекает из прямоугольного треугольника и свидетельствует о том, что отношение катета к
гипотенузе равно синусу противолежащего угла. В этом треугольнике второй катет равен разности двух
оснований. Отсюда возникает утверждение, приравнивающее тангенс угла к отношению катетов. Третья
формула выведена на основании теоремы Пифагора.
Для второй боковой стороны выведено и записано три выражения: d = (a — b)/cosa; d = c/sina; d =
(c^2 — (a — b)^2). Первое и второе получаются из соотношения сторон в прямоугольном
треугольнике, а третье выводится из теоремы Пифагора.
- В прямоугольной трапеции KLMN KN = 28, LM = 13 а прилежащий угол = 30. Найти KL: KL = (28 –
13)/3/2 = 103 - В прямоугольной трапеции EFGH EF равна 45. FEH равен 30 градусам. Найти GH: GH = 45/0,5 =
90 - В прямоугольной трапеции NOPQ NQ и OP =.36 и 17. Диагональ равна 29. Найти NO: NO = (29^2 –
(36 – 17)^2) = 841 – 361= 480 = 430
Для равнобокой трапеции существуют формулы c = d1^2 – ab; c = (a – b)/2cosa; c = S/m*sina; c =
2S/(a+b)*sina.
- В трапеции LMNO LM = NO. LO = 16, MN = 6, диагональ равна 10. Найти LM: LM = 10^2 – 16*6 =
100 – 96 = 4 - Трапеция ABCD – равнобокая, AB = CD. AD = 18, BC = 4, а прилежащий угол равен 45 градусам. Найти
AB: AB = (18 – 4)/2/2 = 14/2/2 = 14/2 - В трапеции BCDE BC=DE. Площадь фигуры равна 48, BE = 17, CD = 7, а CBE равен 30 градусам.
Вычислить BC: m = (17 – 7)/2 = 5, BC = 48/5*1/2 = 96/5 = 19,2 - Площадь равнобедренной трапеции KLMN = 90, основания KN и LM = 32 и 18 соответственно, а LKN =
60 градусов. Вычислить KL: KL = 2*90/(32 + 18)*3/2 = 360/503 = 129600/7500 = 17,28
Виды трапеций
Существуют следующие виды трапеций:
- Равнобедренная трапеция — фигура, у которой боковые стороны и углы при основании равны.
Диагонали также равны. Треугольники, образованные диагоналями и основой, являются
равнобедренными. Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб. - Прямоугольная трапеция — фигура, у которой одна из боковых сторон перпендикулярна основам
и равна высоте. Два угла будут равны 90 градусам, и они всегда принадлежат смежным вершинам, а
другие всегда острый и тупой, их сумма всегда будет равна 180 градусам. Каждая диагональ
образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из
вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, другая прямоугольный
треугольник. - Разносторонняя трапеция — фигура, боковые стороны которой не равны и углы при основании не
являются прямыми. Ее диагонали делят фигуру на четыре треугольника, два из которых подобны, а
остальные — равновелики, то есть имеют одинаковые площади. Сумма углов при боковой стороне 180
градусов.
Свойства трапеции
- Средняя линия параллельна основаниям и равна их полусумме.
- Любая биссектриса, выведенная из угла четырёхугольника, отсекает на основании (продолжении)
отрезок с длиной боковой стороны. - Треугольники AOD и COD, образованные отрезками диагоналей и основами, подобны.
Коэффициент
подобия – k = AD/BC.
Отношение площадей треугольников — k^2. - Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами, имеют одинаковую
площадь. - В трапецию можно вписать окружность, если сумма оснований равняется сумме её боковых сторон.
- Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений
боковых сторон лежат на одной прямой. - Отрезок, соединяющий середины диагоналей, равняется половине разности основ и лежит на средней
линии.
Amaxar 777
Высший разум
(105180)
4 года назад
Меньшее основание: c1 = a
Большее основание: c2 = a + 2b
Тогда разность оснований: c2 – c1 = (a+2b)-a = 2b
Тогда: b = (c2-c1)/2
b – катет прямоугольного треугольника, прилежащий к острому углу, боковая сторона X – гипотенуза.
cos(ф) = b/X
X = b/cos(ф)
Т. к. sin(ф) ^2 + cos(ф) ^2 = 1:
cos(ф) = sqrt(1 – sin(ф) ^2) = sqrt(1 – 9/25) = 4/5
Тогда X = 5 b / 4
Или X = 5 (c2 – c1) / 8
Дарья БрантУченик (150)
4 года назад
Спасибо))) мне очень помогла особенно формула Х=b/cos(ф)

Нахожу основание АЕ треугольника АЕВ. АЕ = (AD – ВС)/2 = (12 – 6)/2 = 6/2 = 3.
Чтобы найти гипотенузу, АВ в треугольнике АЕВ нужен не синус, а косинус. То есть отношение прилежащей стороны к гипотенузе, а не противолежащей. Смотрим на мой скрин ниже про определения. Вычисляю по формулам:

Мне нужен косинус, а не синус. Вычисляю:
sin²α + cos²α = 1.
cosα = √(1 – sin²α).
cosα = √(1 – 0,8²) = √(1 – 0,64) = √0,36 = 0,6.
Теперь вычисляю гипотенузу по косинусу угла:
3*10/6 = 5 ед.
Мой ответ: Боковая сторона равна 5-ти условным единицам.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,658 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,962 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
1. Формулы длины диагонали равнобедренной трапеции через ее стороны
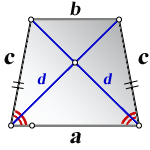
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагональ трапеции
Формула диагонали трапеции (d ):

2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов
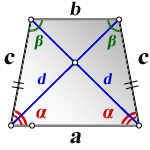
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α, β – углы трапеции
d – диагональ трапеции
Формулы диагонали трапеции (d ):
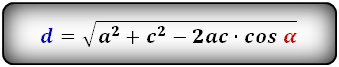
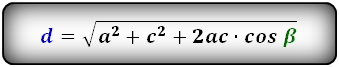
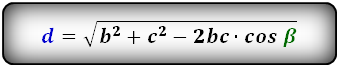
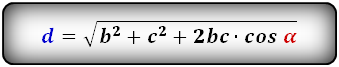
3. Формула длины диагонали равнобедренной трапеции
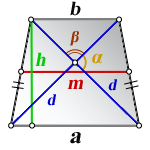
a – нижнее основание
b – верхнее основание
α, β – углы между диагоналями
h – высота трапеции
m – средняя линия трапеции
S – площадь трапеции
d – диагональ трапеции
Формулы диагонали трапеции (d ):

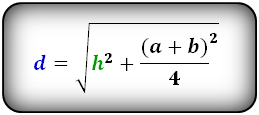
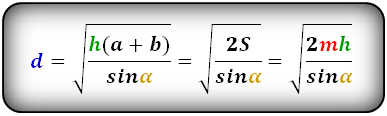
Справедливо для данного случая :
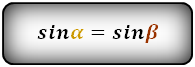
4. Формулы длины диагонали трапеции через высоту и стороны
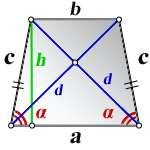
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
h – высота трапеции
α – угол при нижнем основании
d – диагональ трапеции
Формулы диагонали трапеции (d ):
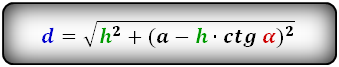
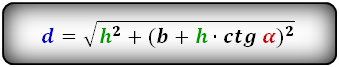

Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
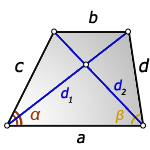
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:
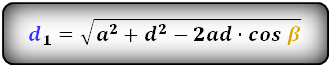
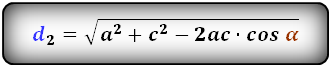
Формулы диагоналей трапеции через четыре стороны:
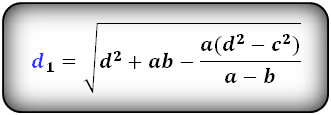

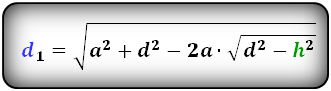
2. Формула длины диагоналей трапеции через высоту
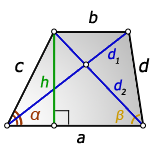
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции через высоту:


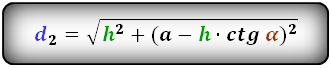


3. Формула длины диагонали трапеции через другую диагональ
a – нижнее основание
b – верхнее основание
α, β – углы между диагоналями
h – высота трапеции
m – средняя линия трапеции
S – площадь трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции :
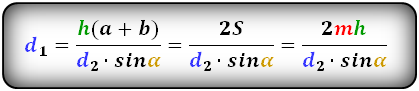
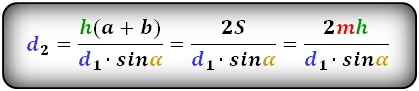
Справедливо для данного случая :
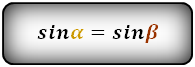
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
d1 , d2 – диагонали трапеции
Формула суммы квадратов диагоналей :
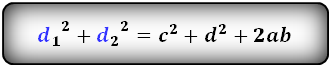
Формулы диагоналей трапеции :
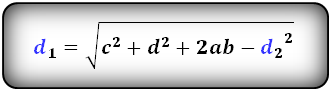
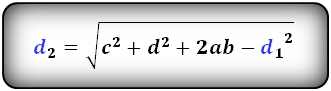
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула средней линии трапеции через основания (для всех видов трапеции)
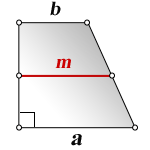
a – нижнее основание
b – верхнее основание
m – средняя линия
Формула средней линии, (m ):
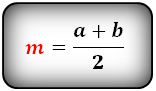
2. Формулы средней линии через основания, высоту и угол при нижнем основании
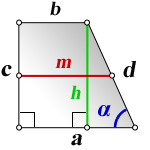
a, b – основания трапеции
c – боковая сторона под прямым углом к основаниям
d – боковая сторона
α – угол при основании
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
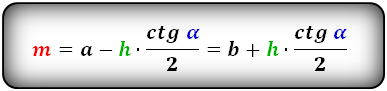
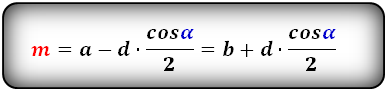
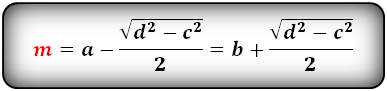
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
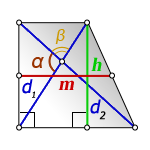
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
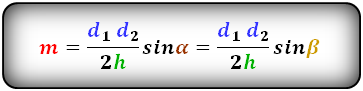
4. Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)
S – площадь трапеции
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m ):
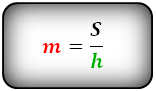
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании
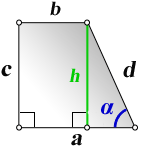
a – нижнее основание
b – верхнее основание
d – боковая сторона
α – угол при нижнем основании
h – высота трапеции
c – боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с) :

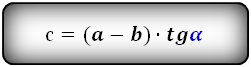
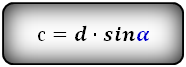
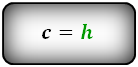
2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
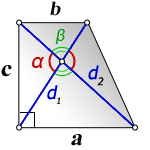
a – нижнее основание
b – верхнее основание
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
c – боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с):
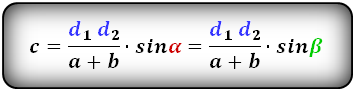
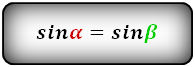
3. Формулы боковой стороны (с) прямоугольной трапеции через площадь
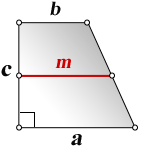
a – нижнее основание
b – верхнее основание
m – средняя линия трапеции
c – боковая сторона под прямым углом к основаниям
Формула длины боковой стороны (с) :
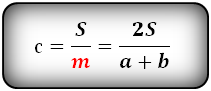
4. Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
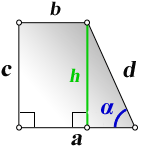
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
α – угол при нижнем основании
h – высота трапеции
d – боковая сторона
Формулы длины боковой стороны (d) :

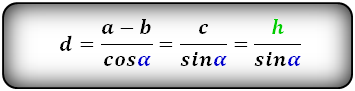
5. Формула боковой стороны (d) прямоугольной трапеции через площадь
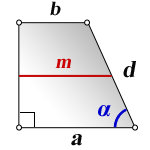
a – нижнее основание
b – верхнее основание
m – средняя линия трапеции
α – угол при нижнем основании
d – боковая сторона
Формула длины боковой стороны (d) :
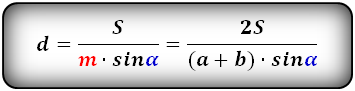
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
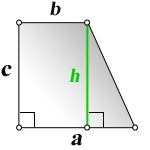
1. Формула длины оснований прямоугольной трапеции через среднюю линию
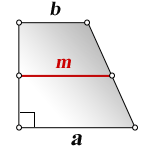
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины оснований :
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
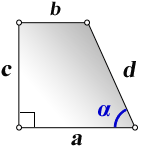
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α – угол при нижнем основании
Формулы длины оснований :
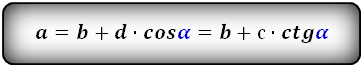
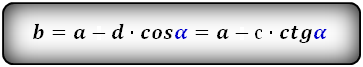
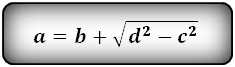

3. Формулы длины оснований трапеции через диагонали и угол между ними
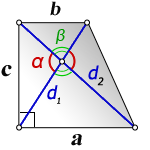
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
Формулы длины оснований :
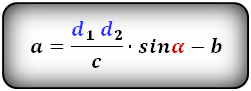
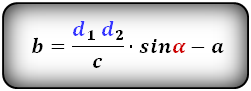
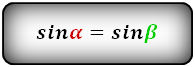
4. Формулы длины оснований трапеции через площадь
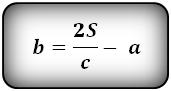
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
h – высота трапеции
Формулы длины оснований :
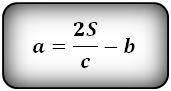
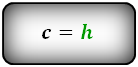
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула средней линии равнобедренной трапеции через основания
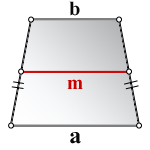
a – нижнее основание
b – верхнее основание
m – средняя линия
Формула средней линии, (m ):
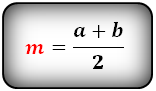
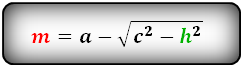
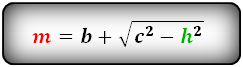
2. Формулы средней линии через основание, высоту и углы при нижнем основании
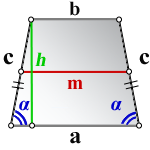
a – нижнее основание
b – верхнее основание
c – боковая сторона
α – угол при нижнем осровании
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
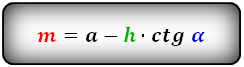
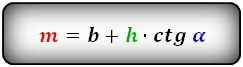
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
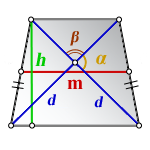
d – диагонали трапеции
α , β – углы между диагоналями
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m ):
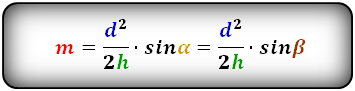
4. Формула средней линии трапеции через площадь и высоту
S – площадь трапеции
h – высота трапеции
α – угол при нижнем осровании
m – средняя линия
Формула средней линии трапеции, (m ):

Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
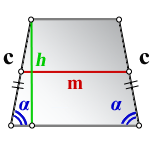
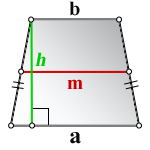
1. Формула высоты равнобедренной трапеции через стороны и углы при основании
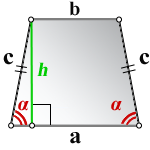
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при нижнем основании
h – высота трапеции
Формулы длины высоты, (h ):

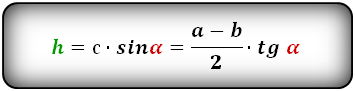
2. Формула высоты равнобедренной трапеции через диагонали и углы между ними
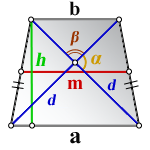
d – диагонали трапеции
α , β – углы между диагоналями
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
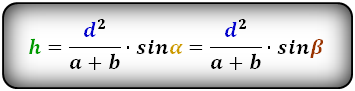
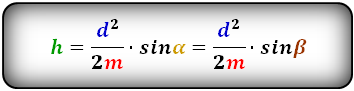
3. Формула высоты равнобедренной трапеции через площадь
S – площадь трапеции
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
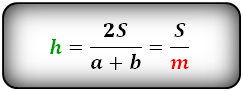
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины основания равнобедренной трапеции через среднюю линию
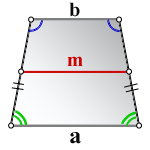
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины основания:
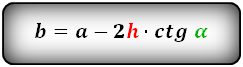
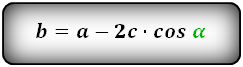
2. Формулы длины сторон через высоту и угол при нижнем основании
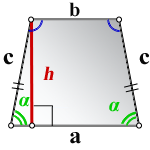
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при основании трапеции
h – высота трапеции
Формулы всех четырех сторон трапеции:
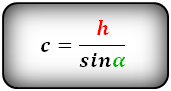
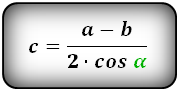
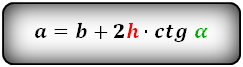
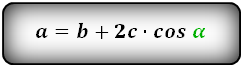
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
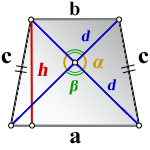
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагонали
α , β – углы между диагоналями
h – высота трапеции
Формулы длины сторон трапеции:
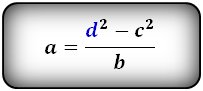
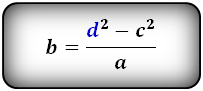

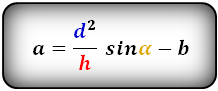
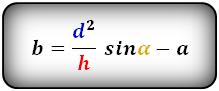
справедливо для данной ситуации:
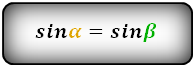
4. Формулы длины сторон равнобедренной трапеции через площадь
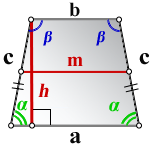
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α , β – углы при основаниях
m – средняя линия
h – средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
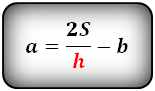
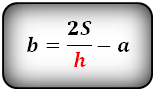
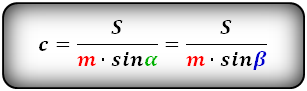

Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются – верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
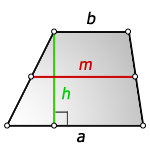
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
1. Формула высоты трапеции через стороны и углы при основании
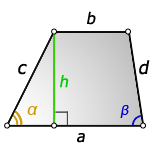
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
Формулы длины высоты, (h ):
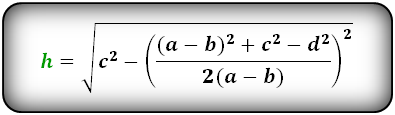
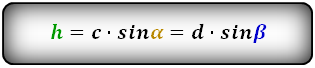
2. Формула высоты трапеции через диагонали и углы между ними
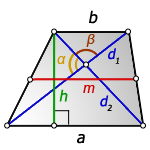
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
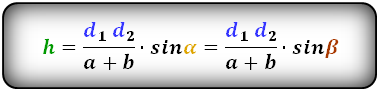
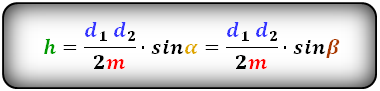
3. Формула высоты трапеции через площадь
S – площадь трапеции
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
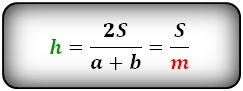
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются – верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции – отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
1. Формула средней линии трапеции через основания
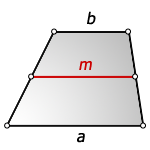
b – верхнее основание
a – нижнее основание
m– средняя линия
Формула средней линии, (m ):
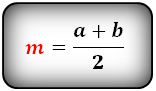
2. Формулы средней линии через основание, высоту и углы при нижнем основании
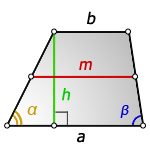
b – верхнее основание
a – нижнее основание
α, β – углы трапеции
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m):
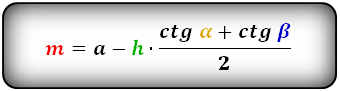
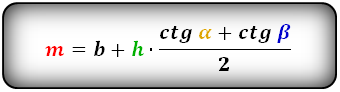
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
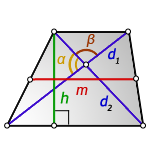
α, β – углы между диагоналями
d1 , d2 – диагонали трапеции
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
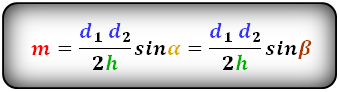
4. Формула средней линии трапеции через площадь и высоту
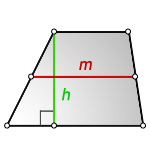
S – площадь трапеции
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m):
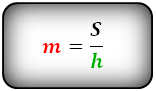
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины основания трапеции через среднюю линию
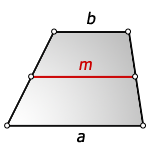
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины оснований :


2. Формулы длины сторон через высоту и углы при нижнем основании
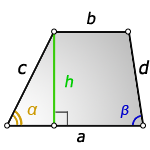
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
Формулы всех четырех сторон трапеции:



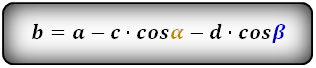
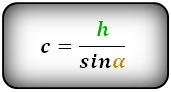
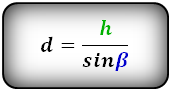
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
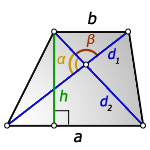
a – нижнее основание
b – верхнее основание
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
h – высота трапеции
Формулы длины сторон трапеции:
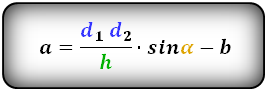
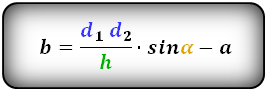
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии

