Как найти боковую сторону усеченного конуса - Сайт, где вы сможете решить свои вопросы

Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту

Формулы усеченного конуса

Для расчёта всех основных параметров усеченного конуса воспользуйтесь калькулятором.

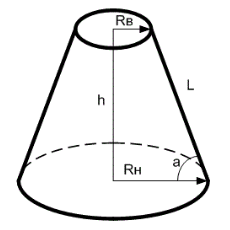
Объём усеченного конуса

$$
V = {1 over 3} * pi * h * (R_Н^2 + R_Н * R_В + R_В^2)
$$

Площадь боковой поверхности усечённого конуса

$$
S_Б = pi * (R_Н + R_В) * L
$$

Высота усеченного конуса через образующую и радиусы оснований

$$
h = sqrt{L^2 – (R_Н – R_В)^2}
$$

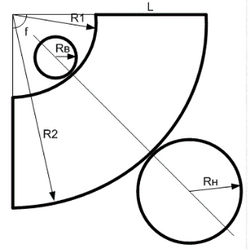
Развертка (выкройка) усеченного конуса

Длина образующей, L

$$
L = sqrt{(R_Н – R_В)^2 + h^2}
$$
$$
R_1 = {L * R_В over R_Н – R_В}
$$
$$
R_2 = L + R_1
$$

Угол ∠ f

$$
∠ f = 360° * {R_Н – R_В over L}
$$

Источник

Площадь поверхности усеченного конуса

Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.

Усечённый конус может быть получен вращением прямоугольной трапеции вокруг меньшей боковой стороны.

Формула площади боковой поверхности усеченного конуса: S = π l (R + r) ,

где R – радиус нижнего основания, r – радиус верхнего основания, l – образующая усеченного конуса.

Формула площади полной поверхности усеченного конуса: S = π (l R + l r + R² + r²) ,

где R – радиус нижнего основания, r – радиус верхнего основания, l – образующая усеченного конуса.

Образующая усеченного конуса рассчитывается по формуле:

,
где R – радиус нижнего основания, r – радиус верхнего основания, h – высота усеченного конуса.

Калькулятор пощади поверхности усеченного конуса позволяет найти площадь боковой поверхности усеченного конуса и полную площадь поверхности усеченного конуса.

Поделиться страницей в социальных сетях:

Источник

Введение

Рис. 1. Предметы из жизни, имеющие форму усеченного конуса

Как вы думаете, откуда в геометрии берутся новые фигуры? Все очень просто: человек в жизни сталкивается с похожими объектами и придумывает, как бы их назвать. Рассмотрим тумбу, на которой сидят львы в цирке, кусок морковки, который получается, когда мы нарезали только часть ее, действующий вулкан и, например, свет от фонарика (см. рис. 1).

Усеченный конус, его элементы и осевое сечение

Рис. 2. Геометрические фигуры

Мы видим, что все эти фигуры похожей формы – и снизу, и сверху они ограничены кругами, но они сужаются кверху (см. рис. 2).

Рис. 3. Отсечение верхней части конуса

Это похоже на конус. Только не хватает верхушки. Мысленно представим, что мы берем конус и отсекаем от него верхнюю часть одним взмахом острого меча (см. рис. 3).

Рис. 4. Усеченный конус

Получается как раз наша фигура, называется она усеченный конус (см. рис. 4).

Рис. 5. Сечение, параллельное основанию конуса

Пусть дан конус. Проведем плоскость, параллельную плоскости основания этого конуса и пересекающую конус (см. рис. 5).

Она разобьет конус на два тела: одно из них – конус меньшего размера, а второе и называется усеченным конусом (см. рис. 6).

Рис. 6. Полученные тела при параллельном сечении

Таким образом, усеченный конус – это часть конуса, заключенная между его основанием и параллельной основанию плоскостью. Как и в случае с конусом, усеченный конус может иметь в основании круг – в этом случае его называют круговым. Если исходный конус был прямым, то и усеченный конус называют прямым. Как и в случае с конусами, мы будем рассматривать исключительно прямые круговые усеченные конусы, если специально не указано, что речь идет о непрямом усеченном конусе или в его основаниях не круги.

Рис. 7. Вращение прямоугольной трапеции

Наша глобальная тема – тела вращения. Усеченный конус – не исключение! Вспомним, что для получения конуса мы рассматривали прямоугольный треугольник и вращали его вокруг катета? Если полученный конус пересечь плоскостью, параллельной основанию, то от треугольника останется прямоугольная трапеция. Ее вращение вокруг меньшей боковой стороны и даст нам усеченный конус. Заметим снова, что речь, разумеется, идет только о прямом круговом конусе (см. рис. 7).

Рис. 8. Основания усеченного конуса

Сделаем несколько замечаний. Основание полного конуса и круг, получающийся в сечении конуса плоскостью, называют основаниями усеченного конуса (нижним и верхним) (см. рис. 8).

Рис. 9. Образующие усеченного конуса

Отрезки образующих полного конуса, заключенные между основаниями усеченного конуса, называют образующими усеченного конуса. Так как все образующие исходного конуса равны и все образующие отсеченного конуса равны, то и образующие усеченного конуса равны (не путать отсеченный и усеченный!). Отсюда и следует равнобедренность трапеции осевого сечения (см. рис. 9).

Отрезок оси вращения, заключенный внутри усеченного конуса, называют осью усеченного конуса. Этот отрезок, разумеется, соединяет центры его оснований (см. рис. 10).

Рис. 10. Ось усеченного конуса

Высота усеченного конуса – это перпендикуляр, проведенный из точки одного из оснований к другому основанию. Чаще всего, в качестве высоты усеченного конуса рассматривают его ось.

Рис. 11. Осевое сечение усеченного конуса

Осевое сечение усеченного конуса – это сечение, проходящее через его ось. Оно имеет вид трапеции, чуть позже мы докажем ее равнобедренность (см. рис. 11).

Площади боковой и полной поверхностей усеченного конуса

Рис. 12. Конус с введенными обозначениями

Найдем площадь боковой поверхности усеченного конуса. Пусть основания усеченного конуса имеют радиусы и , а образующая равна (см. рис. 12).

Рис. 13. Обозначение образующей отсеченного конуса

Найдем площадь боковой поверхности усеченного конуса как разность площадей боковых поверхностей исходного конуса и отсеченного. Для этого обозначим через образующую отсеченного конуса (см. рис. 13).

Тогда искомая .

Рис. 14. Подобные треугольники

Осталось выразить .

Заметим, что из подобия треугольников , откуда (см. рис. 14).

Можно было бы выразить , разделив на разность радиусов, но нам это не нужно, ведь в искомом выражении как раз фигурирует произведение . Подставив вместо него , окончательно имеем: .

Несложно теперь получить и формулу для площади полной поверхности. Для этого достаточно добавить площади двух кругов оснований: .

Задача

Рис. 15. Иллюстрация к задаче

Пусть усеченный конус получен вращением прямоугольной трапеции вокруг ее высоты . Средняя линия трапеции равна , а большая боковая стороны – (см. рис. 15). Найти площадь боковой поверхности полученного усеченного конуса.

Решение

По формуле мы знаем, что .

Образующей конуса будет являться большая сторона исходной трапеции, то есть Радиусы конуса – это основания трапеции. Найти их мы не можем. Но нам и не надо: нужна лишь их сумма, а сумма оснований трапеции вдвое больше ее средней линии, то есть она равна . Тогда .

Ответ: .

Сходство усеченных конуса и пирамиды

Обратите внимание, что, когда мы говорили о конусе, мы проводили параллели между ним и пирамидой – формулы были аналогичными. Так же и здесь, ведь усеченный конус очень похож на усеченную пирамиду, так что формулы для площадей боковой и полной поверхностей усеченного конуса и пирамиды (а скоро будут и формулы для объема) аналогичны.

Задача

Рис. 1. Иллюстрация к задаче

Радиусы оснований усеченного конуса равны и , а образующая равна . Найти высоту усеченного конуса и площадь его осевого сечения (см. рис. 1).

Решение

Рассмотрим осевое сечение, это трапеция , основания которой – удвоенные радиусы ( и ), а боковая сторона равна образующей () (см. рис. 2).

Рис. 2. Иллюстрация к задаче

Проведем высоту . Отрезок равен полуразности оснований, значит, он равен . Тогда треугольник подобен египетскому, а значит, . Высоту усеченного конуса мы нашли.

А площадь осевого сечения – это просто площадь трапеции, она равна произведению полусуммы оснований () на высоту (), то есть .

Ответ: ,

Список рекомендованной литературы

Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.
Геометрия 11 класс, А.В. Погорелов, М.: Просвещение, 2002
Рабочая тетрадь по геометрии 11 класс, В.Ф. Бутузов, Ю.А. Глазков

Рекомендованные ссылки на ресурсы сети Интернет

2mb.ru (Источник).
Math24.ru (Источник).
Igspl.na.by (Источник).

Домашнее задание

Высота усеченного конуса равна , а угол между образующей и плоскостью большего основания равен . Найдите образующую усеченного конуса.
Радиусы оснований усеченного конуса относятся как . Найдите площадь осевого сечения усеченного конуса, если его высота равна , а образующая – .
Площади оснований усеченного конуса равны и . Через середину его высоты проведено сечение, параллельное основаниям. Найдите площадь этого сечения.

Источник

Усеченный конус – это часть конуса, ограниченная между двумя параллельными основаниями перпендикулярными его оси симметрии.Основаниями конуса являются геометрические круги.

Усеченный конус может быть получен в результате вращения прямоугольной трапеции вокруг ее боковой стороны, которая является ее высотой. Границей конуса является круг радиуса R, круг радиуса r и боковая поверхность конуса. Боковую поверхность конуса описывает боковая сторона трапеции во время ее вращения.

Площадь боковой поверхности усеченного конуса через направляющую и радиусы его оснований

При нахождении площади боковую поверхность усеченного конуса целесообразней рассматривать как разность боковой поверхности конуса и боковой поверхности отсеченного конуса.

Пусть от данного конуса AMB отсекли конус A`MB`. Необходимо вычислить боковую площадь усеченного конуса AA`B`B. Известно, что радиусы его оснований AO=R, A`O`=r, образующая равна L.Обозначим MB` за x. Тогда боковая поверхность конуса A`MB` будет равна πrx. А боковая поверхность конуса AMB будет равна πR(L+x).
Тогда боковую поверхность усеченного конуса AA`B`B можно выразить через разность боковой поверхности конуса AMB и конуса A`MB`:
$S_bok={pi}R(L+x)-{pi}rx={pi}(RL+Rx-rx)={pi}(RL+x(R-r))$
Треугольники OMB и O`MB`– подобны по равенству углов ∠{MOB} = ∠{MO`B`} и ∠{OMB} = ∠{O`MB`}. Из подобия этих треугольников следует:
Воспользуемся производной пропорции. Имеем:
Отсюда находим x:
Подставив это выражение в формулу площади боковой поверхности, имеем: $S_bok={pi}(RL+{{rL}/{R-r}} (R-r) )={pi}(RL+rL)={pi}L(R+r)$
Таким образом, площадь боковой поверхности усеченного конуса равна произведению числа π на его направляющую и сумму радиусов его оснований.
Формула площади боковой поверхности усеченного конуса имеет следующий вид: $S_bok={pi}L(R+r)$

Пример расчета площади боковой поверхности усеченного конуса, если известны его радиус и образующая
Радиус большего основания, образующая и высота усеченного конуса равны 7, 5 и 4 см соответственно. Найдите площадь боковой поверхности конуса.
Осевое сечение усеченного конуса представляет собой равнобедренную трапецию, с основаниями 2R и 2r. Образующая усеченного конуса, являющаяся боковой стороной трапеции, высота, опушенная на большое основание и разность радиусов основания усеченного конуса, образуют египетский треугольник. Это прямоугольный треугольник с соотношением сторон 3:4:5. По условию задачи образующая равна 5, а высота – 4, тогда разность радиусов основания усеченного конуса будет равна 3.
Имеем:
L=5
R=7
R=4
Формула площади боковой поверхности усеченного конуса имеет следующий вид:
$S_bok={pi}L(R+r)$
Подставив значения, имеем:
$S_bok=5{pi}(7+4)=27{pi}$

Площади боковой поверхности усеченного конуса через направляющую и средний радиус

Средний радиус усеченного конуса равен половине суммы радиусов его оснований:
$R_sr={R+r}/2$

Тогда формула площади боковой поверхности усеченного конуса может быть представлена следующим образом:
$S_bok=2{pi}LR_sr$
Площадь боковой поверхности усеченного конуса равна произведению длины окружности среднего сечения на его образующую.

Площади боковой поверхности усеченного конуса через радиусы его основания и угол наклона образующей к плоскости основания

Если меньшее основание ортогонально спроектировать на большее основание, то тогда проекция боковой поверхности усеченного конуса будет иметь вид кольца, площадь которого вычисляется по формуле:
$S={pi}(R^2-r^2)={pi}(R-r)(R+r)$
Тогда: $S_bok={{pi}(R-r)(R+r)}/{cos{alpha}}$

Площади боковой поверхности усеченного конуса по Архимеду

$S_bok={pi}(sqrt{L(R+r)})^2$
Площадь боковой поверхности усеченного конуса равна площади такого круга, радиус которого является средней пропорциональной между образующей и суммой радиусов его оснований

Полная поверхность усеченного конуса

Полная поверхность конуса – это сумма площади его боковой поверхности и площади оснований конуса:

$S_poln=S_bok+S_{b.osn}+S_{m.osn}$

Основаниями конуса является круги с радиусом R и r. Их площадь равна произведению числа на квадрат их радиуса:
$S_{b.osn}={pi}R^2$
$S_{m.osn}={pi}r^2$
Площадь боковой поверхности вычисляется по формуле:
$S_bok={pi}L(R+r)$
Тогда площадь полной поверхности усеченного конуса равна:
$S_poln={pi}L(R+r)+{pi}R^2+{pi}r^2={pi}(R^2+(R+r)L+r^2)$
Формула имеет следующий вид:
$S_poln={pi}(R^2+(R+r)L+r^2)$

Пример расчета площади полной поверхности усеченного конуса, если известны его радиус и образующая
Радиус основания усеченного конуса 1 и 7 дм, а диагонали осевого сечения взаимно перпендикулярны. Найдите площадь полную площадь усеченного конуса
Осевое сечение усеченного конуса представляет собой равнобедренную трапецию, с основаниями 2R и 2r. То есть основания трапеции равны 2 и 14 дм соответственно. Так как диагонали трапеции взаимно перпендикулярны, то высота равна полусумме ее оснований. Тогда:

Образующая усеченного конуса, являющаяся боковой стороной трапеции, высота, опушенная на большое основание и разность радиусов основания усеченного конуса, образуют прямоугольный треугольник.
По теореме Пифагора найдем образующую усеченного конуса:
$L=sqrt{h^2+(R-r)^2}=sqrt{8^2+(7-1)^2}=sqrt{64+36}=sqrt{100}=10$
Формула площади полной поверхности усеченного конуса имеет следующий вид:
$S_poln={pi}(R^2+(R+r)L+r^2)$
Подставив значения из условия задачи и найденные значения, имеем:
$S_poln={pi}(7^2+(7+1)10+1^2)={pi}(49+80+1)=130{pi}$