Как найти боковую строну по площади

Как по площади определить стороны

С каждым годом задачи по геометрии становятся сложнее. Уже недостаточно знать, как считать по готовым формулам. Необходимо уметь из уже готовой вывести новую формулу, чтобы узнать ту или иную величину.

Инструкция

Вычисление сторон квадрата. Формула площади квадрата а², где а – сторона данной фигуры. Для вычисления площади квадрата нужно знать лишь одну сторону, так как все его стороны равны. Отсюда вычислить сторону очень просто: √а. Пример: Площадь равна 49. Выделите квадратный корень из 49. Ответ: 7.

Вычисление сторон прямоугольника. Найти стороны этой фигуры, зная лишь значение площади, невозможно. Нужно знать еще одну величину – его периметр. Вот пример, площадь равна 12, а периметр 14.
Обозначьте стороны прямоугольника «х» и «у». Из формулы вычисления периметра P=2(a+b) подставьте значения нашей задачи 2(х+у)=14.
Из формулы вычисления площади S=ab подставьте значения нашей задачи ху=12, т. е. х=12/у. Подставьте значение «х» в уравнение 2(х+у)=14.
Получится 2(12/у+у)=14. Перенесите подобные 12/y+y=14/2. 12/у+у=7. Умножьте обе части уравнения на «у». Получится 12+у^2=7у. у^2-7у+12=0 – квадратное уравнение, считайте через дискриминант. У уравнения 2 корня у=4; у=3.
Ответ: стороны прямоугольника равны 3 и 4 см соответственно.

Вычисление сторон ромба. Для того чтобы узнать стороны ромба (EWYP), помимо площади нужно иметь еще какое-нибудь значение. Например, высота – WH, она же длина перпендикуляра, опущенного из вершины (W) на сторону (EP). Следует помнить, что стороны ромба равны между собой. В этом случае очень легко определить сторону ромба (EW). Как известно, ромб можно представить как два треугольника EWP и PWY, площадь каждого из которых равняется половине произведения высоты на основание. Можно сделать вывод, что площадь ромба будет равна произведению высоты на длину стороны. Отсюда получается простая формула для вычисления длины стороны ромбы: нужно его площадь разделить на длину высоты – |EW|=S/|WH|. Пример: Пусть площадь ромба EWYP равна 20. А высота WH=5. Подставьте значения в приведенную формулу: |EW|=20/|5 . Ответ: сторона равна 4.

Вычисление сторон равностороннего треугольника. Для того чтобы узнать его сторону (а все его стороны равны), помимо площади необходимо знать высоту. Если известны две эти величины, то расчет можно совершить по этой формуле: b=2S/h, где b – сторона треугольника, S – площадь, h – высота. Пример: Пусть площадь равностороннего треугольника ABC равна 25. Высота BH = 5.
Подставьте значения в формулу: b=2*25/5. Ответ: сторона равна 10.

Обратите внимание

Расчет сторон остальных фигур, имеющих стороны различные по длине друг к другу, требует знания большего количества величин.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

Как найти сторону треугольника по двум сторонам и площади?

Как найти площадь треугольника если известны две стороны?

Площадь треугольника через две стороны и угол между ними.

S = 0,5 * a * b⋅sin(α) , где a, b — стороны, α — угол между ними.

Как найти длину стороны треугольника?

c 2 = a 2 +b 2 , где a, b — катеты, с — гипотенуза прямоугольного треугольника. После того, как найдены все стороны треугольника, находим его периметр, как сумму двух катетов и гипотенузы.

Как найти третью сторону в равнобедренном треугольнике?

Зная боковую сторону равнобедренного треугольника и угол при основании, можно найти третью сторону. По аналогичному алгоритму можно найти сторону равнобедренного треугольника, зная высоту, но в таком случае половина основания будет равна произведению высоты на синус угла при основании.

Как найти синус угла зная две стороны?

Для этого воспользуйтесь соотношением, указанным ниже:a/sin α=b/sin b=c/sin y=2RЭта теорема применима в том случае, когда известны две стороны и угол треугольника, либо дан один из углов треугольника и радиус описанной вокруг него окружности.

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

[spoiler title=”источники:”]

http://fcessentuki.ru/kak-naiti-storonu-treugolnika-po-dvum-storonam-i-ploshchadi

http://vsvoemdome.ru/obrazovanie/kak-nayti-ploschad-treugolnika

[/spoiler]

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

1. Найти все стороны треугольника.
2. Найти все углы треугольника.
3. Найти площадь (S) и периметр (P) треугольника.
4. Найти радиус (r) вписанной окружности.
5. Найти радиус (R) описанной окружности.
6. Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
 

Сторона треугольника (или длина сторон) может быть найдена различными методами. 
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b – катеты, с – гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b – катеты, с – гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.

​​​​​Для равностороннего треугольника:

1) Найти сторону через площадь

где a – искомая сторона, S – площадь треугольника.

2) Найти сторону через высоту

где a – искомая сторона,h – высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a – искомая сторона,r – радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a – искомая сторона,R – радиус описанной окружности.

​​​​​Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a – искомая сторона, b – известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word

Треугольником называется фигура, которая состоит их трех точек (вершины), которые не лежат на одной
прямой и трех попарно соединяющих эти точки отрезков (стороны). Треугольники бывают остроугольными,
тупоугольными, прямоугольными, равнобедренными, равносторонними, разносторонними. С данной фигурой
связано много формул, теорем, правил. Ниже приведены формулы и примеры по нахождению стороны
треугольника.

Сторона равностороннего треугольника через радиус описанной окружности

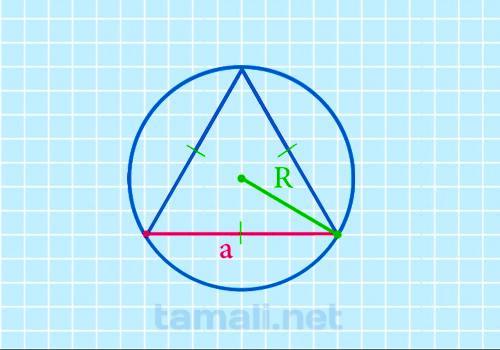
Для того чтобы найти сторону равностороннего треугольника через радиус описанной окружности
необходимо ее радиус умножить на корень квадратный из трех. Таким образом, формула будет выглядеть
следующим образом:

a = R * √3

где а — сторона треугольника, R — радиус описанной окружности.

Пример. Пусть дан равносторонний треугольник с радиусом описанной окружности 10см. Подставим в
формулу и получится: a = 10*√3 = 10 * 1,732 ≈ 17,3 см.

Сторона равностороннего треугольника через радиус вписанной окружности

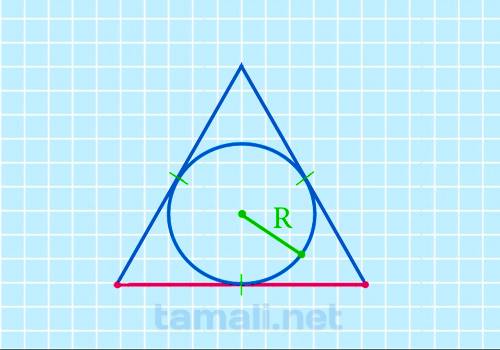
Для нахождения стороны правильного треугольника через радиус вписанной окружности следует
использовать формулу радиуса r= a (√3 / 6). Отсюда можно вывести формулу следующим образом: a = r (6
/ √3) = r *(6√3 / √3√3) = r * (6√3 / 3). Формула будет следующая (удвоенный радиус умножить на
квадратный корень из трех):

a = 2r * √3

где а — сторона треугольника, R — радиус вписанной окружности.

Пример. Пусть дан равносторонний треугольник с радиусом вписанной окружности 23см. Подставим в
формулу и получится: a = 2 * 23 * √3 = 2 * 23 * 1,732 ≈ 79,7см.

Сторона равностороннего треугольника через высоту

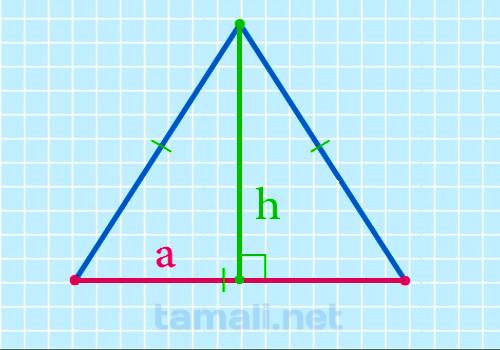
Для того чтобы найти сторону равностороннего треугольника через высоту следует применить теорему
Пифагора. Сторона равностороннего треугольника a² будет равна сумме квадратов высоты и половины
основания, которое также является стороной a: a² = h² + (a/2)² ⇒ a² = h² + a²/4 ⇒ a² — a²/4
=h² ⇒ (4a² — a²) / 4 = h² ⇒ 3a²/4 = h² ⇒ a² = 4*h²/3 ⇒a = √(4h²/3). Отсюда можно вывести
формулу для нахождения стороны через высоту:

a = 2h / √3

где а — сторона, h —  высота равностороннего треугольника.

Пример. Пусть дан равносторонний треугольник с высотой 45см. Подставим в формулу и получится: a = 2 *
45 / √3 = 2 * 45 / 1,732 ≈ 51,963 см.

Сторона равностороннего треугольника через площадь

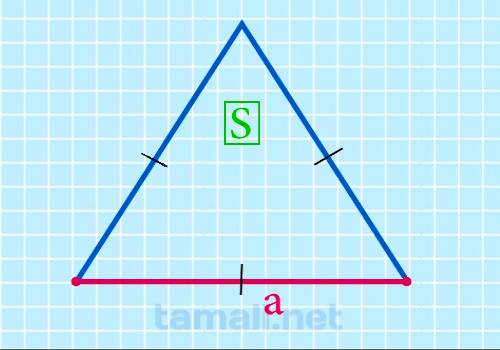
Для того чтобы найти сторону равностороннего треугольника через площадь нужно применить следующую
формулу

a = √(4S / √3)

где а — сторона, S —  площадь равностороннего треугольника.

Пример. Пусть дан равносторонний треугольник с площадью 64м². Подставим в формулу и получится: a =
√(4*64 / √3)= √(4 * 64 / 1,732) ≈ 12,157 см.

Основание равнобедренного треугольника через боковые стороны и угол между ними

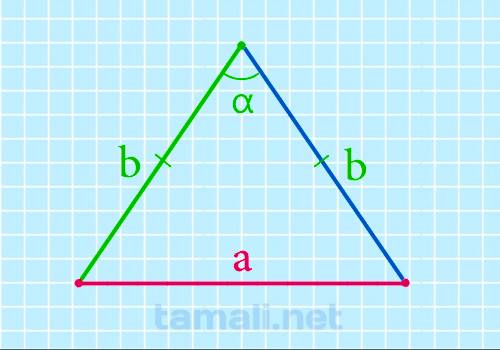
Равнобедренным называется треугольник, у которого есть две равные стороны, называемые ребрами, а
третья сторона основанием. Для того чтобы найти основание нужно знать или один из углов, или высоту
треугольника, приводящаяся к основанию. Его можно вычислить по данной формуле:

a = 2b * sin (α/2)

где a — длина основания треугольника, b — длина стороны треугольника; α — это угол,
который противоположен основанию.

Пример. Если сторона a = 10 см, а ∠β = 12°, то: a = 2⋅10⋅sin 12/2 = 2⋅10⋅0,1045 =2,09 см.

Основание равнобедренного треугольника через боковые стороны и угол при основании

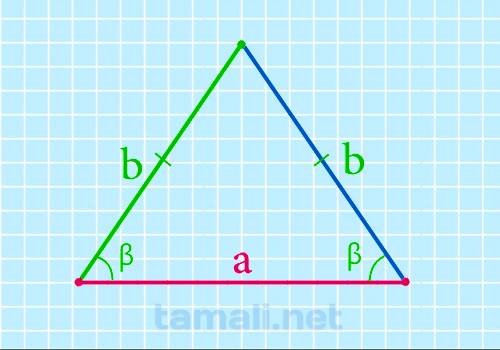
Угол при основании равнобедренного треугольника равен разности 90º и половины угла при его вершине и
чем больше угол при вершине равнобедренного треугольника, тем он меньше. Может быть только острым,
то есть прямым или тупым он быть не может. Если известен угол при основании и боковые стороны, то
можно найти основание равнобедренного треугольника по следующей формуле:

a = 2b + cos β

где b — боковая сторона, β — угол при основании.

Пример. Если сторона a = 10 см, а ∠β = 40°, то: a = 2⋅10⋅cos 40 = 2⋅10⋅0,766 =15.32 см.

Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами

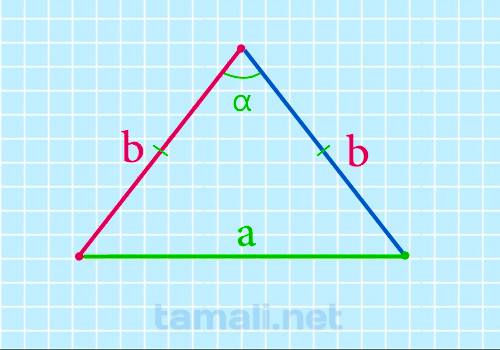
В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны,
из чего можно сделать вывод что если углы при основании треугольника одинаковы по значению, значит
он является равнобедренным.  Это значит, что α = β.

Формула, выражающая боковую сторону равнобедренного треугольника через основание и угол боковыми
сторонами:

b = a / (2 * sin(α/2))

где d — основание равнобедренного треугольника, α — угол между боковыми сторонами.

Пример. Если сторона a = 17 см, а ∠α = 50°, то: a = 17 / 2 * sin (50/2) = 17 / 2 * sin 25 = 20.11
см.

Боковая сторона равнобедренного треугольника через основание и угол при основании

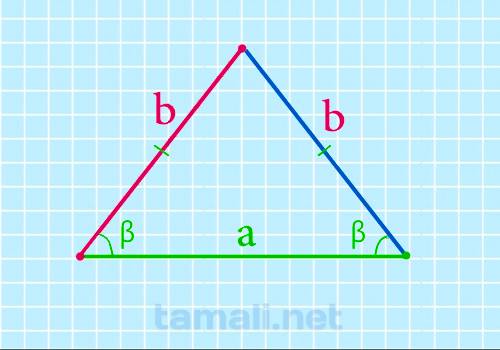
Если известно основание и угол при нем, то формула боковой стороны равнобедренного треугольника будет
выглядеть следующим образом:

b = a / 2 * cos β

где a — это основание, β — угол при основании равнобедренного треугольника.

Здесь длина боковых сторон будет равно b: AB=BC=b, длина основания a: AC=a. Для доказательства
формулы боковой стороны применяется теорема косинусов, вернее, ее следствие.

Пример. Пусть основание (a) равно 35мм, а угол β — 60º, тогда подставив в формулу получим b =
35 / 2 * 0,5=35 мм.

Катет прямоугольного треугольника через гипотенузу и острый угол

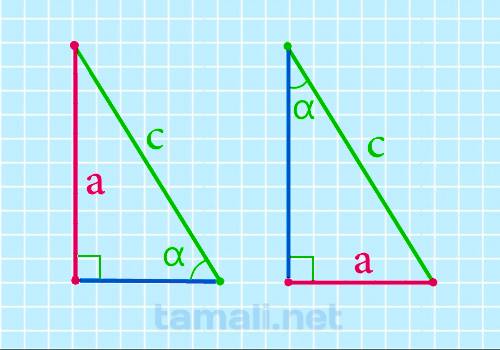
Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом: катет,
противолежащий углу α, равен произведению гипотенузы на sin α, то есть формула будет выглядеть
следующим образом:

a = c * sin α

где c — гипотенуза, α — острый угол прямоугольного треугольника.

Пример. Пусть гипотенуза с равна 77см, а острый угол 80º, тогда подставив в формулу значения получим
следующее:  a = 77 * 0,98 = 75,8см.

Катет прямоугольного треугольника через гипотенузу и другой известный катет

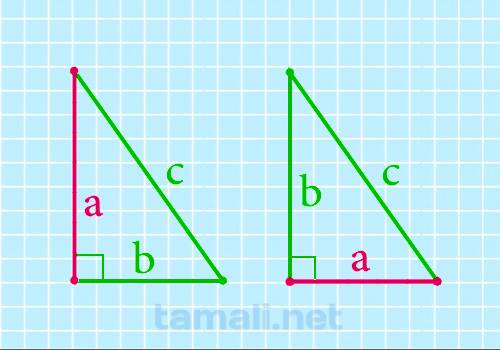
Если известен один катет и гипотенузу, то можно найти другой катет. Для этого необходимо
воспользоваться формулой:

a = √(c² — b²)

где c — гипотенуза, b — катет который известен прямоугольного треугольника.

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а
катет b = 4 см: a = √(5² — 4)² = √(25 — 16) = √9 = 3 см

Гипотенуза прямоугольного треугольника через катет и острый угол

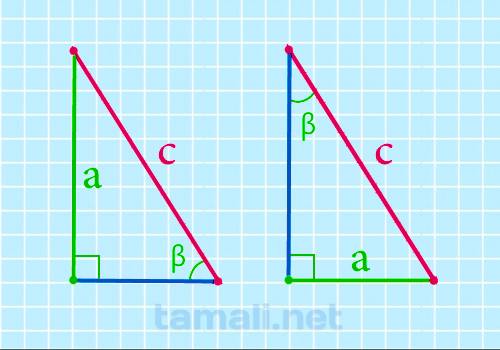
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему
угол можно узнать по формуле:

c = a / sin(β)

где a — катет, β — острый угол прямоугольного треугольника.

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 4 см, а
противолежащий к нему ∠β =60°: c = 4 / sin(60) = 4 / 0,87 = 8,04 см.

Гипотенуза прямоугольного треугольника через катеты

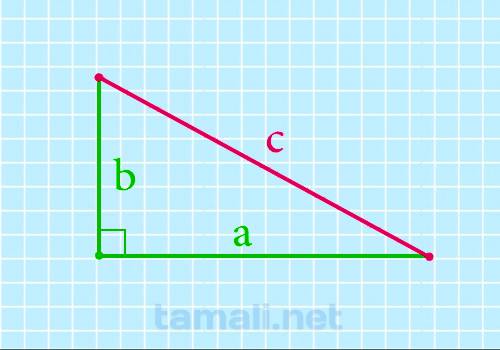
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b) можно рассчитать по
формуле используя теорему Пифагора. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов
катетов: c² = a² + b² следовательно:

c = √(a² + b²)

где c — гипотенуза, a и b — катеты.

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет
b = 4 см: c = √3² + 4² = √9 + 16 = √25 = 5 см

Сторона треугольника через две известные стороны и угол между ними

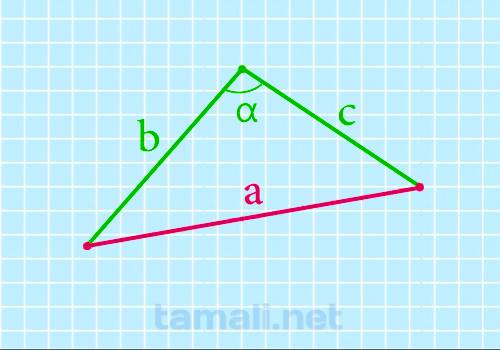
По стороне и двум углам или по двум сторонам и углу можно тоже вычислить длину стороны
треугольника:

a = b² + c² — 2bc * cos α

где a, b, c — стороны произвольного треугольника, α — угол между сторонами который
известен.

Обязательно обратите внимание что при подстановке в формулу, для тупого угла (α>90), cosα
принимает отрицательное значение.

Пример. Пусть сторона с равна 10 см, сторона b — 7, угол α — 60 градусов. Таким образом
получим подставив в формулу:
a = 7² + 10² — 2 * 7 * 10 * cos 60 = 8,89 см.

Сторона треугольника через известную сторону и два угла

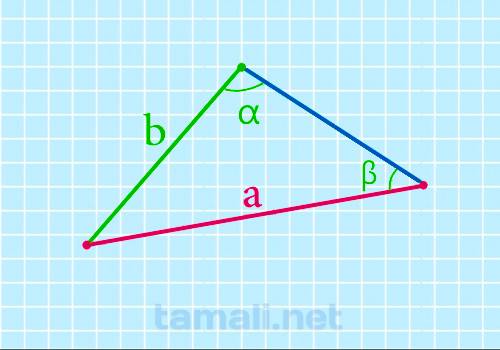
Для нахождения стороны треугольника через известную сторону и два угла необходимо воспользоваться
теоремой синусов и формула будут следующая:

a = (b * sin α) / sin β

где b — сторона треугольника; β, α — углы треугольника.

Пример. Пусть сторона треугольника b равна 10, угол β  = 30º, угол α = 35º. Тогда получим подставив в
формулу следующие значения: Сторона (a) = (10 * sin 35) / sin 30   = 8.71723 мм.