Как найти более основание трапеции

Найти большее основание трапеции. Здравствуйте! В той статье разберём группу задач связанных с площадью трапеции. Часть задачек решается устно, другая часть нет, но всё же быстро. Перед решением стоит посмотреть статью «Углы равнобедренной трапеции», и информацию о выводе формулы площади. Сама формула:

Рассмотрим задачи:

27627. Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.

Площадь трапеции (формула):

Нам известны основания и площадь, можем записать:

Ответ: 8

27628. Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.

Формула площади при данных обозначениях вершин:

Нам известны основание, площадь и высота, можем записать:

Ответ: 7

*Заметьте, что в условии не сказано какое именно дано основание меньшее и большее, да это и не важно для процесса вычисления.

27630. Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.

Формула площади при данных обозначениях вершин:

Нам известны средняя линя и площадь, можем записать:

Ответ: 8

27632. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

Для того, что бы найти периметр нам необходимо найти чему равна боковая сторона. Как известно, у равнобедренной трапеции боковые стороны равны.

Используя данные в условии мы можем вычислить высоту:

Опустим  высоту из точки D к основанию АВ и точку пересечения обозначим как Е:

Теперь мы можем вычислить отрезок AH и по теореме Пифагора в прямоугольном треугольнике ADH найти гипотенузу AD (боковую сторону трапеции):

По теореме Пифагора:

Таким образом периметр будет равен 7+13+5+5 = 30

Ответ: 30

27635. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Для вычисления площади нам необходимо найти высоту. Выполним дополнительные построения:

Нижнее основание будет разбито на отрезки 6, 14 и 6. По теореме Пифагора мы можем вычислить высоту:

Таким образом площадь будет равна:

Ответ: 160

27636. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.

Задача обратная предыдущей. Из данных  в условии мы можем вычислить высоту:

Теперь выполним дополнительные построения (опустим  высоты):

Большее основание разбивается ими на отрезки 3, 7 и 3. По теореме Пифагора можем вычислить боковую сторону:

Ответ: 5

27637. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150⁰. Найдите площадь трапеции.

Для вычисления площади необходимо найти высоту. Это мы можем сделать рассмотрев прямоугольный треугольник АВН:

Высоту нашли, вычисляем площадь:

Ответ: 42

27593. Основания трапеции равны 1 и 3, высота  — 1. Найдите площадь трапеции.

Посмотреть решение

27594. Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.

Посмотреть решение

27629. Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.

Посмотреть решение

27631. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Посмотреть решение

27633. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45⁰.

Посмотреть решение

27634. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.

Посмотреть решение

27638. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

Посмотреть решение

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

P.S: Расскажите о статье и сайте в социальных сетях.

Всего: 71    1–20 | 21–40 | 41–60 | 61–71

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 71    1–20 | 21–40 | 41–60 | 61–71

Все формулы сторон равнобедренной трапеции

1. Формула длины основания равнобедренной трапеции через среднюю линию

a – нижнее основание

b – верхнее основание

m – средняя линия

Формулы длины основания :

2. Формулы длины сторон через высоту и угол при нижнем основании

a – нижнее основание

b – верхнее основание

c – равные боковые стороны

α – угол при основании трапеции

h – высота трапеции

Формулы всех четырех сторон трапеции :

3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями

a – нижнее основание

b – верхнее основание

c – равные боковые стороны

d – диагонали

α , β – углы между диагоналями

h – высота трапеции

Формулы длины сторон трапеции:

справедливо для данной ситуации:

4. Формулы длины сторон равнобедренной трапеции через площадь

a – нижнее основание

b – верхнее основание

c – равные боковые стороны

α , β – углы при основаниях

m – средняя линия

h – средняя линия

Формулы длины сторон равнобедренной трапеции через площадь :

Формулы трапеции

Для расчёта всех основных параметров трапеции воспользуйтесь калькулятором.

Виды трапеции

1. Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
2. Равнобедренная трапеция – это такая трапеция, у которой боковые стороны равны
3. Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне

Свойства трапеции

1. Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме $$ FE = $$
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
   Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD
3. Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
4. Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
6. Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е. $$ KL = $$
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
2. В равнобедренной трапеции длины диагоналей равны (AC = BD)
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная
4. Около равнобедренной трапеции можно описать окружность
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований

Формулы площади произвольной трапеции

Площадь трапеции через основания и высоту

Площадь трапеции через среднюю линию и высоту

Площадь трапеции через диагонали и угол между ними

Площадь трапеции через четыре стороны

Формулы площади равнобедренной трапеции

Площадь трапеции через стороны

Площадь трапеции через стороны и угол

$$ S = AD * sin(∠ADC) * (DC – AD * cos(∠ADC)) $$ $$ S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC)) $$

Площадь трапеции через диагонали и угол между ними

Площадь трапеции через среднюю линию, боковую сторону и угол при основании

$$ S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB) $$

Площадь трапеции если в нее вписана окружность

Формулы сторон произвольной трапеции

Основание через другое основание и среднюю линию

$$ AB = 2 * FE – DC $$ $$ DC = 2 * FE – AB $$

Основание через другое основание, диагонали и угол между ними

$$ DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ AB = DC – AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD) $$ $$ AB = DC – AD * cos(∠ADC) – BC * cos(∠BCD) $$ $$ AD = $$ $$ BC = $$

Формулы сторон равнобедренной трапеции

$$ AD = $$ $$ AD = $$ $$ DC = AB + 2 * AG * ctg(∠ADC) $$ $$ AB = DC – 2 * AG * ctg(∠ADC) $$ $$ DC = AB + 2 * AB * cos(∠ADC) $$ $$ AB = DC – 2 * AB * cos(∠ADC) $$

Длина основания через диагональ, боковую сторону и другое основание

Длина боковой стороны через диагональ и основания

Длина основания через высоту, другое основание, диагонали и угол между ними

Длина основания через высоту, другое основание и площадь трапеции

Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании

Длина боковой стороны через площадь трапеции, основания и угол при основании

Формулы сторон прямоугольной трапеции

$$ DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD) $$ $$ AB = DC – BC * cos(∠BCD) = DC – AD * ctg(∠BCD) $$ $$ DC = AB + sqrt $$ $$ AB = DC – sqrt $$

Длина основания через боковую сторону, другое основание, диагонали и угол между ними

Длина основания через площадь трапеции, другое основание и высоту

Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG) $$ DC = <2 * S over AD>- AB $$ $$ AB = <2 * S over AD>- DC $$

Формулы диагоналей произвольной трапеции

Длина диагоналей через четыре стороны

Длина диагоналей по теореме косинусов

Длина диагоналей через высоту

Длина диагоналей через стороны и другую диагональ

Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей

Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей

Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей

Формулы диагоналей равнобедренной трапеции

Длина диагоналей через стороны

Длина диагоналей по теореме косинусов

Длина диагоналей через высоту основание и угол при основании

Длина диагоналей через сторону и высоту

Формулы диагоналей прямоугольной трапеции

Формулы средней линии произвольной трапеции

Длина средней линии через основания

Длина средней линии через основание, высоту и углы при нижнем основании

Длина средней линии через диагонали, высоту и угол между диагоналями

Длина средней линии через площадь и высоту

Формулы средней линии равнобедренной трапеции

Длина средней линии через основания

Длина средней линии через основание, высоту и углы при нижнем основании

$$ FE = DC – AG * ctg(∠ADC) = AB + AG * ctg(∠ADC) $$

Длина средней линии через основания, боковую сторону и высоту

Длина средней линии через диагонали, высоту и угол между диагоналями

Длина средней линии через площадь и боковую сторону

Формулы средней линии прямоугольной трапеции

Длина средней линии через основания, высоту и угол при нижнем основании

Длина средней линии через основания, боковую сторону и угол при нижнем основании

Длина средней линии через основания и боковые стороны

Длина средней линии через диагонали, высоту и угол между диагоналями

Формулы высоты произвольной трапеции

Длина высоты через четыре стороны

Длина высоты через боковую сторону и прилегающий угол к основанию

$$ AG = AD * sin(∠ADC) = BC * sin(∠BCD) $$

Длина высоты через диагонали и углы между ними

Длина высоты через среднюю линию, диагонали и углы между ними

Длина высоты через площадь и основания

Длина высоты через площадь и среднюю линию

Формулы высоты равнобедренной трапеции

Длина высоты через по сторонам

Длина высоты через боковую сторону и прилегающий угол к основанию

Длина высоты через основания и прилегающий угол к основанию

Длина высоты через диагонали и углы между ними

Длина высоты через площадь и основания

Длина высоты через площадь и среднюю линию

Формулы боковых сторон прямоугольной трапеции

Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.

Сторона BC по трём сторонам

Сторона BC через основания и угол ∠BCD

Сторона BC через Сторону AD

Сторона BC через площадь, среднюю линию и угол ∠BCD

Сторона BC через площадь, основания и угол ∠BCD

Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

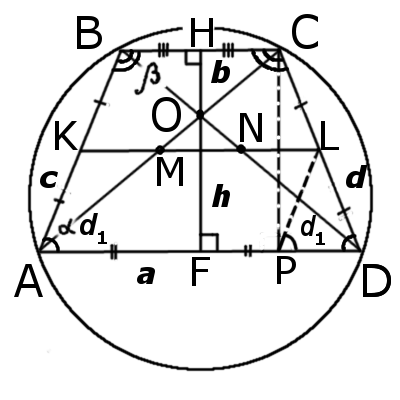Рис.1

Признаки равнобедренной трапеции

∠ABC = ∠BCD и ∠BAD = ∠ADC

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

Основные свойства равнобедренной трапеции

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD

9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

a = b + 2 h ctg α = b + 2 c cos α

b = a – 2 h ctg α = a – 2 c cos α

c =	h	=	a – b
sin α	2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d 1 2 – c 2	b =	d 1 2 – c 2	c = √ d 1 2 – ab
b	a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	– b b =	2S	– a
h	h

4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

m = a – h ctg α = b + h ctg α = a – √ c 2 – h 2 = b + √ c 2 – h 2

2. Формула средней линии трапеции через площадь и сторону:

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

1. Формула высоты через стороны:

h =	1	√ 4 c 2 – ( a – b ) 2
2

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a – b	tg β	= c sin β
2

Диагонали равнобедренной трапеции

Формулы длины диагоналей равнобедренной трапеции:

d ₁ = √ a 2 + c 2 – 2 ac cos α

d ₁ = √ b 2 + c 2 – 2 bc cos β

4. Формула длины диагонали через высоту и основания:

d 1 =	1	√ 4 h 2 + ( a + b ) 2
2

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

1. Формула площади через стороны:

S =	a + b	√ 4 c 2 – ( a – b ) 2
4

2. Формула площади через стороны и угол:

S = ( b + c cos α ) c sin α = ( a – c cos α ) c sin α

3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:

S =	4 r 2	=	4 r 2
sin α	sin β

4. Формула площади через основания и угол между основой и боковой стороной:

5. Формула площади ранобедренной трапеции в которую можно вписать окружность:

S = ( a + b ) · r = √ ab ·c = √ ab ·m

6. Формула площади через диагонали и угол между ними:

S =	d 1 2	· sin γ	=	d 1 2	· sin δ
2	2

7. Формула площади через среднюю линию, боковую сторону и угол при основании:

S = mc sin α = mc sin β

8. Формула площади через основания и высоту:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d 1
4√ p ( p – a )( p – c )( p – d 1)

где

a – большее основание

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

[spoiler title=”источники:”]

http://calc-online24.ru/formula/trapez

http://ru.onlinemschool.com/math/formula/trapezium_isosceles/

[/spoiler]