Версия для печати и копирования в MS Word
1
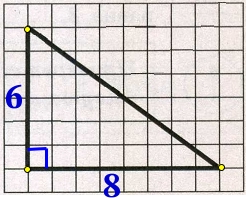
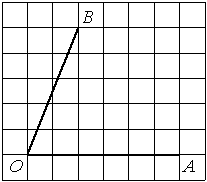
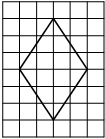
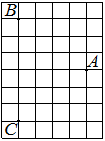
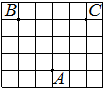
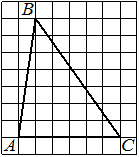
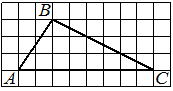
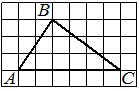
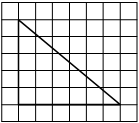
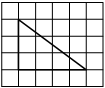
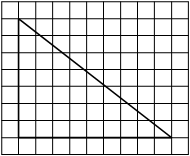
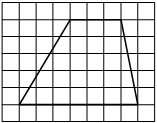
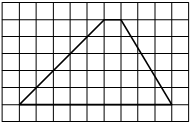
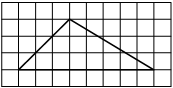
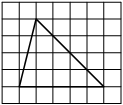
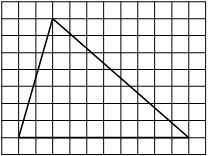
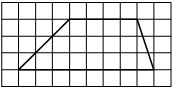
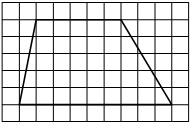
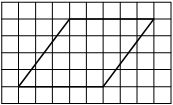
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
2
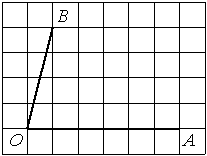
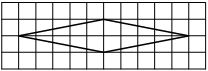
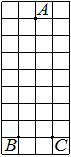
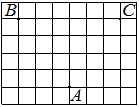
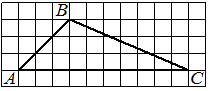
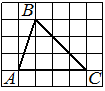
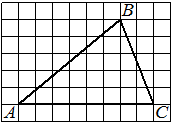
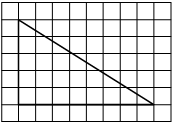
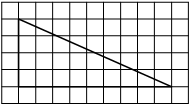
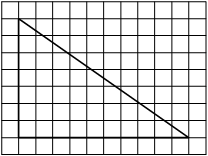
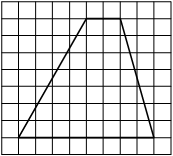
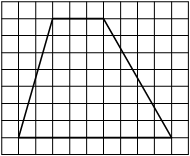
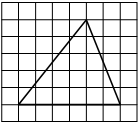
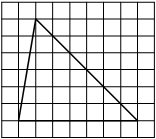
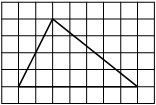
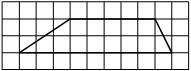
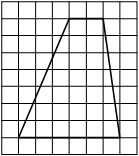
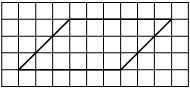
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
3
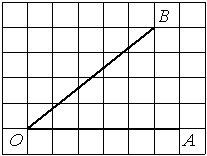
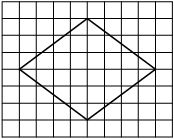
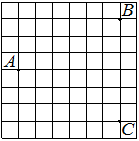
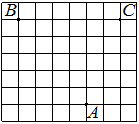
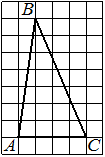
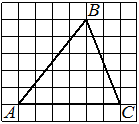
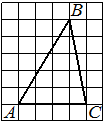
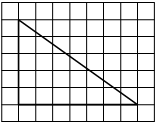
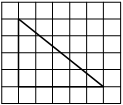
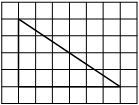
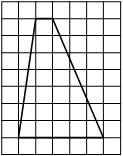
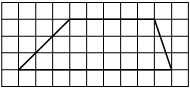
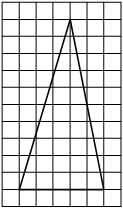
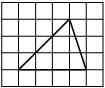
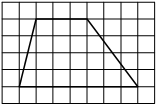
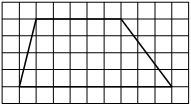
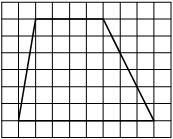
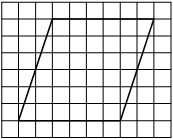
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
4
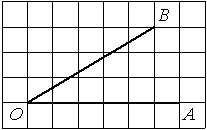
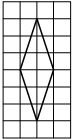
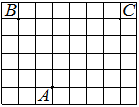
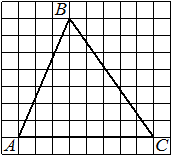
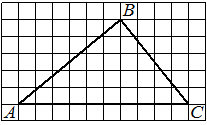
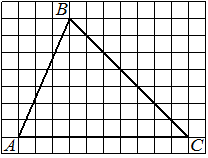
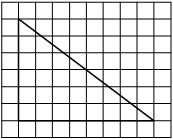
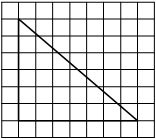
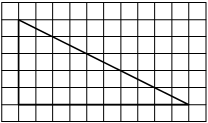
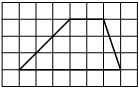
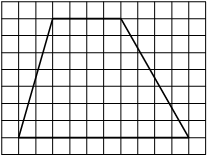
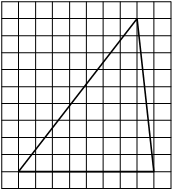
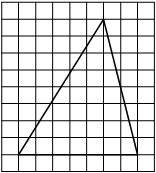
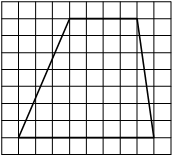
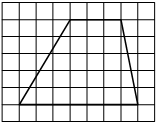
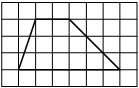
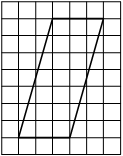
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
5
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
6
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
7
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
8
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
9
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
10
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
11
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
12
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Источник: Банк заданий ФИПИ
13
|
На клетчатой бумаге с размером клетки |
|
14
|
На клетчатой бумаге с размером клетки |
|
15
|
На клетчатой бумаге с размером клетки |
|
16
|
На клетчатой бумаге с размером клетки |
|
17
|
На клетчатой бумаге с размером клетки |
|
18
|
На клетчатой бумаге с размером клетки |
|
19
|
На клетчатой бумаге с размером клетки |
|
20
|
На клетчатой бумаге с размером клетки |
|
21
|
На клетчатой бумаге с размером клетки |
|
22
|
На клетчатой бумаге с размером клетки |
|
23
|
На клетчатой бумаге с размером клетки |
|
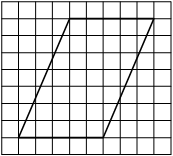
На клетчатой бумаге с размером клетки 1 х 1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Источники: Основная волна ОГЭ 2022, ОГЭ Ященко 2022 (36 вар)
Решение:
Катеты треугольника равны 6 и 8. Больший из них равен 8.
Ответ: 8.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.5 / 5. Количество оценок: 41
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Решение №2201 На клетчатой бумаге с размером клетки 1 х 1 изображён прямоугольный треугольник. Найдите длину его большего катета.
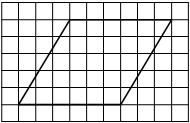
На клетчатой бумаге с размером клетки 1 х 1 изображён прямоугольный треугольник. Найдите длину его большего катета.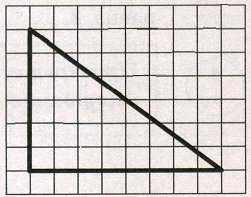
Источник: ОГЭ Ященко 2022 (36 вар)
Катеты треугольника равны 6 и 8. Больший из них равен 8.
Ответ: 8.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Катеты прямоугольного треугольника – свойства, основные формулы и примеры решений
Понятия и определения
Знак треугольника в первом веке ввёл в обиход древнегреческий философ и учёный Герон. Его свойства изучали Платон и Евклид. По их мнению, вся поверхность прямолинейного вида состоит из множеств различных треугольников. В геометрии под ними понимается область, лежащая в плоскости, ограниченной тремя отрезками, соединяющимися в трёх точках, не принадлежащих одной прямой.
Линии, образующие область, называются сторонами, а точки соприкосновения отрезков — вершинами. Основными элементами многоугольника являются:
- Медиана — отрезок, соединяющий середину с противолежащим углом. В треугольнике три медианы, которые пересекаются в одной точке. Называется она центроидом и определяет центр тяжести объекта.
- Высота — линия, опущенная из вершины на противоположную сторону, образующую с ней прямой угол. Место пересечения высот называют ортоцентром.
- Биссектриса — прямая, проведённая из угла таким образом, что делит его на две равные части. Если в треугольник вписать окружность, соприкасающуюся с его сторонами, то её центр совпадёт с точкой пересечения биссектрис. Называют это место — инцентр.
В зависимости от видов углов, треугольники разделяют на остроугольные, тупоугольные и прямоугольные. Но каким бы ни был тип фигуры, существует закономерность, что сумма всех углов всегда равна 180 градусам. Поэтому как минимум два угла должны быть острыми.
Различают треугольники и по числу равных сторон. Так, если они все равны, фигура называется равносторонней. Когда же по величине совпадают только две стороны, то многоугольник является равнобедренным. Его главное свойство в том, что углы равны. Частным случаем равнобедренного многоугольника является правильный треугольник (разносторонний).
Чтобы не возникала путаница, существуют стандартные обозначения величин. Вершины подписываются заглавными буквами A, B, C, а углы – греческими символами: α, β, γ. Стороны же обозначают прописными буквами латинского алфавита: a, b, c.
Свойства прямоугольного треугольника
Прямоугольный треугольник — это симметричный многоугольник, сумма двух углов которого равняется 90 градусов. Так как общая сумма всех трёх углов составляет 180 градусов, то соответственно третий угол равен 90 градусам. Стороны, образующие его, называют катетами, а оставшийся отрезок гипотенузой.
К основным свойствам фигуры относят следующее:
- гипотенуза многоугольника всегда больше любого из его катетов;
- сторона, располагающаяся напротив угла в 30 градусов, составляет половину гипотенузы;
- два катета являются высотами треугольника;
- середина окружности, описанная вокруг фигуры, совпадает с гипотенузой, при этом медиана, опущенная из прямого угла на гипотенузу, одинаковая с радиусом круга;
- численное значение гипотенузы, возведённое в квадрат, равно сумме квадратов катетов (теорема Пифагора).
Эти основные признаки при решении геометрических задач помогают определить класс треугольника и рассчитать его величины. Большое значение при этом имеет вычисление значений катетов.
Так, если известна гипотенуза, то найти катеты, зная угол, не составит труда. Определив же длину катетов, вычислить оставшуюся сторону можно по теореме Пифагора. Периметр фигуры определяют сложением двух катетов и гипотенузы, а площадь находят перемножением катетов и делением полученного ответа на два.
Зная катеты, довольно просто вычислить угол. Нужно всего лишь запомнить, что соотношение сторон между собой равно тангенсу противолежащего угла и котангенсу, находящемуся рядом. При этом, зная любой из углов, найти второй можно простым вычитанием известного значения из девяноста. Высота же у прямоугольника равна косинусу прилежащего угла.
Формула для нахождения биссектрисы и медианы довольно сложная. Для нахождения первой величины используют преобразование радикала из суммы квадратов катетов к двум, а второй – подстановку радикала вместо стороны, лежащей напротив прямого угла.
Теорема Пифагора и углы
Эта теорема занимает одно из центральных мест в математике. Алгебраическая формулировка её гласит, что в прямоугольнике квадрат длины гипотенузы по своему значению равен сумме квадратов двух прилегающих к ней сторон, то есть катетов. Например, если обозначить гипотенузу буквой c, а катеты а и b, то математически её можно записать в виде формулы: a 2 +b 2 = c 2 .
Существует несколько доказательств этой теоремы. Самое простое из них – это использование подобия треугольников. В его основе лежат аксиомы. Пусть имеется геометрическая фигура ABC, у которой вершина C является прямой, то есть её угол равен 90 градусов. Если из точки С опустить высоту, а место пересечения с противолежащей стороной обозначить H, то получится два треугольника. Один будет состоять из вершин AHC, а другой BHC. Эти новые фигуры подобны ABC по двум углам. Следующие выражения будут верными:
Приведённые записи эквивалентны равенствам: BC 2 = AB * HB; AC 2 = AB * AH. Сложив первую и вторую формулу, получается: BC 2 + AC 2 = AB * (HB + AH) = AB 2 . Что и следовало доказать.
Используя это фундаментальное правило и свойство, что катет, расположенный напротив угла в 30 градусов, равен половине гипотенузы, проводят множество расчётов, связанных с вычислением длин сторон. Для доказательства, что AC = BC/2, приводят следующие рассуждения.
Так как вершина B равна 30 градусам, то, согласно правилу, разворот С должен составлять C =30*2 = 60 градусов. К имеющемуся треугольнику можно приложить точно такую же фигуру, делая сторону AB центром симметрии. Тогда для многоугольника BCD будет справедливо, что B = D = 60º. Исходя из этого можно утверждать, что DC = BC. Но, так как AC = ½ DC, то соответственно AC = ½ BC.
Но не всегда известны все данные, необходимые для нахождения длины катета по приведённым теоремам. Поэтому для вычисления катетов используются и тригонометрические соотношения.
Тригонометрические формулы
Для нахождения длины катета прямоугольного треугольника используют простые формулы. Для их применения нужно знать значение любой из сторон и величину разворота произвольной вершины. Существует четыре способа, позволяющих найти катет с использованием тригонометрических правил:
- В основе лежит аксиома, что синус находится из отношения противолежащего катета к гипотенузе. Например, пусть известно что длина гипотенузы составляет 100 сантиметров, а вершина A имеет разворот равный 30 градусам. Используя тригонометрические таблицы, можно утверждать, что синус угла A составляет ½. Учитывая преобразованное выражение, находят катет: a = 100 / 2 =50 (см). Таким образом, синус острого угла численно равен отношению одного из катетов, деленного на гипотенузу: sin A = BC/AB.
- Используется правило, что косинус в прямоугольнике представляет собой отношение прилежащего катета к прямому углу и гипотенузе: cosA = AC/AB. Например, пусть разворот вершины C равен 60 градусам, а гипотенуза равна 100 сантиметрам. Согласно тригонометрической таблице, угол в 60 градусов равен ½. Подставив это значение в формулу, можно найти значение катета: a=cos∠C*a; b=½*100=50 сантиметров.
- Тангенс угла можно вычислить, разделив значение длины противолежащего катета к прилежащему. Математическая формула этого утверждения имеет вид: tg = BC/AC. Катет многоугольника может быть найден как b = tg * a. Например, известно, что у фигуры один из углов равен 45 градусов, а длина гипотенузы составляет 100 сантиметров. Так как тангенс 45 градусов равен единице, то ответом на задачу будет: a = 1*100 = 100 сантиметров.
- Котангенс определяется из соотношения прилежащего катета к противолежащему. Фактически это величина, обратная тангенсу: ctg = AC/BC. Например, пусть разворот угла A составляет 30 градусов, а длина катета, находящегося напротив него, равняется 50 сантиметрам. Котангенс 30 градусов соответствует корню из трёх. Подставив в формулу известные данные, можно вычислить неизвестный катет: b =50√3 сантиметров.
Зная, как выглядят тригонометрические формулы и содержание двух теорем, вычислить значение катета можно будет в большинстве поставленных задач.
Типовые примеры
Для решения задач на нахождение катета не нужно обладать какими-то особенными знаниями. Нужно просто внимательно проанализировать условие. Например, пусть известно, что в прямоугольнике один катет длиннее другого на пять сантиметров. При этом площадь фигуры равняется 84 сантиметрам в квадрате. Необходимо определить длины сторон и периметр.
Так как в условии дана площадь, то при решении необходимо отталкиваться от неё. Известно, что площадь прямоугольного треугольника находится по формуле: S = AC*CB/2. Это выражение является частным случаем общей формулы для нахождения площади любого треугольника, где: AC — это высота, а CB — основание. Если принять, что AC равно X, то, согласно условию, длина CB будет составлять x+5.
Исходя из этого, площадь треугольника будет равна: S = (x*(x+5))/2. Подставив вместо S заданное значение, можно получить квадратное уравнение: x2 + 5x — 84 = 0. Решать его лучше методом детерминанта. Корнями уравнения будут -12 и 7. Так как -12 не удовлетворяет условию задачи, то верным ответом будет семь.
Длина второго катета равняется семи сантиметрам. Первого: AC = 7−5 = 2 см. Зная оба катета, по теореме Пифагора можно найти гипотенузу: c = (22 + 72)½ = (4+49)½ = 531/2 = 7,3 см. Найдя длины всех сторон, можно без усилий найти периметр обыкновенным сложением: P = 2+7+7,3 = 16,3 см. Задача решена.
Довольно интересные, но в то же время простые задачи на нахождение сторон и углов при известной длине гипотенузы и значения разворота одной из вершин. Пусть имеется прямоугольный треугольник, у которого гипотенуза BC равняется пяти сантиметрам, а угол между ней и катетом составляет 60 градусов. Нужно определить все остальные стороны и углы.
Так как известна гипотенуза и острый угол, то, воспользовавшись тригонометрическими формулами, можно найти длины катетов: AC=BC*sin60 = 5*(3) ½ /2; AB=BC*cos60 = 5/2. Сумма всех углов в треугольнике равна 180 градусов, так как один из них прямой, а второй задан и составляет 60 градусов, то третий находится путём вычитания C = 180 – (90 + 60) = 30.
Как найти катет прямоугольного треугольника
С задачками по геометрии сталкиваются все в средней школе. Кому-то такие задачки даются сложно, а кто-то их щелкает, как орешки. На самом деле эти задачи не особо сложные, просто нужно вникнуть и понять определенный алгоритм решения. Давайте подробнее разберем, как найти катет прямоугольного треугольника.
Геометрические определения
- Если у треугольника есть прямой угол (∠=90 о ), то он является прямоугольным.
- Катет – линия, создающая угол 90 градусов в треугольнике.
- Гипотенуза – линия, которая находится напротив угла равного 90 градусов.
- Две ортогональные линии образуют прямой угол, величина которого 90 градусов. Еще можно сказать, что это половина развернутого угла.
Свойства сторон в прямоугольном треугольнике
Гипотенуза всегда больше каждого из катетов.
Сторона, которая находится напротив угла равного 30 градусов, равна половине величины гипотенузы.
К прямоугольному треугольнику можно применить теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Формулы для решения задач
- Если мы знаем величину одного катета А и гипотенузы С, то второй катет B мы вычислим при помощи теоремы Пифагора.
- Угол А мы может определись с помощью формулы синуса:
- Так как сумма всех углов геометрической фигуры всегда равна 180 градусов, то другой острый угол можно вычислить по формуле:
Примеры решения задач
Задача №1:
В треугольнике АВС с ∠А=90 градусов, ∠С=60 градусов и катетом АВ=5 см. Найти длину катета АС.
В прямоугольном треугольнике АВС найдем угол В:
∠В=90 о — ∠С=90 о — 60 о = 30 о
Поскольку ∠В=30 о , то катет АВ равен половине гипотенузы ВС, а значит,
Длину катета АС найдем с помощью теоремы Пифагора:
Задача №2:
В равнобедренном и прямоугольном треугольнике АВС гипотенуза больше катета на 2 см. Найти длину сторон треугольника.
В треугольной фигуре АВС обозначим катеты АВ=АС=х, тогда ВС=2+х. Запишем теорему Пифагора для данного треугольника:
ВС 2 = АВ 2 + АС 2 => (х+2) 2 = х 2 + х 2 или х 2 – 4х – 4 = 0
Решая это уравнение и учитывая условия задачи, получим
т.е. АВ = АС = (2+2) см, ВС = (4+2) см
Ответ: АВ = АС = (2+2) см, ВС = (4+2) см
Как видите, процесс решения геометрических задач по нахождению катета в прямоугольном треугольнике не особо сложный. Нужно просто приложить усилия, посидеть и вникнуть в суть задачи. Когда начнете писать формулы, решение придет к вам само. Удачи в решении задачек по геометрии, теперь вы знаете, как найти катет прямоугольного треугольника.
[spoiler title=”источники:”]
http://nauka.club/matematika/katet-v-pryamougolnom-treugolnike.html
http://dobriy-sovet.ru/kak-najti-katet-pryamougolnogo-treugolnika/
[/spoiler]
Это задание из ОГЭ по математике предлагает найти площади, углы, длины геометрических фигур, нарисованных на фоне в клетку. Задание 18 с кратким ответом, в ответ идет только число.
Реальные задания №18 по геометрии из банка ФИПИ
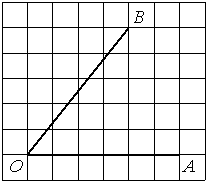
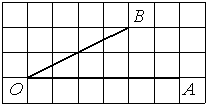
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=6/2=3.
Ответ: 3
AE8B22
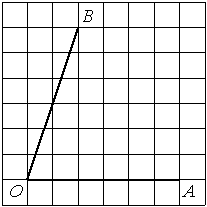
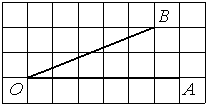
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=6/4=1,5.
Ответ: 1,5
09C3B1
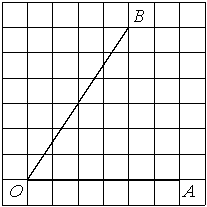
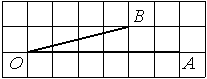
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=5/4=1,25.
Ответ: 1,25
739060
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=5/2=2,5.
Ответ: 2,5
0747AA
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=4/1=4.
Ответ: 4
9C09A9
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=4/5=0,8.
Ответ: 0,8
A1ECAA
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
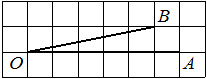
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=3/5=0,6.
Ответ: 0,6
887E42
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=2/4=0,5.
Ответ: 0,5
201054
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=2/5=0,4.
Ответ: 0,4
E73651
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=1/5=0,2.
Ответ: 0,2
A601D0
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=1/4=0,25.
Ответ: 0,25
51BEC9
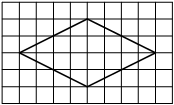
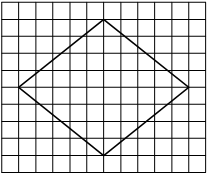
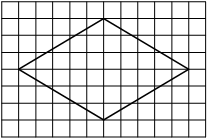
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 6*4=12
Ответ: 12
F519DD
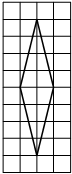
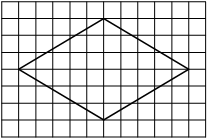
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10*2=10
Ответ: 10
704DB1
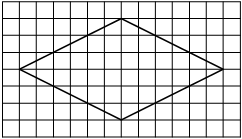
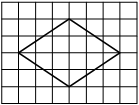
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 6*8=24
Ответ: 24
2F4DA5
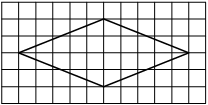
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 6*2=6
Ответ: 6
1F239C
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 8 * 4 = 16
Ответ: 16
33E327
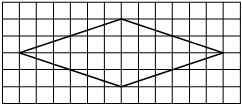
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 6 = 36
Ответ: 36
0B92D0
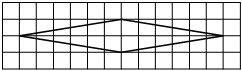
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 8 * 2 = 8
Ответ: 8
3B5D8B
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 4 = 20
Ответ: 20
CFCA33
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 8 = 40
Ответ: 40
3B008A
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 6 = 30
Ответ: 30
8372E0
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 4 = 24
Ответ: 24
FFD1EE
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 2 = 12
Ответ: 12
E2A932
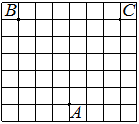
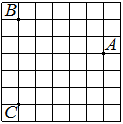
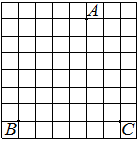
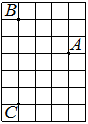
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 3
969F4E
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 5
AFB9A1
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 1
D234F7
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 2
68F679
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 4
9672D7
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 5
3F311F
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 6
C598DA
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 8
FCC29D
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 7
0DBF9B
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 6
B73FA9
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 1
78BDFE
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 7
CB1715
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 3
107F53
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 2
5B4C37
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4
FEDC09
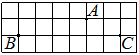
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 6
C563EA
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 5
B2853A
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4
FE13B1
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 2
C8BF73
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 5
A4B62F
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 2
DA3762
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 7
C576A6
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 1
9D880E
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4
078B48
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 6
854014
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 3
B4DCCF
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 8
259D23
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3
9C2804
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5
BC4EBE
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2
7ECBCE
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4
D2D94B
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4
8F5C52
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2
686EFB
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3
07C968
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5
E3456A
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3
794271
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4
A1906B
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2
E52B99
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5
E331C7
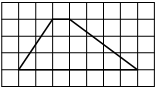
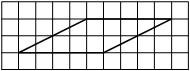
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 6
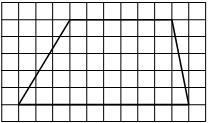
F7FF65
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 8
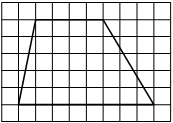
AAC1BC
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 7
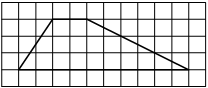
2BD44A
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 8
6DE9A6
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 4
39A91A
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 9
197283
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 5
2EA9C2
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 7
ED1F0E
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 9
10323E
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 10
ED4E1A
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 6
4FAEEC
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 10
F8232E
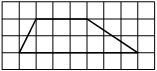
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (1+7) : 2 = 4
Ответ: 4
351A72
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (6+10) : 2 = 8
Ответ: 8
5EFE19
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (4+8) : 2 = 6
Ответ: 6
C05266
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (2+10) : 2 = 6
Ответ: 6
CFD6D8
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (3+7) : 2 = 5
Ответ: 5
3BD771
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (2+8) : 2 = 5
Ответ: 5
869450
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (1+5) : 2 = 3
Ответ: 3
19D522
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (2+6) : 2 = 4
Ответ: 4
A28F9D
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (1+9) : 2 = 5
Ответ: 5
2EF821
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (3+9) : 2 = 6
Ответ: 6
45A5FF
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (5+9) : 2 = 7
Ответ: 7
7AAADC
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (4+10) : 2 = 7
Ответ: 7
321F00
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
87C214
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 6
6CB64A
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8
4801B0
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12
DEA70E
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8
6D0D8F
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12
8D9098
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8
90A16B
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
F3D7EA
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
35106F
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
1C594B
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 6
E4F439
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12
657F97
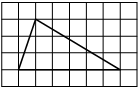
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 6 * 3 = 9
Ответ: 9
E873D3
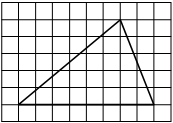
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 5 = 20
Ответ: 20
9E69AF
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 3 = 12
Ответ: 12
53C928
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 6 * 5 = 15
Ответ: 15
EE2C25
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 5 * 10 = 25
Ответ: 25
1B4EAF
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 9 = 36
Ответ: 36
94B40E
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 5 * 4 = 10
Ответ: 10
F50FF8
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 6 = 21
Ответ: 21
3A7F81
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 4 * 3 = 6
Ответ: 6
DFB4EA
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 8 = 28
Ответ: 28
7AEBD7
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 10 * 7 = 35
Ответ: 35
4718F7
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 2 = 14
Ответ: 14
0C5645
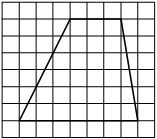
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (7+3) * 4= 20
Ответ: 20
695D77
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 7= 42
Ответ: 42
07B1AD
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 3 = 18
Ответ: 18
4774FE
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 2= 14
Ответ: 14
284762
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 4= 28
Ответ: 28
2916B2
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 5= 25
Ответ: 25
867701
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 5= 35
Ответ: 35
B5D99F
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (2+6) * 7= 28
Ответ: 28
B11571
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 6= 36
Ответ: 36
E46263
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (2+6) * 3= 12
Ответ: 12
283DE4
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 2= 10
Ответ: 10
383C46
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 6= 30
Ответ: 30
2E7B84
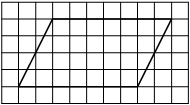
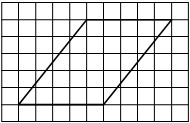
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 4 = 28
Ответ: 28
71E23E
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 2 = 10
Ответ: 10
3BD9B6
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 4 = 20
Ответ: 20
5C5046
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 3 = 18
Ответ: 18
566A4E
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 6 = 36
Ответ: 36
0275CC
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 3 * 7 = 21
Ответ: 21
E81F8D
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 7 = 35
Ответ: 35
2A59D7
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 2 = 14
Ответ: 14
5FC71A
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 5 = 30
Ответ: 30
257B6F
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 6 = 42
Ответ: 42
839354
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 4 * 3 = 12
Ответ: 12
C1A1AF
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 5 = 25
Ответ: 25
9B4AE0
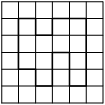
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 14
11403B
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 8
CDF457
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 15
06B968
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 10
AFB70E
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 13
C4025D
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 16
E4CBB2
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 9
211628
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 17
5D3FCF
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 19
320729
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 18
C72856
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 12
BB2950
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 11
F78C61
Опубликовано 3 года назад по предмету
Математика
от аня3129
-
Ответ
Ответ дан
bashirbatyrovСосчитай клеточки большего катета-это и будет его длина,т.е 10
-
Ответ
Ответ дан
ИльяСтеРус55Больший катет равен 10 клеткам (если 2 клетки= 1 см, то больший катет равен 5 см)
Самые новые вопросы
Математика – 3 года назад
Решите уравнения:
а) 15 4 ∕19 + x + 3 17∕19 = 21 2∕19;
б) 6,7x – 5,21 = 9,54
Информатика – 3 года назад
Помогите решить задачи на паскаль.1)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти произведение всех элементов массива.2)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти сумму четных элементов массива.3)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива.4)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива среди элементов,
кратных 3.
География – 3 года назад
Почему япония – лидер по выплавке стали?
Математика – 3 года назад
Чему равно: 1*(умножить)х? 0*х?
Русский язык – 3 года назад
В каком из предложений пропущена одна (только одна!) запятая?1.она снова умолкла, точно некий внутренний голос приказал ей замолчать и посмотрела в зал. 2.и он понял: вот что неожиданно пришло к нему, и теперь останется с ним, и уже никогда его не покинет. 3.и оба мы немножко удовлетворим свое любопытство.4.впрочем, он и сам только еле передвигал ноги, а тело его совсем застыло и было холодное, как камень. 5.по небу потянулись облака, и луна померкла.
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.