Чтобы узнать наибольшую из этих десятичных дробей, нужно вначале найти дробь с наибольшей целой частью: у дробей 9,8 и 9,4 целые части – 9, у дробей 10,14 и 10,3 целые части – 10. Целая часть 10 больше целой части 9, значит дроби 9,8 и 9,4 можем больше не сравнивать – они в любом случае будут меньше двух оставшихся(10,14 и 10,3).
Теперь у нас осталось две дроби – 10,14 и 10,3. Целые части у них одинаковые, значит теперь нам нужно сравнивать дробные части. Начнём сравнение с десятых частей (10, 1 и 10, 3). У дроби 10,14 десятичная часть – 1, у дроби 10,3 десятичная часть – 3. Десятичная часть 1 в любом случае будет меньше десятичной части 3, значит можно даже не смотреть на сотую часть первой дроби(,14). Также есть способ полегче: 10,3 = 10,30(к концам десятичных дробей можно прибавлять сколько угодно нолей, они все равно не изменятся). Теперь у нас есть дроби 10,14 и 10,30. Как уже можно понять, сотая часть 14 меньше сотой части 30, а это значит, что десятичная дробь 10,14 меньше десятичной дроби 10,3.
Итак, можно составить тройное неравенство: 9,4 < 9,8 < 10,14 < 10,3. Из этого неравенства, да и из самих вычислений можно легко понять, что десятичная дробь 10,3 является наибольшей в данном списке.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


на главную
Сравнение десятичных дробей
Поддержать сайт![]()
Запомните!
![]()
Удобно сравнивать десятичные дроби с одинаковым количеством цифр (знаков) справа от запятой.
Чтобы сравнить десятичные дроби нужно:
- Убедиться, что у обеих десятичных дробей
одинаковое количество знаков (цифр) справа от запятой. Если нет, то дописываем (убираем) нужное количество
нулей в одной из десятичных дробей. - Сравниваем десятичные дроби слева направо.
Целую часть с целой, десятые с десятыми, сотые с сотыми и т.д. - Когда одна из частей десятичной дроби (целая часть, десятые, сотые и т.д.) окажется больше чем в другой дроби, эта дробь и больше.
Как сравнивать десятичные дроби
Пример. Сравним десятичные дроби:
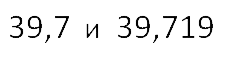
- Сперва дописываем в первой десятичной дроби нужное количество нулей,
чтобы уравнять количество знаков справа от запятой.39,700 и 39,719
- Начинаем сравнивать десятичные дроби слева направо.
Целую часть с целой частью:
39 = 39
Целые части
равны. Переходим к десятым.Десятые с десятыми:
7 = 7
Десятые также равны. Переходим к сотым.
Сотые с сотыми:
0 < 1
Так как сотые второй десятичной дроби оказались больше,
значит и сама дробь больше.39,700 < 39,719
39,7 < 39,719
Другой способ сравнения десятичных дробей
Так же как и в предыдущем методе сравнения
необходимо вначале уравнять количество знаков
справа от запятой в обеих десятичных дробях.
Затем, отбросив запятую в обеих дробях, сравнить
полученные результаты.
Пример:
3,656 и 3,48
Уравняем количество знаков справа у десятичных дробей.
3,656 и 3,480
Теперь отбросим запятые и сравним полученные числа.
3 656 > 3 480
3,656 > 3,48
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
4 мая 2023 в 17:15
Василина Перикова

Профиль
Благодарили: 0
Сообщений: 1

Василина Перикова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
Сравнение десятичных дробей
- Калькулятор сравнения десятичных дробей
Десятичные дроби сравнивают по тем же правилам, что и натуральные числа:
- Из двух десятичных дробей больше та, у которой больше разрядов в целой части. Например:
647,78 > 43,952,
потому что число 647 имеет больше разрядов в целой части, чем число 43.
- Из двух десятичных дробей с одинаковым числом разрядов больше та, у которой больше первая (слева направо) из неодинаковых цифр. Например:
432,35 > 432,21,
потому что у первого числа, цифра в разряде десятых больше, чем цифра в этом же разряде у второго числа.
- Две десятичные дроби равны, если у них одинаковое число разрядов и цифры одинаковых разрядов равны. Например, числа 7832,0954 и 7832,0954 равны. В этом легко убедиться, записав их одно под другим:
7832,0954
7832,0954
Калькулятор сравнения десятичных дробей
Данный калькулятор поможет вам сравнить десятичные дроби. Просто введите две десятичные дроби и нажмите кнопку Сравнить
. Вместо запятой, в записи десятичной дроби, используйте точку:
Содержание
- Сравнение десятичных дробей
- Понятие десятичной дроби
- Свойства десятичных дробей
- Правило сравнения десятичных дробей
- Десятичные дроби
- Понятие десятичной дроби
- Свойства десятичных дробей
- Как записать десятичную дробь
- Как читать десятичную дробь
- Преобразование десятичных дробей
- Как перевести десятичную дробь в проценты
- Преобразование десятичных дробей
- Как перевести десятичную дробь в обыкновенную
- Действия с десятичными дробями
- Как разделить десятичную дробь на натуральное число
- Как разделить десятичную дробь на обыкновенную
- Как умножить десятичную дробь на обыкновенную
Сравнение десятичных дробей

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем мы расскажем, как сравнивать десятичные дроби, вспомним основные определения, виды дробей и разницу между ними.
Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
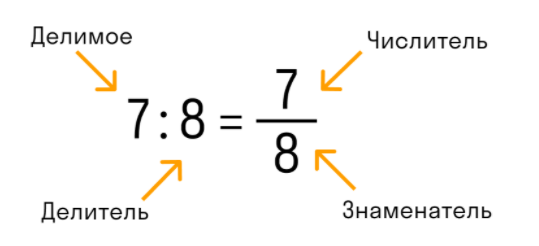
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,1
- 2,53
- 9,932
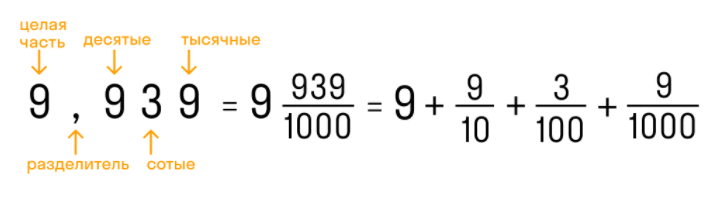
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
Основные свойства
- Дробь не имеет значения, при условии, если делитель равен нулю.
- Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
- Две дроби a/b и c/d называются равными, если a * d = b * c.
- Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Правило сравнения десятичных дробей
Чтобы сравнить две десятичные дроби, сначала нужно сравнить их целые части. Если целые части равны, продолжаем искать первый несовпадающий разряд. Большей будет та дробь, у которой соответствующий разряд больше.
Вот так с первой строчки раскрыли тему сравнения десятичных дробей 😜 Но это еще не все — едем дальше.
Алгоритм сравнения десятичных дробей
- Убедиться, что у обеих десятичных дробей одинаковое количество знаков (цифр) справа от запятой. Если нет, то дописать (убрать) нужное количество нулей в одной из десятичных дробей.
- Сравнить десятичные дроби слева направо. Целую часть с целой, десятые с десятыми, сотые с сотыми и т. д.
- Когда одна из частей десятичной дроби окажется больше, чем другая, эту дробь можно назвать большей.
Применим правило на практике. Сравним десятичные дроби: 15,7 и 15,719.
- Допишем в первой десятичной дроби нужное количество нулей, чтобы уравнять количество знаков справа от запятой: 15,700 и 15,719.
- Сравним десятичные дроби слева направо.
Целую часть с целой частью: 15 = 15. Целые части равны.
Десятые с десятыми: 7 = 7. Десятые также равны.
Сотые с сотыми: 0
Чтобы сравнить две десятичные дроби, нужно уравнять количество знаков после запятой (приписать к одной из них справа нули), затем отбросить запятую, и сравнить два натуральных числа.
Сравним 3,656 и 3,48.
- Уравниваем количество знаков справа после запятой: 3,656 и 3,480.
- Отбросим запятые: 3656 и 3480.
- Сравним полученные числа: 3656 > 3480.
Источник
Десятичные дроби

О чем эта статья:
5 класс, 6 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
| Основные свойства |
|---|
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
- Знаменатель равен 10 — это один ноль.
- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Пример 2. Перевести 37/1000 в десятичную дробь.
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Пример 2. Перевести 4,005 в смешанное число.
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
- Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
- Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
- Разделить целую часть десятичной дроби на это число.
- Поставить запятую в частном и продолжить вычисление, как при обычном делении.
Пример 1. Разделить 4,8 на 2.
- Записать деление уголком.
- Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
- Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
- Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:
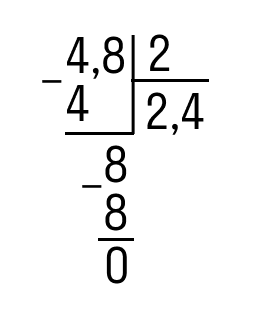
Ответ: 4,8 : 2 = 2,4.
Пример 2. Разделить 183,06 на 45.
- Записать деление уголком.
- Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
- Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
- Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
- Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
- Разделить дробь по правилам:
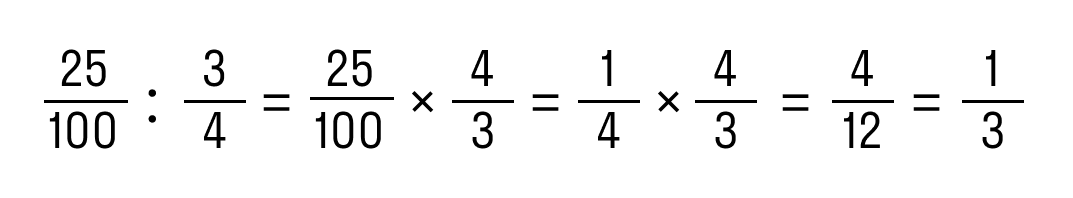
Ответ: 0,25 : 3/4 = 1/3.
Пример 2. Разделить 2,55 на 1 1/3.
- Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
- Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
- Разделить дробь по правилам:
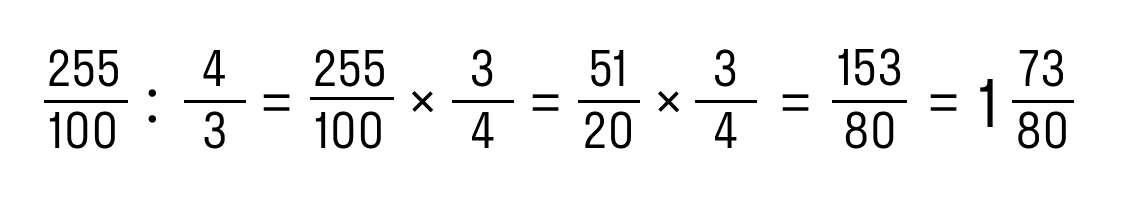
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
- Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
- Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.
Ответ: 2/5 ∗ 0,8 = 0,32.
Пример 2. Умножить 0,28 на 6 1/4.
- Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
- Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Источник
