Шестиугольник представляет собой геометрическую фигуру, многоугольник, который имеет шесть углов и
шесть сторон.
Также существует правильный шестиугольник. Он обладает следующим свойством: все ребра и углы равны.
Каждый угол составляет 120 градусов. А также он состоит из шести правильных и равных
треугольников.
- Длинная диагональ правильного шестиугольника через
площадь - Котроткая диагональ правильного шестиугольника через
площадь - Длинная диагональ правильного шестиугольника через
сторону - Короткая диагональ правильного шестиугольника через
сторону
Длинная диагональ через площадь
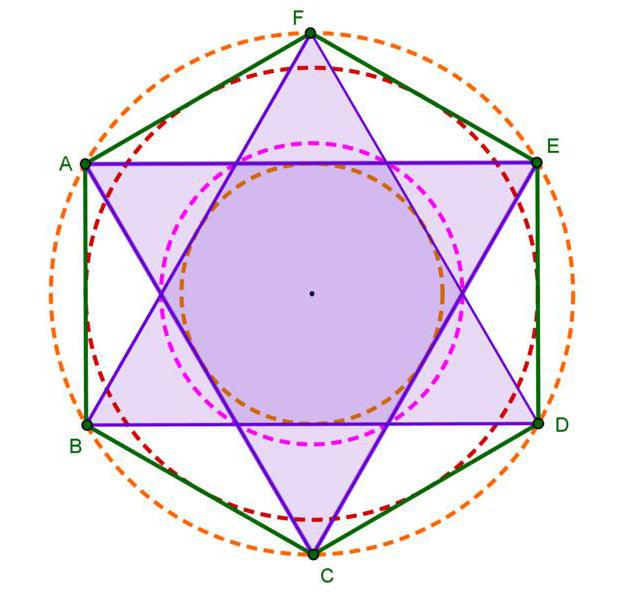
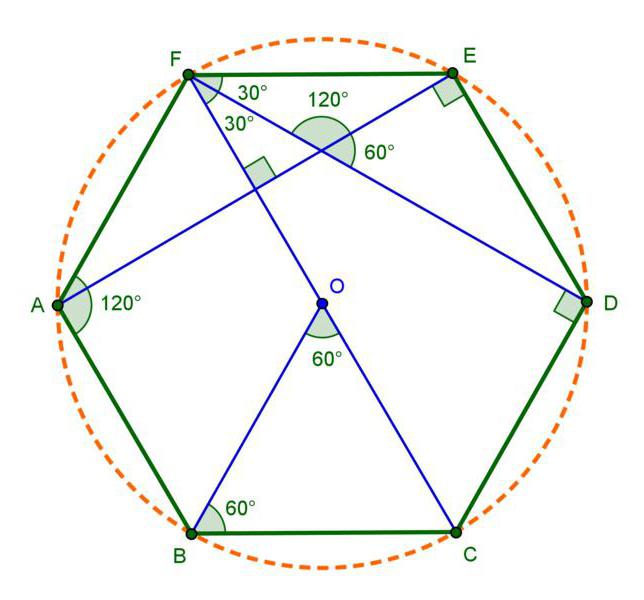
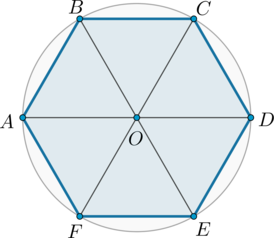
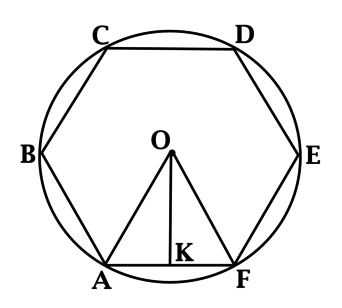
Длинной диагональю на рисунке являются отрезки ВЕ, AD и CF. Все диагонали будут равны между собой.
Это свойство касается как правильной фигуры, так и неправильной. Для нахождения длинной диагонали
правильного шестиугольника понадобится площадь полной фигуры (правильного шестиугольника), которую
можно найти по формуле S = (a * a * √3 * 6) / 4. А диагональ находится по
следующим образом:
D = √((S / 3√3) * 8)
где S — площадь правильного шестиугольника.
Цифр после
запятой:
Результат в:
Пример. Сторона шестиугольника равна 6 см. Тогда площадь: S = (6 * 6 * √3 * 6) / 4 = 54√3 см. D = √((54√3 / 3√3) * 8) = 12 см.
Короткая диагональ через площадь
Короткими диагоналями можно назвать BD, BF, AE или же DF. Для нахождения неизвестной стороны также,
как и в прошлой ситуации, понадобится площадь фигуры, которую возможно найти по следующей формуле:
S = (a * a * √3 * 6) / 4. После этого найденная величина подставляется в
готовую формулу:
D = √((S / √3) * 2)
где S — площадь правильного многоугольника.
Цифр после
запятой:
Результат в:
Пример. Как и в прошлой задаче, ребро равно 6 см. Тогда площадь правильного
шестиугольника = 54√3 см. Далее можно находить и искомую диагональ: D = √((54√3 / √3) * 2) = 6√3
Длинная диагональ через сторону
Длинной диагональю на рисунке являются отрезки ВЕ, AD и CF. Длинную диагональ правильно
шестиугольника можно вычислить и без нахождения площади. Для выполнения математических действий и
нахождения неизвестной переменной надо знать лишь ребро многоугольника:
D = 2a
где a — сторона правильного шестиугольника.
Цифр после
запятой:
Результат в:
Длинная диагональ состоит из двух сторон треугольников, прилегающих друг к другу, поэтому сторону
умножаем на 2.
Пример. В задаче дан правильный шестиугольник. Его ребро равно 3 см. Тогда длинная
диагональ равна 6 см.
Короткая диагональ через сторону
Также существует и другой способ нахождения короткой диагонали, равностороннего шестиугольника.
Например, диагонали BD. Для нахождения достаточно лишь знание стороны фигуры:
D = √(3 * a * a)
где a — сторона правильного шестиугольника.
Цифр после
запятой:
Результат в:
Пример. Сторона АВ равна 10 см. Тогда BD = D = √(3 * 10 * 10) = 10√3 см = 17 см.
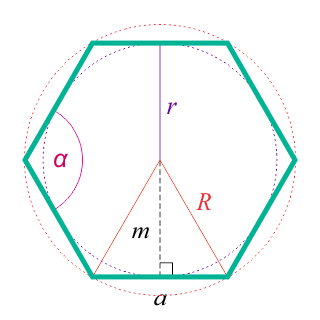
Для более простого понимания такой темы, как вычисление диагонали правильного шестиугольника, стоит
для начала увидеть, что данный многоугольник состоит из шести равносторонних и равных между собой
треугольников. (Неправильный шестиугольник условно можно разделить на шесть равнобедренных
треугольник). О – это центр правильного шестиугольника. Он делит диагонали на равные отрезки. Также
точка пересечения длинных диагоналей является центром вписанной и описанных окружностей. Все
диагонали также равны между собой и делят углы на две равные части, то есть выполняют функцию
биссектрисы, а также высоты или медианы, так как были проведены в равнобедренном треугольнике. Таким
образом будет легче находить какие-то неизвестные отрезки.
Однако существует и более сложный метод – через нахождение площади фигуры. Данную формулу запомнить
просто: S = (a * a * √3) / 4 – она необходима, чтобы вычислить площадь
равностороннего треугольника, где величина а является стороной. А вышеупомянутая фигура состоит из
шести таких геометрических фигур, поэтому конечная формула будет выглядеть так: S = (a * a * √3 * 6) / 4
Таким образом, шестиугольник является не такой уж и сложной фигурой, как кажется на первый взгляд.
Достаточно изучить элементарные свойства и запомнить их.
как найти диагонали в правильном шестиугольники? как найти диагонали в правильном шестиугольники?
Ученик
(229),
закрыт
11 лет назад
Владимир
Мастер
(1589)
11 лет назад
Диагональ правильного шестиугольника в два раза больше его стороны.
Диагональ правильного шестиугольника равна диаметру описанной вокруг него окружности.
Диагональ правильного шестиугольника равна диаметру вписанной в него окружности, поделенному на косинус угла 30 градусов.
Ксения Репина
Ученик
(172)
11 лет назад
Диагональ любого многоугольника – это отрезок, соединяющий две не соседние вершины!
В шестиугольнике они могут быть разной длины, могут равняться радиусу описанной окружности, а могут быть и меньше.
Правильным шестиугольником называется шестиугольник, у которого все стороны и углы равны. Правильный шестиугольник обладает следующими свойствами.
– Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
– Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.
– Меньшая диагональ правильного шестиугольника в раз больше его стороны.
– Угол между сторонами правильного шестиугольника равен 120°.
– Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.
– Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник – это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник – это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник – это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 – 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt <3>) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
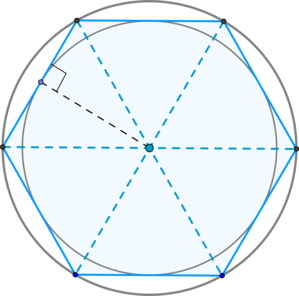
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .
Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :
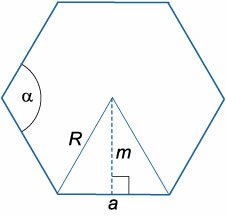
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac<<sqrt 3 >><2>
ormalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac<<3sqrt 3 >><2>
ormalsize),
где (p) − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Правильным шестиугольником называется выпуклый многоугольник с шестью одинаковыми сторонами и шестью углами.
Внутренние углы в правильном шестиугольнике равны (120^circ):
(alpha = 120^circ)
Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
(m = alargefrac >
ormalsize)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac >
ormalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
(R = a)
Периметр правильного шестиугольника
(P = 6a)
Площадь правильного шестиугольника
(S = pr = largefrac >
ormalsize),
где (p) − полупериметр шестиугольника.
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3 ) 2 = 37,68 (см 2 ).
Осталось сосчитать объем: V = 37, 68 * 4 = 150,72 (см 3 ).
Ответ. V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Правильный многоугольник
Правильный многоугольник — это многоугольник, все стороны и углы которого равны.
Вокруг правильного многоугольника можно описать окружность и в него можно вписать окружность. Центры этих окружностей совпадают.
Правильный шестиугольник
Правильный шестиугольник – это шестиугольник, все стороны и углы которого равны.
Описанный многоугольник
Если все стороны многоугольника касаются некоторой окружности , то он называется описанным многоугольником .
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Правильный шестиугольник
Правильный шестиугольник – выпуклый шестиугольник, у которого все углы равны и все стороны равны.
(blacktriangleright) Каждый угол правильного шестиугольника равен (120^circ).
(blacktriangleright) Около правильного шестиугольника можно описать окружность: ее радиус равен его стороне.
(blacktriangleright) Большие диагонали правильного шестиугольника делят его на (6) равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности.
(blacktriangleright) Центры вписанной и описанной около правильного шестиугольника окружностей есть точка пересечения больших диагоналей этого шестиугольника.
(blacktriangleright) Площадь правильного шестиугольника со стороной (a) равна [S=dfrac{3sqrt3}2a^2]
Задание
1
#2430
Уровень задания: Равен ЕГЭ
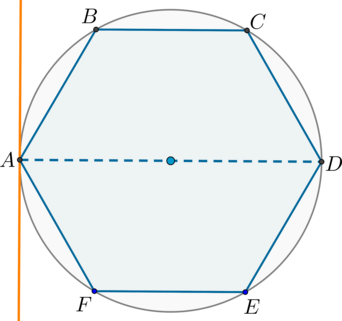
К окружности, описанной около правильного шестиугольника (ABCDEF), в точке (A) проведена касательная. Найдите угол между этой касательной и прямой (AD). Ответ дайте в градусах.
Т.к. центр описанной около правильного шестиугольника окружности есть точка пересечения больших диагоналей, то он лежит на отрезке (AD), то есть (AD) – диаметр описанной окружности. Т.к. радиус, проведенный в точку касания, перпендикулярен касательной, то угол между касательной и (AD) равен (90^circ).
Ответ: 90
Задание
2
#2427
Уровень задания: Равен ЕГЭ
Радиус вписанной в правильный шестиугольник окружности равен (sqrt{12}). Найдите радиус описанной около этого шестиугольника окружности.
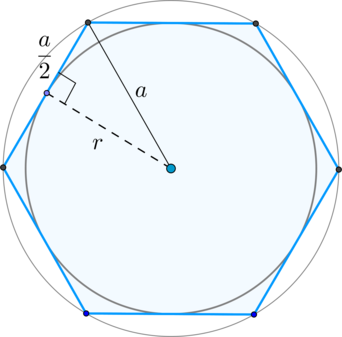
По свойству правильного шестиугольника радиус (r) вписанной окружности равен перпендикуляру, проведенному из центра правильного шестиугольника (центр вписанной и описанной окружности) к стороне шестиугольника; причем этот перпендикуляр падает в середину стороны.
Также по свойству правильного шестиугольника радиус описанной окружности равен его стороне (a). Тогда из прямоугольного треугольника:
[a^2=left(frac a2right)^2+r^2 quad Rightarrow quad a=dfrac 2{sqrt3},r quadRightarrow
quad a=dfrac2{sqrt3}cdot sqrt{12}=4]
Таким образом, и радиус описанной окружности равен (4).
Ответ: 4
Задание
3
#3589
Уровень задания: Равен ЕГЭ
Периметр правильного шестиугольника равен (72). Найдите диаметр описанной окружности.
Если провести все большие диагонали правильного шестиугольника, то они пересекутся в одной точке, которая и будет центром описанной около него окружности (свойство правильного шестиугольника). Рассмотрим чертеж:
Так как угол правильного шестиугольника равен (180^circ(6-2):6=120^circ), а большие диагонали являются биссектрисами углов, то, например, (angle BAO=angle ABO=60^circ), следовательно, (triangle ABO) – равносторонний. То есть радиус окружности равен (AO) и равен (AB). Так как периметр шестиугольника равен (72), то его сторона равна (72:6=12). Тогда диаметр описанной окружности равен (2cdot 12=24).
Ответ: 24
Задание
4
#3588
Уровень задания: Равен ЕГЭ
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной (sqrt3).
Для любого многоугольника, в который можно вписать окружность, верно (S=pcdot r), где (p) – полупериметр, а (r) – радиус вписанной окружности.
Площадь правильного шестиугольника со стороной (a) равна (S=dfrac{3sqrt3}2a^2), полупериметр равен (3a), тогда [dfrac{3sqrt3}2cdot (sqrt3)^2=3sqrt3cdot rquadRightarrowquad
r=1,5]
Ответ: 1,5
Задание
5
#3587
Уровень задания: Равен ЕГЭ
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен (sqrt3).
Для любого многоугольника, в который можно вписать окружность, верно (S=pcdot r), где (p) – полупериметр, а (r) – радиус вписанной окружности.
Площадь правильного шестиугольника со стороной (a) равна (S=dfrac{3sqrt3}2a^2), полупериметр равен (3a), тогда [dfrac{3sqrt3}2a^2=3acdot sqrt3quadRightarrowquad a=2]
Ответ: 2
Задание
6
#2429
Уровень задания: Равен ЕГЭ
Площадь правильного шестиугольника равна (24sqrt3). Найдите длину его большей диагонали.
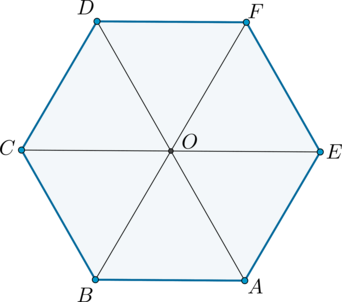
По свойству правильного шестиугольника большая его диагональ в два раза больше его стороны. Следовательно, если (AB=a), то (AD=BF=CE=2a).
Т.к. эти диагонали делят правильный шестиугольник на 6 равносторонних треугольников, причем площадь каждого равна (frac{sqrt3}4 a^2), то площадь всего шестиугольника равна
[S=6cdot dfrac{sqrt3}4a^2=24sqrt3 quad Rightarrow quad a=4 quad Rightarrow
quad AD=2a=8.]
Ответ: 8
Задание
7
#666
Уровень задания: Равен ЕГЭ
Около правильного шестиугольника (ABCDEF) описана окружность с центром в точке (O). Расстояние от точки (O) до одной из его сторон равно (4sqrt{3}). Найдите радиус этой окружности.
Радиус описанной около правильного шестиугольника окружности равен стороне этого шестиугольника.
(OK) – высота в треугольнике (AOF), опущенная из (O). Так как расстояние от точки до прямой – это длина перпендикуляра, опущенного из этой точки на эту прямую, то (OK = 4sqrt{3}).
Пусть (R) – радиус описанной окружности, тогда (OF = R), (KF = 0,5R) (так как (OK) ещё и медиана), таким образом, по теореме Пифагора (R^2 = (0,5R)^2 + (4sqrt{3})^2), откуда (R = 8).
Ответ: 8
Теме «Правильный шестиугольник и его свойства» в ЕГЭ по математике традиционно отводится сразу несколько заданий. Причем в зависимости от условия от учащегося может требоваться как развернутый, так и краткий ответ. Именно поэтому в процессе подготовки к сдаче аттестационного испытания выпускникам непременно стоит научиться решать задачи на применение свойств этой фигуры, в которых необходимо найти ее стороны, диагонали, радиус окружности со вписанным правильным шестиугольником и т. д.
Восполнить пробелы в знаниях, «прокачать» навыки и улучшить собственные знания по данной теме вам поможет образовательный проект «Школково». Наши специалисты подготовили и изложили весь базовый материал для подготовки к ЕГЭ в максимально доступной форме.
Чтобы школьники могли успешно справляться с задачами по данной теме, мы рекомендуем повторить базовые понятия: каковы свойства правильного шестиугольника, описанного около окружности, как вычисляется его площадь, чему равны его углы и т. д. Весь необходимый материал вы найдете в разделе «Теоретическая справка». Он был разработан нашими сотрудники на основе богатого практического опыта.
Для закрепления полученных знаний предлагаем потренироваться в решении соответствующих задач, а также заданий по теме «Параллелограмм в ЕГЭ». Найти их вы сможете в разделе «Каталог». Для каждого упражнения на сайте представлены алгоритм решения и правильный ответ.
Готовиться к ЕГЭ школьники из Москвы и других городов могут в режиме онлайн. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». В дальнейшем к этому заданию можно будет вернуться и, к примеру, обсудить алгоритм его решения с преподавателем.

УСТАЛ? Просто отдохни