Как найти большую диагональ в прямом параллелепипеде – Сайт, где вы сможете решить свои вопросы

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,651
гуманитарные
33,653
юридические
17,917
школьный раздел
611,893
разное
16,900

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

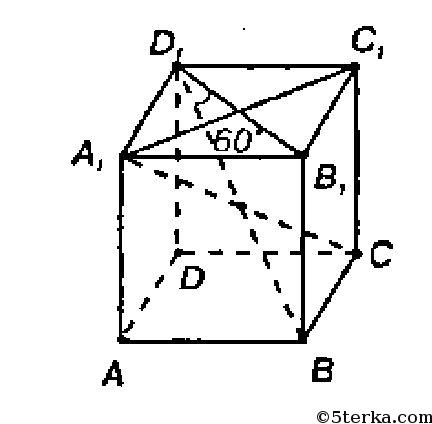
По условию A₁D₁= 3см, D₁C₁ = 5см, D₁B₁ = 4см. Так как основание является параллелограммом, а у параллелограмма сумма квадратов диагоналей равна сумме квадратов его сторон, то 2 А₁В₁² + 2 ⋅ A₁D₁² =

=A₁C₁²+B₁D₁².

Так что:

Так что А₁C₁>D₁B₁, а значит, диагональ BD — меньшая, а А₁С — большая.

Далее, в ΔCC₁A₁ по теореме Пифагора:

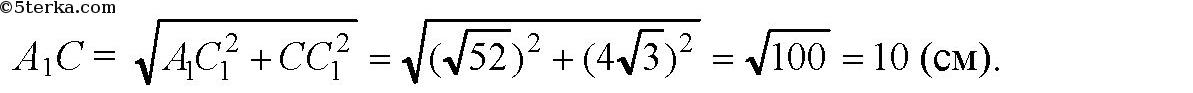
Ответ: 10 см.

Источник:

Домашняя работа по геометрии за 11 класс к учебнику «Геометрия. 10-11 класс» А.В. Погорелов

Решебник

по

геометрии

за 11 класс (А.В. Погорелов, 2001 год),
задача №31
к главе «§ 20. Многогранники».

Все задачи

← 30. В прямом параллелепипеде стороны основания 3 см и 8 см, угол между ними 60°. Боковая поверхность равна 220 см2. Найдите полную поверхность.

32. Найдите диагонали прямого параллелепипеда, у которого каждое ребро равно а, а угол основания равен 60°. →

Комментарии

Источник

Параллелепипед – это частный случай призмы, в основании которой лежит прямоугольник с длиной a и шириной b. Двигаясь по вертикальной или наклонной оси на определенную высоту c, данный прямоугольник создает объемное тело, именуемое параллелепипедом.

Параллелепипед по определению может быть наклонным или прямым, то есть угол между высотой и прямоугольником в основании варьируется от 0 до 90 градусов. Прямой параллелепипед имеет в качестве граней исключительно прямоугольники, и даже иногда квадрат (в основании), поэтому решение задач с его участием значительно облегчено. В случае с наклонным параллелепипедом в формулах необходимо учитывать, что боковой гранью является параллелограмм, строение которого зависит также от угла его наклона.

Помимо трех вышеуказанных параметров параллелепипеда – длины, ширины высоты, являющихся его ребрами, в данном теле можно также провести еще несколько отрезков, соединяющих его вершины. Как и в геометрических фигурах на плоскости, линии, проходящие внутри основного каркаса через вершины, называются диагоналями. Диагонали боковых граней прямоугольного параллелепипеда идентичны диагоналям прямоугольников, которыми представлены грани – их, соответственно, можно вычислить, используя подходящий онлайн калькулятор для прямоугольников.

Другое дело – диагональ, проходящая не по внешней поверхности прямоугольного параллелепипеда, а сквозь него, соединяя противоположные вершины верхнего и нижнего оснований. При этом, какая именно пара противоположных вершин соединена, не имеет значения для расчетов, так как если рассмотреть сечения, можно увидеть, что обе диагонали параллелепипеда идентичны и найти их можно одним и тем же способом.

Итак, для того чтобы вывести формулу диагонали через длину, ширину и высоту, необходимо заключить диагональ в плоскую геометрическую фигуру, свойства которой можно будет использовать. Для этого в любом основании – верхнем или нижнем, проводится диагональ, которая образует с диагональю параллелепипеда и боковым ребром (высотой) прямоугольный треугольник. Применив одну лишь теорему Пифагора, можно найти диагональ основания через ширину и длину,а затем диагональ прямоугольного параллелепипеда, добавив в расчеты высоту.

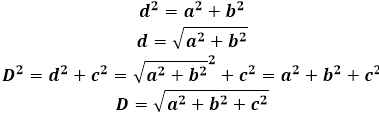
Используя последнюю и предпоследнюю формулу, можно также успешно найти длину, ширину или высоту прямоугольного параллелепипеда, имея в заданных условиях три параметра из четырех, включая диагональ параллелепипеда.
Например: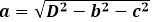

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также

Источник

Аркадий Панов

Ученик

(91),
закрыт

13 лет назад

а острый угол основания равен 60 градусов.

Elena Schatz

Высший разум

(140343)

13 лет назад

Пусть АВСДА1В1С1Д1-данный пар-пед, АВ=ВС=СС1=5 см, угол А=60 гр.
Найти: АС1
Решение:
1)Угол В=180-60=120(как углы пар-ма, прилеж. к одной стороне) .
Рассмотрим тр-к АВС: АС²=AB²+BC²-2AB*BC*cosВ; AC²=5²+5²-2*5*5*cos120;AC²=50+50*cos60;
AC²=75.
2)рассмотрим тр-к АС1С: AC1²=AC²+CC1²=>AC1²=75+25=100=>AC1=10(см) .
Ответ: 10 см.

Источник

Ответ:

Диагональ параллелепипеда равна 26 см.

Объяснение:

Пусть дан прямой параллелепипед $ABCDA_{1} B_{1} C_{1} D_{1}$ .

Основание параллелепипеда параллелограмм ABCD

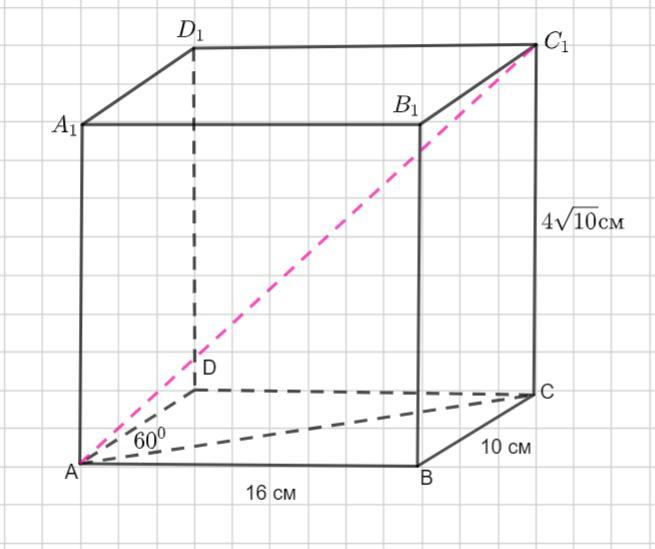
АВ = 16 см, ВС =10 см , ∠ А= 60°.

Надо найти большую диагональ параллелепипеда. Она опирается на большую диагональ параллелограмма.

Сумма углов параллелограмма при параллельных прямых равна 180°. Тогда ∠В =180°-60°=120°.

Найдем диагональ АС параллелограмма из Δ АВС по теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

$AC^{2} =AB^{2} +BC^{2} -2ABcdot BCcdot cos B;\AC^{2} =16^{2} +10^{2} -2cdot 16cdot 10cdot cos120^{0}=256+100 -2cdot160cdotleft(-dfrac{1}{2}right) =\=356+160=516;$

$AC= sqrt{516}$ см.

Рассмотрим Δ $ACC_{1}$ – прямоугольный . Найдем диагональ параллелепипеда по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AC_{1} ^{2} =AC^{2} +CC_{1} ^{2} ;\AC_{1}=sqrt{AC^{2} +CC_{1} ^{2}} ;\AC_{1}=sqrt{(sqrt{516} )+(4sqrt{10})^{2} } =sqrt{516+16cdot10} =sqrt{516+160} =sqrt{676} =26$