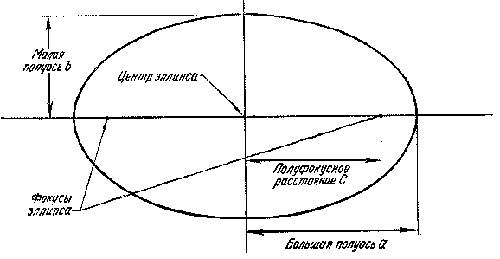
Как найти большую полуось эллиптической орбиты - Сайт, где вы сможете решить свои вопросы

Большая полуось — один из основных геометрических параметров объектов, образованных посредством конического сечения.

Эллипс[править | править код]

Основные параметры эллипса. Большая полуось обозначена как .

Большой осью эллипса называется его наибольший диаметр — отрезок проходящий через центр и два фокуса. Большая полуось составляет половину этого расстояния и идёт от центра эллипса к его краю через фокус.

Под углом в 90° к большой полуоси располагается малая полуось — минимальное расстояние от центра эллипса до его края. У частного случая эллипса — круга — большая и малая полуоси равны и являются радиусами. Таким образом, можно рассматривать большую и малую полуоси как некоего рода радиусы эллипса.

Длина большой полуоси связана с длиной малой полуоси через эксцентриситет , фокальный параметр и фокальное расстояние (полурасстояние между фокусами) следующим образом:

${displaystyle b=a{sqrt {1-e^{2}}},}$

${displaystyle p=a(1-e^{2}),}$

${displaystyle ap=b^{2}.}$

${displaystyle a^{2}=b^{2}+c^{2}}$

Большая полуось представляет собой среднее арифметическое между расстояниями от любой точки эллипса до его фокусов.

Рассмотрев уравнение в полярных координатах, с точкой в начале координат (полюс) и лучом, начинающейся из этой точки (полярная ось):

Получим средние значения и
и большую полуось ${displaystyle a={p over 1-e^{2}}.}$

Парабола[править | править код]

График построения параболы простейшей функции y = x²

Параболу можно получить как предел последовательности эллипсов, где один фокус остаётся постоянным, а другой отодвигается в бесконечность, сохраняя постоянным. Таким образом и стремятся к бесконечности, причём быстрее, чем .

Гипербола[править | править код]

Большая полуось гиперболы составляет половину минимального расстояния между двумя ветвями гиперболы, на положительной и отрицательной сторонах оси (слева и справа относительно начала координат). Для ветви расположенной на положительной стороне, полуось будет равна:

${frac {left(x-hright)^{2}}{a^{2}}}-{frac {left(y-kright)^{2}}{b^{2}}}=1.$

Если выразить её через коническое сечение и эксцентриситет, тогда выражение примет вид:

${displaystyle a={p over e^{2}-1}}$

Прямая, содержащая большую ось гиперболы, называется поперечной осью гиперболы.^[1]

Астрономия[править | править код]

Орбитальный период[править | править код]

В небесной механике орбитальный период обращения малых тел по эллиптической или круговой орбите вокруг более крупного центрального тела рассчитывается по формуле:

$T=2pi {sqrt {a^{3} over mu }}$

где:

— это размер большой полуоси орбиты

— это стандартный гравитационный параметр (произведение гравитационной постоянной на массу объекта

)

Следует обратить внимание, что в данной формуле для всех эллипсов период обращения определяется значением большой полуоси, независимо от эксцентриситета.

В астрономии большая полуось, наряду с орбитальным периодом, является одним из самых важных орбитальных элементов орбиты космического тела.

Для объектов Солнечной системы большая полуось связана с орбитальным периодом по третьему закону Кеплера.

$frac{T_1^2}{T_2^2} = frac{a_1^3}{a_2^3}$

где:

— орбитальный период в годах;

— большая полуось в астрономических единицах.

Это выражение является частным случаем общего решения задачи двух тел Исаака Ньютона:

${displaystyle T^{2}={frac {4pi ^{2}}{G(M+m)}}a^{3}}$

где:

— гравитационная постоянная

— масса центрального тела

— масса обращающегося вокруг него спутника. Как правило, масса спутника настолько мала по сравнению с массой центрального тела, что ею можно пренебречь. Поэтому, сделав соответствующие упрощения в этой формуле, получим данную формулу в упрощённом виде, который приведён выше.

Орбита движения спутника вокруг общего с центральным телом центра масс (барицентра), представляет собой эллипс. Большая полуось используется в астрономии всегда применительно к среднему расстоянию между планетой и звездой, в результате орбиты планет Солнечной системы приведены к гелиоцентрической системе, а не к системе движения вокруг центра масс. Эту разницу удобнее всего проиллюстрировать на примере системы Земля—Луна. Отношение масс в этом случае составляет 81,30059. Большая полуось геоцентрической орбиты Луны составляет 384 400 км, в то время как расстояние до Луны относительно центра масс системы Земля—Луна составляет 379 730 км — из-за влияния массы Луны центр масс находится не в центре Земли, а на расстоянии 4670 км от него. В итоге средняя орбитальная скорость Луны относительно центра масс составляет 1,010 км/с, а средняя скорость Земли — 0,012 км/с. Сумма этих скоростей даёт орбитальную скорость Луны 1,022 км/с; то же самое значение можно получить, рассматривая движение Луны относительно центра Земли, а не центра масс.

Среднее расстояние[править | править код]

Часто говорят, что большая полуось является средним расстоянием между центральным и орбитальным телом. Это не совсем верно, так как под средним расстоянием можно понимать разные значения — в зависимости от величины, по которой производят усреднение:

усреднение по эксцентрической аномалии. В таком случае среднее расстояние будет точно равно большой полуоси орбиты.
усреднение по истинной аномалии, тогда среднее расстояние будет точно равно малой полуоси орбиты.
усреднение по средней аномалии даст значение среднего расстояния, усреднённое по времени:

${displaystyle aleft(1+{frac {e^{2}}{2}}right).}$

усреднение по радиусу, которое получают из следующего соотношения:

${displaystyle {sqrt {ab}}=a{sqrt[{4}]{1-e^{2}}}.}$

Энергия; расчёт большой полуоси методом векторов состояния[править | править код]

В небесной механике большая полуось может быть рассчитана методом векторов орбитального состояния:

{displaystyle a={-mu over {2varepsilon }}}

для эллиптических орбит

для гиперболической траектории

$varepsilon ={v^{2} over {2}}-{mu over left|{mathbf {r}}right|}$

(удельная орбитальная энергия)

(стандартный гравитационный параметр),
где:

— орбитальная скорость спутника, на основе вектора скорости,

— вектор положения спутника в координатах системы отсчёта, относительно которой должны быть вычислены элементы орбиты (например, геоцентрический в плоскости экватора — на орбите вокруг Земли, или гелиоцентрический в плоскости эклиптики — на орбите вокруг Солнца),

— гравитационная постоянная,

— массы тел.

Большая полуось рассчитывается на основе общей массы и удельной энергии, независимо от значения эксцентриситета орбиты.

Большие и малые полуоси орбит планет[править | править код]

Орбиты планет всегда приводятся в качестве главных примеров эллипсов (первый закон Кеплера). Однако минимальная разница между большой и малой полуосями показывает, что они практически круговые по внешнему виду. Эта разница (или соотношение) основывается на эксцентриситете и вычисляется как ${displaystyle a/b=1/{sqrt {1-e^{2}}}}$ , что для типичных эксцентриситетов планет дает очень малые значения. Причина предположения о значительной эллиптичности орбит, вероятно, кроется в гораздо большей разнице между афелием и перигелием. Эта разница (или соотношение) также основывается на эксцентриситете и рассчитывается как ${displaystyle r_{text{a}}/r_{text{p}}=(1+e)/(1-e)}$ . Из-за большой разницы между афелием и перигелием второй закон Кеплера легко изобразить графически.

	Эксцентриситет	Большая полуось a (а. е.)	Малая полуось b (а. е.)	Разница (%)	Перигелий (а. е.)	Афелий (а. е.)	Разница (%)
Меркурий	0.206	0.38700	0.37870	2.2	0.307	0.467	52
Венера	0.007	0.72300	0.72298	0.002	0.718	0.728	1.4
Земля	0.017	1.00000	0.99986	0.014	0.983	1.017	3.5
Марс	0.093	1.52400	1.51740	0.44	1.382	1.666	21
Юпитер	0.049	5.20440	5.19820	0.12	4.950	5.459	10
Сатурн	0.057	9.58260	9.56730	0.16	9.041	10.124	12
Уран	0.046	19.21840	19.19770	0.11	18.330	20.110	9.7
Нептун	0.010	30.11000	30.10870	0.004	29.820	30.400	1.9

См. также[править | править код]

Элементы орбиты
Кеплеровы элементы орбиты
Эксцентриситет
Апоцентр и перицентр

Примечания[править | править код]

↑ 7.1 Alternative Characterization. Дата обращения: 15 сентября 2010. Архивировано 24 октября 2018 года.

Ссылки[править | править код]

Semi-major and semi-minor axes of an ellipse Архивная копия от 2 апреля 2012 на Wayback Machine With interactive animation

Источник

From Wikipedia, the free encyclopedia

Animation of Orbit by eccentricity
0.0 ·

0.2 ·

0.4 ·

0.6 ·

0.8

Two bodies with similar mass orbiting around a common barycenter with elliptic orbits.

Two bodies with unequal mass orbiting around a common barycenter with circular orbits.

Two bodies with highly unequal mass orbiting a common barycenter with circular orbits.

An elliptical orbit is depicted in the top-right quadrant of this diagram, where the gravitational potential well of the central mass shows potential energy, and the kinetic energy of the orbital speed is shown in red. The height of the kinetic energy decreases as the orbiting body’s speed decreases and distance increases according to Kepler’s laws.

In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 (thus excluding the circular orbit). In a wider sense, it is a Kepler orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1.

In a gravitational two-body problem with negative energy, both bodies follow similar elliptic orbits with the same orbital period around their common barycenter. Also the relative position of one body with respect to the other follows an elliptic orbit.

Examples of elliptic orbits include: Hohmann transfer orbit, Molniya orbit, and tundra orbit.

Velocity[edit]

Under standard assumptions, no other forces acting except two spherically symmetrical bodies m₁ and m₂,^[1] the orbital speed () of one body traveling along an elliptic orbit can be computed from the vis-viva equation as:^[2]

{displaystyle v={sqrt {mu left({2 over {r}}-{1 over {a}}right)}}}

where:

The velocity equation for a hyperbolic trajectory has either + , or it is the same with the convention that in that case a is negative.

Orbital period[edit]

Under standard assumptions the orbital period( T,! ) of a body travelling along an elliptic orbit can be computed as:^[3]

$T=2pisqrt{a^3over{mu}}$

where:

Conclusions:

The orbital period is equal to that for a circular orbit with the orbital radius equal to the semi-major axis (),
For a given semi-major axis the orbital period does not depend on the eccentricity (See also: Kepler’s third law).

Energy[edit]

Under standard assumptions, the specific orbital energy ( epsilon ) of an elliptic orbit is negative and the orbital energy conservation equation (the Vis-viva equation) for this orbit can take the form:^[4]

${v^2over{2}}-{muover{r}}=-{muover{2a}}=epsilon<0$

where:

Conclusions:

For a given semi-major axis the specific orbital energy is independent of the eccentricity.

Using the virial theorem we find:

the time-average of the specific potential energy is equal to −2ε
- the time-average of r⁻¹ is a⁻¹
the time-average of the specific kinetic energy is equal to ε

Energy in terms of semi major axis[edit]

It can be helpful to know the energy in terms of the semi major axis (and the involved masses). The total energy of the orbit is given by

${displaystyle E=-G{frac {Mm}{2a}}}$

where a is the semi major axis.

Derivation[edit]

Since gravity is a central force, the angular momentum is constant:

{displaystyle {dot {mathbf {L} }}=mathbf {r} times mathbf {F} =mathbf {r} times F(r)mathbf {hat {r}} =0}

At the closest and furthest approaches, the angular momentum is perpendicular to the distance from the mass orbited, therefore:

The total energy of the orbit is given by^[5]

${displaystyle E={frac {1}{2}}mv^{2}-G{frac {Mm}{r}}}$

We may substitute for v and obtain

${displaystyle E={frac {1}{2}}{frac {L^{2}}{mr^{2}}}-G{frac {Mm}{r}}}$

This is true for r being the closest / furthest distance so we get two simultaneous equations which we solve for E:

${displaystyle E=-G{frac {Mm}{r_{1}+r_{2}}}}$

Since ${textstyle r_{1}=a+aepsilon }$ and ${displaystyle r_{2}=a-aepsilon }$ , where epsilon is the eccentricity of the orbit, we finally have the stated result.

Flight path angle[edit]

The flight path angle is the angle between the orbiting body’s velocity vector (= the vector tangent to the instantaneous orbit) and the local horizontal. Under standard assumptions of the conservation of angular momentum the flight path angle phi satisfies the equation:^[6]

where:

psi is the angle between the orbital velocity vector and the semi-major axis. is the local true anomaly. ${displaystyle phi =nu +{frac {pi }{2}}-psi }$ , therefore,

${displaystyle cos phi =sin(psi -nu )=sin psi cos nu -cos psi sin nu ={frac {1+ecos nu }{sqrt {1+e^{2}+2ecos nu }}}}$

${displaystyle tan phi ={frac {esin nu }{1+ecos nu }}}$

where is the eccentricity.

The angular momentum is related to the vector cross product of position and velocity, which is proportional to the sine of the angle between these two vectors. Here phi is defined as the angle which differs by 90 degrees from this, so the cosine appears in place of the sine.

This section needs expansion. You can help by adding to it. (June 2008)

Equation of motion[edit]

From initial position and velocity[edit]

An orbit equation defines the path of an orbiting body $m_{2},!$ around central body $m_{1},!$ relative to $m_{1},!$ , without specifying position as a function of time. If the eccentricity is less than 1 then the equation of motion describes an elliptical orbit. Because Kepler’s equation has no general closed-form solution for the Eccentric anomaly (E) in terms of the Mean anomaly (M), equations of motion as a function of time also have no closed-form solution (although numerical solutions exist for both).

However, closed-form time-independent path equations of an elliptic orbit with respect to a central body can be determined from just an initial position () and velocity ().

For this case it is convenient to use the following assumptions which differ somewhat from the standard assumptions above:

The central body’s position is at the origin and is the primary focus () of the ellipse (alternatively, the center of mass may be used instead if the orbiting body has a significant mass)
The central body’s mass (m1) is known
The orbiting body’s initial position() and velocity() are known
The ellipse lies within the XY-plane

The fourth assumption can be made without loss of generality because any three points (or vectors) must lie within a common plane. Under these assumptions the second focus (sometimes called the “empty” focus) must also lie within the XY-plane: ${displaystyle mathbf {F2} =left(f_{x},f_{y}right)}$ .

Using vectors[edit]

The general equation of an ellipse under these assumptions using vectors is:

{displaystyle |mathbf {F2} -mathbf {p} |+|mathbf {p} |=2aqquad mid z=0}

where:

The semi-major axis length (a) can be calculated as:

${displaystyle a={frac {mu |mathbf {r} |}{2mu -|mathbf {r} |mathbf {v} ^{2}}}}$

where ${displaystyle mu =Gm_{1}}$ is the standard gravitational parameter.

The empty focus ( ${displaystyle mathbf {F2} =left(f_{x},f_{y}right)}$ ) can be found by first determining the Eccentricity vector:

${displaystyle mathbf {e} ={frac {mathbf {r} }{|mathbf {r} |}}-{frac {mathbf {v} times mathbf {h} }{mu }}}$

Where is the specific angular momentum of the orbiting body:^[7]

{displaystyle mathbf {h} =mathbf {r} times mathbf {v} }

Then

{displaystyle mathbf {F2} =-2amathbf {e} }

Using XY Coordinates[edit]

This can be done in cartesian coordinates using the following procedure:

The general equation of an ellipse under the assumptions above is:

${displaystyle {sqrt {left(f_{x}-xright)^{2}+left(f_{y}-yright)^{2}}}+{sqrt {x^{2}+y^{2}}}=2aqquad mid z=0}$

Given:

${displaystyle r_{x},r_{y}quad }$

the initial position coordinates

${displaystyle v_{x},v_{y}quad }$

the initial velocity coordinates

and

${displaystyle mu =Gm_{1}quad }$

the gravitational parameter

Then:

${displaystyle h=r_{x}v_{y}-r_{y}v_{x}quad }$

specific angular momentum

${displaystyle r={sqrt {r_{x}^{2}+r_{y}^{2}}}quad }$

initial distance from F1 (at the origin)

${displaystyle a={frac {mu r}{2mu -rleft(v_{x}^{2}+v_{y}^{2}right)}}quad }$

the semi-major axis length

${displaystyle e_{x}={frac {r_{x}}{r}}-{frac {hv_{y}}{mu }}quad }$

the Eccentricity vector coordinates

${displaystyle e_{y}={frac {r_{y}}{r}}+{frac {hv_{x}}{mu }}quad }$

Finally, the empty focus coordinates

${displaystyle f_{x}=-2ae_{x}quad }$

${displaystyle f_{y}=-2ae_{y}quad }$

Now the result values fx, fy and a can be applied to the general ellipse equation above.

Orbital parameters[edit]

The state of an orbiting body at any given time is defined by the orbiting body’s position and velocity with respect to the central body, which can be represented by the three-dimensional Cartesian coordinates (position of the orbiting body represented by x, y, and z) and the similar Cartesian components of the orbiting body’s velocity. This set of six variables, together with time, are called the orbital state vectors. Given the masses of the two bodies they determine the full orbit. The two most general cases with these 6 degrees of freedom are the elliptic and the hyperbolic orbit. Special cases with fewer degrees of freedom are the circular and parabolic orbit.

Because at least six variables are absolutely required to completely represent an elliptic orbit with this set of parameters, then six variables are required to represent an orbit with any set of parameters. Another set of six parameters that are commonly used are the orbital elements.

Solar System[edit]

In the Solar System, planets, asteroids, most comets and some pieces of space debris have approximately elliptical orbits around the Sun. Strictly speaking, both bodies revolve around the same focus of the ellipse, the one closer to the more massive body, but when one body is significantly more massive, such as the sun in relation to the earth, the focus may be contained within the larger massing body, and thus the smaller is said to revolve around it. The following chart of the perihelion and aphelion of the planets, dwarf planets and Halley’s Comet demonstrates the variation of the eccentricity of their elliptical orbits. For similar distances from the sun, wider bars denote greater eccentricity. Note the almost-zero eccentricity of Earth and Venus compared to the enormous eccentricity of Halley’s Comet and Eris.

Distances of selected bodies of the Solar System from the Sun. The left and right edges of each bar correspond to the perihelion and aphelion of the body, respectively, hence long bars denote high orbital eccentricity. The radius of the Sun is 0.7 million km, and the radius of Jupiter (the largest planet) is 0.07 million km, both too small to resolve on this image.

Radial elliptic trajectory[edit]

A radial trajectory can be a double line segment, which is a degenerate ellipse with semi-minor axis = 0 and eccentricity = 1. Although the eccentricity is 1, this is not a parabolic orbit. Most properties and formulas of elliptic orbits apply. However, the orbit cannot be closed. It is an open orbit corresponding to the part of the degenerate ellipse from the moment the bodies touch each other and move away from each other until they touch each other again. In the case of point masses one full orbit is possible, starting and ending with a singularity. The velocities at the start and end are infinite in opposite directions and the potential energy is equal to minus infinity.

The radial elliptic trajectory is the solution of a two-body problem with at some instant zero speed, as in the case of dropping an object (neglecting air resistance).

History[edit]

The Babylonians were the first to realize that the Sun’s motion along the ecliptic was not uniform, though they were unaware of why this was; it is today known that this is due to the Earth moving in an elliptic orbit around the Sun, with the Earth moving faster when it is nearer to the Sun at perihelion and moving slower when it is farther away at aphelion.^[8]

In the 17th century, Johannes Kepler discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun at one focus, and described this in his first law of planetary motion. Later, Isaac Newton explained this as a corollary of his law of universal gravitation.

References[edit]

^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. pp. 11–12. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Lissauer, Jack J.; de Pater, Imke (2019). Fundamental Planetary Sciences: physics, chemistry, and habitability. New York, NY, USA: Cambridge University Press. pp. 29–31. ISBN 9781108411981.
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 33. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. pp. 27–28. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 15. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 18. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 17. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ David Leverington (2003), Babylon to Voyager and beyond: a history of planetary astronomy, Cambridge University Press, pp. 6–7, ISBN 0-521-80840-5

Sources[edit]

D’Eliseo, Maurizio M. (2007). “The First-Order Orbital Equation”. American Journal of Physics. 75 (4): 352–355. Bibcode:2007AmJPh..75..352D. doi:10.1119/1.2432126.
D’Eliseo, Maurizio M.; Mironov, Sergey V. (2009). “The Gravitational Ellipse”. Journal of Mathematical Physics. 50 (2): 022901. arXiv:0802.2435. Bibcode:2009JMP….50a2901M. doi:10.1063/1.3078419.
Curtis, Howard D. (2019). Orbital Mechanics for Engineering Students (4th ed.). Butterworth-Heinemann. ISBN 978-0-08-102133-0.

External links[edit]

Java applet animating the orbit of a satellite in an elliptic Kepler orbit around the Earth with any value for semi-major axis and eccentricity.
Apogee – Perigee Lunar photographic comparison
Aphelion – Perihelion Solar photographic comparison
http://www.castor2.ca

Источник

Большая полуось (a) и малая полуось (b) эллипса

В геометрии большая ось эллипса – это его самый длинный диаметр : отрезок линии, который проходит через центр и оба фокусы с концами в самых широких точках периметра .

Большая полуось составляет половину большой оси и, таким образом, проходит от центра через фокус и по периметру. Малая полуось эллипса или гиперболы – это отрезок прямой, который находится под прямым углом с большой полуосью и имеет один конец в центре конического участка. В частном случае окружности длины обеих полуосей равны радиусу окружности.

Длина большой полуоси a эллипса связана с длиной малой полуоси b через эксцентриситет e и прямую полуось ℓ { displaystyle ell} ell следующим образом:

b = a 1 – e 2, ℓ = a (1 – e 2), a ℓ = b 2. { displaystyle { begin {align} b = a { sqrt {1-e ^ {2}}}, \ ell = a left (1-e ^ {2} right), , a ell = b ^ {2}. end {align}}}

${ displaystyle { begin {align} b = a { sqrt {1-e ^ {2}}}, \ ell = a left (1-e ^ {2} right), , \ a ell = b ^ {2}. End {выравнивается}}}$

Большая полуось гиперболы , в зависимости от соглашения, составляет плюс или минус половина расстояние между двумя ветвями. Таким образом, это расстояние от центра до любой вершины гиперболы.

A парабола может быть получена как предел последовательности эллипсов, в которой один фокус фиксируется, а другой может перемещаться произвольно далеко в одном направлении, сохраняя ℓ { displaystyle ell} ell исправлено. Таким образом, a и b стремятся к бесконечности, а быстрее, чем b.

Большая и малая оси – это оси симметрии кривой: в эллипсе малая ось является более короткой; в гиперболе это тот, который не пересекает гиперболу.

Содержание

1 Эллипс
2 Гипербола
3 Астрономия
- 3,1 Период обращения
- 3,2 Среднее расстояние
- 3,3 Энергия; вычисление большой полуоси из векторов состояния
- 3.4 Большая и малая полуоси планет
4 См. также
5 Ссылки
6 Внешние ссылки

Эллипс

Уравнение эллипса:

(x – h) 2 a 2 + (y – k) 2 b 2 = 1. { displaystyle { frac { left (xh right) ^ {2}} {a ^ {2}}} + { frac { left (yk right) ^ {2}} {b ^ {2}}} = 1.}

${ displaystyle { frac { left (xh right) ^ {2}} {a ^ {2}}} + { frac { left ( yk right) ^ {2}} {b ^ {2}}} = 1.}$

где (h, k) – центр эллипс в декартовых координатах, в котором произвольная точка задается как (x, y).

Большая полуось – это среднее значение максимального и минимального расстояний r max { displaystyle r _ { max}} ${ displaystyle r _ { max}}$ и r min { displaystyle r _ { min}} ${ displaystyle r _ { min}}$ эллипса от фокуса – то есть расстояний от фокуса до конечных точек большой оси. В астрономии эти крайние точки называются апсидами.

a = r max + r min 2. { displaystyle a = { frac {r _ { max} + r _ { min}} {2}}.}

${ displaystyle a = { frac {r _ { max} + r _ { min}} {2}}.}$

Малая полуось эллипса – это среднее геометрическое этих расстояния:

b = r max r min. { displaystyle b = { sqrt {r _ { max} r _ { min}}}.}

${ displaystyle b = { sqrt { r _ { max} r _ { min}}}.}$

эксцентриситет эллипса определяется как

e = 1 – b 2 a 2 { displaystyle e = { sqrt {1 – { frac {b ^ {2}} {a ^ {2}}}}}}

${ displaystyle e = { sqrt {1- { frac {b ^ {2}} {a ^ {2}}}}}}$ поэтому

r min = a (1 – e), r max = a (1 + e) { displaystyle r _ { min} = a (1-e), r _ { max} = a (1 + e)}

${ displaystyle r _ { min} = a (1-e), r _ { max} = а (1 + е)}$ .

Теперь рассмотрим уравнение в полярные координаты, с одним фокусом в начале координат, а другой в направлении (θ = π) – { displaystyle ( theta = pi) -},

г (1 + е соз ⁡ θ) = ℓ. { displaystyle r (1 + e cos theta) = ell. ,}

Среднее значение r = ℓ / (1 – e) { displaystyle r = ell / (1- e)}и r = ℓ / (1 + e) { displaystyle r = ell / (1 + e)}для θ = π { displaystyle theta = pi}и θ = 0 { displaystyle theta = 0}равно

a = ℓ 1 – e 2. { displaystyle a = { ell over 1-e ^ {2}}. ,}

$a = { ell over 1-e ^ {2}}. ,$

В эллипсе большая полуось – это среднее геометрическое расстояния от центра для фокусировки и расстояния от центра до любой директрисы.

Малая полуось эллипса проходит от центра эллипса (точка на полпути между фокусами и на линии между ними) до края эллипса. Малая полуось – это половина малой оси. Малая ось – это самый длинный отрезок прямой, перпендикулярный большой оси, который соединяет две точки на краю эллипса.

Малая полуось b связана с большой полуосью a через эксцентриситет e и прямую полуось ℓ { displaystyle ell} ell следующим образом:

b = a 1 – e 2 a ℓ = b 2. { displaystyle { begin {align} b = a { sqrt {1-e ^ {2}}} , ! \ a ell = b ^ {2}. , ! end {выровнено }}}

${ displaystyle { begin {align} b = a { sqrt {1 -e ^ {2}}} , ! \ a ell = b ^ {2}. , ! end {align}}}$

Длину малой полуоси можно также найти с помощью следующей формулы:

2 b = (p + q) 2 – f 2 { displaystyle 2b = { sqrt {(p + q) ^ {2} -f ^ {2}}}}

$2b = { sqrt {(p + q) ^ {2} -f ^ {2}} }$

где f – расстояние между фокусами, p и q – расстояния от каждого фокуса до любой точки эллипса.

Гипербола

Большая полуось гиперболы находится, в зависимости от соглашения, плюс или минус половина расстояния между двумя ветвями; если это a в направлении x, уравнение будет следующим:

(x – h) 2 a 2 – (y – k) 2 b 2 = 1. { displaystyle { frac { left (xh right) ^ {2}} {a ^ {2}}} – { frac { left (yk right) ^ {2}} {b ^ {2}}} = 1.}

${ frac { left (xh right) ^ {2}} {a ^ {2}}} - { frac { left (yk right) ^ {2}} { b ^ {2}}} = 1.$

В терминах полу -latus rectum и эксцентриситет мы имеем

a = ℓ e 2 – 1. { displaystyle a = { ell over e ^ {2} -1}.}

${ displaystyle a = { ell over e ^ {2} -1}.}$

Поперечная ось гиперболы совпадает с большой осью.

В гиперболе – сопряженная ось или малая ось Ось длины 2 b { displaystyle 2b}, соответствующая малой оси эллипса, может быть проведена перпендикулярно поперечной оси или большой оси, последняя соединяет две вершины (точки поворота) гиперболы, причем две оси пересекаются в центре гиперболы. Конечные точки (0, ± b) { displaystyle (0, pm b)}малой оси лежат на высоте асимптот над / под вершинами гиперболы. Любая половина малой оси называется малой полуосью длиной b. Обозначая длину большой полуоси (расстояние от центра до вершины) как a, длины малой и большой полуосей появляются в уравнении гиперболы относительно этих осей следующим образом:

x 2 a 2 – y 2 b 2 = 1. { displaystyle { frac {x ^ {2}} {a ^ {2}}} – { frac {y ^ {2}} {b ^ {2}}} = 1.}

${ frac {x ^ {2}} {a ^ { 2}}} - { frac {y ^ {2}} {b ^ {2}}} = 1.$

Малая полуось – это также расстояние от одного из фокусов гиперболы до асимптоты. Часто называемый параметром удара, он важен в физике и астрономии и позволяет измерить расстояние, на которое частица не попадет в фокус, если ее путешествие не будет нарушено телом в фокусе.

Малая полуось и большая полуось связаны через эксцентриситет следующим образом:

b = ae 2 – 1. { displaystyle b = a { sqrt {e ^ {2} -1}}.}

$b = a { sqrt {e ^ {2} -1}}.$

Обратите внимание, что в гиперболе b может быть больше a.

Астрономия

Орбитальная период

В астродинамике период обращения T малого тела, вращающегося вокруг центрального тела по круговой или эллиптической орбите, равен:

T = 2 π a 3 μ { displaystyle T = 2 pi { sqrt {a ^ {3} over mu}}}

$T = 2 pi { sqrt {a ^ {3} over mu}}$

где:

a – длина большой полуоси орбиты

μ { displaystyle mu}

– это стандартный гравитационный параметр центрального тела

. Обратите внимание, что для всех эллипсов с данной большой полуосью период обращения то же самое, несмотря на их эксцентричность.

удельный угловой момент h небольшого тела, вращающегося вокруг центрального тела по круговой или эллиптической орбите:

h = a μ (1 – e 2) { displaystyle h = { sqrt {a mu left (1-e ^ {2} right)}}}

${ displaystyle h = { sqrt {a mu left (1-е ^ {2} right)}}}$

где:

a и

μ { displaystyle mu}

определены выше e – эксцентриситет орбиты

В астрономии большая полуось является одной из наиболее важных орбитальных элементы орбиты вместе с его периодом обращения. Для объектов Солнечной системы большая полуось связана с периодом орбиты третьим законом Кеплера (первоначально эмпирически получено),

T 2 ∝ a 3 { displaystyle T ^ {2} propto a ^ {3} ,}

$T ^ {2 } propto a ^ {3} ,$

где T – период, а a – большая полуось. Эта форма оказывается упрощением общей формы для задачи двух тел, как определено Ньютоном :

T 2 = 4 π 2 G (M + m) a 3 { displaystyle T ^ {2} = { frac {4 pi ^ {2}} {G (M + m)}} a ^ {3} ,}

${ displaystyle T ^ {2} = { frac {4 pi ^ { 2}} {G (M + m)}} a ^ {3} ,}$

где G – гравитационная постоянная, M – масса центрального тела, а m – масса движущегося по орбите тела. Обычно масса центрального тела настолько больше, чем масса вращающегося тела, что m можно не принимать во внимание. Это предположение и использование типичных астрономических единиц приводит к более простой форме, которую открыл Кеплер.

Путь движущегося по орбите тела вокруг барицентра и его путь относительно его первичного элемента являются эллипсами. Большая полуось иногда используется в астрономии как расстояние между первичными и вторичными объектами, когда отношение масс первичного элемента к вторичному значительно велико (M ≫ m { displaystyle M gg m} M gg m ); таким образом, параметры орбит планет даны в гелиоцентрических терминах. Разницу между примоцентрическими и «абсолютными» орбитами лучше всего можно проиллюстрировать, взглянув на систему Земля – Луна. Соотношение масс в данном случае составляет 81,30059. Характерное расстояние Земля – Луна, большая полуось геоцентрической лунной орбиты, составляет 384 400 км. (Учитывая эксцентриситет лунной орбиты e = 0,0549, ее малая полуось составляет 383 800 км. Таким образом, орбита Луны почти круговая.) Барицентрическая лунная орбита, с другой стороны, имеет большую полуось 379 730 км, земную. встречная орбита, принимающая разницу, 4670 км. Средняя барицентрическая орбитальная скорость Луны составляет 1,010 км / с, а у Земли – 0,012 км / с. Сумма этих скоростей дает геоцентрическую среднюю орбитальную скорость Луны 1,022 км / с; такое же значение можно получить, рассматривая только значение большой геоцентрической полуоси.

Среднее расстояние

Часто говорят, что большая полуось – это «среднее» расстояние между основными фокус эллипса и вращающееся тело. Это не совсем точно, потому что это зависит от того, какое среднее значение берется за основу.

Усредненное по времени значение обратной величины радиуса, r – 1 { displaystyle r ^ {- 1}} ${ displaystyle r ^ {- 1}}$ , это a – 1 { displaystyle a ^ {- 1}} $a ^ {- 1}$ .

Энергия; вычисление большой полуоси из векторов состояния

В астродинамике большая полуось a может быть вычислена из векторов орбитального состояния :

a = – μ 2 ε { displaystyle a = – { mu over {2 varepsilon}} ,}

для эллиптической орбиты и, в зависимости от соглашения, то же самое или

a = μ 2 ε { displaystyle a = { mu over {2 varepsilon}} ,}

для гиперболической траектории и

ε = v 2 2 – μ | г | { displaystyle varepsilon = {v ^ {2} over {2}} – { mu over left | mathbf {r} right |}}

$varepsilon = {v ^ {2} over {2}} - { mu over left | mathbf {r} right |}$

(удельная орбитальная энергия ) и

μ = GM { displaystyle mu = GM ,}

(стандартный гравитационный параметр ), где:

v – орбитальная скорость от вектора скорости движущегося по орбите объекта,
rявляется декартовым вектором положения орбитального объекта в координатах системы отсчета, относительно которой должны быть вычислены элементы орбиты (например, геоцентрическая экваториальная для орбиты вокруг Земли или гелиоцентрическая эклиптика для орбиты вокруг Солнца),
G – гравитационная постоянная,,
M – масса гравитирующего тела, и
ε { displaystyle varepsilon}– это удельная энергия движущегося по орбите тела.

Обратите внимание, что для данного количества общей массы удельная энергия и большая полуось всегда одинаковы, независимо от эксцентриситета. или соотношение масс. И наоборот, для данной общей массы и большой полуоси общая удельная орбитальная энергия всегда одинакова. Это утверждение всегда будет верным при любых данных условиях.

Большая и полу-малая оси планет

Орбиты планет всегда приводятся в качестве ярких примеров эллипсов (первый пример Кеплера закон ). Однако минимальная разница между большой и малой полуосями показывает, что они практически круглые по внешнему виду. Эта разница (или соотношение) основывается на эксцентриситете и рассчитывается как ab = 1 1 – e 2 { displaystyle {{a} over {b}} = {1 over { sqrt {1-e ^ {2}}}}} ${ displaystyle {{a} over { b}} = {1 over { sqrt {1-e ^ {2}}}}}$ что для типичных эксцентриситетов планет дает очень маленькие результаты.

Причина предположения о выдающихся эллиптических орбитах, вероятно, кроется в гораздо большей разнице между афелием и перигелием. Эта разница (или соотношение) также зависит от эксцентриситета и рассчитывается как rarp = 1 + e 1 – e { displaystyle {{r _ { text {a}}} over {r _ { text {p }}}} = {{1 + e} over {1-e}}} ${ displaystyle {{ r _ { text {a}}} over {r _ { текст {p}}}} = {{1 + e} over {1-e}}}$ . Из-за большой разницы между афелием и перигелием второй закон Кеплера легко визуализируется.

Имя	Эксцентриситет	Большая полуось a (AU )	Малая полуось b (AU )	разница (%)	Перигелий (AU )	Афелий (AU )	разница (%)
Меркурий	0,206	0,38700	0,37870	2,2	0,307	0,467	52
Венера	0,007	0,72300	0,72298	0,002	0,718	0,728	1,4
Земля	0,017	1,00000	0,99986	0,014	0,983	1,017	3,5
Марс	0,093	1,52400	1,51740	0,44	1,382	1,666	21
Юпитер	0,049	5,20440	5,19820	0,12	4,950	5,459	10
Сатурн	0,057	9,58260	9,56730	0,16	9,041	10,124	12
Уран	0,046	19,21840	19,19770	0,11	18,330	20,110	9,7
Нептун	0,010	30.11000	30.10870	0.004	29.820	30.400	1.9

См. Также

Ссылки

Внешние ссылки

Источник

КЕПЛЕРОВСКИЕ ЗАКОНЫ ОРБИТАЛЬНОГО ДВИЖЕНИЯ

ПЕРВЫЙ ЗАКОН КЕПЛЕРА ОПИСЫВАЕТ ФОРМУ ОРБИТЫ

Орбита планеты вокруг Солнца (или спутника вокруг планеты) не идеальная окружность, а эллипс — “сплющенная” окружность. Солнце (или центр планеты) занимает один фокус эллипса. Фокус является одной из двух внутренних точек, которые помогают определить форму эллипса. Расстояние в сумме от одного фокуса к любой точке эллипса, а затем обратно ко второму фокусу всегда одно и то же.

ВТОРОЙ ЗАКОН КЕПЛЕРА ОПИСЫВАЕТ ИЗМЕНЕНИЕ СКОРОСТИ ОБЪЕКТА ПРИ ЕГО ДВИЖЕНИИ ПО ОРБИТЕ

Скорость планеты меняется в зависимости от того, насколько далеко она от Солнца. Чем она ближе, тем сильнее гравитационное притяжения, и тем быстрее планета движется. Чем она дальше от Солнца, тем гравитационное притяжение слабее, и тем медленнее движение планеты.

ТРЕТИЙ ЗАКОН ДВИЖЕНИЯ КЕПЛЕРА СРАВНИВАЕТ ДВИЖЕНИЯ ОБЪЕКТОВ ПРИ РАЗЛИЧНЫХ РАЗМЕРАХ ОТБИТ

Планета, находящаяся дальше от Солнца, не только имеет более длинный путь, чем более близкая, но и перемещается медленнее, поскольку гравитационное притяжение Солнца на него слабее. Таким образом, чем больше орбита планеты, тем больше времени нужно планете для еѐ прохождения.

ПЕРВЫЙ ЗАКОН КЕПЛЕРА: ЗАКОН ЭЛЛИПСОВ

Орбита спутника представляет собой эллипс, в одном из фокусов которого находится планета.

Эллипс определяется двумя фокусами и всеми точками, для которых сумма расстояний одинаковы. Большая полуось (a) – это наибольшее расстояние от центра до края эллипса. Если А и В – это расстояния от фокуса до любой точки эллипса, то А+ B = 2а. Короткая ось называется малой полуосью (b).

ВТОРОЙ ЗАКОН КЕПЛЕРА: ЗАКОН РАВНЫХ ПЛОЩАДЕЙ

За равные промежутки времени радиус-вектор, соединяющий спутник и планету, покрывает равные площади.

Находясь на эллиптической орбите, спутник иногда находится ближе к планете, чем в остальное время. Наиближайшая точка называется “перигей”. Точка наибольшего удаления от планеты — апогей. Второй закон Кепплера фактически говорит, что скорость спутника непостоянна — движение медленнее всего в апогее и быстрее всего в перигее.

ВТОРОЙ ЗАКОН КЕПЛЕРА

Площадь области синего цвета остаѐтся неизменной. Зелѐная стрелка – скорость. Фиолетовая стрелка, направленная в сторону Земли – ускорение. Две других фиолетовых стрелки – компоненты ускорения направленные параллельно и перпендикулярно к скорости.

ШЕСТЬ КЕПЛЕРОВСКИХ ЭЛЕМЕНТОВ

Нужно знать шесть значений, чтобы полностью определить орбиту. Этот набор из шести чисел называется спутниковыми орбитальными элементами, или иногда “кеплеровскими элементами” (в честь Иоганна Кеплера [1571-1630]), или даже просто элементами. Эти числа определяют эллипс, ориентируют его относительно Земли и помещают спутник на эллипс в определенный момент времени. В кеплеровской модели спутники крутятся по эллипсам постоянной формы и ориентации. Земля находится в одном из фокусов эллипса, не в центре (если эллипс орбиты не является идеальным кругом).

Реальный мир немного более сложен, чем модели Кеплера, и программы слежения компенсируют это за счет введения небольших изменений в кеплеровские модели. Эти поправки называют возмущениями. Возмущения, учитываемые любительскими программами слежения, обусловлены неравномерностью гравитационного поля Земли (которую, к счастью, вам не нужно указывать), а также влиянием на спутник атмосферы. Это влияние иногда называют седьмым, дополнительным орбитальным элементом.

АПОГЕЙ И ПЕРИГЕЙ

Апогеем (q) называется самое большое расстояние от Земли, на котором может находиться спутник. Также называют точку орбиты в которой спутник находится на самом большом расстоянии от Земли.

Перигеем (p) называется ближайшее расстояние от Земли. Аналогичным образом, называется точка орбиты спутника, ближайшая к Земле.

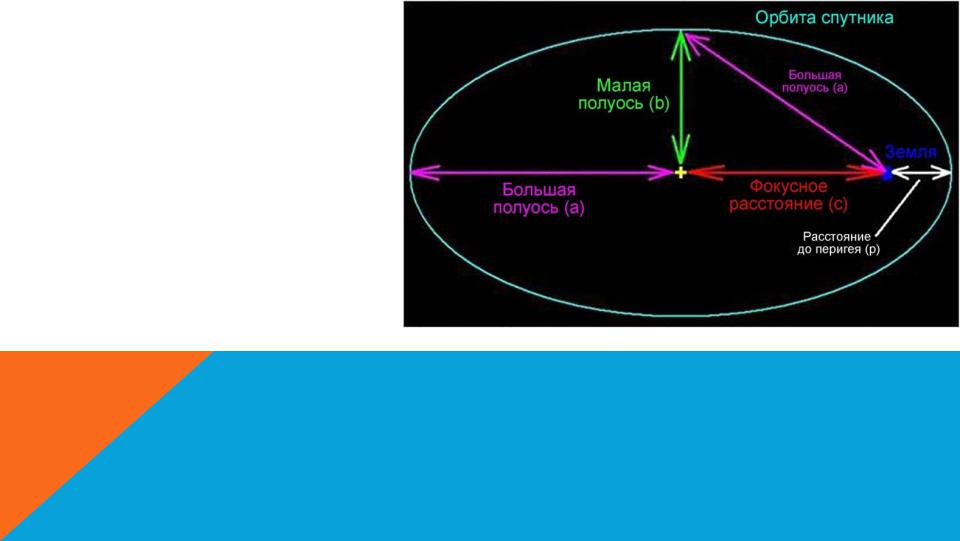
БОЛЬШАЯ И МАЛАЯ ПОЛУОСИ

Большая полуось (a): Расстояние от центра эллиптической орбиты до точки апогея или перигея. Она также определяется как среднее расстояние спутника до центра Земли.

Малая полуось(b): Ближайшее расстояние от истинного центра эллиптической орбиты до ее траектории.

Фокусное расстояние

(c): Расстояние от истинного центра эллиптической орбиты до центра Земли.

ЭКСЦЕНТРИСИТЕТ ОРБИТЫ

Эксцентриситет орбиты астрономического объекта — это параметр, который определяет величину, на которую его орбита отклоняется от идеальной окружности.Термин получил свое название от параметров конического сечения, а каждая кеплеровская орбита является коническим сечением.

Длина большой полуоси α эллипса связана с длиной малой полуоси b через эксцентриситета ε и коническое сечение l, а именно:

l a 1 2 , al b2

1 b2 a 2

КОНИЧЕСКИЕ СЕЧЕНИЯ

ГИПЕРБОЛА МОЖЕТ БЫТЬ ОПРЕДЕЛЕНА КАК КРИВАЯ, ПОЛУЧЕННАЯ ПЕРЕСЕЧЕНИЕМ ПРАВИЛЬНОЙ КРУГОВОЙ КОНИЧЕСКОЙ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ, ПЕРЕСЕКАЮЩЕЙ ОБЕ ПОЛОВИНЫ КОНУСА. ДРУГИЕ ОСНОВНЫЕ ВИДЫ КОНИЧЕСКИХ СЕЧЕНИЙ ЭТО ЭЛЛИПС И ПАРАБОЛА; В ЭТИХ СЛУЧАЯХ ПЛОСКОСТЬ ПЕРЕСЕКАЕТ ТОЛЬКО ОДНУ ПОЛОВИНУ ДВОЙНОГО КОНУСА. ЕСЛИ ПЛОСКОСТЬ ПРОХОДИТ ЧЕРЕЗ ВЕРШИНУ ДВОЙНОГО КОНУСА, ОБРАЗУЮТСЯ ВЫРОЖДЕННЫЕ ГИПЕРБОЛЫ – ДВЕ ПРЯМЫЕ ЛИНИИ, КОТОРЫЕ ПЕРЕСЕКАЮТСЯ В ТОЧКЕ ВЕРШИНЫ.

Источник

Для определения эллиптической орбиты, помимо величины большой полуоси, необходимо знать еще один из элементов орбиты — малую полуось b, полуфокусное расстояние с или эксцентриситет е. Эти величины связаны следующими соотношениями:

полуфокусное расстояние

с = ?a² — b²

эксцентриситет

Для искусственных спутников Земли очевидны также следующие соотношения:

средняя высота спутника над Землей

H_ср = a — 6378 км,

или где H_ап. — высота апогея орбиты;

H_пер.— высота перигея орбиты;

полуфокусное расстояние орбиты

Примеры использования формул

1. Определить элементы орбит советских искусственных спутников Земли по известным высотам апогея и перигея.

В соответствии с опубликованными данными примем следующие округленные значения для высот апогея и перигея советских искусственных спутников Земли:

H_пер. = 225 км (для всех трех спутников);[146]

H_ап.1 = 950 км, H_ап.2 = 1670 км, H_ап.3 = 1880 км.

Тогда средние высоты спутников над Землей будут равны:

для первого спутника H_ср1 =

для второго спутника H_ср2 =

^{Элементы эллиптической орбиты.}

для третьего спутника H_ср3 =

а полуфокусные расстояния соответственно:

Теперь можно определить величины больших и малых осей орбит:

a₁= H_ср1+6378 = 588 + 6378 = 6966 км,

а₂ = 948 + 6378 = 7326 км,

а₃ = 1053 + 6378 = 7431 км,

2. На сколько орбиты советских искусственных спутников Земли отличаются от круга?

Эксцентриситет орбит советских спутников весьма мал, то есть эллиптические орбиты спутников весьма мало отличаются от круга:

Действительно, разность полуосей орбит равна:

а₁ — b₁ = 6966–6955 = 11 км,

а₂ — b₂ = 7326–7290 = 36 км,

а₃ — b₃ = 7431–7385 = 46 км,

В масштабе чертежа, на котором схематически изображены орбиты советских спутников, эта разность неощутима, и орбиты практически становятся кругами.

^{Схематическое изображение орбит первых советских искусственных спутников Земли.}

Источник

Эллипс[править | править код]

Парабола[править | править код]

Гипербола[править | править код]

Астрономия[править | править код]

Орбитальный период[править | править код]

Среднее расстояние[править | править код]

Энергия; расчёт большой полуоси методом векторов состояния[править | править код]

Большие и малые полуоси орбит планет[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Velocity[edit]

Orbital period[edit]

Energy[edit]

Energy in terms of semi major axis[edit]

Derivation[edit]

Flight path angle[edit]

Equation of motion[edit]

From initial position and velocity[edit]

Using vectors[edit]

Using XY Coordinates[edit]

Orbital parameters[edit]

Solar System[edit]

Radial elliptic trajectory[edit]

History[edit]

See also[edit]

References[edit]

Sources[edit]

External links[edit]

Содержание

Эллипс

Гипербола

Астрономия

Орбитальная период

Среднее расстояние

Энергия; вычисление большой полуоси из векторов состояния

Большая и полу-малая оси планет

См. Также

Ссылки

Внешние ссылки

Вам также может понравиться

Опен офис как найти сумму

Как найти песню были ночи были дни

Звенит лад на гитаре как исправить

Добавить комментарий Отменить ответ