Сторона параллелограмма
Зная диагонали параллелограмма и одну его сторону, можно найти вторую сторону. Для этого нужно извлечь квадратный корень из половины суммы квадратов диагоналей без удвоенного квадрата известной стороны.
Другой способ как вычислить сторону параллелограмма требует высоты и противолежащего ей угла, тогда из прямоугольного треугольника, образованного высотой, сторона параллелограмма будет равна отношению высоты к синусу известного угла: 
Также высоту можно использовать при нахождении стороны параллелограмма через площадь. Так как площадь параллелограмма представляет собой произведение стороны и высоты, то сторона будет отношением площади к высоте, которая падает на эту сторону: 
Геометрические фигуры. Параллелограмм. Стороны, диагонали параллелограмма.
Формулы для вычисления длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:

2. Формула сторон параллелограмма через диагонали и вторую сторону:

3. Формула сторон параллелограмма через высоту и sin угла:

4. Формула сторон параллелограмма через площадь и высоту:

Диагонали параллелограмма.
Диагональю параллелограмма является каждый отрезок соединяющий 2 вершины противолежащих углов параллелограмма.
У параллелограмма есть 2 диагонали — длинная d1, и короткая — d2
Формулы вычисления длины диагонали параллелограмма:
1. Формулы диагоналей параллелограмма через стороны и cos β (из теоремы косинусов):

2. Формулы диагоналей параллелограмма через стороны и cos α (из теоремы косинусов):

3. Формула диагонали параллелограмма через 2 стороны и известную вторую диагональ:

4. Формула диагонали параллелограмма через площадь, диагональ которая известна, и угол между диагоналями:
Как найти большую сторону параллелограмма
Тип 3 № 49979 
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.
Это задание ещё не решено, приводим решение прототипа.
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
Заметим, что как накрест лежащие углы при пересечении параллельных прямых секущей. Значит, треугольник ADL − равнобедренный. Пусть тогда Противоположные стороны параллелограмма ABCD попарно равны, тогда
24
Июл 2013
Категория: 01 Геометрия
01. Параллелограмм
2013-07-24
2022-09-11
Задача 1. Сумма двух углов параллелограмма равна . Найдите один из оставшихся углов. Ответ дайте в градусах.

Решение: + показать
Задача 2. Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах.

Решение: + показать
Задача 3. Найдите больший угол параллелограмма, если два его угла относятся как Ответ дайте в градусах.

Решение: + показать
Задача 4. Диагональ параллелограмма образует с двумя его сторонами углы и
Найдите больший угол параллелограмма. Ответ дайте в градусах.
Решение: + показать
Задача 5. Периметр параллелограмма равен Меньшая сторона равна
Найдите большую сторону параллелограмма.

Решение: + показать
Задача 6. Две стороны параллелограмма относятся как а периметр его равен
Найдите большую сторону параллелограмма.

Решение: + показать
Задача 7. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна Найдите его большую сторону.

Решение: + показать
Задача 8. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
 Решение: + показать
Решение: + показать
Задача 9. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен

Решение: + показать
Задача 10. В параллелограмме высота, опущенная на сторону
из точки
равна
. Найдите синус угла
.
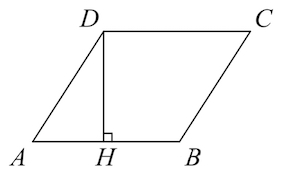
Решение: + показать
Задача 11. В параллелограмме
Найдите высоту, опущенную на сторону

Решение: + показать
Задача 12. В параллелограмме
Найдите большую высоту параллелограмма.
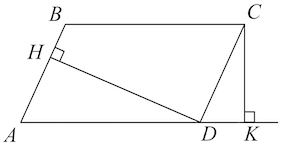
Решение: + показать
Задача 13. Площадь параллелограмма равна две его стороны равны
и
Найдите большую высоту этого параллелограмма.

Решение: + показать
Задача 14. В параллелограмме
. Найдите
.

Решение: + показать
Задача 15. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Решение: + показать
Задача 16. Площадь параллелограмма равна
Точка
— середина стороны
. Найдите площадь трапеции
.

Решение: + показать
Задача 17. Площадь параллелограмма равна
Найдите площадь параллелограмма
вершинами которого являются середины сторон данного параллелограмма.

Решение: + показать
Задача 18. Найдите диагональ параллелограмма
, если стороны квадратных клеток равны 1.

Решение: + показать
Задача 19. Диагонали четырехугольника равны и
Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
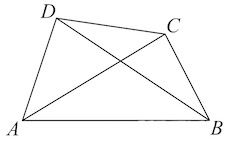
Решение: + показать

Вы можете пройти тест по теме «Параллелограмм. Вычисление углов и длин».
Автор: egeMax |
комментария 2
|
Как найти длину одной из сторон параллелограмма?
Чтобы найти сторону параллелограмма, необходимо наличие некоторых других значений, которые бы были известны. Далее попросту использовать одну из подходящих формул. Например, по теореме косинусов, это формулы сторон через диагонали и находящийся между ними угол:
Другим решением, являются формулы, где стороны рассчитываются по диагонали и одной из известной стороны:
Вот еще формулы сторон параллелепипеда, через вторую сторону, диагонали и косинус угла:
Стоит напомнить и про формулы длин сторон, через высоту и синус угла:
Так же длину стороны параллелограмма, можно определить если известны площадь и высота:
Как видим, вариантов расчета высоты параллелограмма достаточно много и хотелось напомнить основные характеристики этой геометрической фигуры: Во первых, параллелограммом называется четырехугольник, имеющий параллельно расположенные противоположные стороны , т. е. находящиеся на параллельных прямых. Квадраты, прямоугольники и ромбы, также являются параллелограммами. система выбрала этот ответ лучшим Для нахождения стороны параллелограмма есть более десятка разных формул (они перечислены в ответе автора Бульбозавр), но для решения задач на эту тему, далеко не всегда их можно применить. На мой взгляд лучше всего разобрать несколько примеров и на практике увидеть, как находить сторону этой фигуры – в наших случаях с помощью уравнений. Пример 1 Нужно найти стороны параллелограмма, если одна из сторон больше другой в два раза а периметр равен 30 см. Даже не нужно чертить рисунок, а просто составить уравнение и решить его периметр(30см) = 2(х+2х) откуда х=5см, следовательно одна сторона равна 5см, другая – 10см. Пример 2 АВСД – параллелограмм, нужно найти его стороны если – ВМ перпендикуляр к АС, АМ=6см, МС=15см, ВС больше АВ на 6 см
Для решения этой задачи сначала рассматриваем два прямоугольных треугольника АВМ и ВСМ у которых общий катет h. Согласно Пифагору h*h=a*a-6*6=b*b-15*15 откуда b*b-a*a=(b-a)(b+a)=225-36=189 по условию задачи b-a=7 тогда b+a=189/7=27 решив эту простенькую систему уравнений найдем стороны a=10см b=17cм Alexsandr82 6 лет назад Есть еще несколько формул которые будут скорее вспомогательными при решении задач по нахождению стороны паралелограмма но тем не менее их тоже нужно знать. Например одну из сторон паралеллограмма можно найти если известна вторая сторона и периметр фигуры по формуле: Р = 2(а+b), тогда а = (Р/2 – b), или b = (P/2 – a), где Р – периметр, а и b – стороны. Также можно найти сторону паралеллограмма зная его площадь и высоту опущенную на искомую сторону: S = a*H1 = b*H2, тогда а = S/H1 или b = S/H2, где S – площадь, а – меньшая сторона паралелограмма, b – большая сторона, Н1 – высота построенная к меньшей стороне, Н2 – сторна построенная к большей стороне паралеллограмма. Vector 60 8 месяцев назад Существует несколько формул для вычисления сторон параллелограмма (a и b). 1) Для нахождения сторон параллелограмма можно воспользоваться длиной диагоналей, а также величиной углов между диагоналями. Формулы будут такими:
2) Если известна одна из сторон и диагонали, то другую сторону можно найти так:
3) Если известна высота и величина одного из углов, то стороны параллелограмма можно найти по таким формулам:
4) Еще можно использовать значение площади и высоты:
Stasy12 более года назад Формул, конечно много, с помощью которых можно найти сторону параллелограмма. Например можно найти стороны паралелограмма, зная размеры диагоналей и угла между ними(формула 1и 2) Зная длины диагоналей и одну из сторон, легко можно найти вторую(формулы 3 и 4) Через высоту, которая опущена на сторону и угол между сторонами(формулы 5 и 6) Зная площадь и высоту, которая опущена на заданную сторону можно найти длину стороны(формулы 7 и 8).
Знаете ответ? |
Добрый вечер.
Первым делом я хочу предложить Вам вспомнить, что параллелограммом называют такой четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть они лежат на параллельных прямых. Разобравшись с этим, давайте подумаем как у нас может формироваться условие такой задачи.
На самом деле, вариантов достаточно много. Все даже невозможно перечислить. Но мы с Вами можем прорешать какой-то из них (как раз тот, который вы попросили). Но Вашего условия мне будет маловато. Давайте к примеру решим такую задачу, Нам дан параллелограмм ABCD, у которого AB = DС = 15 см и это будет меньшая сторона. А также нам известен периметр данного параллелограмма: 100 см. Нам нужно понять как найти большую сторону параллелограмма.
Исходя из знаний периметра, и того, что противоположные стороны равны, мы получаем следующее:
![]()
![]()
![]()
![]()
![]()
Надеюсь теперь Вам стало более понятно, как это можно сделать. Но ещё раз предупреждаем, что это не единый вариант постановки вопроса и условия задачи. будьте внимательны!
Ответ: ![]() см
см

Две стороны параллелограмма относятся
Дата: 2016-12-09
3234
Категория: Пл. Параллелограм
Метка: ЕГЭ-№1
27824. Две стороны параллелограмма относятся как 3:4, а периметр его равен 70. Найдите большую сторону параллелограмма.

Периметр фигуры это сумма всех её сторон. Введём коэффициент пропорциональности х, тогда меньшая сторона параллелограмма будет 3х, а большая сторона 4х. Можем записать:

Таким образом, меньшая сторона будет равна 3∙5=15, большая 4∙5=20.
Ответ: 20
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok












