Как найти большую сторону параллелограмма через периметр - Сайт, где вы сможете решить свои вопросы

Ант

Мыслитель

(7063)

13 лет назад

Прими меньшую сторону за х. Тогда большая будет (х+2). Составь уравнение: 2х + 2(х+2) = Р
Упрости его: 2х+2х+4 = Р
4х+4 = Р
х = (Р – 4) : 4

НАТИ

Профи

(877)

13 лет назад

раздели сумму на 4,получится сколько см все линии. и к двум значениям +2
например 80/4=20, значит 20+2=22, 2стороны по 20см и 2е по 22 см…

RazellПрофи (562)

13 лет назад

хех 2 стороны по 20 а две по 22? а теперь посчитай периметр… 84… тото и оно, что не так!

НАТИ
Профи
(877)
значит 18 и 22

Razell

Профи

(562)

13 лет назад

пусть a – меньшая сторона, а b большая, по условию
b=a+2
периметр p считается:
2*a+2*b=p
подставляем b:

2*a+2*(a+2)=p
раскрываем скобки
4*a+4=p

отсюда находим a
a= (p-4)/4
а следом и b=a+2

вроде так..

Источник

Сторона параллелограмма

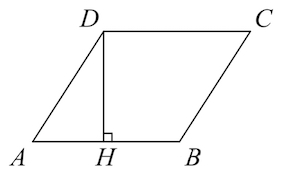
Зная диагонали параллелограмма и одну его сторону, можно найти вторую сторону. Для этого нужно извлечь квадратный корень из половины суммы квадратов диагоналей без удвоенного квадрата известной стороны.

Другой способ как вычислить сторону параллелограмма требует высоты и противолежащего ей угла, тогда из прямоугольного треугольника, образованного высотой, сторона параллелограмма будет равна отношению высоты к синусу известного угла:

Также высоту можно использовать при нахождении стороны параллелограмма через площадь. Так как площадь параллелограмма представляет собой произведение стороны и высоты, то сторона будет отношением площади к высоте, которая падает на эту сторону:

Геометрические фигуры. Параллелограмм. Стороны, диагонали параллелограмма.

Формулы для вычисления длин сторон параллелограмма:

1. Формула сторон параллелограмма через диагонали и угол между ними:

2. Формула сторон параллелограмма через диагонали и вторую сторону:

3. Формула сторон параллелограмма через высоту и sin угла:

4. Формула сторон параллелограмма через площадь и высоту:

Диагонали параллелограмма.

Диагональю параллелограмма является каждый отрезок соединяющий 2 вершины противолежащих углов параллелограмма.

У параллелограмма есть 2 диагонали — длинная d₁, и короткая — d₂

Формулы вычисления длины диагонали параллелограмма:

1. Формулы диагоналей параллелограмма через стороны и cos β (из теоремы косинусов):

2. Формулы диагоналей параллелограмма через стороны и cos α (из теоремы косинусов):

3. Формула диагонали параллелограмма через 2 стороны и известную вторую диагональ:

4. Формула диагонали параллелограмма через площадь, диагональ которая известна, и угол между диагоналями:

Как найти большую сторону параллелограмма

Тип 3 № 49979

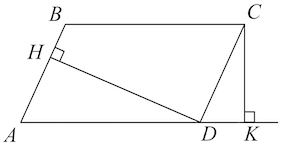
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.

Это задание ещё не решено, приводим решение прототипа.

Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Заметим, что как накрест лежащие углы при пересечении параллельных прямых секущей. Значит, треугольник ADL − равнобедренный. Пусть тогда Противоположные стороны параллелограмма ABCD попарно равны, тогда

Источник

Задания

Версия для печати и копирования в MS Word

Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 2 : 7, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.

Решение.

Это задание ещё не решено, приводим решение прототипа.

Заметим, что как накрест лежащие углы при пересечении параллельных прямых секущей. Значит, треугольник ADL − равнобедренный. Пусть AL=4x, тогда AD=4x, AB=7x. Противоположные стороны параллелограмма ABCD попарно равны, тогда

откуда x=4. Находим

Ответ: 28.

Кодификатор ФИПИ/Решу ЕГЭ:

Источник

Бонифат

15 октября, 20:05

Диомид

15 октября, 21:32

0

Меньшая сторона х, большая сторона 6 х.

Р = (х+6 х) * 2=126

7 х=126:2=63

х=9 см – (меньшая сторона)

Большая сторона=9*6=54 см

Так наверное)
- Комментировать
- Жалоба
- Ссылка

Найди верный ответ на вопрос ✅ «Даны длины двух сторон параллелограмма относятся как 1:6 а его периметр равен 126. Найти большую сторону параллелограмма …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Новые вопросы по геометрии

Главная » Геометрия » Даны длины двух сторон параллелограмма относятся как 1:6 а его периметр равен 126. Найти большую сторону параллелограмма

Источник

24
Июл 2013

Категория: 01 Геометрия

01. Параллелограмм

2013-07-24
2022-09-11

Задача 1. Сумма двух углов параллелограмма равна $62^{circ}$ . Найдите один из оставшихся углов. Ответ дайте в градусах.

Решение: + показать

Задача 2. Один угол параллелограмма больше другого на $70^{circ}$ . Найдите больший угол. Ответ дайте в градусах.

Решение: + показать

Задача 3. Найдите больший угол параллелограмма, если два его угла относятся как Ответ дайте в градусах.

Решение: + показать

Задача 4. Диагональ параллелограмма образует с двумя его сторонами углы $5^{circ}$ и $38^{circ}.$ Найдите больший угол параллелограмма. Ответ дайте в градусах.

Решение: + показать

Задача 5. Периметр параллелограмма равен Меньшая сторона равна Найдите большую сторону параллелограмма.

Решение: + показать

Задача 6. Две стороны параллелограмма относятся как а периметр его равен Найдите большую сторону параллелограмма.

Решение: + показать

Задача 7. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна Найдите его большую сторону.

Решение: + показать

Задача 8. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.

Решение: + показать

Задача 9. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен

Решение: + показать

Задача 10. В параллелограмме высота, опущенная на сторону из точки равна . Найдите синус угла .

Решение: + показать

Задача 11. В параллелограмме $sinC=frac{5}{7},;AD=7.$ Найдите высоту, опущенную на сторону

Решение: + показать

Задача 12. В параллелограмме $AB=6,;AD=14,;sinA=frac{6}{7}.$ Найдите большую высоту параллелограмма.

Решение: + показать

Задача 13. Площадь параллелограмма равна две его стороны равны и Найдите большую высоту этого параллелограмма.

Решение: + показать

Задача 14. В параллелограмме $sinA=frac{sqrt{561}}{25}$ . Найдите .

Решение: + показать

Задача 15. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Решение: + показать

Задача 16. Площадь параллелограмма равна Точка — середина стороны . Найдите площадь трапеции .

Решение: + показать

Задача 17. Площадь параллелограмма равна Найдите площадь параллелограмма вершинами которого являются середины сторон данного параллелограмма.

Решение: + показать

Задача 18. Найдите диагональ параллелограмма , если стороны квадратных клеток равны 1.

Решение: + показать

Задача 19. Диагонали четырехугольника равны и Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.