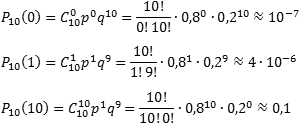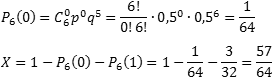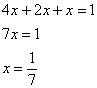Как найти бракованную деталь

Решение задач про выбор деталей

Общая постановка задачи примерно* следующая:

В ящике находится $K$ стандартных и $N-K$ бракованных деталей (всего $N$ деталей). Наудачу и без возвращения вынимают $n$ деталей. Найти вероятность того, что будет выбрано ровно $k$ стандартных и $n-k$ бракованных деталей.

*Поясню, что значит “примерно”: вместо деталей могут фигурировать изделия, болты, телевизоры и т.п.; детали могут быть стандартными и бракованными, или годными и дефектными, или обычными и поломанными и так далее. Главное, чтобы они были ДВУХ типов, тогда один тип вы считаете условно “стандартными”, второй – “бракованными” и используете формулу для решения, которую мы выведем ниже.

Сначала найдем общее число исходов – это число всех различных способов выбрать любые $n$ деталей из общего множества в $N$ деталей (без учета порядка), то есть число сочетаний $C_N^n$ (см. подробнее про сочетания).

Теперь найдем число всех способов выбрать $k$ стандартных деталей из $K$ возможных – это сочетания $C_K^k$, и одновременно число всех способов выбрать $n-k$ бракованных деталей из $N-K$ возможных – $C_{N-K}^{n-k}$. По правилу произведения перемножая эти числа, получим число исходов, благоприятствующих нашему событию – $C_K^k cdot C_{N-K}^{n-k}$.

Применяя классическое определение вероятности – поделив число благоприятствующих исходов на общее число исходов, придем к искомой формуле:

$$
P=frac{C_K^k cdot C_{N-K}^{n-k}}{C_N^n}. qquad (1)
$$

Видеоурок и шаблон Excel

Посмотрите наш ролик о решении задач про детали в схеме гипергеометрической вероятности, узнайте, как использовать Excel для решения типовых задач.

Расчетный файл Эксель из видео можно бесплатно скачать и использовать для решения своих задач.

Примеры решений задач о выборе деталей/изделий

Пример 1. В партии из 12 изделий 5 изделий имеют скрытый дефект. Какова вероятность того, что из взятых наугад 4 изделий 2 изделия являются дефектными?

Популярная задача из методички, в которой меняются только цифры, а вариантов множество. С помощью данного решения и калькулятора ниже для числовых расчетов, вы легко получите полное решение задачи. Для разнообразия сделаем подробное пояснение.

Начинаем решение задачи с ввода события $A = $ (Из взятых наугад 4 изделий 2 изделия являются дефектными) и общей формулы для нахождения вероятности. Так как речь идет о выборе объектов из совокупности, используем классическое определение вероятности $P(A)=m/n$, где $n$ – общее число всех равновозможных элементарных исходов, а $m$ – число исходов, благоприятствующих событию $A$.

Сначала найдем общее число исходов – это число способов выбрать любые 4 изделия из партии в 12 изделий. Так как порядок выбора несущественнен, применяем формулу для числа сочетаний из 12 объектов по 4: $n=C_{12}^4$.

Теперь переходим к числу благоприятствующих событию исходов. Для этого нужно, чтобы из 4 выбранных изделий 2 были дефектные (выбираем любые 2 дефектные изделия из 5 $C_5^2$ способами) и еще 2 – стандартные (выбираем любые 2 стандартные изделия из 12-5=7 имеющихся в партии $C_7^2$ способами). Тогда всего способов выбрать 2 дефектных и 2 обычных изделия из партии будет $m = C_5^2 cdot C_7^2$.

Нужная вероятность равна:

$$
P(A)=frac{m}{n}=frac{C_{5}^2 cdot C_{7}^{2}}{C_{12}^4} = frac{10 cdot 21}{495} = 0.424.
$$

Пример 2. В ящике 16 стандартных и 7 бракованных деталей. Наудачу извлечены 6 деталей. Найти вероятность того, что среди извлеченных ровно 4 стандартных детали.

Подставляем в формулу (1) значения: $K=16$ стандартных деталей, $N-K=7$ бракованных деталей, итого $N=16+7=23$ всего деталей в ящике. Из ящика извлекают $n=6$ деталей, из них должно быть $k=4$ стандартных и соответственно, $n-k=6-4=2$ бракованные. Получаем нужную вероятность:

$$
P=frac{C_{16}^4 cdot C_{7}^{2}}{C_{23}^6} = frac{1820 cdot 21}{100947} = 0.379.
$$

Пример 3. В партии из 12 изделий 8 стандартных. Найти вероятность того, что среди 3 наугад взятых есть хотя бы одно нестандартное.

Эта задача самую малость сложнее предыдущих. В ней помимо исходного события
$A = $ (Среди 3 наугад взятых изделий есть хотя бы одно нестандартное),
введем еще противоположное ему событие, которое можно записать как
$overline{A} = $ (Все три выбранные изделия стандартные).

Будем искать вероятность события $overline{A}$. Выпишем значения параметров: $K=8$ стандартных изделия, $N-K=12-8=4$ нестандартных изделия, всего $N=12$ изделий в партии. Из партии извлекают $n=3$ изделия, и все они должны оказаться стандартными, то есть $k=3$ и $n-k=0$.

$$
P(overline{A})=frac{C_{8}^3 cdot C_{4}^{0}}{C_{12}^3} = frac{56 cdot 1}{220}= frac{14}{55} = 0.255.
$$

Тогда вероятность искомого события (что будет хотя бы одно нестандартное изделие из 3), равна:

$$
P(A)= 1 – P(overline{A})= 1- 0.255 = 0.745.
$$

Пример 4. Мастер для замены получил 8 однотипных деталей, из которых 3 бракованные. Он заменил 2 детали. Найти вероятность того, что замененными оказались годные детали.

Подставляем в формулу (1) значения: $K=8-3=5$ годных деталей, $N-K=3$ бракованных, $N=8$ всего деталей у мастера. Выбираем для замены $n=2$ детали, и обе они должны оказаться годными, то есть: $k=2$, $n-k=0$. Приходим к ответу:

$$
P=frac{C_{5}^2 cdot C_{3}^{0}}{C_{8}^2} = frac{10 cdot 1}{28} = frac{5}{14} = 0.357.
$$

Полезные ссылки

• Онлайн учебник по теории вероятностей
• Еще примеры решений задач по теории вероятностей
• Заказать решение теории вероятностей

Поищите готовые задачи в решебнике:

Схема Бернулли. Примеры решения задач

5 июля 2011

Не будем долго размышлять о высоком — начнем сразу с определения.

Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.

Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы.

Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:

1. A — появление события A с вероятностью p;
2. «не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.

Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p.

Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Об этом вам расскажет любой грамотный репетитор по высшей математике. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности.

Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:

Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:

где C_n^k — число сочетаний, q = 1 − p.

Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.

Задача. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.

По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A», т.е. выпуск бракованного изделия.

Таким образом, имеем: n = 10; p = 0,8; q = 0,2.

Итак, находим вероятность того, что в партии все детали бракованные (k = 0), что только одна деталь без брака (k = 1), и что бракованных деталей нет вообще (k = 10):

Задача. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что:

1. герб выпадет три раза;
2. герб выпадет один раз;
3. герб выпадет не менее двух раз.

Итак, нас интересует событие A, когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A», когда выпадает решка, что случается с вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадет k раз.

Таким образом, имеем: n = 6; p = 0,5; q = 0,5.

Определим вероятность того, что герб выпал три раза, т.е. k = 3:

Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1:

Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k, кроме 0 и 1, т.е. надо найти значение суммы X = P₆(2) + P₆(3) + … + P₆(6).

Заметим, что эта сумма также равна (1 − P₆(0) − P₆(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз (k = 1) или не выпал вообще (k = 0). Поскольку P₆(1) нам уже известно, осталось найти P₆(0):

Задача. Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?

Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8.

Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8.

Найдем вероятность получить два «дефектных» телевизора (k = 2) и три (k = 3):

[begin{array}{l}{P_{20}}left( 2 right) = C_{20}^2{p^2}{q^{18}} = frac{{20!}}{{2!18!}} cdot {0,2^2} cdot {0,8^{18}} approx 0,137\{P_{20}}left( 3 right) = C_{20}^3{p^3}{q^{17}} = frac{{20!}}{{3!17!}} cdot {0,2^3} cdot {0,8^{17}} approx 0,41end{array}]

Очевидно, P₂₀(3) > P₂₀(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая.

Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению.

P. S. А самая большая вероятность в последней задаче — это получить четыре телевизора со скрытыми дефектами. Подсчитайте сами — и убедитесь.

Смотрите также:

1. Локальная теорема Муавра — Лапласа
2. Формула полной вероятности
3. Тест к уроку «Сложение и вычитание дробей» (легкий)
4. Сводный тест по задачам B12 (2 вариант)
5. Как решать задачи про летающие камни?
6. Задача C1: тригонометрические уравнения и формула двойного угла



Материал тесно связан с содержанием предыдущего параграфа. Пусть событие  наступило в результате осуществления одной из гипотез .  Как определить вероятность того, что имела

место та или иная гипотеза?

При условии, что событие  уже произошло, вероятности гипотез переоцениваются по

формулам, которые в своё время предложил английский священник Томас Байес:
 – вероятность того, что имела

место гипотеза ;
 – вероятность того, что имела

место гипотеза ;
 – вероятность того, что имела

место гипотеза ;
…
 – вероятность того, что имела место

гипотеза .

На первый взгляд кажется полной нелепицей – зачем пересчитывать вероятности гипотез, если они и так известны? Но на самом деле разница

есть:

 – это априорные (оцененные

до испытания) вероятности.

 – это апостериорные (оцененные

после испытания) вероятности тех же гипотез, пересчитанные в связи «со вновь открывшимися обстоятельствами » – с учётом

того факта, что событие  достоверно произошло.

Рассмотрим это различие на конкретном примере:

Задача 60
На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии

составляет 20%, а во второй – 10%. Наудачу взятое со склада изделие оказалось стандартным. Найти вероятность того, что оно: а) из первой

партии, б) из второй партии.

Первая часть решения состоит в использовании формулы полной вероятности.

Иными словами, вычисления проводятся в предположении, что испытание ещё не произведено и событие «изделие оказалось

стандартным» пока не наступило.

Рассмотрим две гипотезы:
 – наудачу взятое изделие будет из

1-й партии;
 – наудачу взятое изделие будет

из 2-й партии.

Всего: 4000 + 6000 = 10000 изделий на складе. По классическому определению:
.

Контроль:  

Рассмотрим зависимое событие:  –

наудачу взятое со склада изделие будет стандартным.

В первой партии 100% – 20% = 80% стандартных изделий, поэтому:  – вероятность того, что наудачу взятое на складе изделие будет стандартным

при условии, что оно принадлежит 1-й партии.

Аналогично, во второй партии 100% – 10% = 90% стандартных изделий и  – вероятность того, что наудачу взятое на складе изделие будет стандартным

при условии, что оно принадлежит 2-й партии.

По формуле полной вероятности:
 – вероятность того, что наудачу

взятое на складе изделие будет стандартным.

Часть вторая. Пусть наудачу взятое со склада изделие оказалось стандартным. Эта фраза прямо прописана в условии, и она

констатирует тот факт, что событие  произошло. По формулам Байеса:

а)  – вероятность того, что выбранное

стандартное изделие принадлежит 1-й партии;

б)  – вероятность того, что выбранное

стандартное изделие принадлежит 2-й партии.

После переоценки гипотезы ,

разумеется, по-прежнему образуют полную группу:
 (проверка ;-))

Ответ:

Понять смысл переоценки гипотез нам поможет Иван Васильевич, которой снова сменил профессию и стал директором завода. Он знает, что

сегодня 1-й цех отгрузил на склад 4000, а 2-й цех – 6000 изделий, и приходит удостовериться в этом. Предположим, вся продукция однотипна и

находится в одном контейнере. Естественно, Иван Васильевич подсчитал, что изделие, которое он сейчас извлечёт для проверки, с вероятностью

 выпущено первым цехом и с вероятностью

 – вторым.

Но после того как выбранное изделие оказывается стандартным, он восклицает: «Какой же классный болт! – его скорее выпустил 2-й цех».

Таким образом, вероятность второй гипотезы переоценивается в лучшую сторону , а вероятность первой гипотезы занижается: . И эта переоценка небезосновательна – ведь 2-й цех произвёл не только больше

изделий, но и работает в 2 раза лучше!

Вы скажете, чистый субъективизм? Отчасти – да, более того, сам Байес интерпретировал апостериорные вероятности как

уровень доверия.

И, несмотря на то, что у байесовского подхода немало критиков, в нём есть и объективное зерно. Ведь вероятности того, что изделие

будет стандартным (0,8 и 0,9 для 1-го и 2-го цехов соответственно) это предварительные (априорные) и

средние оценки.

Но, выражаясь философски – всё течёт, всё меняется, и вероятности в том числе. Вполне возможно, что на момент

исследования более успешный 2-й цех повысил процент выпуска стандартных изделий (и / или 1-й цех снизил), и если

проверить бОльшее количество либо все 10 тысяч изделий на складе, то переоцененные значения  окажутся гораздо ближе к истине.

Кстати, если Иван Васильевич извлечёт нестандартную деталь, то наоборот – он будет больше «подозревать» первый цех и меньше – второй.

Предлагаю убедиться в этом самостоятельно:

Задача 61
На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии 20%,

во второй – 10%. Наудачу взятое со склада изделие оказалось нестандартным. Найти вероятность того, что оно: а) из первой

партии, б) из второй партии.

Условие отличатся двумя буквами, которые я выделил жирным шрифтом. Задачу можно решить с «чистого листа», или воспользоваться

результатами предыдущих вычислений. В образце я провёл полное решение, но чтобы не возникло формальной накладки с предыдущей задачей,

событие «наудачу взятое со склада изделие будет нестандартным» обозначено через .

Байесовская схема переоценки вероятностей встречается повсеместно, причём её активно эксплуатируют и различного рода мошенники.

Рассмотрим ставшее нарицательным АО на три буквы, которое привлекает вклады населения, якобы куда-то их инвестирует, исправно выплачивает

2% в день и т.д. Что происходит? Проходит день за днём, месяц за месяцем и всё новые и новые факты, донесённые путём рекламы и «сарафанным

радио», только повышают уровень доверия к финансовой пирамиде (апостериорная байесовская переоценка в связи с произошедшими

событиями!). То есть, в глазах вкладчиков происходит постоянное увеличение вероятности того, что «это серьёзная контора»; при

этом вероятность противоположной гипотезы («это очередной лохотрон»), само собой, уменьшается и уменьшается. Дальнейшее, думаю,

понятно. Примечательно, что заработанная репутация даёт организаторам время успешно скрыться от Ивана Васильевича, который остался не

только без партии болтов, но и без штанов.

К не менее любопытным примерам мы вернёмся чуть позже, а пока на очереди, пожалуй, самый распространенный случай с тремя гипотезами: 

Задача 62
Электролампы изготавливаются на трех заводах. 1-ый завод производит 30% общего количества ламп, 2-й – 55%, а 3-й – остальную часть.

Продукция 1-го завода содержит 1% бракованных ламп, 2-го – 1,5%, 3-го – 2%. В магазин поступает продукция всех трех заводов. Купленная

лампа оказалась с браком. Какова вероятность того, что она произведена 2-м заводом?

Заметьте, что в задачах на формулы Байеса в условии обязательно фигурирует некое произошедшее событие, в данном случае

– покупка лампы.

Событий прибавилось, и решение удобнее оформить в «быстром» стиле.

Алгоритм точно такой же: на первом шаге находим вероятность того, что купленная лампа вообще окажется

бракованной.

Пользуясь исходными данными, переводим проценты в вероятности:
 – вероятности того, что лампа

произведена 1-м, 2-м и 3-м заводами соответственно.

Контроль:
Аналогично:
 – вероятности изготовления бракованной

лампы для соответствующих заводов.

По формуле полной вероятности:

 – вероятность того, что купленная

лампа окажется с браком.

Шаг второй. Пусть купленная лампа оказалась бракованной (событие произошло)

По формуле Байеса:
 – вероятность того, что купленная

бракованная лампа изготовлена вторым заводом

Ответ:  – отвечаем

только на то, о чём спрашивалось в условии!

Почему изначальная вероятность 2-й гипотезы  после переоценки увеличилась ? Ведь второй завод производит «средние» по качеству лампы (первый – лучше,

третий – хуже). Так почему же возросла апостериорная вероятность, что бракованная лампа именно со 2-го завода? Это объясняется уже

не «репутацией», а размером. Так как завод № 2 выпустил самое большое количество ламп (более половины), то логично субъективное завышение

оценки по принципу «скорее всего, эта бракованная лампа именно оттуда».

Интересно заметить, что вероятности 1-й и 3-й гипотез, переоценились в ожидаемых направлениях и сравнялись:

Контроль: , что и требовалось

проверить.

К слову, о заниженных и завышенных оценках:

Задача 63
В студенческой группе 3 человека имеют высокий уровень подготовки, 19 человек – средний и 3 – низкий. Вероятности успешной сдачи

экзамена для данных студентов соответственно равны: 0,95; 0,7 и 0,4. Известно, что некоторый студент сдал экзамен. Какова вероятность того,

что:

а) он был подготовлен очень хорошо;
б) был подготовлен средне;
в) был подготовлен плохо.

Проведите вычисления и проанализируйте результаты переоценки гипотез.
Предложенная задача приближена к реальности и особенно правдоподобна для группы студентов-заочников, где преподаватель практически не

знает способностей того или иного студента. При этом результат может послужить причиной довольно-таки неожиданных последствий (особенно

это касается экзаменов в 1-м семестре). Если плохо подготовленному студенту посчастливилось с билетом, то преподаватель с большой

вероятностью сочтёт его хорошо успевающим или даже сильным студентом, что принесёт неплохие дивиденды в будущем (естественно, нужно

«поднимать планку» и поддерживать свой имидж). Если же студент 7 дней и 7 ночей учил, «зубрил», повторял, но ему просто не повезло, то

дальнейшие события могут развиваться в самом скверном ключе – с многочисленными пересдачами и балансировкой на грани «вылета».

Что и говорить, репутация – это важнейший капитал, не случайно многие корпорации носят имена-фамилии своих отцов-основателей, которые

руководили делом 100-200 лет назад и прославились своей безупречной репутацией.

Да, байесовский подход в известной степени субъективен, но… так устроена жизнь!

Решение: в отличие от предыдущих задач здесь в явном виде задан вопрос, который разрешается с помощью формулы полной

вероятности. Но с другой стороны, условие немного «зашифровано», и разгадать этот ребус нам поможет школьный навык составлять простейшие

уравнения. За «икс» удобно принять наименьшее значение:

Пусть  – доля деталей, выпускаемая

третьим цехом.

По условию, первый цех производит в 4 раза больше третьего цеха, поэтому доля 1-го цеха составляет . Кроме того, первый цех производит изделий в 2 раза больше, чем

второй цех, а значит, доля последнего: .

Составим и решим уравнение:

Таким образом:  – вероятности того,

что извлечённая из контейнера деталь выпущена 1-м, 2-м и 3-м цехами соответственно.

Контроль: . Кроме того, будет не лишним

ещё раз посмотреть на фразу «Известно, что первый цех производит изделий в 2 раза больше второго цеха и в 4 раза больше третьего

цеха» и убедиться, что полученные значения вероятностей действительно соответствуют этому условию.

За «икс» изначально можно было принять долю 1-го либо долю 2-го цеха – вероятности выйдёт такими же. Но, так или иначе, самый трудный

участок пройден, и решение входит в накатанную колею:

Из условия находим:
 – вероятности изготовления

бракованной детали для соответствующих цехов.

По формуле полной вероятности:

 – вероятность того, что наугад

извлеченная из контейнера деталь окажется нестандартной.

Вопрос второй: какова вероятность того, что извлечённую бракованную деталь выпустил 3-й цех? Данный вопрос

предполагает, что деталь уже извлечена, и она оказалось бракованной. Переоцениваем гипотезу по формуле Байеса:
 – искомая вероятность. Совершенно

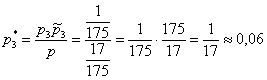
ожидаемо – ведь третий цех производит не только самую малую долю деталей, но и лидирует по качеству!

Коль скоро в условии нет пунктов «а» и «бэ», то ответ лучше снабдить текстовыми комментариями:

Ответ:  – вероятность

того, что извлечённая из контейнера деталь окажется бракованной;  – вероятность того, что извлечённую бракованную деталь выпустил 3-й цех.

Как видите, задачи на формулу полной вероятности и формулы Байеса достаточно простЫ, и, наверное, по этой причине в них так часто

пытаются затруднить условие, о чём я уже упоминал в начале параграфа.

1.9. Независимые испытания и формула Бернулли

1.7. Формула полной вероятности

| Оглавление |



Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Как определить бракованные автозапчасти на рынке

Практически каждому автомобилю рано или поздно требуется замена каких-либо запчастей. Можно обратиться к официальному дилеру, но тогда придется переплачивать. Это нецелесообразно, если вы владеете автомобилем среднего класса, а гарантийный срок давно уже истек. Более экономный вариант – пойти на рынок, чтобы приобрести все необходимое. Однако нужно уметь отличать бракованные детали.

Вам понадобится

• – запчасти;
• – сертификат качества;
• – упаковка товара;
• – деньги.

Инструкция

Осмотрите внимательно каждую покупаемую деталь. Будьте осторожны! На авторынках очень часто продают восстановленные запчасти. Их можно отличить по потертостям и отсутствию упаковки. Оторванные ярлычки или наклейки с датой изготовления могут свидетельствовать о том, что товар был ранее в употреблении, а продавец хочет скрыть этот факт. Ни в коем случае не покупайте запчасти с рук! Нередко подержанные детали становятся причиной крупной поломки или страшной аварии.

Возьмите с собой знающего человека, если вы плохо разбираетесь в автомобильных запчастях. Наверняка среди ваших знакомых или родственников найдутся сведущие в данном вопросе люди. Поняв, чтобы плохо разбираетесь в автомобильных запчастях, недобросовестный продавец постарается продать вам бракованную или испорченную запчасть.

Попросите продавца предъявить сертификат качества. Оригинальные и сертифицированные запчасти обязательно имеют такой сертификат. Внимательно изучите предъявленный документ. В нем должна быть указана исчерпывающая информация о продукции. Обратите внимание на наличие печатей. Если такой бумаги у продавца нет или она вызывает подозрение, то следует воздержаться от совершения покупок в этом магазине.

Обращайте внимание на условия хранения продукции. Масла и другие жидкости не должны находиться на улице, ведь под воздействием мороза и прямых лучей солнца химический состав начинает меняться и терять свои изначальные свойства. Не покупайте детали, сваленные в одну общую кучу. Каждая настоящая запчасть имеет свою собственную коробочку, а также специальную полиэтиленовую прокладку, которая защищает от механических повреждений при транспортировке.

Не покупайте свежевыкрашенные детали. Свежая краска указывает на то, что товар красили прямо перед продажей, чтобы скрыть следы использования. Всегда берите чек. Это позволит вам требовать замены детали в том случае, если она не подойдет вам или окажется ненадлежащего качества. Обращайте внимание на чек. Он должен быть распечатан на специальном кассовом аппарате с указанием даты и времени совершения покупки, наименования товара, цены, фамилии и имени продавца. При необходимости требуйте у продавца товарный чек.

Лучше всего покупать на рынке те детали, которые никак не влияют на техническое состояние автомобиля. В таком случае нет риска, что купленная деталь станет причиной аварии или поломки, зато вы сэкономите деньги, ведь в магазине или у официального дилера эти же самые запчасти продаются в разы дороже.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?